氢分子间色散相互作用能的自然轨道泛函
2022-03-04盛晓伟
盛晓伟
(安徽师范大学 物理与电子信息学院, 芜湖 241000)
1 引 言
色散相互作用源于电子间的非定域关联效应,它是原子分子间多种相互作用中的一种. 由于其在气液相变、液固相变以及冷原子碰撞等重要物理过程中起关键性的作用[1-3],从而引起了人们的广泛关注. 目前对色散相互作用能的理论计算主要有以下三种方法:半经验的势模型法、电子相关的从头计算法以及密度泛函法. 在半经验势模型方法中,体系的色散相互作用能一般用一个包含若干参数的解析式进行表示. 然而势模型中参数值的确定,依赖于实验或者精确的从头计算[4,5],因此势模型方法在实际应用中受到一定的限制;电子相关的从头计算方法可以很精确地计算出色散相互作用能,并且不依赖于任何参数[6,7]. 然而这类方法的计算量随体系的增大而快速增长,很难推广到大分子体系[8];密度泛函理论在处理色散相互作用问题上,一直没有得到很好的解决. 基于局域密度和广义梯度密度近似的密度泛函,无法描述具有非定域性质的色散相互作用[9]. 近些年有很多设法计算色散相互作用能的半经验密度泛函相继被报道[10-14],然而随着密度泛函对色散相互作用能计算精度的增加,泛函的形式越来越复杂,计算量也越来越大[15]. Baerends 等[16]在文章中指出:“截止目前,无法构造出一个能够精确处理色散相互作用能的简单密度泛函”. 可见,发展一种能够对原子分子间色散相互作用实现高效计算的理论方法仍然是个有待解决的基础科学问题.
密度矩阵泛函以非定域量一阶密度矩阵为基本变量(一阶密度矩阵可以利用其本征函数自然轨道和本征值自然轨道占居数展开,因此密度矩阵泛函也称为自然轨道和自然轨道占居数泛函),在计算量上与密度泛函接近,例如:Buijse-Baerends(BB)泛函的计算量按基组的4次方增长,这和一般密度泛函的计算量相当[17]. 密度矩阵泛函和密度泛函的最大区别在于:体系的动能可以用一阶密度矩阵进行精确表示,无需构造Kohn-Sham无相互作用体系,这使其在处理电子相关问题上较密度泛函更具有优势. 如:BB泛函成功地描述了一些小分子体系中的电荷转移以及化学键的离解过程[18];Sharma的幂函数能够正确计算出半导体以及过渡金属氧化物绝缘体的帯隙[19];最近该泛函又被成功的运用到同性电子气和一维以及二维异性Hubbard模型中[20-22].
密度矩阵与色散相互作用都具有非定域的性质. 因此,利用密度矩阵泛函对原子间色散相互作用进行计算引起了广泛的关注. Cioslowski和Pernal[23]基于对两个弱相互作用体系总能量渐进形式的研究以及自旋轨道在两个体系中具有完全定域性质的假设,得到了描述色散相互作用能的密度矩阵泛函所必须满足的条件,但其并没有给出该密度矩阵泛函的具体形式. Gritsenko和Baerends[24]通过分析自然轨道和自然轨道占据数表象下双电子体系的三重态波函数,得到了三态氢分子在范德瓦尔斯势阱位置附近的势能曲线. 研究结果表明:该体系中的色散相互作用能在自然轨道表象下收敛速度非常快. 10个自然轨道组合成的组态波函数已经能够计算出体系 90% 以上的色散相互作用能,然而在Kohn-Sham和Hartree-Fock轨道基组下,得到同样比例的色散相互作用能却都需要60个以上轨道. 由此可见:自然轨道相较于Kohn-Sham轨道和Hartree-Fock轨道更适合描述色散相互作用,密度矩阵泛函较密度泛函在处理色散相互作用上更具有优势. 2007年,Piris等[25]提出了一个完全由交换和库仑积分构成的密度矩阵泛函(PNOF2). 该泛函能够给出基态 He2的势阱位置Re,但只能得到50%的势阱深度De. 2013年,本课题组分析了基态 H2和 He2的对关联函数,基于色散相互作用的非定域特性,首次辨认出对关联函数中描述色散相互作用的项,在此基础上找到了基态H2和He2的色散相互作用能自然轨道泛函[26]. 本文将在此基础上进一步分析两相互平行的氢分子间色散相互作用能的自然轨道泛函形式.
2 两相互平行的氢分子间色散相互作用能
两相互平行的氢分子体系属于 D2h群, 该群有8种不可约表示:ag,b3u,b1g,b2u,b2g,b1u,b3g和au. 图1展示了该体系的几何结构.
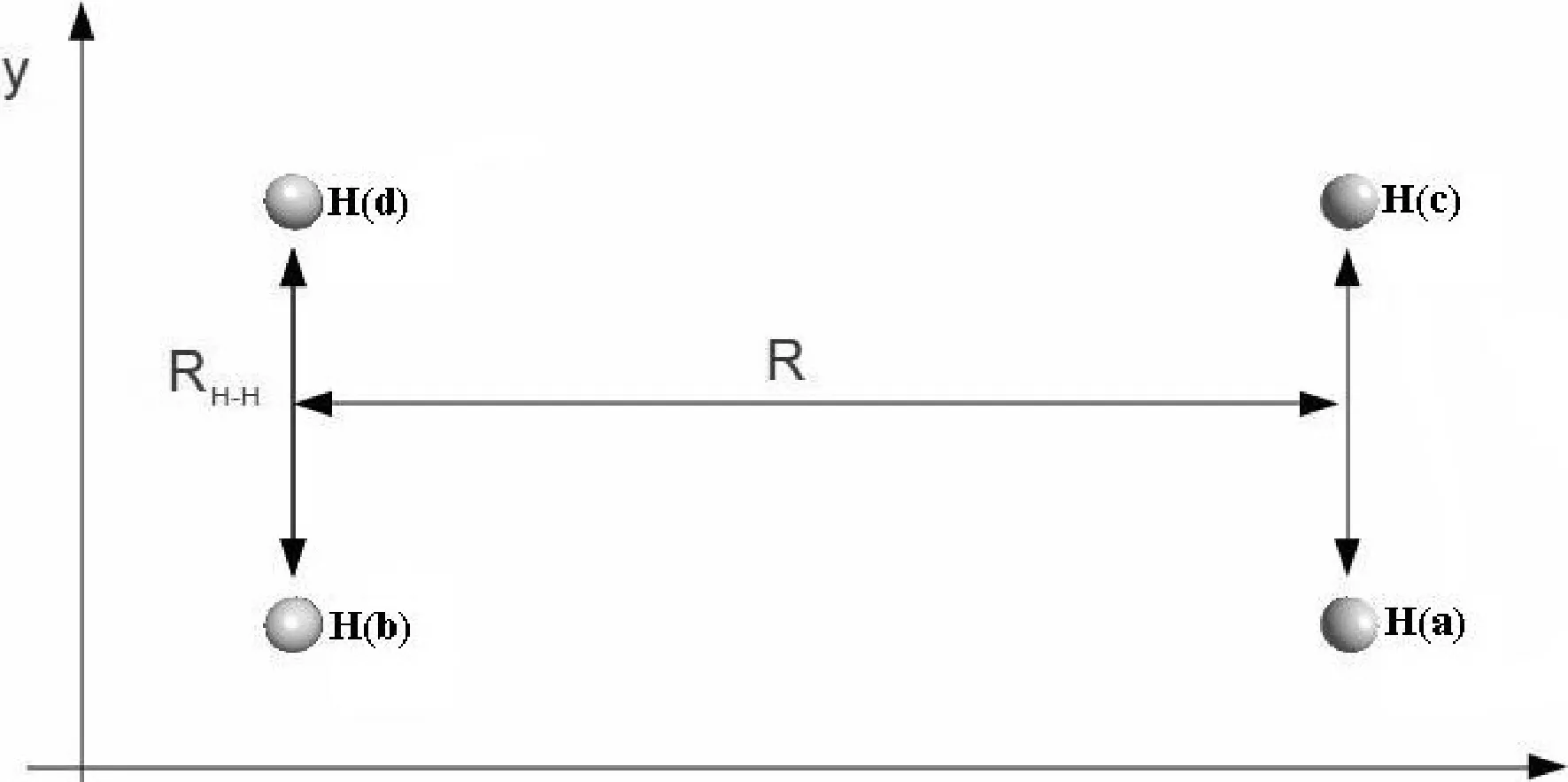
图1 两相互平行的氢分子结构图Fig. 1 The geometry of two parallel hydrogen molecules
该体系的基态行列式为ag,b3u两分子轨道双占据,即:
Ψ0=|lagαlagβlb3uαlb3uβ|
(1)
前期研究工作指出, 体系的色散相互作用能可通过计算一些特定双重激发组态所贡献的电子间相互作用能而得到. 对于基态 He2分子,我们发现E类双重激发组态为该体系色散相互作用能的主要贡献项[16]. 本文的研究体系与He2分子具有类似的双重激发组态. 因此,E类双重激发组态在两相互平行的氢分子体系中必然也是其色散相互作用能的主要贡献项. 该体系中E类双重激发组态为如下四种组合形式:
(2)
电子间相互作用能计算公式如下:
(3)
Γ(1,2)为二阶密度矩阵,其定义如下:
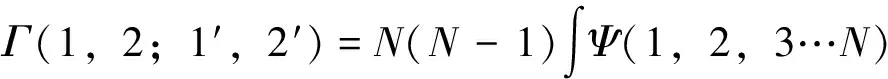
Ψ*(1′,2′,3…N)d3…dN
(4)
其中Ψ(1,2,3…N)为该体系的组态波函数,为了得到E类激发组态所贡献的电子间相互作用能,我们考虑ΨE(a,b,c,d)激发组态和Ψ0的乘积对二阶密度矩阵的贡献. 现以ΨE(a)为例来作此分析,
(5)
ΨE(a)所包含的6个行列式与Ψ0均只有两个轨道不同,利用Slater-Condon规则可计算得到ΨE(a)与Ψ0乘积所得到如下的六个二阶密度矩阵:
[mag(1)nb3u(2)lag(1′)lb3u(2′)-
mag(1)nb3u(2)lb3u(1′)lag(2′)-
nb3u(1)mag(2)lag(1′)lb3u(2′)-
nb3u(1)mag(2)lb3u(1′)lag(2′)]ββββ
(6)
[mag(1)nb3u(2)lag(1′)lb3u(2′)-
mag(1)nb3u(2)lb3u(1′)lag(2′)-
nb3u(1)mag(2)lag(1′)lb3u(2′)+
nb3u(1)mag(2)lb3u(1′)lag(2′)]αααα
(7)
[mag(1)αnb3u(2)βlag(1′)βlb3u(2′)α-
mag(1)αnb3u(2)βlb3u(1′)αlag(2′)β-
nb3u(1)βmag(2)αlag(1′)βlb3u(2′)α+
nb3u(1)βmag(2)αlb3u(1′)αlag(2′)β]
(8)
[mag(1)βnb3u(2)αlag(1′)βlb3u(2′)α-
mag(1)βnb3u(2)αlb3u(1′)αlag(2′)β-
nb3u(1)αmag(2)βlag(1′)βlb3u(2′)α+
nb3u(1)αmag(2)βlb3u(1′)αlag(2′)β]
(9)
[mag(1)αnb3u(2)βlag(1′)αlb3u(2′)β-
mag(1)αnb3u(2)βlb3u(1′)βlag(2′)α-
nb3u(1)βmag(2)αlag(1′)αlb3u(2′)β+
nb3u(1)βmag(2)αlb3u(1′)βlag(2′)α]
(10)
[mag(1)βnb3u(2)αlag(1′)αlb3u(2′)β-
mag(1)βnb3u(2)αlb3u(1′)βlag(2′)α-
nb3u(1)αmag(2)βlag(1′)αlb3u(2′)β+
nb3u(1)αmag(2)βlb3u(1′)βlag(2′)α]
(11)
将式(6-11)代入到式(3),得E(a)类激发组态所贡献的电子间相互作用能,其具体形式如下:
〈1ag1b3u|nb3umag〉]
(12)
同理可得E(b),E(c) 和E(d)类激发组态所贡献的电子间色散相互作用能.
〈1ag1b3u|nb2umb1g〉]
(13)
〈1ag1b3u|nb1umb2g〉]
(14)
〈1ag1b3u|naumb3g〉]
(15)
通过分析式(12-15)可知:色散相互作用能来源于自旋相同部分正好是自旋相反的两倍. 然而,色散相互作用为电子间的电磁相互作用与电子的自旋并无直接关系,自旋相同与自旋不同电子间色散相互作用能应该相等. 对于He2体系,我们前期的工作指出E类激发组态波函数仅能得到自旋不同电子间色散相互作用能的一半. 估算体系的色散相互作用能应在式(12-15)求和的基础上再乘以系数4/3. 因此,该体系的色散相互作用能可近似为下式:
(16)
3 计算结果与讨论
本文我们讨论两相互平行的氢分子在以下两种情况下的色散相互作用能.
第一种情况:两个氢分子都处于平衡位置附近(RH-H=1.4 a.u.),研究色散相互作用能随两氢分子间距的变化(6 a.u. (17) 由于SAPT理论对处于非平衡体系将失效. 因此,式(16)计算得到的第二种情况下色散相互作用能将和远程的色散项C6/R6直接进行对比. 该色散项能够非常精确的估算体系远程的色散相互作用能.C6通过直接积分 Casimir-Polder 方程得到[27]. α(iω)为偶级极化率,由CCSD理论水平下的响应理论计算得[28]. 表I和表II分表罗列出以上两种情况下的计算结果. 以上所有计算均在 aug-cc-pvTZ 基组下进行. 对于第一种情况, 式(16)的计算结果与 SAPT 非常接近. 最大的误差百分比仅为8.33 %. 当R< 8.0 a.u. 时, SAPT 理论计算得到的色散相互作用能比式(16)要大. 但在R> 8.0 a.u. 区域, 式(16)的计算结果要比 SAPT大. 表I 两相互平行的氢分子间色散相互作用能(RH-H=1.4 a.u.). 所有的计算在aug-cc-pvTZ基组下进行,数值单位为原子单位. 在第二种情况下,式(16)同样和远程的色散项C6/R6符合的较好. 当RH-H=1.4 a.u. 时有最大误差百分比 17.94 %. 该误差百分比将随RH-H的增大而逐渐减小直到RH-H> 3.5 a.u.. 式(16)的计算结果在这些位置都比C6/R6大. 这是由于远程的色散项C6/R6并不包含高阶色散项. 因此,C6/R6一般比精确值要小. 例如:表I显示在RH-H=1.4 a.u.处,式(16)与 SAPT 的误差百分比仅有-2.57 %. 当RH-H> 3.5 a.u.时,式(16)的结果比色散项C6/R6的值还要小. 这是因为在这些位置将会有更多的组态波函数具有和基态行列式Ψ0可比拟的展开系数(氢分子处于离解区域时非动态关联效应明显). 这时仅考虑ΨE(a)和Ψ0的乘积对二阶密度矩阵的贡献不再是个很好的近似,多参考组态效应需要考虑,本文对此不作深入讨论. 由此可见,式(16)对两氢分子间色散相互作用能的确能够给出较准确的估算. 表II 两相互平行的氢分子间色散相互作用能(两氢分子间距R= 7.0 a.u.). 所有的计算在aug-cc-pvTZ基组下进行,数值单位为原子单位. 本文通过计算来源于E类双重激发组态波函数的电子间相互作用能来估算两相互平行的氢分子间色散相互作用能. 通过和高精度的从头计算(SAPT和CCSD)进行比较,表明该方法合理有效. 研究表明,精确描述该体系中的色散相互作用能的自然轨道泛函形式为: [〈kgku|numg〉-〈kgku|mgnu〉] (19) 其中,k取遍所有轨道占据数nkg/u>1的强占据轨道,m,n表示所有占据数nmg,nnu< 1的弱占据轨道.fxcdisp为自然轨道占据数泛函. 该泛函中的每个积分含有4个轨道,并非是目前密度矩阵泛函广泛使用的交换和库伦积分泛函. 因此,现有的密度矩阵泛函并不包含有体系的色散相互作用能. 要得到精确计算色散相互作用能的密度矩阵泛函还需要知道fxcdisp的具体形式,这将是我们今后的工作.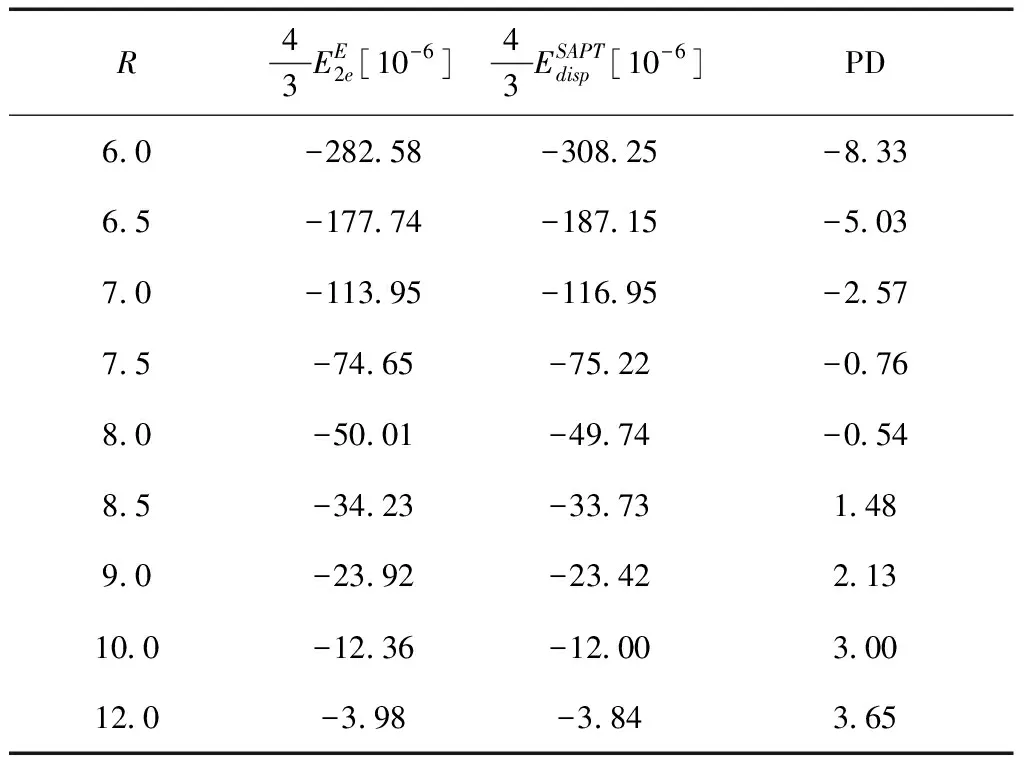

4 结 论
