扭矩与外压联合作用下海底管道的屈曲研究
2022-03-04胡少谦韩梦雪余建星刘泽生
余 杨 ,胡少谦 ,韩梦雪 ,余建星 ,刘泽生
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 天津大学天津市港口与海洋工程重点实验室,天津 300072)
海底管道被称为海上油田的“生命线”,一旦发生事故会造成巨大的环境破坏和经济损失,其安全研究至关重要[1].海底管道在铺设和服役期间可能同时受多种载荷的作用,在铺管过程中的扭矩已经被学者注意到,其会对管道结构和安全产生一定影响[2-3];在钢悬链立管(SCR)中,因浮体运动和波浪流作用,管道可能发生扭转,进而影响管道的安全[4].此外,随水深的增加,管道在外压下的压溃和屈曲是深水海底管道主要的失效模式之一[5],国内外学者对管道在外压、弯矩或轴力等载荷共同作用下的屈曲破坏问题进行了大量的研究[6-9],管道在扭矩和外压联合作用下的破坏机理仍需进一步分析.
Arghavan等[10]考虑空心管截面形状,推导了薄壁至中厚壁管结构受扭矩作用的解析公式. Mahmoud等[11]通过实验研究了钢管在循环扭矩作用下的力学响应,探索不同扭转角度、历史加载和开口缺陷对钢管性能的影响.管道扭转变形的截面基本平坦,壁厚增加会使管道抗扭能力增强,扭矩的顺逆施加方向对均质管道的承载能力没有明显影响[12-14].Mohsen等[15]在修正的莫尔-库伦准则的基础上,利用有限元模型研究了管道在轴向拉力和扭矩作用下的力学行为.Sharma等[16]针对空心厚壁管结构,提出了在扭矩和外压作用下的外压承载力理论计算公式,研究表明,扭矩会降低管道外压承载力,但尚未给出扭矩与外压联合作用下的承载力变化规律.余建星等[17]研究了全尺寸海底管道在扭矩与外压共同作用下的屈曲,对壁厚、一致椭圆度和外径对压溃压力的影响进行了分析.
上述研究以管道整体变形和不同因素敏感性分析为主,管道受扭矩和外压联合作用的截面变形和承载极限变化规律需进一步研究.为解决上述问题,进行了缩比尺管道扭矩与外压联合加载实验,研究管道的屈曲压溃,建立与实验条件完全相同的有限元模型,与实验结果作对比,验证模型可靠性.基于有限元分析,研究海底管道在扭矩和外压作用下的变形规律和承载极限,拓展管道受扭矩和外压作用的研究内容,为海底管道的安全校核提供依据和补充.
1 缩比尺管道实验
1.1 材料本构关系
管道的屈曲分析中,Ramberg-Osgood模型可以对材料的非线性进行比较准确的描述,其中R-O方程原型[18]为

式中:ε为应变,无量纲;σ为应力,MPa;E为材料弹性模量,MPa;k为强度系数,无量纲;n为应变硬化指数,无量纲.
经过处理后,方程可变形[19]为

式中:0σ为屈服应力,MPa;0ε为屈服应变,无量纲;α为R-O系数,无量纲.
根据实验钢管(SS304)材性实验得到材料的应力应变曲线,确定本次实验钢材屈服应力等参数,通过修正公式(2)参数,得到R-O拟合曲线并与材性实验作对比,见图1.最终确定管道材料参数见表1.
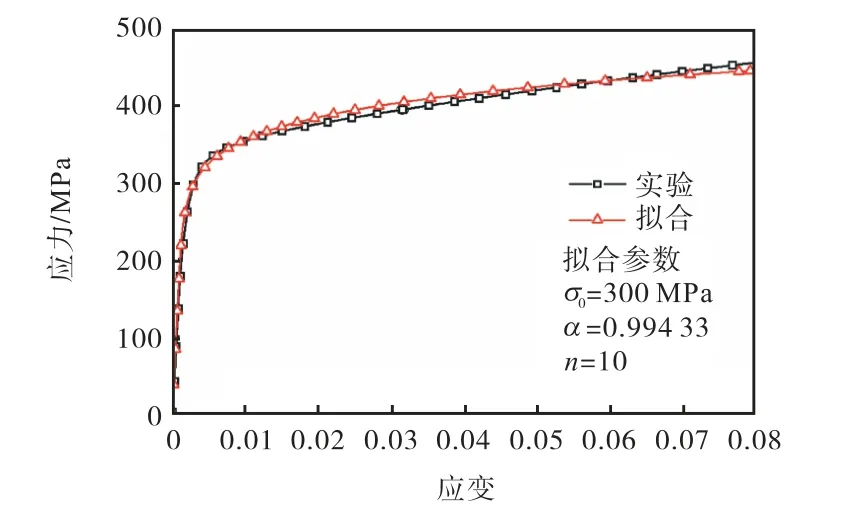
图1 材料应力-应变关系Fig.1 Relationship between material stress and strain

表1 管道材料参数Tab.1 Material properties of the pipe
1.2 管件预处理
实验管件参数见表2,管件两端焊接法兰,方便固定装载,在实验前加工局部椭圆度缺陷,其计算公式如下:
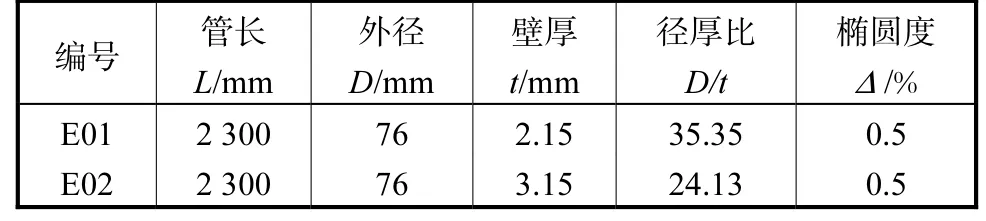
表2 管件尺寸参数Tab.2 Pipe size parameters

式中:Dmax与Dmin分别为最大和最小外径;D为平均管道外径根据规范要求[20],海洋管道铺设前的初始椭圆度缺陷应不大于3.0%.
1.3 缩尺比管道压溃实验
图2中是天津大学深水结构实验室缩尺比高压实验舱,具有同时加载扭矩和水压的能力.进行了两组缩比尺管道实验,载荷施加顺序为先扭矩、后外压.两根钢管仅壁厚不同,实验采用位移转角控制,加载的扭转角为0.6rad,并在随后实验过程中保持不变.其后,向实验舱内打水加压,直至钢管压溃,同时记录实验数据.

图2 缩尺比高压实验舱Fig.2 Reduced-scale hyperbaric chamber
1.4 实验结果
实验水压变化如图3所示.在此过程中,舱内水压逐渐增加到管件外压承载最大值,即外压承载极限(PM),随后管件压溃,舱内水压骤降.到达最低点后水压有所增加并保持稳定,其原因为:管件材料具有弹塑性,管件发生压溃大变形后,反向回弹恢复,使舱内水压增加,并保持稳定.从图中也可以看出,壁厚越大,外压承载极限越大,屈曲后稳定时的舱内水压也越大.
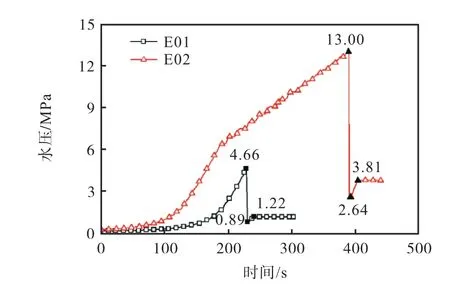
图3 水压加载曲线Fig.3 Hydraulic loading curve
实验完成后管件压溃情况如图4所示,管件上的纵向和环向标记线有所扭曲,表明压溃后的管件存在一定的残余扭转变形.E01和E02的压溃变形相似,屈曲长度不同,这与压溃时舱内水压下降幅值大小相对应.

图4 管件压溃示意图Fig.4 Schematic of pipe collapse
2 有限元模型
2.1 建模及收敛性检验
采用ABAQUS隐式动力算法模拟管道在扭矩与外压作用下的屈曲破坏.考虑到管道在屈曲压溃前的变形缓慢,动力效应忽略不计,选择准静力分析.管道模型参照表2中的E02,使用线性减缩积分(C3D8R)单元.图5为管道载荷作用示意图,有限元模型受载形式与实验完全相同,载荷加载顺序为:先扭矩、后外压(T-P路径).管道右端固支;左端铰支,仅允许轴向(沿z轴)移动和轴向转动.管左端受扭矩作用(T),外表面受均匀分布的压强载荷(P).具体载荷加载分为两个分析步.分析步一:扭矩加载;分析步二:扭矩载荷不变,外压加载.后文中涉及的P-T路径载荷加载方式如下.分析步一:外压加载;分析步二:外压载荷不变,扭矩加载.
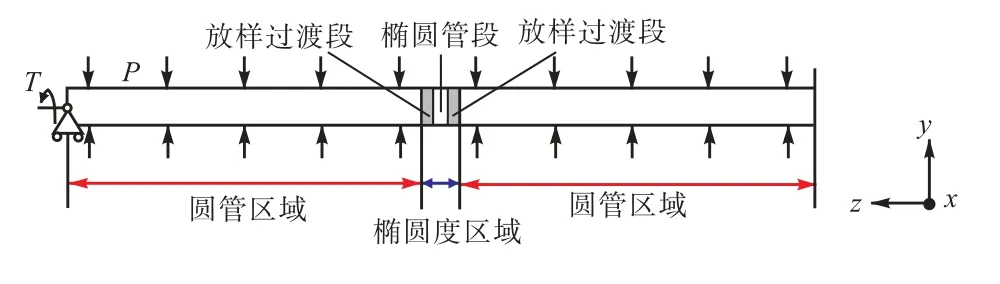
图5 载荷加载示意图Fig.5 Schematic of loading
考虑到椭圆度区域会出现应力集中,细分了其轴向网格数量,管道网格划分如图6所示.改变网格疏密,将不同网格的计算结果汇总于表3.随网格数目的增加,水压承载极限逐渐稳定,计算结果收敛.考虑时间成本和结果精确性,模型采用第4组网格划分方式.
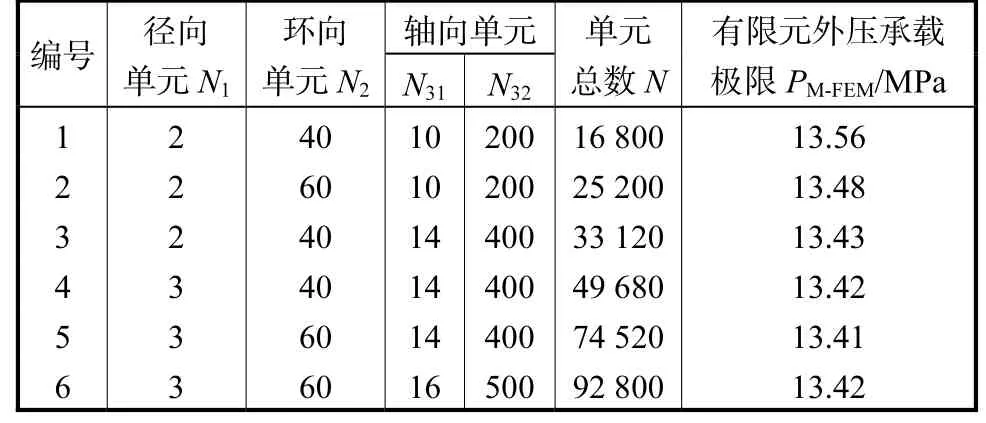
表3 网格收敛性检验Tab.3 Convergence test of mesh
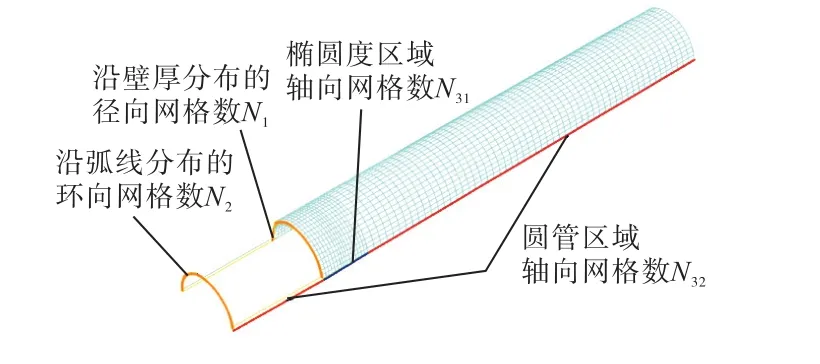
图6 管道网格划分示意图Fig.6 Schematic of pipe meshing
2.2 有限元结果验证
表4是有限元模型的计算结果与实验结果的误差统计,有限元模型的结果误差范围在5%以内,达到工程应用的误差要求,同时也验证了有限元模型的准确性与可靠性.
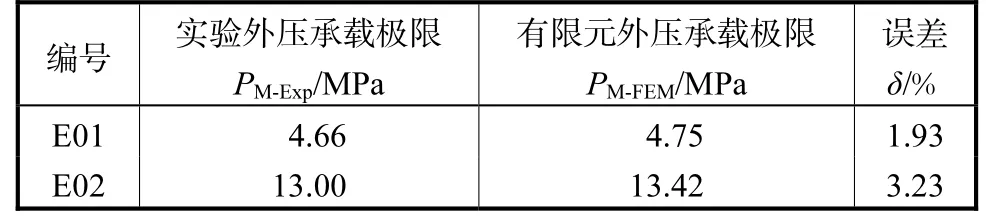
表4 实验结果及有限元验证Tab.4 Experimental results and finite element verification
图7是有限元模拟的管道压溃图,屈曲压溃区域从椭圆度缺陷位置向两端传播.3处截面图均为“哑铃状”[20],但发生的扭转角度不同,说明管道压溃后存在扭转变形,与实验结果相对应.从管道压溃的整体变形和截面变形来看,有限元模拟结果与实验结果吻合较好.综上所述,具有局部椭圆度的管道有限元模型准确可靠.
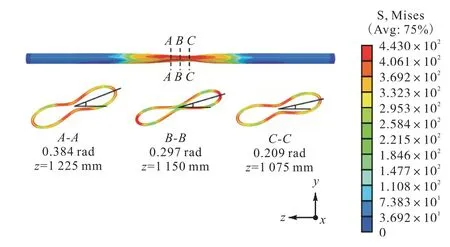
图7 有限元模拟结果Fig.7 Finite element simulation results
3 有限元分析及结果
3.1 管道的变形
以长度2300mm、截面尺寸76mm×3.15mm、局部椭圆度为0.5%的管道模型为基本研究对象进行管道变形和承载极限分析.通过有限元模拟,可以更直观地研究管道在扭矩和外压载荷下(T-P)的变形过程.在管道压溃前,管道的变形主要表现为具有局部椭圆度管段横截面的形状变化,以截面的椭圆度大小来度量其变形程度.
管道变形的截面上,应力集中分布的位置在长轴和短轴.如图8所示,1、2两点是长轴外壁点和内壁点,3、4两点是短轴外壁点和内壁点.管截面椭圆度由1、3两点的坐标间接计算得出.
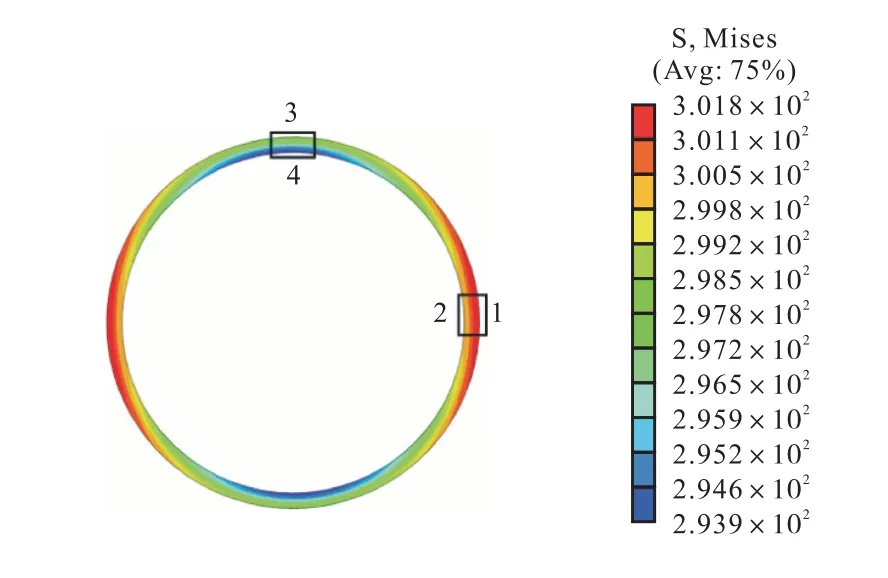
图8 截面应力分布Fig.8 Sectional stress distribution
图9是管道在扭矩和外压共同作用下的截面标记点应力变化及截面变形情况.分析步1.0之前,是扭矩作用阶段;1.0~1.671是扭矩和外压同时作用阶段.扭矩作用阶段各点已经达到屈服应力,但是椭圆度变化很小,从0.5%增加到0.547%;扭矩和外压共同作用阶段,应力变化不大,椭圆度迅速增加.得到初步结论:扭矩载荷对椭圆度影响较小,外压载荷对椭圆度影响显著.
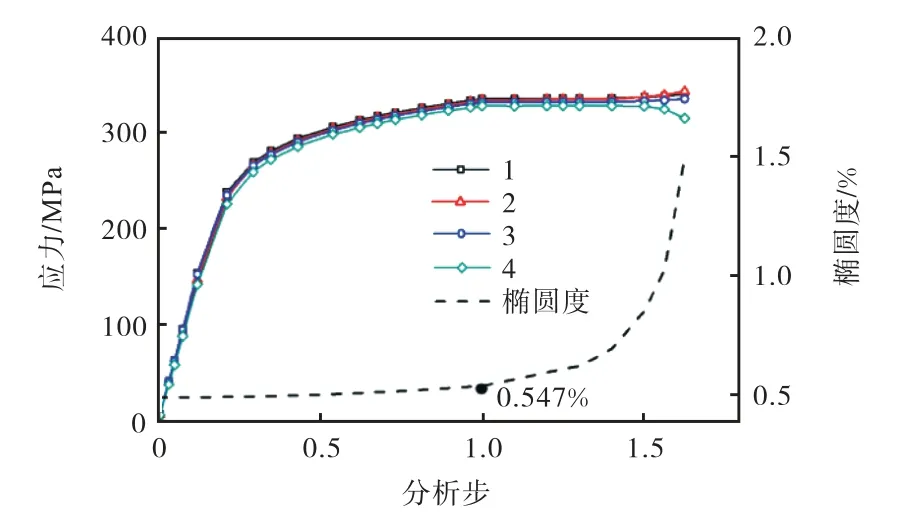
图9 扭矩与外压载荷下的应力及变形Fig.9 Stress and deformation under torsion and external pressure load
外压对有椭圆度缺陷的管道变形的影响主要表现为截面长轴外扩、短轴内缩、压溃后呈“哑铃状”[21].扭矩对管变形的影响主要是管的扭转变形,上述研究中未体现出管道的扭矩承载极限(TM),需进一步研究.
图10中,材料屈服前,随管道扭转角度的增加,扭矩力迅速线性增加;材料屈服后扭矩力的增加逐渐平缓稳定;达到最大扭矩力之后,扭矩力下降.图中有4个数值标记点及其对应的截面图,Γ是变形放大系数.定义管道扭矩承载极限为最大扭矩力(5.86kN·m),在扭矩承载极限之后,管结构发生严重破坏,椭圆度不再适用于描述其变形程度.在接近扭矩极限的96%(5.63kN·m),椭圆度曲线斜率超过扭矩曲线斜率,其后,椭圆度增速越来越大.总之,扭矩较小时,椭圆度基本无变化,扭矩接近扭矩承载极限时,椭圆度剧增,椭圆度与扭矩是近似指数相关.
图11是扭矩载荷下的管道整体变形,应力主要集中在椭圆度缺陷附近.管道扭转破坏后,管道两侧区域应力相比破坏前有所下降,这是因为此时管道承受的扭矩力下降,与图10中曲线最后部分相对应.
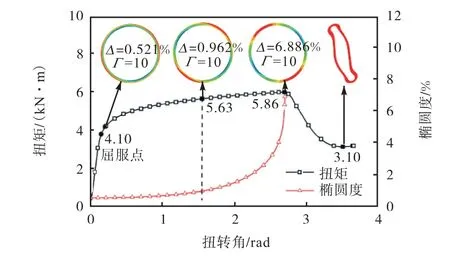
图10 扭矩载荷下管道截面变形Fig.10 Pipe section deformation under torsion load

图11 扭矩载荷下管道整体变形Fig.11 Whole pipe deformation under torsion load
考虑到实际工况,管道的扭转角度一般较小,不会直接破坏.不过,小扭转角会引起大扭矩力,进而管道在外压作用下发生压溃屈曲,这是管道受扭矩与外压作用的主要破坏形式.目前已知扭矩对海底管道的变形影响有限,第3.2节将研究扭矩对管道外压承载能力的影响.
3.2 管道的外压承载极限
管道受扭矩和外压共同作用时(T-P),管道的外压承载极限与管道的安全性能紧密相关.就不同椭圆度管道的外压承载极限进行了计算,并针对扭矩载荷进行敏感性分析,将结果汇总于图12.各组模型中,外压承载极限随椭圆度的增大而显著降低.图中每组曲线趋势相似,随施加扭矩的增大管道的外压承载极限逐步降低,且下降速率不断增大.
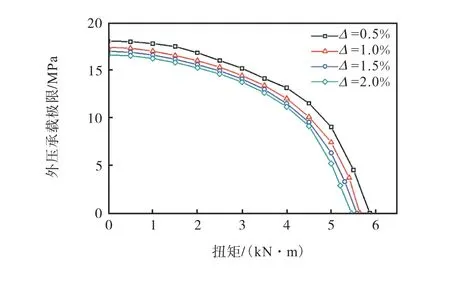
图12 外压承载极限对扭矩的敏感分析Fig.12 Sensitivity analysis of external pressure bearing limit to torsion
图13是将图12中数据进行无量纲化处理,并增加两组不同管道外径的模型数据,得到扭矩与管道外压承载极限的无量纲关系.无量纲扭矩(TN/M)是实时扭矩(TN)与扭矩承载极限(TM)的比值,无量纲外压承载极限(PM/M0)是实时扭矩对应的外压承载极限(PM)与无扭矩作用时的外压承载极限(PM0)的比值.由该图可见,不同椭圆度、外径的关系曲线基本重合,表明椭圆度和外径对此关系基本无影响.随扭矩的增加,外压承载极限下降速率也越大.该曲线可为工程实际提供参考,预估扭矩对管道外压承载能力的影响.为方便研究,对图13中的趋势曲线进行拟合,拟合系数R2=0.9914,得到公式如下:
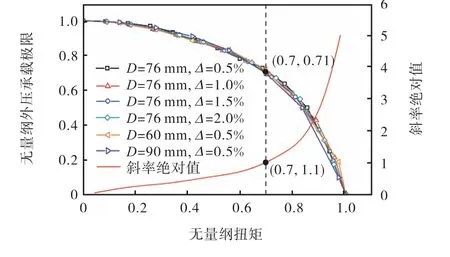
图13 扭矩与外压承载极限的关系Fig.13 Relationship between torsion and external pressure bearing limit
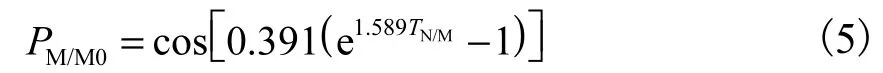
利用上述公式可预估海底管道外压承载能力受扭矩的影响大小.以椭圆度为0.5%的管道为例,当扭矩增加幅值达到70%,外压承载极限下降幅值会达到30%左右.注意到,在无量纲扭矩为0.7时,下降曲线的斜率绝对值为1.1,表明无量纲扭矩的增加速度已经小于其对应无量纲外压承载极限的下降速度,此后扭矩对外压承载极限的负面影响会更显著.文献[22]中也采用相似的研究方法,研究了管道的承载能力.所以笔者建议,管道设计扭矩不超过管道扭矩承载极限的70%.
3.3 载荷路径对管道承载极限的影响
管道在铺设过程中一般先受扭矩,后受外压,对应载荷路径为T-P路径.而服役中的管道先受外压,后受扭矩,对应载荷路径为P-T路径.本文研究了不同载荷路径下管道达到承载极限时扭矩与外压的关系,探究载荷路径对管道承载极限的影响.
以T-P路径下得到的外压承载极限为基础,将外压作为P-T路径下第一载荷值,第二载荷为扭矩作用,计算得到扭矩承载极限,如图14所示,在相同椭圆度下,T-P路径的关系曲线在P-T路径右上方,说明同样的外压条件下(相同水深),P-T路径相对更危险.同时,不同的椭圆度下都是P-T路径更危险,所以椭圆度对危险路径的类型无影响.
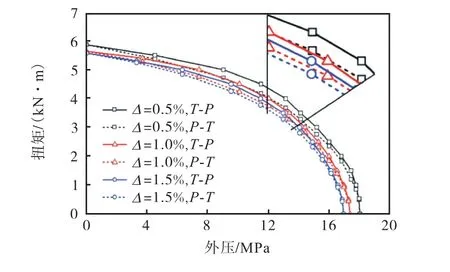
图14 载荷路径对管道承载极限的影响Fig.14 Influence of loading path on pipe bearing limit
以不同载荷路径、相同外压对应扭矩的差异大小来表征载荷路径对管道承载极限的影响程度.如图15所示,随外压增大(水深增加),不同路径下扭矩差异也越大.鉴于在实际工程中,管道设计会预留一定的安全余量,管道承受的外压一般不会接近外压承载极限,所以不同载荷路径对管道承载极限的影响可认为在10%以内,从保守的角度出发,可以依据T-P路径下扭矩与外压承载极限关系来设计管道.随椭圆度增大,扭矩差异有所减小,说明椭圆度会减小载荷路径对管道承载极限的影响.
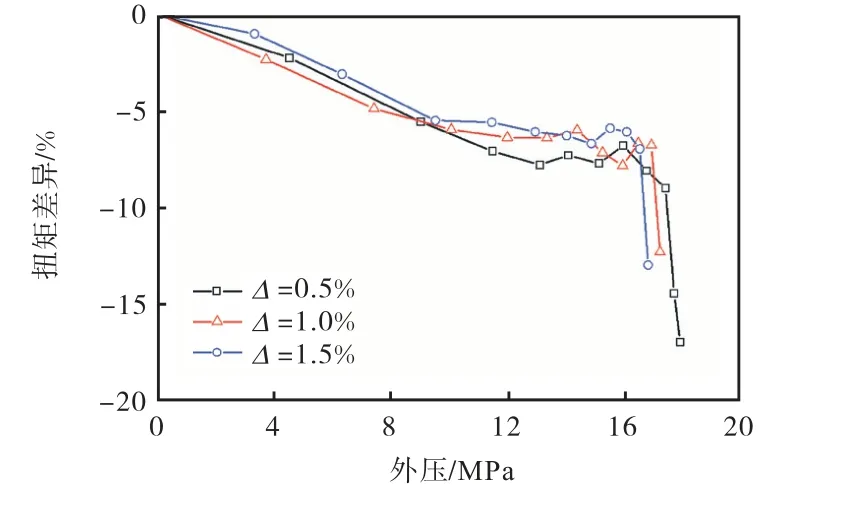
图15 不同载荷路径下扭矩差异Fig.15 Torsion difference under different loading paths
4 结 论
(1) 管道在纯扭矩作用下,扭矩较小时,截面椭圆度变化不明显;当扭矩接近扭矩承载极限时,椭圆度剧增,椭圆度与扭矩近似指数相关.管道在扭矩和外压共同作用时,椭圆度在有外压作用的阶段发生明显变化,管道最终压溃截面呈“哑铃状”.
(2) 管道在扭矩与外压共同作用下,椭圆度越大,外压承载极限越小;扭矩越大,外压承载极限越小,外压承载极限下降速率越大.
(3) 绘制了扭矩与外压承载极限的关系曲线,得到无量纲关系,为工程实际提供参考;提出建议,管道设计扭矩不超过扭矩承载极限的70%.
(4) P-T载荷路径比T-P载荷路径更危险,外压(水深)越大,两路径对应破坏扭矩差异越大;载荷路径对管道承载极限的影响在10%以内,椭圆度会降低载荷路径的影响差异.
