玻璃纤维网格超高性能混凝土板抗弯性能试验研究

邓宗才，鹿宇浩，龚明高，桂营金，景晓斌

(1. 城市与工程安全减灾省部共建教育部重点实验室(北京工业大学)，北京100124；2. 北京怀仁前景工程技术有限公司，北京102400)

在海洋、盐碱和其他易受腐蚀介质侵蚀的环境中，钢筋混凝土结构的耐腐蚀性能引起了人们的普遍关注，钢筋锈蚀是影响混凝土结构耐久性最主要的因素[1]．随着合成纤维网格的出现，连续纤维增强混凝土(textile reinforced concrete，TRC)应运而生．TRC是一种新型纤维网格增强水泥基复合材料，与传统钢筋相比，纤维网格抗腐蚀性能更优越、种类更多、材质更轻，且在径向和纬向均具有较高抗拉强度，能够沿着构件主应力方向布置，从而有效增大构件抗拉强度，因此TRC在结构修复加固和建造新型轻质结构等领域得到了广泛应用[2-5]．

但纤维网格与混凝土均为脆性材料，为了降低TRC破坏时的脆性，提高其抗裂能力和变形能力，国内外众多学者通过掺入钢纤维来改善TRC构件的变形性能[6-8]．但是高掺量钢纤维成本高昂，低掺量钢纤维增韧作用有限，因此有研究者将不同强度、弹性模量、尺度的短切纤维进行合理混掺，制备出低成本、高性能的TRC，形成优势互补，成为改善TRC力学性能的新的研究方向．Barhum等[9]研究了外掺短切碳纤维对玻璃纤维网格TRC轴拉性能的影响，发现当短纤维体积率为1%时，其初裂应力和断裂能显著增加，短切碳纤维有效改善了网格与基体的界面黏结性能，试件破坏时裂缝细而密．Park等[10]研究了5种不同长度和形状的钢纤维混掺对混凝土拉伸性能的影响，结果表明随着微钢纤维掺量的增加，混凝土拉伸韧性得到显著改善．Guo等[11]通过弯曲、准静态和动态劈裂拉伸试验，研究了钢纤维和聚丙烯纤维混杂对高强混凝土的增韧效果，结果表明混掺2.5%钢纤维和0.12%聚丙烯纤维时，纤维高强混凝土的准静态和动态劈裂拉伸韧性达到最佳．

目前关于混杂纤维TRC的研究主要局限于砂浆和普通混凝土，影响了TRC在结构加固、桥梁、海洋工程等领域的应用．近年来，超高性能混凝土(ultrahigh performance concrete，UHPC)凭借其超高强度、高韧性和超高耐久性，逐渐成为极具竞争力的水泥基复合材料[12-14]．然而如何降低UHPC脆性是工程界关注的热点问题．通过在UHPC中掺入短切纤维、铺设纤维网格来提高UHPC强度和韧性具有重要的工程应用价值[15-16]．但目前关于混杂纤维、纤维网格对UHPC板增强增韧效应的研究还鲜见报道.

本文参考欧洲EFNARC规范[17]，采用四边简支双向板试验，研究玻璃纤维网格层数和混杂纤维对UHPC板的增强增韧作用，分析玻璃纤维网格层数、混杂纤维种类及掺量对UHPC板的力学性能的影响规律．

1 试验概况

1.1 试验材料

试验用的网格是由山东泰山玻璃纤维有限公司提供的ARNP300高锆耐碱玻璃纤维网格(glass fiber net，GFN)，网孔尺寸为5mm×5mm(见图1)，其性能参数见表1．试验中UHPC基体配合比见表2，其中水泥为P·Ⅱ·52.5R；硅灰为埃肯国际贸易(上海)有限公司生产的Elkem951级硅微粉，其二氧化硅含量不小于95%，950℃烧失量不大于1%；矿粉为S95级粒化高炉矿渣粉；细骨料为3种不同目数的机制河砂．

表1 玻璃纤维网格力学性能参数Tab.1 Mechanical property parameters of the glass fiber net

表2 UHPC基体配合比Tab.2 Composition ratio of the UHPC

1.2 双向板制备

试验共制备15个双向板，尺寸均为500mm×500mm×50mm，根据铺设的GFN层数不同分3组，第1组未铺设GFN，第2组、第3组分别铺设2层和3层GFN，每组5个试件．试验共设计5类不同纤维混掺比例，其总体积率均为1.5%，分别为单掺1.5%钢纤维(steel fiber，SF)、1.0%钢纤维与0.5%聚乙烯醇纤维(polyvinyl alcohol，PVA)混掺、0.5%钢纤维与1.0%聚乙烯醇纤维混掺、0.5%钢纤维与1.0%玻璃纤维(glass fiber，GF)混掺、0.5%钢纤维与1.0%玄武岩纤维(basalt fiber，BF)混掺．其中每组第1个板只掺钢纤维，其余4个板为混杂纤维．各类短切纤维物理性能见表3，试件编号及纤维体积率见表4．

表3 短切纤维性能参数Tab.3 Performance parameters of the chopped fiber

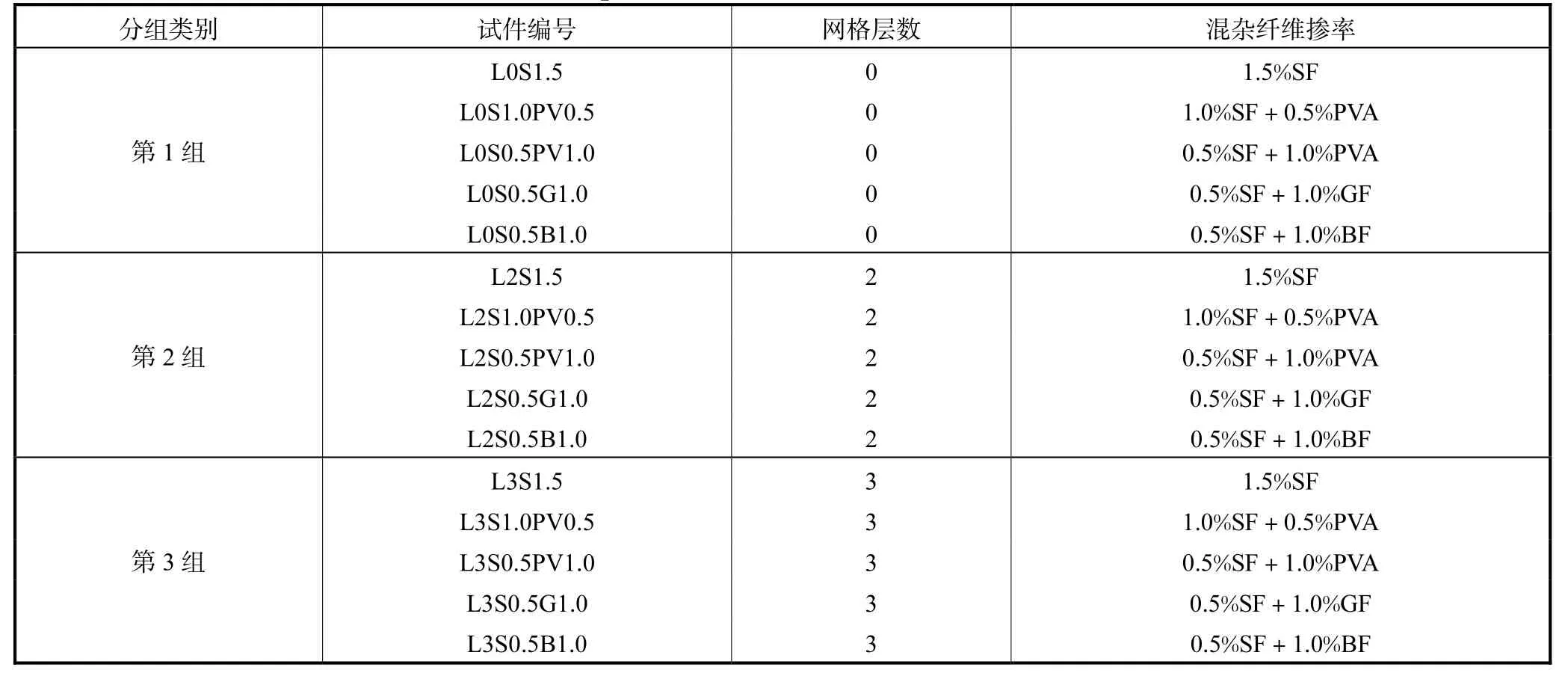
表4 试件编号与纤维体积率Tab.4 Specimen number and fiber volume ratio

试验采用分层浇筑法成型，浇筑时将GFN布置于双向板的受拉一侧，对于铺设多层网格的板，相邻网格间距为3mm．以2层GFN试件为例说明浇筑过程：第1步将500mm×500mm的木模具放平，浇筑42mm的UHPC；第2步将第1层GFN用3mm厚木板压条固定于模具边框上(GFN厚度约为1mm)，浇筑3mm UHPC；第3步将第2层GFN用3mm厚板条固定于模具边框上，浇筑3mm UHPC．3层GFN试件浇筑过程与之相似．完成后将试件在(20±2)℃、相对湿度＞90%条件下养护24h后脱模，并进行标准养护25d，试验前2d取出晾干．

1.3 加载方式

试验时，将双向板四边置于刚性支架上，在板顶中心通过80mm×80mm预制钢块和150mm×150mm钢板传递集中荷载，加载过程采用液压伺服控制，加载速率为0.5mm/min．在两侧的刚性支架上各固定一个位移计，以测量板的中心挠度，同时在板底中心和板顶钢板四周各粘贴两个混凝土应变片测量其应变变化，使用数据采集系统同步记录所有数据.

加载测量装置及加载方式见图2和图3．

图2 双向板加载测量装置Fig.2 Two-way slab loading measuring device

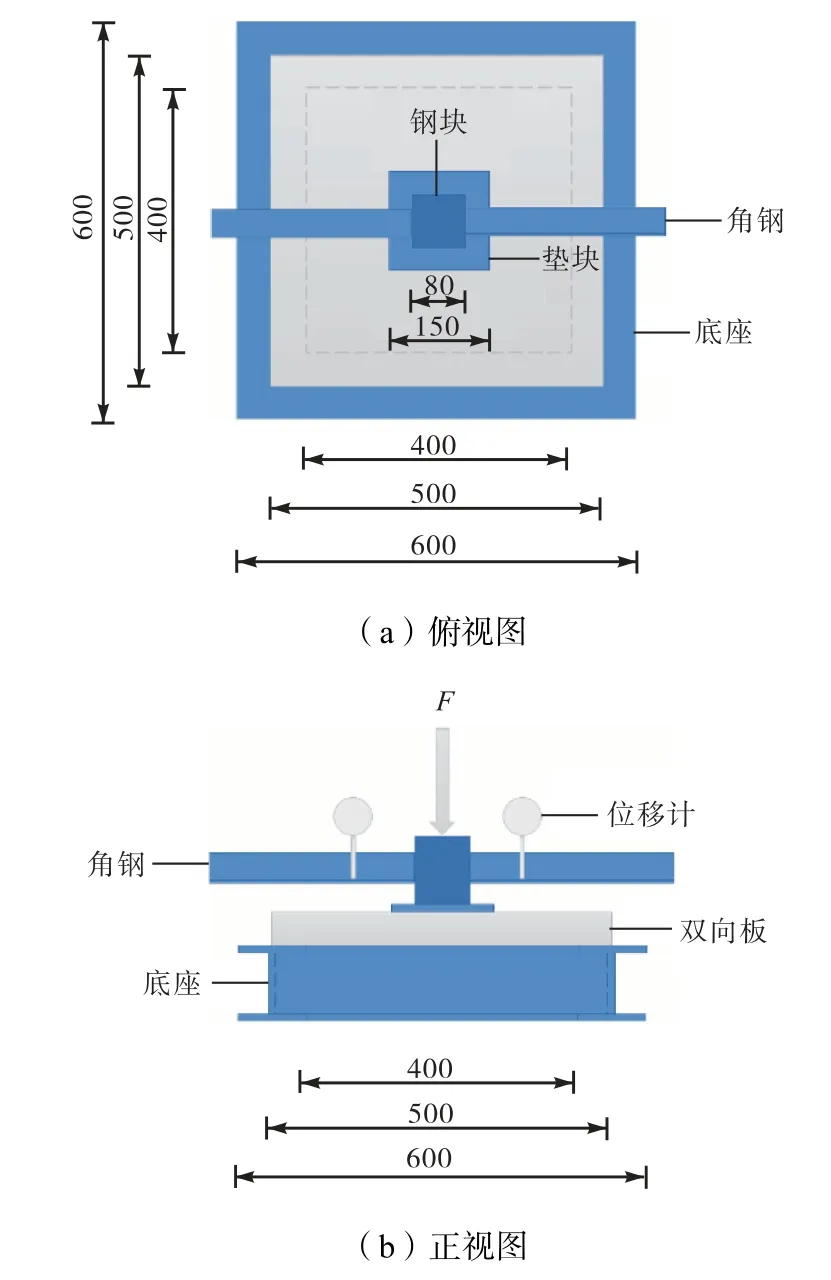
图3 双向板加载方式Fig.3 Loading mode of the two-way slab

2 试验结果及分析

2.1 UHPC板弯曲破坏阶段及破坏形态

2.1.1 UHPC板弯曲破坏阶段

基于先前研究[18-19]，铺设GFN时四边简支混凝土双向板的荷载-挠度曲线趋势一般如图4所示．由图4可知双向板在承受集中荷载时，从加载开始至完全破坏经历了3个阶段：Ⅰ为线弹性阶段，在该阶段认为双向板是理想的线弹性材料，荷载由混凝土和纤维网格共同承担，同时荷载-挠度曲线近似为直线，结束的标志为板底混凝土达到初裂荷载，底部中间出现第1条裂缝；Ⅱ为基于应变的应变硬化阶段，在第1条裂缝出现后，因为短切纤维的存在，应力将通过裂缝两侧纤维桥接传递，随着荷载不断增大，裂缝处短切纤维不断被拉断和拔出，荷载出现短暂下降，此时双向板内部开始发生内力重分布，裂缝处的承载力开始由纤维网格承担，使得荷载进一步增大，开始出现第2条裂缝，同时内力重分布继续发生，直至纤维网格达到极限抗拉强度被拉断，承载力开始下降，该阶段结束；Ⅲ为基于裂纹扩展的应变软化阶段，在该阶段不再有新的裂缝出现，初始裂缝开始扩展成主裂缝，随着纤维网格应变增加和纤维不断被拉断，荷载逐步下降，直至双向板丧失承载能力．

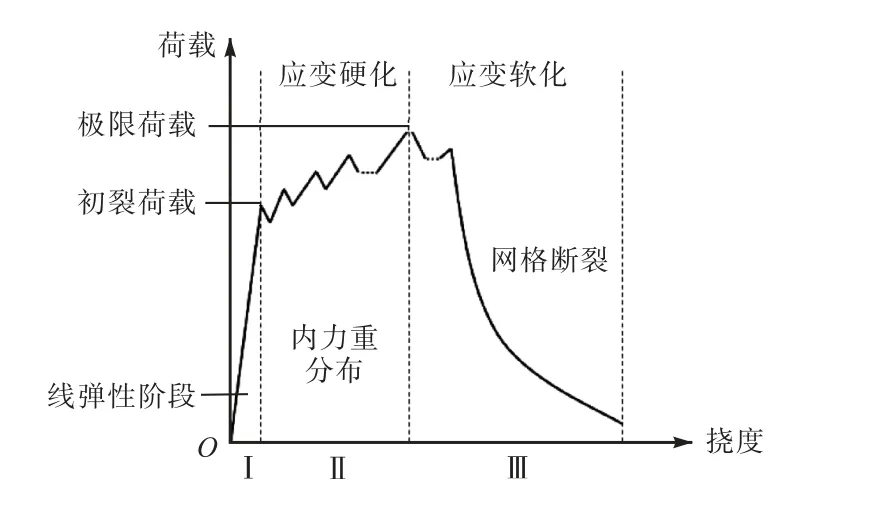
图4 玻璃纤维网格UHPC板荷载-挠度曲线Fig.4 Load-deflection curve of UHPC slabs with GFN

2.1.2 UHPC板弯曲破坏形态

图5为不同GFN层数的UHPC板破坏形态，由图5可知，未铺设GFN的第1组试件L0S1.5的主裂缝数量为7条，其余混杂纤维的主裂缝数量为5条或6条，表明混掺非金属纤维会抑制UHPC板裂缝数量的增加，但较单掺SF在破坏时脆性特征明显，试件L0S1.5、L0S1.0PV0.5较其他混杂纤维UHPC板微裂缝更多，表明随着SF体积率的增加，试件裂缝发展更充分，当SF增加到1.5%时试件在板底中心处形成环形裂缝，其余裂缝由中心向四周扩展，贯穿板面.

铺设2层和3层GFN试件的主裂缝数量为4、5条，其数量及宽度均明显小于未铺设GFN试件，且3层GFN试件板面出现的微裂缝明显多于2层，表明GFN能够有效抑制主裂缝扩展，增加微裂缝数量，且层数越多微裂缝数量越多．

2.2 UHPC板承载力的主要影响因素

2.2.1 PVA体积率的影响

表5为各试件的初裂、极限荷载及其对应挠度值．由表5可知，未铺设GFN的第1组试件L0S1.5、L0S1.0PV0.5、L0S0.5PV1.0的极限荷载分别为39.40kN、52.68kN、34.36kN，表明当混杂纤维总体积率为1.5%时，随着SF体积率减小以及PVA体积率的增加，UHPC板的极限承载力表现出先上升再下降的趋势，其中1.0%SF和0.5%PVA混杂效果最好，且初裂荷载较单掺1.5%SF提升幅度超过50%．这是因为当混杂少量PVA纤维时，具有亲水性的PVA能与水化反应产物充分黏结，增强了UHPC界面黏结力，同时PVA纤维能够桥接细小裂缝，延缓宏观裂缝的形成，表现出对初裂荷载提升显著的特征；当混杂过量PVA纤维时，纤维易成团，在UHPC内部不能均匀分散，导致不均匀界面增多，因此对初裂荷载提升有限[20]．试件L0S1.5、L0S1.0PV0.5、L0S0.5PV1.0在达到极限荷载时挠度分别为6.03mm、1.82mm、1.20mm．根据文献[21]，受弯构件正常使用极限状态的挠度限值为l0/200，l0为构件计算跨度，这里取2.5mm．此时试件L0S1.0PV0.5、L0S0.5PV1.0已发生破坏，丧失承载能力．

图6为不同PVA体积率下UHPC板荷载-挠度曲线．无论是单掺SF还是混掺SF与PVA纤维，UHPC板在应变软化段下降均较平缓，其中试件L0S1.5、L0S1.0PV0.5、L0S0.5PV1.0在挠度10mm处的荷载分别为34.97kN、30.54kN、18.02kN，其中单掺SF的UHPC板承载力下降最缓慢，峰后持荷能力最强，这是由于在达到极限承载力后SF因尺寸大、抗拉强度高，能更好地桥接宏观裂缝，峰后能够承受更大的荷载，而随着SF体积率降低及PVA纤维的中等强度和模量的特性，其桥接宏观裂缝的能力减弱，峰后持荷能力降低．

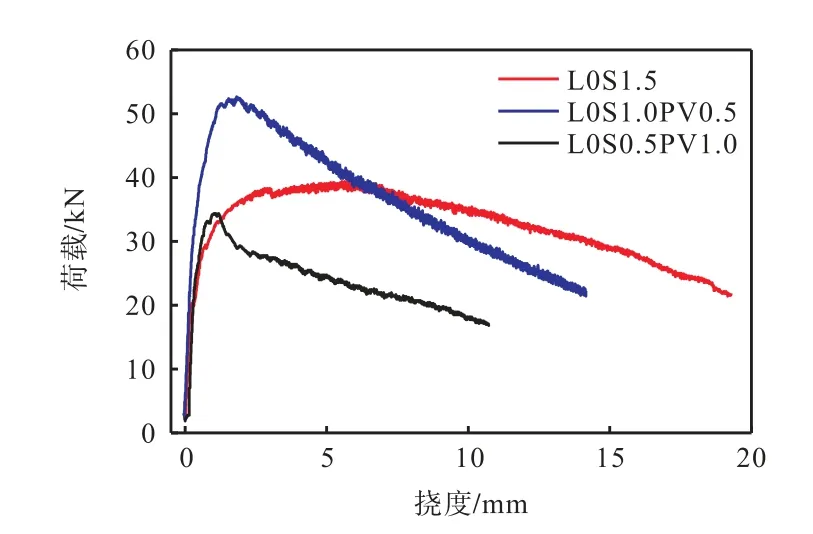
图6 不同PVA体积率下UHPC板荷载-挠度曲线Fig.6 Load-deflection curves of UHPC slabs with different PVA volume ratios

2.2.2 混杂纤维种类的影响

图7为不同纤维种类混杂UHPC板荷载-挠度曲线．由图7和表5可知，第1组试件L0S0.5PV1.0、L0S0.5G1.0、L0S0.5B1.0极限荷载分别为34.36kN、36.80kN、24.28kN，与试件L0S1.5相比分别降低了12.8%、6.6%、38.4%，其对应的挠度分别为1.20mm、1.18mm、2.91mm，L0S1.5的极限荷载对应的挠度分别是L0S0.5PV1.0、L0S0.5G1.0、L0S0.5B1.0的5倍、5.1倍、2.1倍，表明用1.0%的PVA、GF、BF替换1.0%的SF并不能增加UHPC板的极限承载力及其对应挠度．试件L0S1.5在应变硬化和应变软化阶段曲线发展均较饱满且平滑，达到极限荷载后承载力下降缓慢，而试件 L0S1.0PV0.5、L0S0.5G1.0、L0S0.5B1.0的应变硬化特性并不明显，在应变软化阶段曲线起伏较大，在挠度10mm 处试件L0S1.5的峰后残余荷载分别为上述3个试件的1.9倍、1.4倍、2.1倍，表明混掺非金属纤维的UHPC板在破坏时延性比掺同体积率的钢纤维低，持荷能力弱．这是因为非金属纤维的弹性模量和抗拉强度明显低于SF，且在裂缝处的桥联作用小于SF，受拉易断裂，使其增强作用比SF低[22-23]．

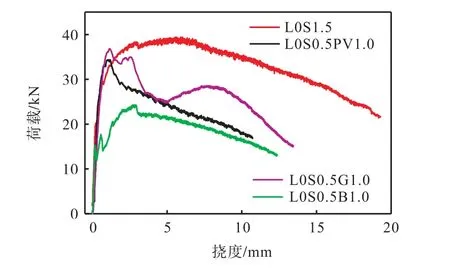
图7 不同纤维种类UHPC板荷载-挠度曲线Fig.7 Load-deflection curves of UHPC slabs with different fiber types

达到极限承载力后，随着挠度的增加，掺入GF的UHPC板表现出承载力回升的现象，且同长径比下，GF较BF对UHPC板极限承载力的提升更显著，这与文献[24]结论一致．同体积率下，相较PVA和GF，掺入BF的UHPC板极限承载力最小，但对应的挠度较大．

2.2.3 网格层数对混杂纤维UHPC板的影响

图8为不同GFN层数UHPC板荷载-挠度曲线．由表5可知，第3组试件L3S1.5、L3S1.0PV0.5、L3S0.5PV1.0、L3S0.5G1.0、L3S0.5B1.0的极限荷载分别为 82.15kN、102.00kN、71.46kN、84.96kN、71.16kN，较第2组试件分别提高12.3%、18.2%、6.1%、12.9%、7.3%，较第1组试件分别提高52.0%、48.4%、51.9%、56.7%、65.9%，这表明GFN能够显著增加板的极限承载力，且承载力随GFN层数的增加而增大．铺设2层和3层GFN的混杂纤维UHPC板极限荷载对应挠度较未铺设GFN试件均增加明显，其中0.5%SF和1.0%PVA混杂时挠度增加最明显，3层试件较2层增加73.1%，较0层增加612.5%．

由图8可知，所有铺设GFN的UHPC板在应变硬化阶段曲线均呈波浪形，表明相较未铺设GFN试件，铺设GFN的UHPC板在开裂后其内力重分布更充分；达到极限承载力后荷载-挠度曲线下降速率更快，这是因为GFN是脆性材料，当主裂缝处的GFN达到极限抗拉强度，部分网格突然断裂，承载力会发生突降，直到主裂缝处GFN大部分断裂，荷载开始由混杂纤维和剩余未断裂的网格承担，承载力下降变缓．

2.3 UHPC板的弯曲韧性

弯曲韧性表示纤维对混凝土开裂后的增韧效果，一般用塑性变形和破坏过程中吸收的能量来评价，其值等于荷载-挠度曲线下的面积[25]，其计算式为

式中：W为能量吸收值；a为板的中心挠度；F(x)是挠度为x时荷载值．

不同挠度能量吸收值计算结果见表6和图9．

2.3.1 混杂纤维种类对UHPC板弯曲韧性的影响

由表6、图9可知，当在UHPC板中不铺设GFN时，第1组试件L0S1.0PV0.5在1mm、2mm、5mm、10mm处能量吸收值分别为34.42J、86.37J、227.95J、408.45J，与其他混杂纤维试件相比在加载全过程能量吸收值均最大，其中在挠度10mm处能量吸收值较试件L0S1.5、L0S0.5PV1.0、L0S0.5G1.0、L0S0.5B1.0分别提升了14.3%、81.8%、46.1%、107.5%，表明在加载全过程1.0%SF和0.5%PVA纤维混杂对UHPC板弯曲韧性提升最显著．试件L0S0.5B1.0在各挠度下能量吸收值均最小，表明在全加载过程BF相较其他纤维对弯曲韧性的提升作用最弱．试件L0S0.5PV1.0、L0S0.5G1.0在挠度2mm处能量吸收值分别为55.28J、56.64J，较试件L0S1.5分别提升了5.4%、2.9%，在10mm处的能量吸收值分别为240.88J、279.63J，较试件L0S1.5分别提升了48.4%、27.8%，表明在挠度限值内，用1.0%的PVA、GF代替1.0%SF对UHPC板弯曲韧性的影响较小，超过挠度限值时，对弯曲韧性的提升存在负效应，这是因为相比GF、PVA，SF的抗拉强度更高，变形能力更小，在达到极限荷载后，SF对宏观裂缝的抑制效果更好，被拔出需要消耗更多的能量．

由表6和图9可知，第3组试件L3S1.5在挠度2mm和10mm处能量吸收值分别为81.84J、562.47J，较试件L2S1.5、L0S1.5分别提升56.3%、4.0%和40.4%、57.4%．表明单掺1.5%SF的UHPC板，在正常使用极限状态内，铺设3层GFN的试件相比0层和2层试件其弯曲韧性提升显著；当超过挠度限值时，铺设GFN相比0层试件弯曲韧性提升显著，但铺设3层GFN试件其弯曲韧性较2层试件提升较小．

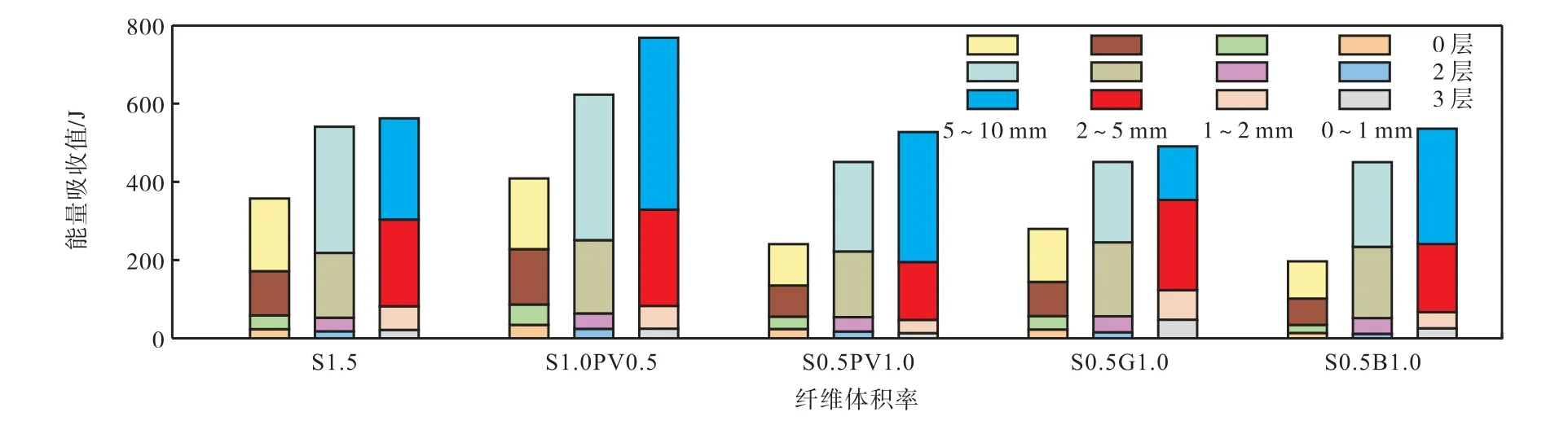
图9 不同GFN层数UHPC板能量吸收值Fig.9 Energy absorption values of UHPC slabs with different GFN layers

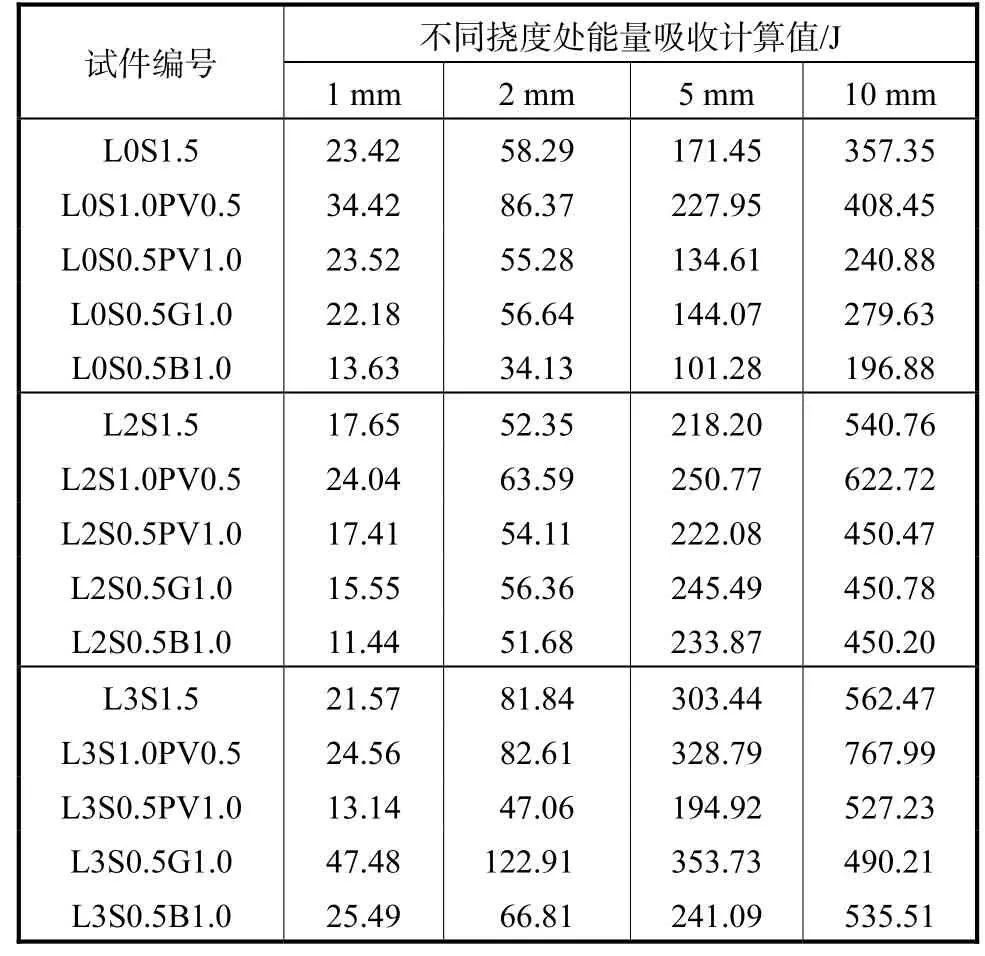
表6 不同挠度能量吸收计算值Tab.6 Calculated energy absorption values for different deflections

2.3.2 纤维网格层数对UHPC板弯曲韧性的影响

对于PVA纤维与SF混杂的UHPC板，在挠度1mm和2mm处，铺设2层和3层GFN试件的能量吸收值与0层GFN试件差异较小，在5mm和10mm处能量吸收值比0层试件增大1.5～2.0倍.表明在正常使用极限状态内，铺设GFN对PVA纤维与SF混杂的UHPC板弯曲韧性影响较小；当超过挠度限值时，GFN能充分改善UHPC板的弯曲韧性．GF或BF混杂的UHPC 板在挠度限值内，铺设2层GFN试件的能量吸收值较0层试件增幅较小，铺设3层GFN试件的能量吸收值较2层和0层试件显著增加．当超过挠度限值时，第3组试件L3S0.5G1.0、L3S0.5B1.0在挠度10mm处能量吸收值 分 别 为 490.21J、535.51J，较第 2 组 试 件L2S0.5G1.0、L2S0.5B1.0分别提升了8.7%、18.9%．

综上可知，GFN对UHPC板弯曲韧性的改善随着GFN层数增加逐渐变好，但由于层数增加使得GFN距离板中和轴越来越近，GFN受拉变形减小，因此UHPC板弯曲韧性的增幅随GFN层数的增加逐渐降低．

3 抗弯承载力计算

UHPC受弯构件截面的受压和受拉区实际应力分布图均为曲线，为了简化计算，将截面受拉、受压应力曲线图等效为矩形应力图，如图10所示．

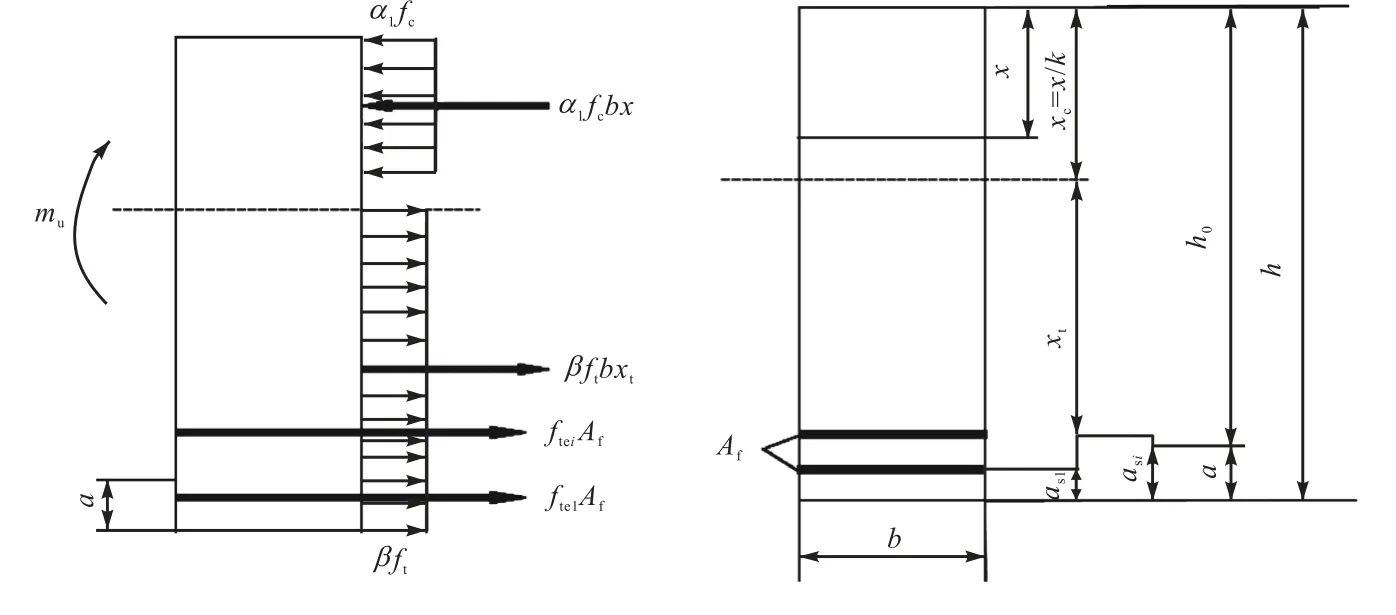
图10 双向板矩形截面受弯承载力计算图Fig.10 Calculation diagram of the bending capacity of a rectangular section of the two-way slab

混凝土受拉区等效高度计算式为

令

式中：xc为受压区高度；xt为受拉区等效矩形应力图高度；h为板的截面高度；x为受压区UHPC等效矩形应力图高度；k为受压区UHPC矩形应力图高度x与按平截面假定确定的中和轴高度xc的比值，根据文献[26]，取0.72．

根据平衡条件，轴向力计算式为

其中

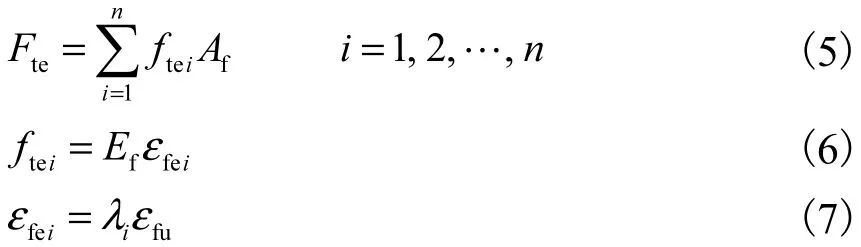
式中：fc、ft分别为UHPC轴心抗压、抗拉强度；α1、β分别为fc、ft等效应力值影响系数，分别取0.88和0.35[26]；b为板宽；Af为单层GFN截面面积；n为玻璃纤维网格层数，为避免布置时网格位于受压区，n＜6，在本试验中n为3；Fte为所有网格拉力之和；ftei为第i层网格有效应力值；Ef为GFN弹性模量；εfei为第i层网格的有效应变值；λi为第i层GFN有效利用率；εfu为GFN极限拉应变．

根据平截面假定可知，多层GFN的应变呈线性分布，即

式中asi为第i层网格到板底边缘的距离，由试验设计知as1、as2、as3分别为3.5mm、7.5mm、11.5mm．

在纤维网格破坏前，混凝土拉应变小，混凝土受压区压应变和第i层纤维网格的有效拉应变符合平截面假定，其关系式为

式中：εc为极限荷载时的混凝土受压区压应变；h0为i层网格双向板跨中截面的有效高度．

经过换算得到

受拉区纤维网格合力作用点至板底截面边缘的距离为a，其计算式为

对网格合力作用点求矩，板抗弯承载力的计算公式为

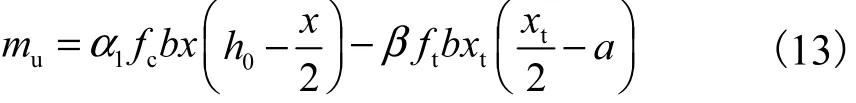
混凝土受压区高度按照下列步骤(迭代法)进行计算：先假定混凝土受压区高度xc1，然后带入式(9)计算出第1层纤维网格有效拉应变εfe1，再由力平衡式(4)计算出x1，将x1带入式(3)计算出xc2，用xc2替代xc1重复上述步骤，直至xc1和xc2误差小于1%时，所得xc2即为混凝土受压区高度．

通过计算，各UHPC板的计算结果见表7．由表7可见，随着GFN层数增加，单掺SF的UHPC板的单位宽度的理论抗弯承载力从7.24kN·m增至8.31kN·m，增长14.8%，第1层网格有效应力从2123.01MPa减至1872.87MPa，利用率从89%减至78%，各混杂纤维UHPC板具有相同的变化趋势．表明网格有效应力、利用率随GFN层数增加而逐渐减小，抗弯承载力随层数增加而增大．其中1.0%SF和0.5%PVA纤维混杂的UHPC板网格有效应力、利用率及抗弯承载力均最大，相较其他纤维种类，1.0%SF和0.5%PVA纤维混杂使GFN得到充分利用，UHPC板抗弯承载力提升最显著．另外，根据塑性铰线理论，运用虚功原理计算得出的试验弯矩me与理论抗弯承载力mu吻合良好．

4 结 论

(1) 未铺设GFN的混杂纤维UHPC板荷载-挠度曲线下降段较平缓，试件呈现多裂缝缓慢扩展的延性破坏模式，试件破坏时整体性良好；单掺1.5%SF的UHPC板较混杂纤维UHPC板在峰后持荷能力更强，延性更好．

(2) 未铺设GFN的UHPC板，当1.0%SF与0.5%PVA纤维混杂时，板的承载力最高且弯曲韧性最优；0.5%SF与1.0%BF混杂的UHPC板具有明显的变形硬化特征．

(3) 铺设GFN的UHPC板极限承载力和能量吸收值随着GFN层数的增加而增大，GFN在其中发挥了显著的增强增韧作用；纤维网格强度利用率随着层数增加而降低．

(4) 考虑GFN的纤维有效利用率，建立了GFN增强UHPC板抗弯承载力计算公式，计算值与试验值吻合良好．