矿井降温系统压力交换装置热混合过程研究

2022-03-04乔晓宇徐世昌

天津大学学报(自然科学与工程技术版) 2022年6期

王越，乔晓宇，周杰，孙政，徐世昌

(1. 天津大学化工学院，天津 300350；2. 化学工程联合国家重点实验室(天津大学)，天津 300350；3. 天津市膜科学与海水淡化技术重点实验室，天津 300350)

随着我国煤矿产业开采技术以及装备水平的提升，煤矿开采深度以8～12m/a的平均速度不断增加，矿井热害问题日益加重，必须使用机械制冷降温的方式遏制热害问题[1-2]．地面集中降温系统是在地面设置制冷站，通过循环保温管道将冷水输送至井下的方式实现工作面降温．该系统以其设备简单、制冷效率高的优势得到广泛应用[3-4]．我国矿井的平均采深已介于650～850m，冷水从制冷站到井下的静压就能达到6.5～8.5MPa甚至更高，因此需要引入降压装置对冷水进行降压从而满足工作面空冷器的压力使用要求，降压后的压力一般为2MPa[5]．

地面集中降温系统常用的高压冷水降压装置分为高低压换热器和压力交换装置两种，其中压力交换装置中压力交换的基本原理为帕斯卡定律，具体指两股不同压力的冷热水流体在直接接触的瞬间会进行压力传递，从而实现高压冷水的降压和低压热水的升压．相比于传统的高低压换热器，压力交换装置的突出优点[6-7]主要有：①冷水降压过程中温度跃升低于1℃，进入空冷器的水温低，从而保证了更好的降温效果；②当换热量固定时，直接减少了所需冷水的流量，从而降低了制冷站的制冷负荷和井下循环水泵的电机功率，节能效果显著；③压力交换装置主体为腔体管道，其结构简单的特点决定了其阻力损失较低同时便于维护等．综上所述，压力交换装置近年来在矿井降温系统中得到了广泛的应用．

目前一些地面集中降温系统中使用SIMAG公司[8-9]的三腔压力交换系统(PES)，通过水泵与制冷机的过程控制，减少了制冷机的能耗；中国煤炭科工集团重庆研究院设计了基于工控机和PLC控制单元的压力交换装置集中控制系统，同时对装置的承压部件进行了强度设计、疲劳设计和应力分布研究[10]；平煤四矿将高低压换热器更换为压力交换装置进行系统节能改造，月节约运行费用约为32.55万元，综合节能效果显著[11]．相关文献对压力交换装置的研究集中在应用效果分析和节能评价方面，缺乏冷热水直接接触进行压力交换时热混合机理方面的研究成果．

本课题组长期从事海水淡化节能装置开发，相关装置和技术已在海水淡化系统中得到验证和应用[12]，已自主研发了多套阀控式压力交换装置，其中Zhou等[13-14]对双缸阀控式压力交换装置(RS-ERD)进行了容量灵活性研究同时利用CFD模拟了切换器内部流场特征；Sun等[15]设计开发了三缸阀控式压力交换装置(TC-ERD)，通过耦合海水淡化系统运行验证了装置连续工作的稳定性．TC-ERD显著的结构特征为进行压力交换的水压缸内不设置实体活塞，即两股流体通过直接接触进行压力交换，满足海水淡化系统和矿井降温系统对压力交换装置的稳定性高、压力和流量脉动小的运行性能要求．当TC-ERD应用于海水淡化系统时，存在两股不同盐度流体的传质混合问题，影响的是海水出口的盐度；如果TC-ERD应用于矿井降温系统，存在两股不同温度流体的热混合问题，影响的是冷水出口的温升，因此可以将海水淡化领域压力交换过程中传质混合问题的研究方法延伸到矿井降温系统中．

笔者基于本课题组TC-ERD水压缸的物理模型和矿井降温系统的经验参数建立了热混合的CFD模型，进而研究了二次低压回路中热混合段的演变规律和操作参数以及结构参数对出口温升的影响，验证了该装置在矿井降温系统的适用性，对工程设计和TCERD的应用推广具有指导作用．

1 装置介绍

图1为TC-ERD在矿井降温系统的工作原理图，整个压力交换系统包含一次高压回路和二次低压回路两个循环回路．3个水压缸的两端都分别连接了一次高压回路和二次低压回路．在一次高压回路中，水在地面制冷站和三缸压力交换系统中循环，两端阀门开启时，高压冷水置换低压热水，低压热水增压并流向地面制冷站，水压缸内为高压冷水，两端阀门闭合，高压冷水泄压为低压冷水；圧在二次低回路中，水在三缸压力交换系统和末端空冷器中循环，两端阀门开启时，低压热水置换低压冷水，低压冷水流向末端空冷器，实现工作面降温．

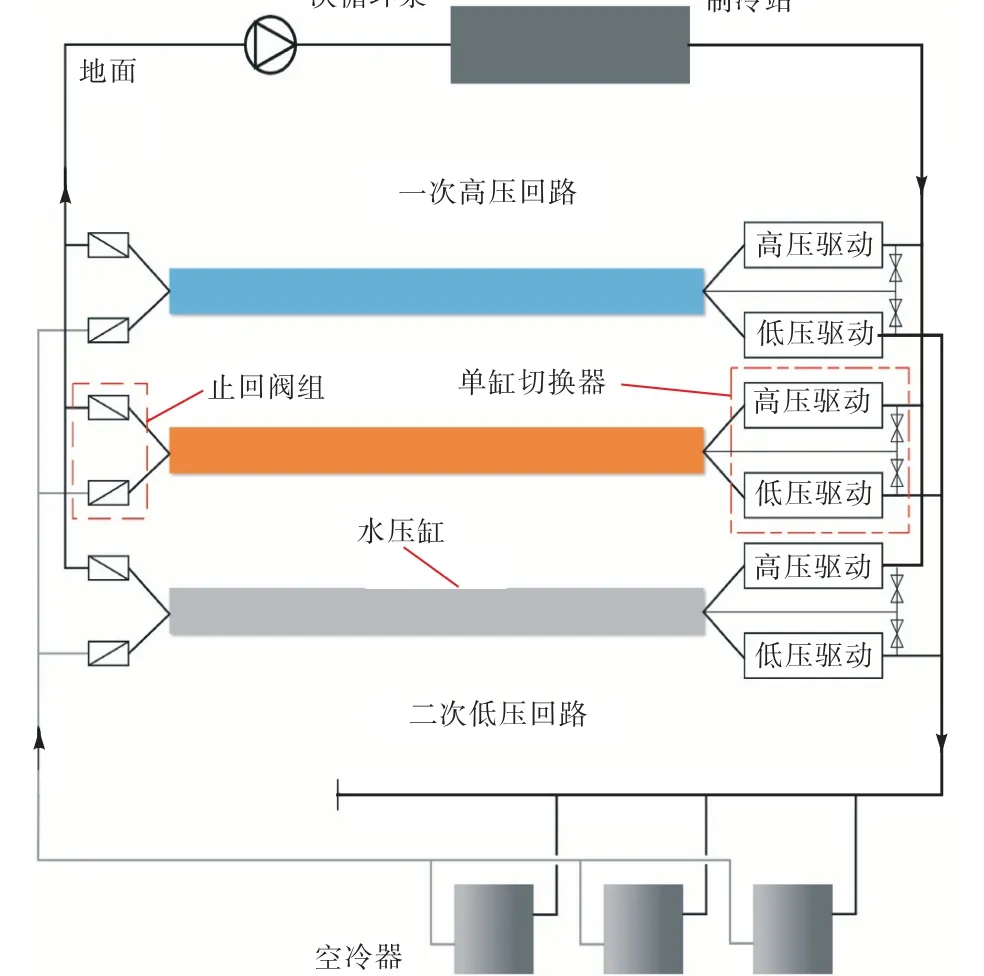
图1 TC-ERD工作原理Fig.1 Working principle of a TC-ERD

TC-ERD的关键结构包括流体切换器、水压缸和止回阀组3部分，其中流体切换器是其核心部件，每个水压缸都配置一个流体切换器组件，切换器包括两个高低水压驱动装置、两个商用止回阀以及法兰盘等连接件，水压驱动装置连接电磁阀，在一定的控制逻辑下通过控制电磁阀有序的开闭从而实现高压或低压流体周期性切换；止回阀组通过内部阀板的开闭实现流体与水压缸的连通和关闭；水压缸是进行压力交换的主要场所，3个水压缸采用“一增一泄一等待”的工作模式交替进行增泄压过程，即一个水压缸处于增压状态，一个水压缸处于泄压状态，第3个水压缸处于等待状态．当处于工作状态的水压缸即将由增压转为泄压状态或由泄压转为增压状态时，处于等待状态的水压缸便会衔接过渡到同一工作状态．这种工作模式保证了3个水压缸的工作状态呈现周期有序的切换．TC-ERD无实体活塞的结构特点和增泄压皆存在重叠的工作原理使得系统压力和流量的脉动被大大削弱，在实现压力交换功能的同时能保证装置安全稳定的运行，在矿井降温系统中具备良好的适用性．

2 数值模拟

水压缸存在连通一次高压回路或二次低压回路的两种操作工况，两个回路的热混合研究是独立的，由于二次回路中冷水出口温升直接关系到末端空冷器的进水温度，进而决定系统能耗大小和能否稳定运行，因此本文主要研究二次低压回路中低压进流热水和低压冷水的混合规律，数值模拟结果适用于二次低圧回路．根据帕斯卡定律，两股流体接触时压力会瞬间传递，因此冷热水压差对模拟结果不会产生影响，模拟中设置流场中各处压强一致，均为常压．二次低压回路中，冷水出口温升过大一方面会降低空冷器的换热效率，另一方面也会影响系统的稳定运行，因此对冷水出口温升有一定的限制，一般规定低于1℃．

2.1 物理模型

水压缸水平放置，左侧为入口，右侧为出口，初始时刻水压缸内充满静止冷水，随热水的充注从出口流出，流动为单冲程过程，通过雷诺数计算可知流入水压缸内的流体流型为湍流．

假设：

(1) 本文为热混合过程的规律探究，不考虑壁面传热的影响；

(2) 流体不可压缩，前期研究表明压力对热混合过程的影响可忽略不计．

基于以上假设得到的物理模型如图2所示．图中：Q0为水压缸内冷水初始流量，0m3/h；t0为水压缸内冷水初始温度，3℃；p0为水压缸内冷水压力；p1为热水压力，p0＝p1＝0.1MPa；Q1为热水进流流量，m3/h；t1为热水进流温度，℃；D为水压缸内径，0.13m；L为水压缸长度，6m．

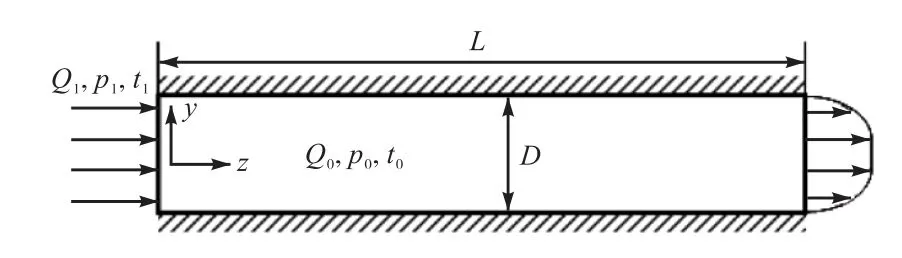
图2 水压缸物理模型Fig.2 Physical model of a cylinder

2.2 网格划分

使用SolidWorks进行三维建模之后，导入Pointwise软件进行空间离散．由于水压缸的结构比较规则，划分为六面体网格．网格质量对圆周节点数量敏感度较高，周向节点距离应较小；网格质量对轴向节点敏感度较低，轴向节点距离可以较大，网格划分模型如图3所示．

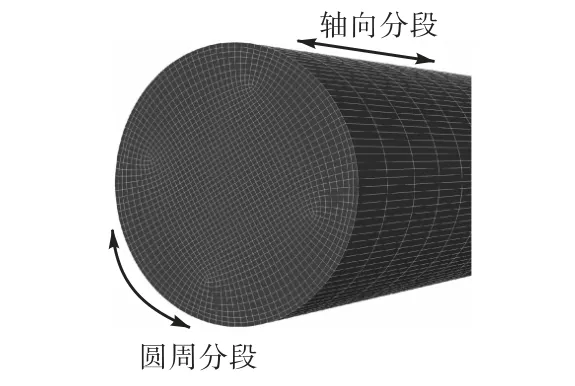
图3 水压缸网格划分模型Fig.3 Meshing model of a cylinder

2.3 控制方程

根据本装置的物理模型和模拟工况，选择并化简得到适用于水压缸的各类控制方程表达式[16]．

1) 连续性方程

流体流动遵循基本的质量守恒定律，对于不可压缩流体，化简后的连续性方程为

式中ux、uy、uz分别为x、y、z方向的流速．

2) 雷诺平均方程

对运动方程进行雷诺转换从而获得湍流流动时物理量的时均值所满足的方程，转换后的雷诺平均方程为

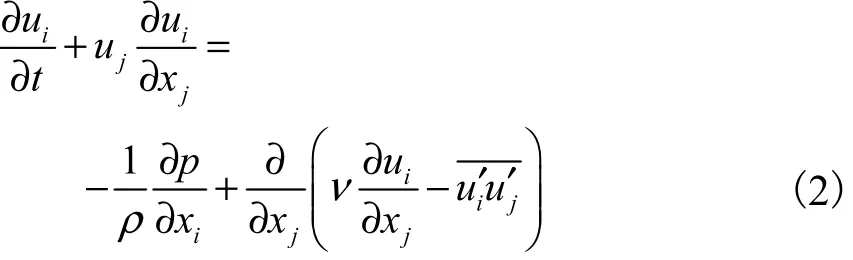
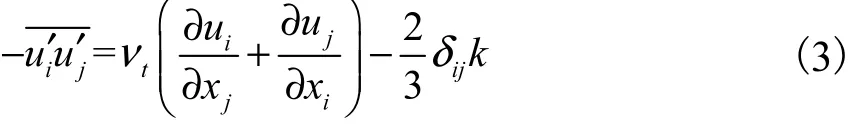
湍流黏性系数tv由湍动能k和耗散率ε的函数定义：

式中：ρ为流体密度；t为时间；p为压强；νt为运动黏度；u′i、u′j为脉动速度；ijδ为克罗内克(Kronecker)符号；μC为模型常量，数值取0.09．

3) 湍动能k方程

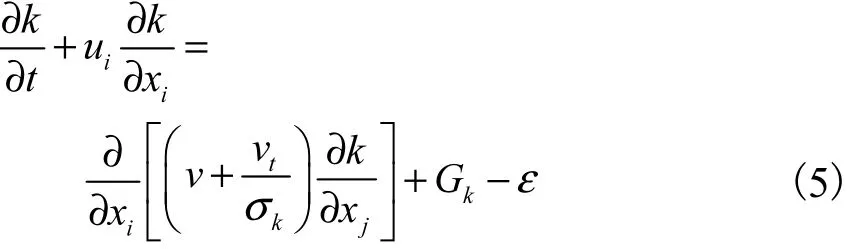
式中：kG为湍动能k的产生项为湍动能k对应的湍流Prandtl数值，取1.0．

4) 耗散率ε方程

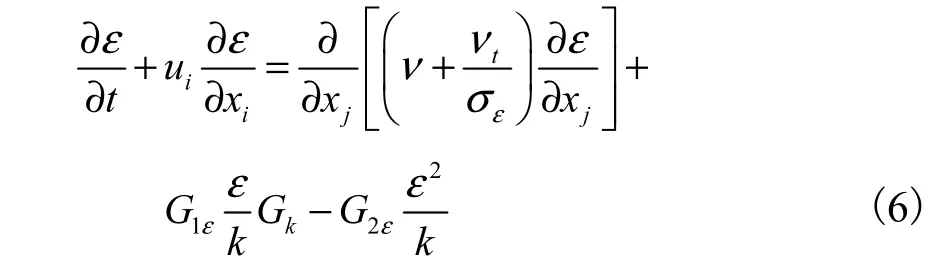
5) 能量方程

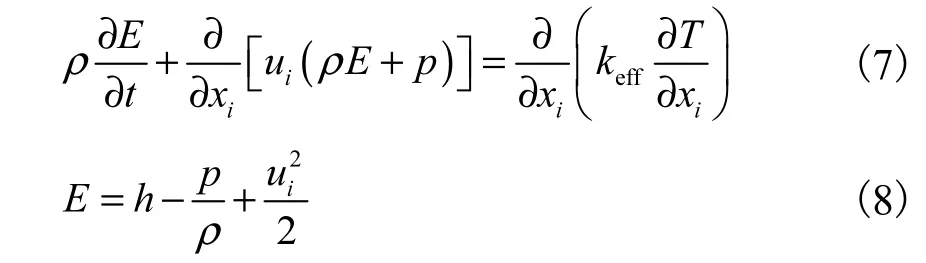
式中：keff为有效热传导系数，其中kt为湍流热传导系数，根据使用的湍流模型来定义；T为温度；E为单位质量流体的总能量；h为显焓．

上述方程构成了求解水压缸内冷热水混合流场规律的基础数学模型，根据实际工况设置边界条件迭代计算至收敛即可得到全流场定解．

2.4 边界条件和参数设置

使用基于有限体积算法的ANSYS Fluent19.2进行数值计算，设置速度入口、压力出口和无滑移壁面的边界条件．湍流模型为标准k-ε模型，开启能量方程，压力基求解器使用SIMPLE压力与速度耦合算法．瞬态模拟的时间步长设置为0.001s，迭代残差降至10-5以下作为收敛的基本判据．设置壁面绝热，采用标准壁面函数进行近壁面处理，通过优化第1层网格节点位置使无量纲壁面距离y+稳定在30～300范围内[17]，从而保证壁面函数结果可靠．

在分析CFD模拟结果之前，首先需要进行网格无关性验证，固定圆周节点距离为3.5mm以保证圆形截面网格精度，轴向节点距离从12～50mm范围内变化得到5种网格数(表1)．定义中轴线0m位置为进口，6m位置为出口．如图4所示，选取进流时间为5s时中轴线2～4.5m位置的温度分布进行网格无关性验证．同时绘制两个图像，每个图像都包含网格数为375115的温度分布曲线，可以看到5种网格数中轴线温度分布基本重合，网格数量为224315和280865的模拟曲线在温度拐点处存在细微的误差．综合考虑模拟精度和占用内存，最终确定网格总数为375115，此时网格质量评价的关键指标网格最小正交质量为0.94，最小正交质量的数值范围为0～1，最差为0，最好为1，表明本文网格正交性较好，网格划分质量高．

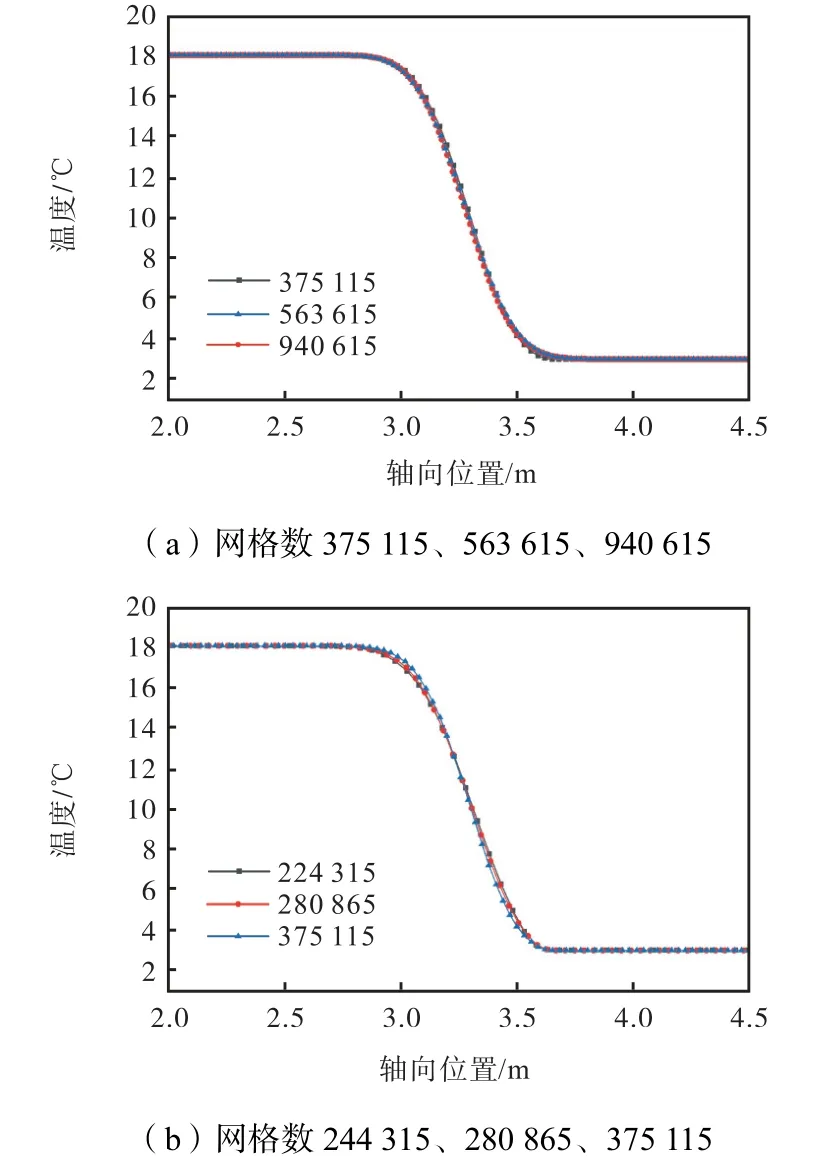
图4 5s时中轴线温度分布Fig.4 Temperature distribution on the central axis at 5s

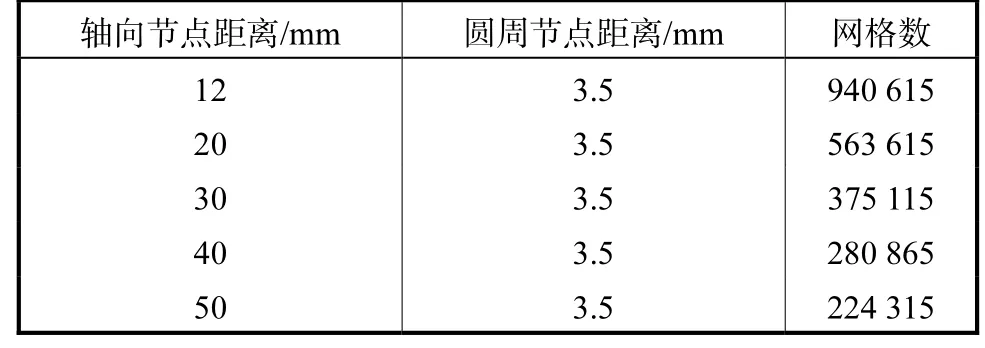
表1 5种网格数量选择Tab.1 Five grid number options

3 结果分析与讨论

3.1 温度混合段演变规律

规定热水进流流量Q1为30m3/h，t0为3℃，t1为18℃，D为0.13m，L为6m，图5表示水压缸在不同进流时间节点的中心截面温度云图，左侧红色部分为热水进流，蓝色部分表示水压缸内的冷水，两流体之间颜色变化的区域表示冷热水的混合段．结果表明：随着进流时间的增加，热水进流长度不断增加，水压缸内冷水在热水的推动下从右侧排出水压缸，混合段长度也不断增加，混合段锋面逐渐向出口位置靠近；温度场表现出随速度场同步发展的特性，首先在0.25～1s时间内，温度混合段锋面基本为平直型，之后混合段锋面不断发展演变，这是由于初始流场处于静止状态，产生了入口效应，即热水刚开始进流时湍流边界层处于初始形成阶段，随着热水进流时间的不断增加，湍流边界层不断发展直至充分发展；在8.75s温度混合界面前峰已到达出口位置，此时出口的瞬时温升为1℃．

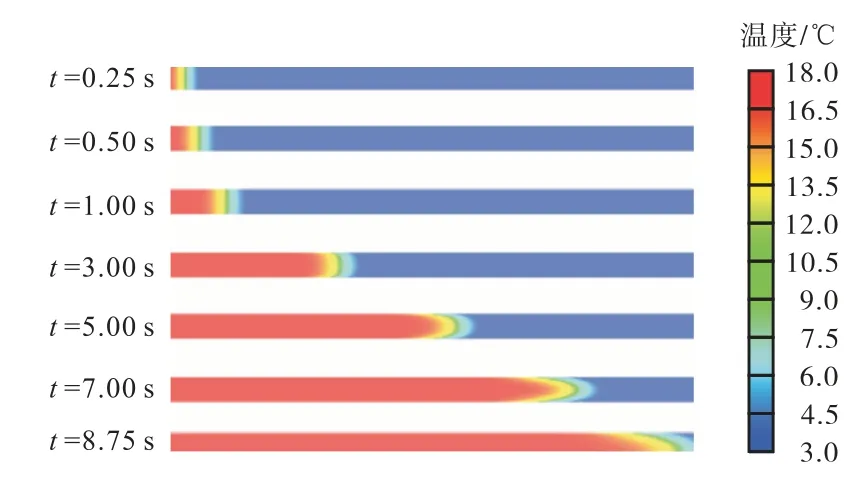
图5 不同进流时间水压缸温度云图Fig.5 Cylinder temperature field at different inlet times

不同时刻沿轴向过流截面的面平均温度分布如图6所示，图中轴向位置的0m处为进口，沿x轴正向为进流方向，6m处为出口，取温度介于3℃和18℃的长度作为混合段长度，1s、3s、5s和7s时刻的混合段长度分别表示为l1、l2、l3和l4．从图6(a)中可以看出随着进流时间从1s增加到7s，不同时刻混合段呈现近平行迁移的规律，从图6(b)也可以观察到混合段长度从0.8m逐渐增加到1.6m，这一变化趋势与图6温度云图所反映的规律是一致的．

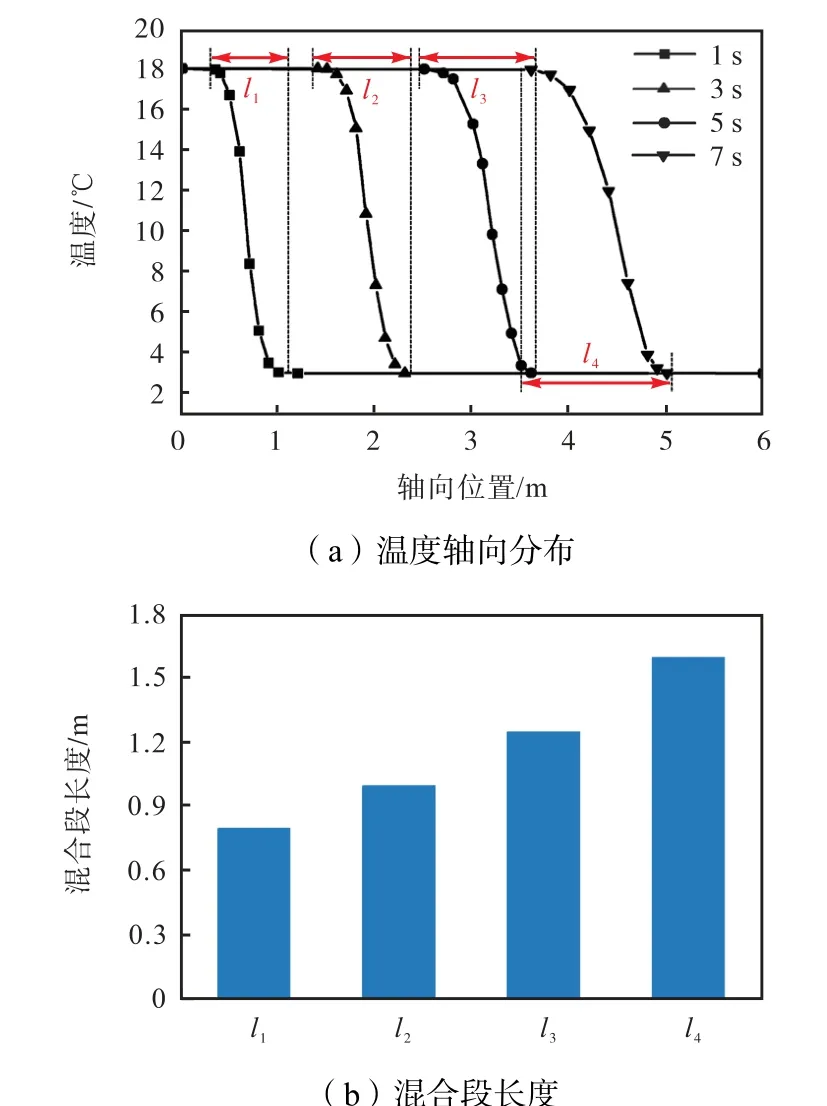
图6 不同进流时间水压缸温度轴向分布Fig.6 Axial distribution diagram of cylinder temperature at different inlet times

图7表示水压缸不同热水进流流量Q1下混合段长度随进流时间的演变曲线，经模拟验证水压缸内流场各过流截面平均流速始终保持与进口流速相同，定义进流时间与进口流速的乘积为进流长度．从图7中可以看出，当Q1一定时，例如30m3/h时，首先在0～1s时间内快速形成0.8m的混合段，这主要是入口效应引起的，之后混合段随时间呈现较为规则的递增趋势，在8s时达到1.7m，其他流量的曲线也呈现相似的变化规律．当Q1从20m3/h增至50m3/h时，进流时间为1s时形成的混合段长度非常接近，此时流量越大意味着进流长度越大，所以混合段所占进流长度的比例越小，表明大流量克服入口效应的效果更好；在1～5s范围内，进流时间相同时，流量越大，混合段长度越长；在5s之后只统计了混合段没有排出水压缸时长度随时间变化规律，因此流量越小统计的进流时间越长，20m3/h进流时间能达到12s．进流时间相同时，流量越大，意味着混合段长度以及进流长度都越大，当水压缸结构尺寸固定时，进流流量对出口温升的的影响会在第3.2节进一步讨论．

阀控式压力交换装置通过阀门开闭控制冷热流体交替流入、流出或静止于水压缸，这种非连续的交变流表现出了区别于定常流的速度分布特性，温度云图和温度混合段长度随时间的演变规律体现了速度场对热混合过程有直接的影响，因此需要研究水压缸内速度分布随时间的变化规律来验证热混合段的发展规律．经过模拟验证，垂直于轴线的过流截面沿不同位置的半径上具有一致的径向速度分布规律，定义无量纲的径向位置r/R，其中管道中心处和管壁的无量纲径向位置分别为0和1，如图8所示．

工程上常采用Nikurades法[18]对适用于本装置模型的光滑或水力光滑圆管内完全发展湍流速度分布进行理论计算，速度u的分布计算式为式中：u∗为摩擦速度，m/s；sτ为壁面剪切力；y为径向距壁面的距离；υ为运动黏度；Δp为流体压降；L为管长．

图9表示Q1为30m3/h、D为0.13m、L为6m时，以出口截面为例的速度分布在不同进流时间的特征规律．结果表明，随着进流时间的增加，模拟得到的速度分布与采用式(9)～(11)计算得到的充分发展的理论速度分布之间的差值越来越小．由于初始流场静止，进流前1s速度分布基本呈现与进口时几乎一致的没有发展的均匀速度边界条件，在温度云图上表现为平直型层状的热混合界面，这种入口效应大大强化了热混合过程，因此前1s的热混合段长度表现出快速增长特性．1s、3s、5s、7s和8.75s时刻管中心最大流速分别为0.65m/s、0.67m/s、0.70m/s、0.73m/s和0.74m/s，最大流速逐渐增大且在7s之后趋于稳定并接近0.75m/s这一充分发展的理论值，在温度云图上体现为热混合段的峰状界面不断拉长，同时混合段长度随时间呈现近线性的增长规律．综合来讲，区别于速度分布不随时间改变的稳态湍流，以上规律体现了水压缸内流体交变运行带来的速度场和温度场随时间同步发展的特性．

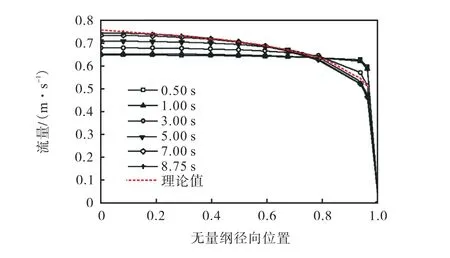
图9 不同进流时间下速度分布规律Fig.9 Distribution law of velocity at different inlet times

3.2 热水进流流量对出口温升的影响

冷热流体的混合段必然会占据一定的水压缸体积，由于冷水出口温升的限制，混合段不可能全部排出水压缸，为了方便进行单变量研究，引入容积利用率的概念，定义为最大进流长度除以水压缸长度，用来评价水压缸全容积的利用效率．在满足出口温升这一工艺参数要求的前提下容积利用率大于90%即可被认为装置利用效果较好，定义式如下：

式中：lmax为最大进流长度，m；L为水压缸长度，m．

图10表示t0为3℃、t1为18℃、D为0.13m、L为6m时，不同的热水进流流量Q1对应的水压缸容积利用率η与出口温升∆t的对应关系．当Q1一定时，例如20m3/h的曲线，随着出口温升的增加，容积利用率呈正增长的趋势，这是由进流长度的增加导致的，在最大允许出口温升1℃处，对应的最大容积利用率是91.13%，其他热水进流流量下曲线也呈相似的变化规律．当∆t一定时，例如在最大允许出口温升1℃处，随着热水进流流量的增大，容积利用率呈略微增加的趋势，20～50m3/h流量对应的容积利用率分别为91.13%、91.58%、91.91%、92.17%，流量增大了1.5倍，容积利用率只增加了1.04%．

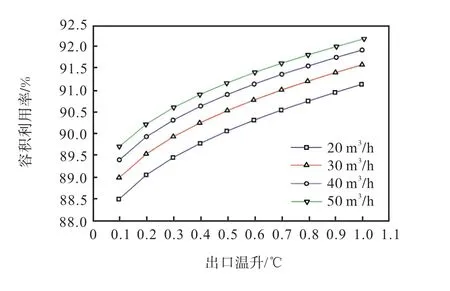
图10 不同流量下出口温升与容积利用率对应关系Fig.10 Relationship between the outlet temperature rise and the volume utilization ratio at different inlet flows

尽管流量增大带来了容积利用率的小幅度增加，但会降低装置循环周期从而增加起控制流体切换作用的电磁阀的切换频率，过高的切换频率不利于装置的稳定运行，也会降低电磁阀的运行寿命．不同热水进流流量下循环周期和切换频率如表2所示，根据“一增一泄一等待”的工作模式，循环周期按照最大允许出口温升1℃对应的最大进流时间的3倍计算，在一个循环周期内，根据控制逻辑单个电磁阀共完成两次工作位的切换，从而计算得到切换频率．电磁阀的总切换频次按工程经验取50万次，按照本装置的水压缸结构尺寸模型，可以根据切换频率得到连续工作时电磁阀的维护周期，如果需要进行流量调整，工程设计中应结合冷量需求和合理的切换频率及维护周期要求综合决定流量调整范围．

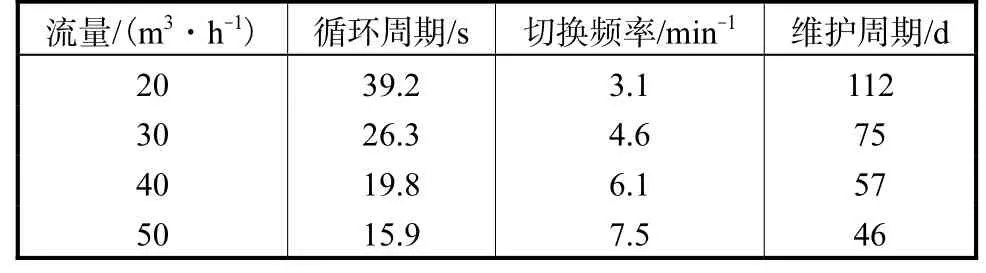
表2 不同流量对应切换频率Tab.2 Switching frequency at different inlet flows

3.3 冷热流体温差对出口温升的影响

工业实际中，一次回路冷水进口温度一般为3℃，但各矿井底部的需冷量不同，这就导致了二次回路中热水进流温度不同．因此，有必要研究冷热水温差对热混合的影响．

图11表示t0为3℃、Q1为30m3/h、D为0.13m、L为6m时，不同冷热水温差(t1－t0)对应的水压缸容积利用率η与出口温升∆t的对应关系．结果表明：各曲线同时表现出随着出口温升的增加，容积利用率正增长的趋势，同时曲线之间的间距随出口温升的增加由密变疏，表明冷热水温差对容积利用率的影响程度也不断增加．当∆t一定时，例如在最大允许出口温升1℃处，冷热水温差越小，容积利用率越高，当冷热水温差从18℃降低到12℃时，容积利用率从91.28%增加到91.98%，增幅为0.7%．冷热水温差对热混合过程的影响主要是由于流体各部分互相接触，温差增大，热传递的温度梯度增大，从而加快了热传递的速率．

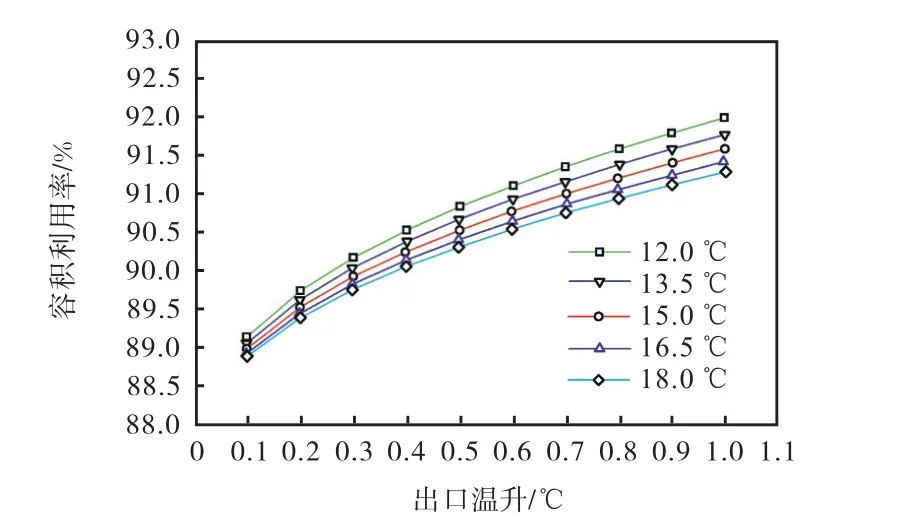
图11 不同冷热水温差时出口温升与容积利用率对应关系Fig.11 Relationship between the outlet temperature rise and the volume utilization ratio at different temperature differences between hot and cold water

3.4 结构尺寸对出口温升影响探究

3.4.1 水压缸长度对出口温升的影响

图12表示Q1为30m3/h、t0为3℃、t1为18℃、D为0.13m时，水压缸长度L从6m增加到18m容积利用率η与出口温升∆t的对应关系．结果表明：当∆t一定时，随着水压缸长度的增大，容积利用率呈增加趋势，在最大允许出口温升1℃处，6～18m长度对应的容积利用率分别为91.58%、92.15%、92.96%、93.42%和93.88%，长度增大了2倍，容积利用率增加了2.3%，数据表明增大水压缸长度对增加容积利用率有较好的效果．

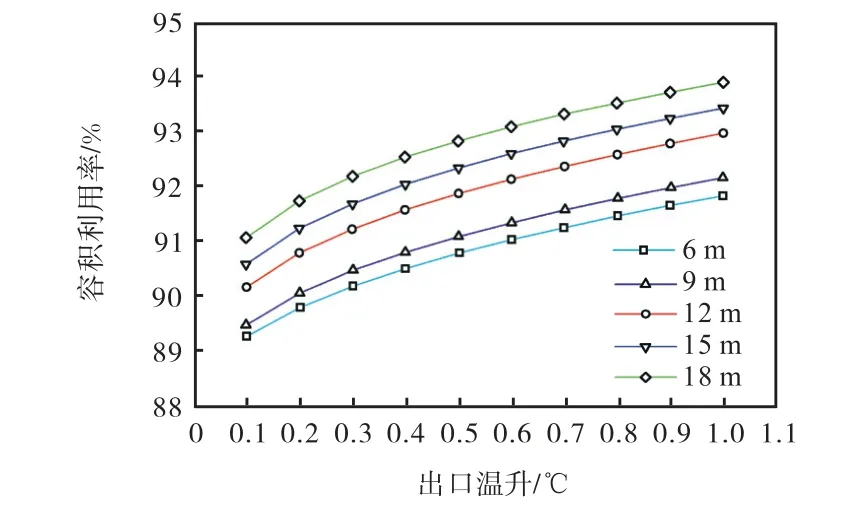
图12 不同水压缸长度下出口温升与容积利用率对应关系Fig.12 Relationship between the outlet temperature rise and the volume utilization ratio at different lengths of the cylinder

表3表示Q1为30m3/h、D为0.13m、电磁阀的总切换频次为50万次且最大允许出口温升1℃时不同长度水压缸对应的切换频率和维护周期．结果表明：随着长度从6m增加到18m，对应的切换频率从4.6min-1降低到1.5min-1，二者基本满足负线性相关关系，切换频率降低意味着电磁阀的维护周期大大增加，长度为18m时维护周期可以达到231天．一般来说矿井的维护周期为半年以上，因此在工程实践中水压缸常采用较大的长度，一方面能够提高容积利用率，另一方面也显著降低了电磁阀的切换频率从而延长维护周期，当然同时也会造成设备投资成本的增加，目前工程上已知的水压缸长度能达到38m及以上，对应的维护周期能达到1年以上．

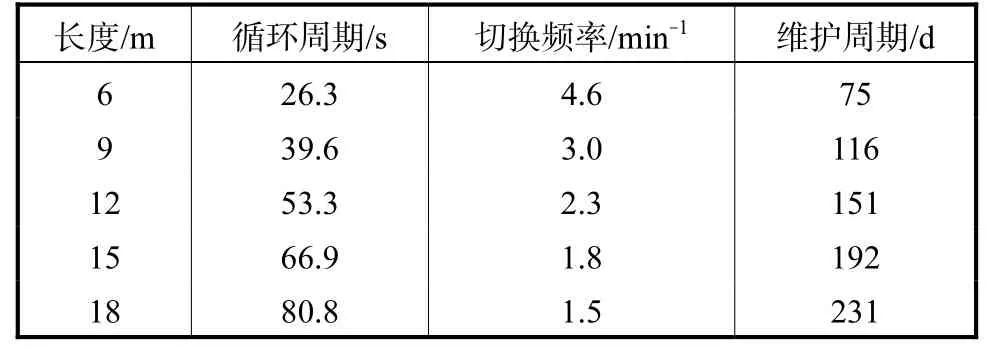
表3 不同水压缸长度对应切换频率Tab.3 Switching frequency at different lengths of the cylinder

3.4.2 水压缸内径对出口温升的影响

水压缸内径对出口温升的影响分两种情况讨论，第1种是在缸体内流速恒定条件下分析水压缸内径对出口温升的影响规律，第2种是在缸体内流量恒定条件下分析水压缸内径对出口温升的影响规律．

图13表示t0为3℃、t1为18℃、L为6m时，分别选取本装置常运行的0.42m/s、0.63m/s、0.84m/s 3种流速，研究了在流场基本充分发展的4s时刻水压缸混合段长度随内径D的变化规律．结果表明：当流速一定时，例如0.42m/s时，随着内径从100mm增加到250mm，混合段长度从0.9m增加到1.55m，基本呈线性的正增长趋势；当内径一定时，流速越大，混合段长度越大．综合来讲，当进流热水速度、密度和黏度一定时，水压缸内径增大会使雷诺数增加，雷诺数的增加意味着湍流的剧烈程度增大，从而加剧了热混合导致混合段长度的增加，这类似于增加热水进流流量的效果．

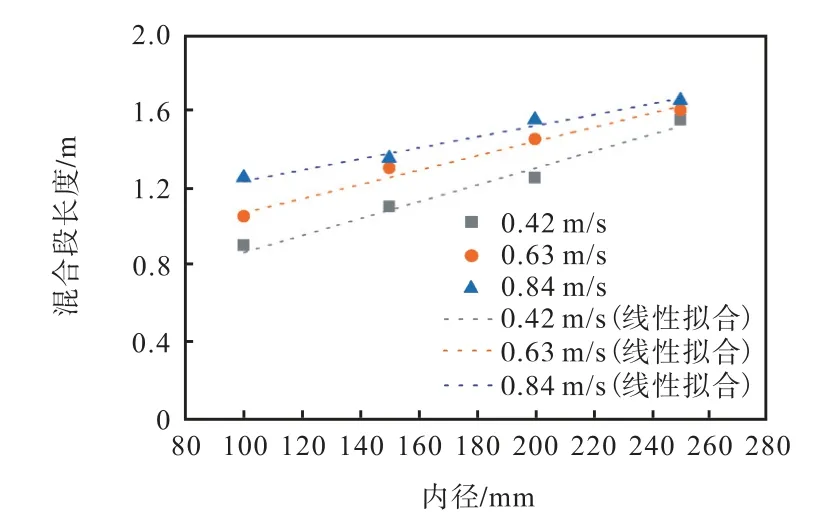
图13 固定流速下混合段长度随内径的变化Fig.13 Variation of the mixing section length with the diameter at a fixed velocity

图14表示在第1种情况下，流速固定为0.63m/s时，不同水压缸内径出口温升∆t与容积利用率η的对应关系．结果表明：当内径一定时，各曲线同时表现出随着出口温升的增加容积利用率正增长的趋势，4条曲线整体由疏变密，表明内径对容积利用率的影响越来越小；内径为100mm和150mm时两条曲线几乎重合，表明在满足出口温升的要求时二者的容积利用率非常接近．当出口温升一定时，随着内径的减小，容积利用率逐渐增大，在最大允许出口温升1℃处，内径从250mm减小到100mm，对应的容积利用率从91.43%增加到91.67%，增幅仅为0.24%，整体来说流速一定时，改变水压缸内径这一结构尺寸对出口温升的影响没有改变水压缸长度这么明显．

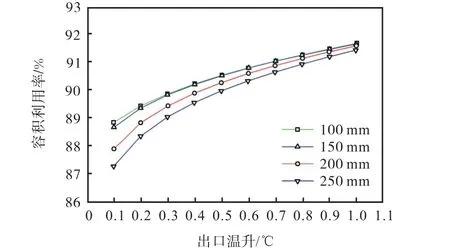
图14 0.63m/s流速时不同内径下出口温升与容积利用率对应关系Fig.14 Relationship between the outlet temperature rise and the volume utilization ratio at different diameters and a velocity of 0.63m/s

图15表示在第2种情况下，流量固定为30m3/h时，不同水压缸内径出口温升∆t与容积利用率η的对应关系，其中根据30m3/h的流量和内径换算得到的流速列在表4中．图中曲线表明，当∆t一定时，随着内径的减小，容积利用率呈增加趋势，在最大允许出口温升1℃处，内径从250mm减小到100mm，对应的容积利用率从89.33%增加到92.17%，增幅为2.84%，这主要是由于内径越大，由30m3/h的流量换算得到的水压缸内流速越小，250mm时流速仅为0.17m/s，导致总的进流时间过大，混合段长度发展的时间也过大，影响了满足出口温升要求时的装置利用效果．因此，当装置的设计流量固定时，需要对水压缸内径有一个范围要求，根据流量核算确保水压缸流速适宜，从而使容积利用率保持较高的水平．可以看出当设计流量为30m3/h时，在本文列举的4个例子中，内径在100～150mm范围内、流速介于0.47～1.06m/s，出口温差介于0.5～1℃时，容积利用率能达到90%及以上的较高水平，可以为工程设计提供参考．

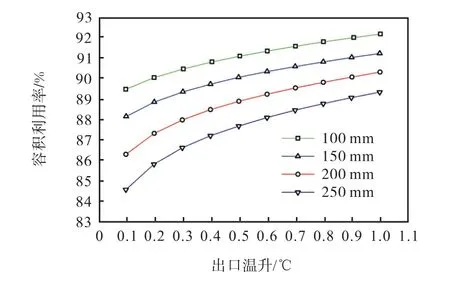
图15 30m3/h流量时不同内径下出口温升与容积利用率对应关系Fig.15 Relationship between the outlet temperature rise and the volume utilization ratio at different diameters and a flow of 30m3/h