Python在RLC串联谐振实验数据处理中的应用

赵文来，杨俊秀，陈秋妹

(浙江理工大学 信息学院，浙江 杭州 310018)

RLC串联谐振电路是电学实验内容之一，旨在加强对串联谐振电路的谐振条件，及阻抗、电流、电压特点的理解[1]。对谐振现象的研究具有一定的实际意义，一方面谐振现象广泛应用于电子技术中实现选频及滤波，另一方面在电力系统中发生谐振却需要避免或抑制[2]。利用Python的第三方机器学习库Scikit-learn来处理RLC串联谐振实验数据，并通过matplotlib库实现数据及其分析结果的可视化[3]。

1 Python工具

Python是面向对象的高级程序语言，其风格简洁，库类多样，且采用开源，具有丰富三方库和开源软件包接口，成为应用于科学计算、数据库、网络工程、GUI设计等众多领域的高级语言。

实验数据处理采用了Python的numpy，Scikit-learn和Matplotlib等库。Numpy是数值计算库，提供快速的数组矩阵运算，将RLC串联谐振实验测试数据通过相应函数转化为数组；Scikit-learn是Python的机器学习库，是用于数据挖掘、数据分析的工具，通过数据训练，实现数据的拟合回归预测、聚类、模型选取等复杂算法，采用其中的一元线性回归模型来完成实验数据的拟合；Matplotlib是Python二维画图库，可以简洁地画出折线，柱状，散点等二维图像，实现实验数据的可视化[4]。

2 原理及均方误差回归损失

2.1 实验原理

图1 RLC串联谐振实验电路原理图

其中，电路谐振时，回路电流I为：

(1)

任意频率时，回路电流I为：

(2)

回路品质因数Q为：

(3)

归一化电流为：

(4)

幅频特性表现为：

(5)

实际测量时，通常测量不同频率下的电阻电压、电感电压和电容电压，经计算得回路电流有效值，绘制出归一化电流频率特性曲线[7-10]。

2.2 均方误差回归损失

“损失函数”是机器学习优化中至关重要的一部分，机器学习中的算法都需要最大化或最小化一个函数，被称为“目标函数”。一般把最小化的一类函数，称为“损失函数”。它能根据预测结果，衡量出模型预测能力的好坏。在实际应用中，选取损失函数会受到诸多因素的制约，比如是否有异常值、机器学习算法的选择、梯度下降的时间复杂度、求导的难易程度以及预测值的置信度等等[11]。

最常用的损失函数是均方误差MSE，定义如下：

(6)

3 测试数据处理分析

3.1 配置软件环境

本方法在Win7操作系统上实现，基于Python3.6版本，并导入Python第三方软件库工具pip安装numpy，matplotlib，scikit-learn等库。

3.2 拟合曲线实现框图

首先录入RLC串联谐振实验测试数据，再利用numpy进行数据预处理，调用scikit-learn建立一元多阶线性回归模型并求解，利用数据训练及机器学习，最后通过均分误差回归损失分析判定模型最佳阶数，并进行可视化输出。实验框图如图2所示[3]。

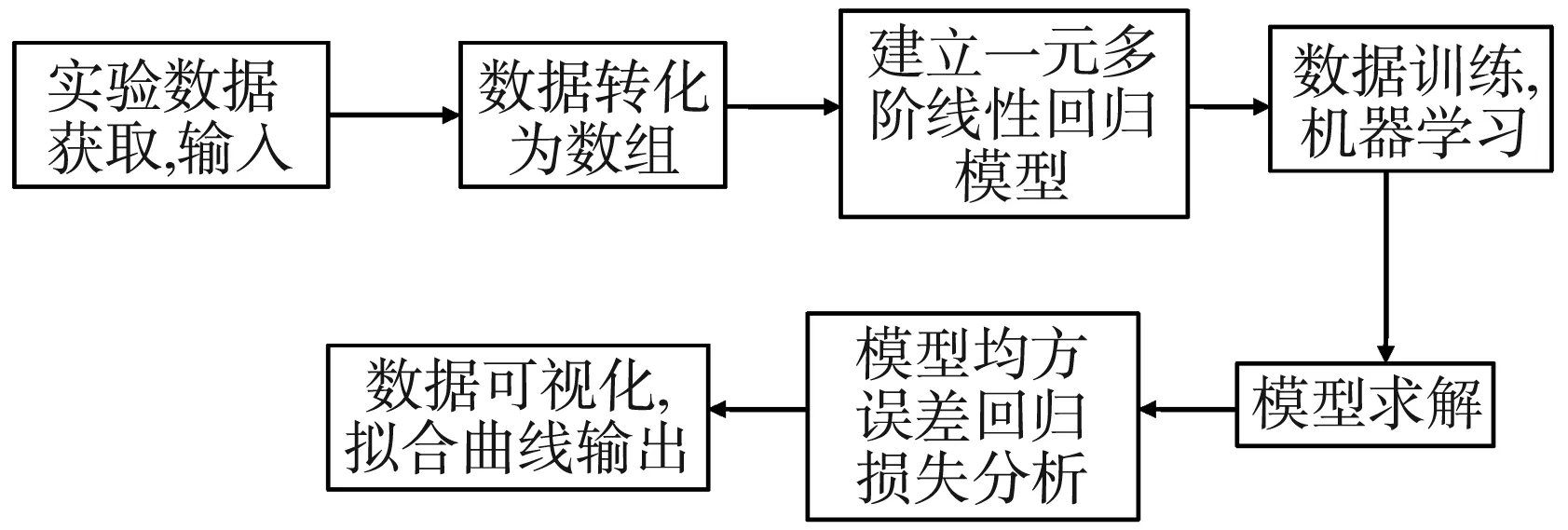
图2 拟合曲线实现框图

3.3 代码实现

(1)导入第三方库文件：

import numpy as np

import matplotlib.pyplot as plt

from sklearn.preprocessing import Polynomial Features

from sklearn.linear_model import Linear Regression,Perceptron

from sklearn.metrics import mean_squared_error,r2_score

from sklearn.model_selection import train_test_split

mpl.rcParams[′font.sans-serif′]=[’simHei′]

(2)输入数据：基于numpy的数组array()函数把数据转化成行向量，再结合reshape()函数把行向量转化为列向量。

X1=[]

Y1=[]

X=np.array([]).reshape(-1，1)

y=np.array([]).reshape(-1，1)

(3)数据拟合，机器学习：利用numpy的polyfit()函数进行数据拟合，及polyld()函数进行机器学习。

coefn=np.polyfit(x,y，n)

poly_fitn=np.poly1d(coefn)

(4)画图，利用matplotlib的plot()函数，实现数据拟合曲线可视化。

plt.scatter(X1，y1，color=′black′，′g:′,label="五阶，R=1K欧")

plt.xlabel("频率(KHz)")

plt.ylabel("归一化电流")

plt.legend(loc=2)

plt.show()

(5)数据分割及最优判断[12,13]：

x_train，x_test，y_train，y_test=train_test_split(X，y，test_size=0.3)

rmses=[]

degrees=np.arange(1，10)

min_rmse，min_deg,score=1e10，0，0

for deg in degrees:

poly=PolynomialFeatures(degree=deg，include_bias=False)

x_train_poly=poly.fit_transform(x_train)

poly_reg=LinearRegression()

poly_reg.fit(x_train_poly，y_train)

x_test_poly=poly.fit_transform(x_test)

y_test_pred=poly_reg.predict(x_test_poly)

poly_rmse=np.sqrt(mean_squared_error(y_test，y_test_pred))

rmses.append(poly_rmse)

r2score=r2_score(y_test，y_test_pred)

if min_rmse > poly_rmse:

min_rmse=poly_rmse

min_deg=deg

score=r2score

print(′degree=%s，RMSE=%.2f，r2_score=%.2f′ % (deg，poly_rmse,r2score))

fig=plt.figure()

ax=fig.add_subplot(111)

ax.plot(degrees，rmses)

ax.set_yscale(′log′)

ax.set_xlabel(′Degree′)

ax.set_ylabel(′RMSE′)

ax.set_title(′Best degree=%s，RMSE=%.2f，r2_score=%.2f′ %(min_deg，min_rmse,score))

plt.show()

4 实验结果

当R=330 Ω时，某生测试的2组实验数据见表1、表2所示。

表1 RLC实验数据第一组(R=330 Ω)

表2 RLC实验数据第二组(R=330 Ω)

代入程序，对应数据二阶、三阶、及高阶拟合结果如图3、图4所示。

频率/kHz

频率/kHz

第一组数据均方误差回归损失决定系数与阶数的关系曲线如图5所示[12,13]。

频率/kHz

由上图5可知，R=330 Ω时均方误差回归损失第一组数据在阶数为6时最佳，拟合决定系数为0.59，对应的六阶拟合曲线如图6所示。

频率/kHz

第二组数据均方误差回归损失决定系数与阶数的关系曲线如图7所示。

由上图7可知，R=330 Ω时均方误差回归损失第二组数据在阶数为4时最佳，且决定系数为0.92，大于第一组数据0.59，可见第二组数据更精确。利用均分误差回归与阶数的对应，比较拟合曲线的大致走势即可评估测试数据的优劣，决定系数越接近1越优[11]。

频率/kHz

当R=1 KΩ时，测得的2组实验数据见表3、表4所示。

表3 RLC实验数据第一组(R=1 KΩ)

表4 RLC实验数据第二组(R=1 KΩ)

对应数据二阶、三阶、及高阶拟合结果如图8、图9所示。

频率/kHz

频率/kHz

第一组数据均方误差回归损失决定系数与阶数的关系曲线如图10所示。

频率/kHz

由上图10可知，均方误差回归损失在阶数为6时最佳，决定系数为0.91，对应的六阶拟合曲线如图11所示。

频率/kHz

不同R的情形下比较第二组测试数据，对归一化电流幅频特性曲线的影响，如下图12所示。

频率/kHz

由图12可清晰观察谐振电阻R对曲线的影响，及通频带的变化情况。一方面验证测试数据的质量，同时增加对参数及曲线的感性认识。

5 结 语

借助Python语言，基于库函数的一元线性回归模型对RLC实验数据进行了二阶、三阶等曲线拟合，绘制了各拟合曲线并计算均方误差回归损失决定系数，实现了实验数据的可视化分析[4]。可见Python语言灵活方便且资源丰富，避免了学生手动计算耗时长，易出错，且不直观的弊端，学生可根据曲线自我判断测试数据的质量，实验教师通过实验数据的可视化曲线及数据分析结果，便于实验报告中数据处理部分的批改，有效提高实验教学质量。