小型无人直升机自转建模与控制策略研究

屈天祥，滕 飞，傅春啸，雍 和，盛守照

(南京航空航天大学自动化学院，江苏 南京210016)

0 引言

直升机自转飞行是当直升机发生主旋翼动力失效时，一种利用从下而上流经主旋翼的气流提供动力的不正常降落飞行状态。动力失效后，自转飞行是实现直升机安全着陆的唯一手段。

直升机是复杂的高阶非线性系统，目前，针对直升机的动力学建模主要采用第一原理建模[1-2]、系统辨识建模[3-4]以及两者结合[5]的方法。然而针对小型无人直升机的自转建模主要为系统辨识建模[6-7]，因此，研究基于第一原理建模的小型无人直升机动力学建模具有重要的研究意义。

本文以小型无人直升机Align 760X为研究对象，建立了较为完整的无人直升机自转动力学模型，根据直升机自转过程中下降速度的变化情况，将直升机自转飞行过程分为加速下降、稳定下降和减速着陆3个阶段，并进行了直升机自转飞行控制策略的设计，仿真实现了直升机自转飞行的安全着陆。

1 直升机自转模型

1.1 坐标系定义

a.地面坐标系。

固连于地面的惯性坐标系，与机体坐标系初始时刻重合。

b.机体坐标系ObXbYbZb。

机体坐标系与机体固连，原点Ob为直升机重心，纵轴ObXb位于直升机纵向对称平面内指向机头方向。竖轴ObZb位于直升机对称平面内，与桨毂轴平行，向下为正；横轴ObYb根据右手法则确定。

1.2 主旋翼及尾桨模型

主旋翼的拉力系数和功耗系数采用文献[8]中的形式，即

(1)

主旋翼的拉力和功耗可以表示为

(2)

其中，拉力系数CT,mr可通过叶素法[9]近似计算得到；功耗系数CP,mr的计算式为

(3)

σ为桨叶升力面积和桨盘面积的比值；cd为主旋翼翼型阻力系数；μ为旋翼前进比；λ为旋翼入流比。

综上所述，主旋翼产生的力与力矩在机体坐标系中的计算式为：

(4)

(5)

Hmr为主旋翼桨毂在直升机重心上方的位置；as、bs为主旋翼桨叶挥舞角。

与主桨拉力Tmr的计算方法一样，可以计算得到尾桨拉力Ttr，则尾桨产生的力与力矩在机体坐标系中的分量计算为：

(6)

(7)

Htr为尾桨桨毂与直升机重心垂直方向上的位置偏差；Dtr为尾桨桨毂与直升机重心水平方向上的位置偏差。

1.3 风阻和阻尼力矩

由于装备在小型直升机上的垂尾与平尾通常只有2～3 mm厚，剖面无拱形，所以产生的力小到可以忽略。因此，本文将机身、垂尾及平尾产生的力与力矩统一用风阻Fb,drag和阻尼力矩Mb,drag代替。

对于风阻Fb,drag，可以采用阻尼系数的方式表征为

(8)

u、v、w为机体坐标系下的飞行速度；Sref为参考面积，可以设置为机身某一方向投影面积；Cdx、Cdy、Cdz为机体坐标系3个方向上的阻力系数，阻力系数可以通过飞行数据辨识得到。

对于阻尼力矩Mb,drag，可以假设阻尼力矩和旋转角速度成反比，形式为

(9)

J=diag{Jxx,Jyy,Jzz}为直升机惯性矩矩阵(对于具有纵向对称面的小型无人直升机，其惯性矩矩阵主对角线以外的元素都很小，因此为简单起见可将其忽略)；Pp、Qq、Rr为阻尼力矩系数，一般通过实验数据辨识得到，为了形式简洁，统一通过转动惯量矩阵进行归一化处理。

1.4 完整的模型结构

综合上述分析，可以得到无人直升机在自转过程中受到的合力与合力矩为

(10)

Fb,g为重力矢量在机体坐标系中的投影。

(11)

直升机符合一般的刚体假设，由牛顿-欧拉方程可建立直升机的刚体运动方程组为

(12)

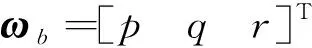
为了使模型结构参数化更强，可以对速度项去除运动学耦合和重力分量，转化关系为

(13)

则完整的直升机自转动力学模型为

(14)

Jmr为直升机主旋翼转动惯量。与直升机正常飞行时的动力学模型不同的是，直升机在失去动力后，直升机的转速将作为状态量用于直升机自转动力学建模。

此外，直升机姿态角和体轴系角速率之间的运动方程为

2）提高对身体健康的重视程度，加大对身体形态科学标准、维持良好体型重要意义的宣传。尤其针对偏胖或超重男生，减肥不是女生的专属，还必须成为男生的健康任务。在高校很有必要开设健身塑形的课程，成立健身俱乐部或健身社团，有条件的还可举办健身大赛。

(15)

2 控制策略

根据直升机自转过程中下降速度的变化情况，可将直升机自转过程分为加速下降、稳定下降和减速着陆3个阶段，如图1所示。

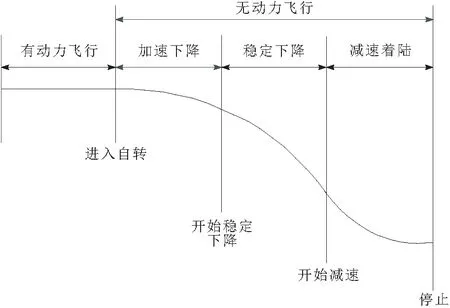
图1 直升机自转着陆飞行过程

2.1 加速下降阶段控制策略

加速下降阶段的任务是在动力失效后，以最快速度恢复或保持主旋翼转速，并快速进入稳定下降状态。

快速放开离合器：防止运行阻力导致主旋翼转速快速下降，因为亚拓760X传动系统的结构特性，动力失效后，主旋翼传动齿轮和电机齿轮自动离合，即主旋翼的转动将不会带动电机旋转。因此，在动力失效后，直升机主旋翼的反扭力矩将不会耦合至机身，有利于主旋翼动能的储存。

快速将总距降低：通过将主旋翼总距降低至负总距，使直升机进入加速下降阶段，在该阶段，直升机重力势能转化为主旋翼旋转动能，进而恢复并稳定转速。

2.2 稳定下降阶段控制策略

当直升机转速恢复或到达设定值后，进入稳定下降阶段，在该阶段，直升机接入主旋翼转速稳定控制律，转速控制最终通过总距操纵进行控制，控制策略如图2所示。

图2 稳定下降阶段控制策略

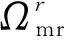
主旋翼转速稳定后，直升机以稳定的下降速度进行自转着陆，根据文献[10]，该稳定下降速度的经验值可估计为1.81vh，根据动量理论，即

(16)

2.3 减速着陆阶段控制策略

在减速着陆阶段，减速过早将导致主旋翼能量损失过大，同时仍远离地面，可能导致直升机硬着陆；相反的，若减速过晚，将导致直升机在着陆时无法达到期望的着陆速度，从而导致直升机硬着陆。

当直升机进入减速着陆阶段的临界高度hslow时，直升机进入减速着陆阶段，直升机开始执行减速着陆操作，hslow为

hslow=1+0.79w0

(17)

w0为稳定下降阶段的下降速度；hslow为实验得到的经验值。若直升机在临界高度hslow以上进行减速，则可能导致主旋翼动能损失过多，直升机失去控制权限，造成硬着陆；若直升机在临界高度hslow以下进行减速，则可能导致直升机没有足够的时间将下降速度控制到期望的速度，从而造成直升机硬着陆。

在该阶段，主要以下降速度控制为主，下降速度控制如图3所示。

图3 减速着陆阶段控制

2.4 总体控制结构设计

基于2.1～2.3节的控制策略及经典控制理论设计的小型无人直升机自转着陆飞行控制总体结构如图4所示。在进行自转着陆飞行控制时，首先要完成姿态内回路控制，保证直升机姿态的稳定性及可操纵性；其次根据自转着陆飞行需求设计直升机的速度、位置外环以及转速控制器，从而完成直升机自转着陆飞行控制。

图4 直升机自转着陆飞行控制系统结构

3 仿真实验

在MATLAB 2018b环境下，分别在直升机悬停状态初始高度为30 m和50 m初始状态下，进行了直升机自转着陆飞行仿真，图5～图8分别为在直升机归一化总距操纵量、主旋翼转速、下降速度及高度随时间的变化曲线。由图5～图7可知，直升机在不同高度下的自转着陆飞行均经历了3个阶段。

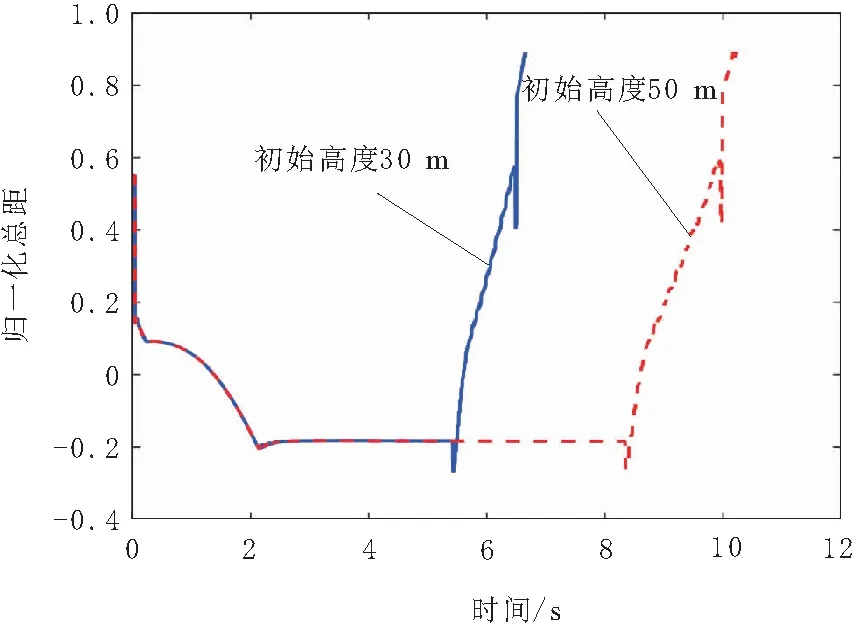
图5 直升机归一化总距变化曲线

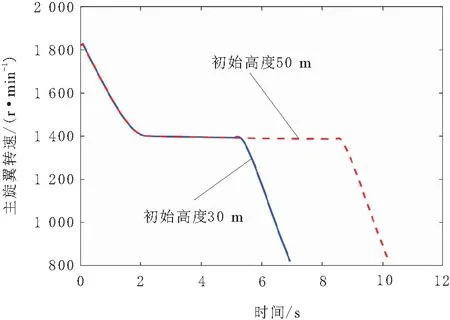
图6 直升机主旋翼转速变化曲线

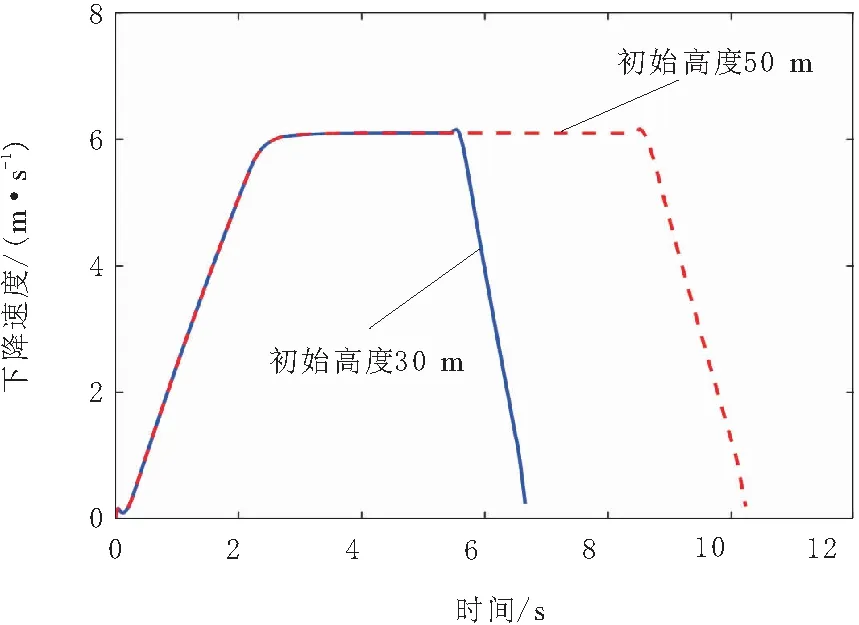
图7 直升机下降速度变化曲线

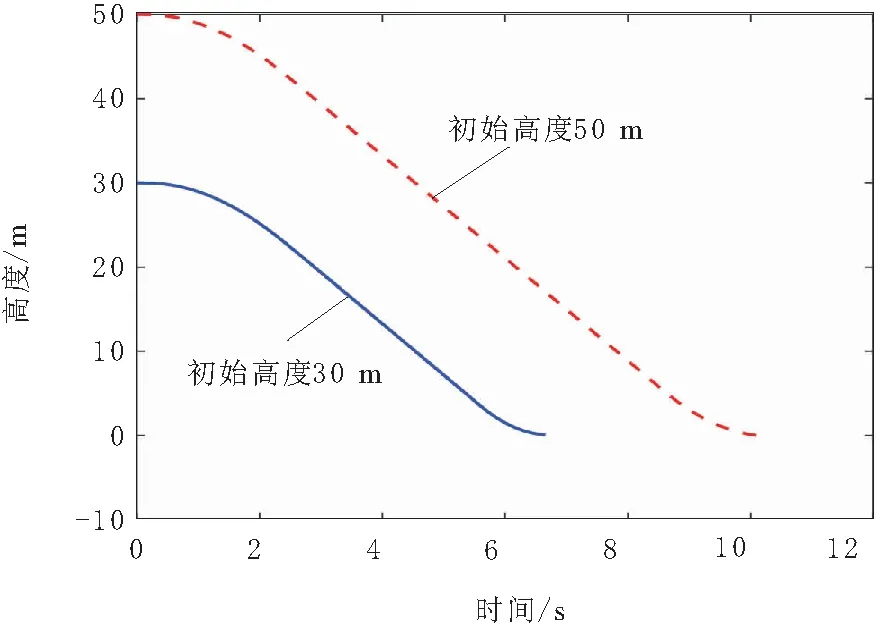
图8 直升机高度变化曲线

由图5可知，在加速下降阶段，总距不断减小，以防止直升机旋翼旋转动能下降过快；在稳定下降阶段，由于下降速度和旋翼转速基本稳定不变，所以总距也基本稳定不变；在减速着陆阶段，直升机开始减速着陆，因此总距不断增加，使旋翼拉力大于直升机重力，从而实现减速的目的。

由图6和图7可知，在加速下降阶段，由于直升机失去动力，旋翼转速不断减小，下降速度不断增大；在稳定下降阶段，直升机达到稳定状态，旋翼转速和下降速度基本稳定不变；在减速着陆阶段，由于总距不断增加，导致旋翼动能损失加剧，其转速不断减小，直升机开始减速着陆，最终触地着陆的速度约为0.2 m/s，触地速度较小。因此，直升机最终能够安全着陆，这说明了直升机自转着陆飞行控制策略的有效性。

由图8可知，直升机在50 m高度和30 m高度进行自转着陆飞行时，二者触地着陆的时间差约为3.6 s。由图5～图7可知，这主要是由于不同初始高度下稳定下降阶段的持续时间不同引起的。

直升机在自转着陆飞行过程中主旋翼转速变化趋势与文献[7]中所描述的基本一致，根据图7下降速度变化曲线可知稳定下降阶段的稳定下降速度约为6.11 m/s，而本文2.2节中采用文献[10]计算方法得到的稳定下降速度为5.98 m/s，说明所建立的模型具有较高的精度。

4 结束语

本文基于第一原理完成了小型无人直升机在自转着陆飞行状态下的主旋翼、尾桨以及风阻和阻尼力矩的动力学建模，通过对速度项去除运动学耦合和重力分量的影响，进而得到较为完整的直升机自转动力学模型，为小型无人直升机自转建模的研究提供了理论参考。针对直升机自转着陆飞行的3个阶段分别设计了以旋翼总距控制、旋翼转速控制和下降速度控制为主的PID控制策略。仿真结果表明，直升机在不同初始高度下完整的自转着陆飞行过程明显经过加速下降、稳定下降和减速着陆3个阶段，所设计的控制策略能够使直升机在触地时达到较小的下降速度，实现安全着陆。