直升机旋翼干扰对尾桨气动噪声影响的数值研究

2021-05-06邱逢昌曹亚雄

南京航空航天大学学报 2021年2期

樊枫，邱逢昌，曹亚雄

（中国直升机设计研究所直升机旋翼动力学重点实验室，景德镇333001）

直升机飞行时，尾桨常处于旋翼尾流场中，旋翼桨叶产生的螺旋桨尖涡会对尾桨有很强的干扰作用，旋翼/尾桨气动干扰一直是直升机型号研制中必须考虑的设计问题[1]。噪声特性是旋翼/尾桨干扰的重要方面，特别是旋翼尾流干扰下的尾桨噪声，是旋翼/尾桨干扰噪声特性的研究重点，这是因为前飞时，尾桨始终工作在旋翼的尾流中，旋翼桨尖涡与尾桨桨叶相接近甚至直接相碰，使得尾桨产生严重的桨-涡干扰噪声，从而导致尾桨噪声激增，甚至超过比尺寸较大的旋翼的噪声水平[2]。例如，Lynx 直升机在最初设计中，尾桨的旋转方向是“低向后”，飞行时尾桨产生了强烈的干扰脉冲噪声，而当改变尾桨旋转方向后，这个问题得到了解决[2]。因此，开展直升机旋翼/尾桨气动干扰噪声研究具有重要意义。

在旋翼干扰对尾桨噪声研究方面，国外已经开展了许多工作，并取得了一些进展。在早期，由于问题本身的复杂性和计算资源的限制，试验方法[3-4]是研究旋翼/尾桨干扰的主要方法，而理论计算起步较晚。2001 年，Yin 首先对旋翼/尾桨干扰噪声问题进行了数值计算，他采用非定常面元法和声学类比法对悬停状态和爬升状态的旋翼和尾桨的气动力和噪声进行了初步计算[5]。2008 年，英国利物浦大学Fletcher 等采用VTM 方法对旋翼、尾桨气动干扰和噪声展开了一系列的计算研究，得到了一些新结论[6-7]。2004 年，日本学者Yang 首次采用CFD 方法针对旋翼干扰下的尾桨噪声进行了初步计算[8]。2011 年，Yin 进行了BO-105 直升机旋翼/尾桨干扰的研究[9]，并与“HeliNOVI 项目”[10]的试验结果进行了对比。他们的结果表明：对于BO-105 直升机，尾桨噪声在直升机爬升、大速度平飞状态具有重要影响，且对尾桨旋转方向较为敏感。2019 年，Mehmet 等采用CHARM 综合分析软件（尾迹方法）和声学类比法围绕尾桨构型参数对旋翼/尾桨干扰噪声特性开展了初步的计算研究[11]；而Arda 等则采用黏性涡粒子方法计算研究了旋翼气动干扰对尾桨气动力的影响[12]。

数值模拟旋翼干扰下的尾桨干扰噪声特性的关键在于能够准确地模拟旋翼尾迹与尾桨桨叶的干扰流场。而CFD 方法在求解旋翼尾桨干扰流场时，能够准确描述桨叶表面的非线性流动以及尾迹的复杂运动特征，这对于模拟旋翼/尾桨干扰的复杂流动，尤其是涡-面碰撞等，具有明显优势。至目前，国外采用CFD 方法计算尾桨气动干扰噪声特性的研究很少，国内鲜有相关公开发表文献。本文采用CFD/FW-H 方法针对旋翼干扰下的尾桨干扰噪声特性开展计算研究，着重开展不同飞行状态下，尾桨旋转方向、垂向位置对旋翼/尾桨干扰噪声影响的研究。

1 计算模型及验证

1.1 旋翼/尾桨气动干扰分析模型

旋翼/尾桨非定常载荷采用文献[13]中的旋翼/尾桨气动干扰CFD 方法进行计算。该方法通过对空间进行有限体积的离散进行求解，控制方程采用非定常雷诺平均RANS 方程，即

式中：W 为守恒变量，F(W )，G(W )分别为无黏通量和黏性通量。空间离散为Roe-MUSCL 格式，非定常时间的推进采用双时间法，伪时间上采用隐式LU-SGS 格式，湍流模型为S-A 一方程模型。针对旋翼、尾桨的运动，采用在Inverse-Map 基础上发展而来的扰动衍射法[14]，其具有网格自动加密策略，更适于旋翼、尾桨干扰下的运动嵌套。

由于缺乏旋翼/尾桨干扰气动特性的试验数据验证，文中采用Helishape 7A 旋翼[15]和Robin 旋翼/机身干扰模型[16]进行计算，以验证方法的有效性。图1 给出了不同r/R 比下，7A 旋翼桨叶截面法向力系数试验值与计算值对比曲线。图2 给出了前进比μ=0.23 时，不同观测点（14、15）的Robin 机身顶端非定常压力系数计算值与试验值的对比。由图可见，计算与试验值吻合较好。这表明计算模型适合于预估桨叶非定常气动载荷，也能够有效地分析直升机干扰流场。

图1 Helishape 7A 旋翼桨叶剖面法向力系数试验值与计算值对比Fig.1 Comparison between experimental and calculated val-ues of sectional normal force coefficient of Helishape 7A rotor

图2 Robin 机身顶端非定常压力系数计算值与试验值的对比（前进比μ=0.23）Fig.2 Comparison of calculated and experimental unsteady pressure coefficient on top of Robin fuselage（For-ward ratio μ=0.23）

1.2 基于FW-H 方程的噪声计算模型

本文噪声预测采用的是混合方法，即由1.1 节中建立的方法获得尾桨表面非定常气动力分布，再通过声学类比法（FW-H 方程）将非定常气动力、运动、几何外形等引起的声场扰动传播至远场。这里直接给出FW-H 方程的积分求解公式Farassat 1A（F 1A）公式[17]，即

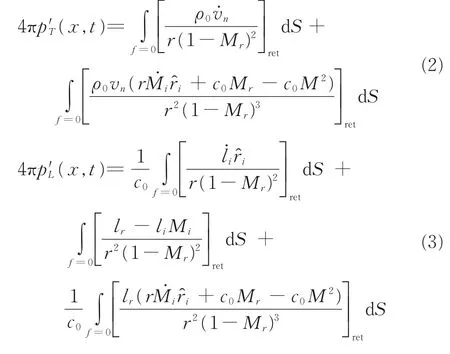
式（2～3）中参数解释请参考文献[17]。

图3 给出了不同桨尖马赫数（MaTIP）及观测点位置（3.09R 及2.18R）下，UH-1H 直升机旋翼[18]悬停状态厚度噪声声压历程计算对比曲线。图4 给出了10014 状态下，不同观测点（#3、#7）的AH-1/OLS 旋翼[18]典型桨-涡干扰状态噪声声压计算与试验值的对比。由图可见，本文计算模型较为准确地分辨出了厚度噪声和桨-涡干扰噪声声压幅值和相位，这表明了本文方法的有效性和准确性。

图3 UH-1H 旋翼噪声声压历程计算对比Fig.3 Comparison of noise pressure of UH-1H rotor

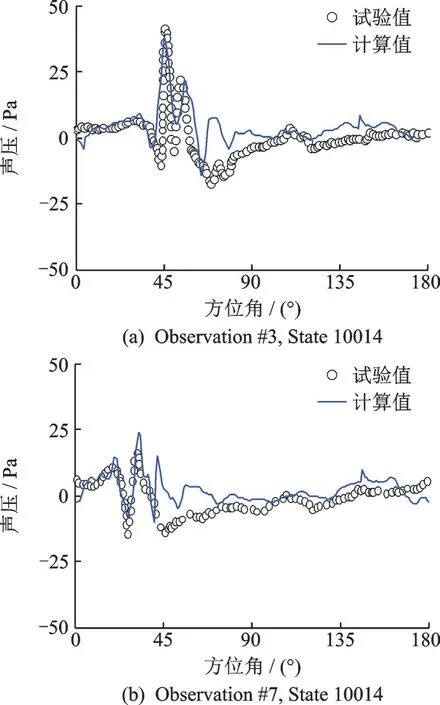
图4 典型桨涡干扰状态AH-1/OLS 旋翼声压历程计算值与试验值对比Fig.4 Comparison of calculated and experimental results of noise pressure of AH-1/OLS rotor during blade-vor-tex interaction

2 计算与分析

2.1 旋翼/尾桨干扰计算模型

本文用于旋翼/尾桨干扰计算的桨叶模型参数如表1 所示，其中旋翼、尾桨桨尖速度相同，尾桨半径Rt取为旋翼半径R 的1/5。

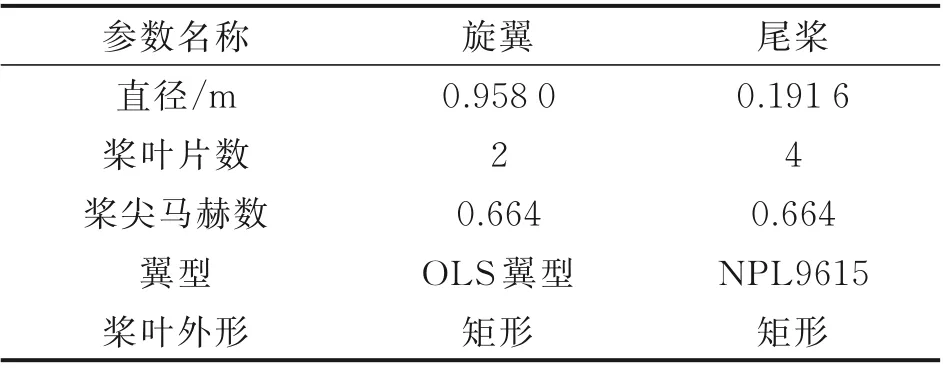
表1 旋翼和尾桨参数表Table 1 Parameters of rotor and tail-rotor

图5 给出了本文计算中尾桨相对位置示意图。旋翼和尾桨的纵向间距为1.25R（旋翼半径），侧向间距为0.085R。尾桨旋转方向包括“底向前”和“底向后”。前者是指尾桨转至底部时转动方向向前，后者相反；尾桨垂向位置有“高位”尾桨，即尾桨与旋翼等高度和“低位”尾桨，尾桨位于旋翼桨盘平面下方0.12R（0.6Rt）处。本文高、低位尾桨垂向位置是参考文献[19]进行选择的，“高位”尾桨大致对应于UH-60 尾桨位置，“低位”则对应着AH-64 尾桨位置。文中分析尾桨垂向位置影响时，尾桨旋转方向同为“底向前”；分析尾桨旋转方向影响时，尾桨垂向位置固定在“高位”。

图5 旋翼/尾桨相对位置示意图Fig.5 Schematic of relative positions of main-rotor and tail-rotor

图6 给出了计算网格系统示意图。旋翼和尾桨的桨叶网格均采用C-H 型结构网格，前者的网格尺度为201×38×86（弦向×法向×展向），后者为207×42×76；背景网格则采用笛卡尔网格（300×147×253）。全部网格数量约为1 500 万。尾桨的转速是旋翼转速的5 倍，在物理时间步一致的条件下，考虑程序收敛性等问题，旋翼及尾桨步进角度分别设为1.0°及0.2°。

图6 旋翼/尾桨干扰计算网格系统示意图Fig.6 Grid system for main-rotor and tail-rotor interference calculation

本文选取了直升机3 个典型的飞行状态进行研究，即悬停状态、低速前飞状态以及巡航状态，具体飞行参数如表2 所示。表中Matip为桨尖马赫数，μ 为前进比，θ0为尾桨桨叶总距，θ1c为横向周期变距，θ1s为纵向周期变距。其中，前进比μ 结合国外已有的旋翼操纵量和运动规律的试验值确定，尾桨桨叶总距保持为8°。

表2 旋翼运动和操纵参数Table 2 Control parameters of rotor

2.2 悬停状态

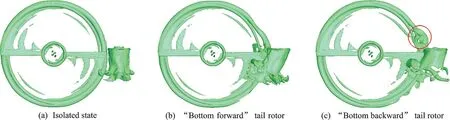
图7 悬停状态旋翼/尾桨干扰流场等涡量图Fig.7 Vorticity contours of rotor/tail rotor interaction in hovering state

图7 给出了不同尾桨转动形式下干扰流场的等涡量图。由图可见，悬停状态下受旋翼流场影响，尾桨涡向旋翼侧产生了一定程度的倾斜，“底向前”状态要大于“底向后”状态。从图中也可以看出，“底向后”尾桨的涡流场混乱程度要明显大于“底向前”尾桨。

图8 给出了尾桨拉力随方位角的变化曲线，在旋翼干扰下尾桨拉力出现了明显的振荡，这种振荡与尾桨涡流场的混乱程度有直接关系。从图8(a)中可明显看出，“底向前”尾桨拉力的振荡要小于“底向后”构型。图8(b)中“低位”尾桨的拉力振荡程度要明显强于“高位”尾桨，且其平均拉力也大于“高位”尾桨和孤立尾桨。这是由于“低位”尾桨所处的轴向位置较“高位”尾桨低些，该处的旋翼诱导流场因流管收缩而加速，从而使得旋翼对尾桨的干扰影响增大。

图8 悬停状态时尾桨拉力系数随方位角的变化曲线Fig.8 Variation of tail rotor thrust coefficient with azimuth in hovering

为分析尾桨噪声辐射特性，选择了距尾桨旋转中心30 m 且垂直于尾桨桨盘的平面作为观测点，其尺寸为150 m×100 m，尾桨位于计算平面的中心处。图9 给出了悬停状态时观察平面处孤立尾桨厚度噪声声压级(Sound pressure level, SPL)的分布图。厚度噪声在桨盘平面最大，而在桨盘外侧噪声逐渐地减小。由于厚度噪声只与桨叶的几何特征和运动状态相关，而不受桨叶载荷影响，所以干扰状态下的厚度噪声与孤立尾桨相同，这里不再重复给出。

图9 悬停状态时孤立尾桨厚度噪声SPL 分布图Fig.9 Distribution of tail-rotor thickness noise SPL in hovering

图10 给出了尾桨载荷噪声SPL 分布图。与孤立尾桨相比，各构型组合下的尾桨载荷噪声声压级的最大值和平均值要比孤立尾桨大，这显然是旋翼对尾桨的气动干扰所引起的。对比“底向前”和“底向后”尾桨载荷噪声在尾桨轴线方向的分布规律可以看出，“底向后”尾桨的载荷噪声要比“底向前”尾桨平均大1 dB 左右。另外，比较图10(b)和图10(d)可以发现，虽然“低位”尾桨载荷噪声声压级的最大值与“高位”尾桨相近，但前者载荷噪声的平均水平要比后者大1 dB 多。

图11 给出了各构型下尾桨总噪声SPL 分布图。在该状态下厚度噪声占主导，因而总噪声的变化趋势与图9 厚度噪声分布类似。综合前面结果，可以看出悬停状态时旋翼对尾桨的气动干扰影响会导致尾桨噪声水平增大，尤其是载荷噪声水平增大。总体而言“底向前”尾桨的噪声特性要优于“底向后”尾桨，而“高位”尾桨要优于“低位”尾桨。

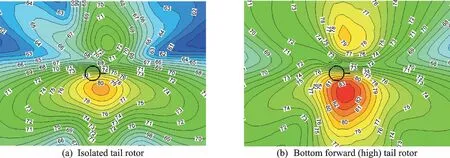
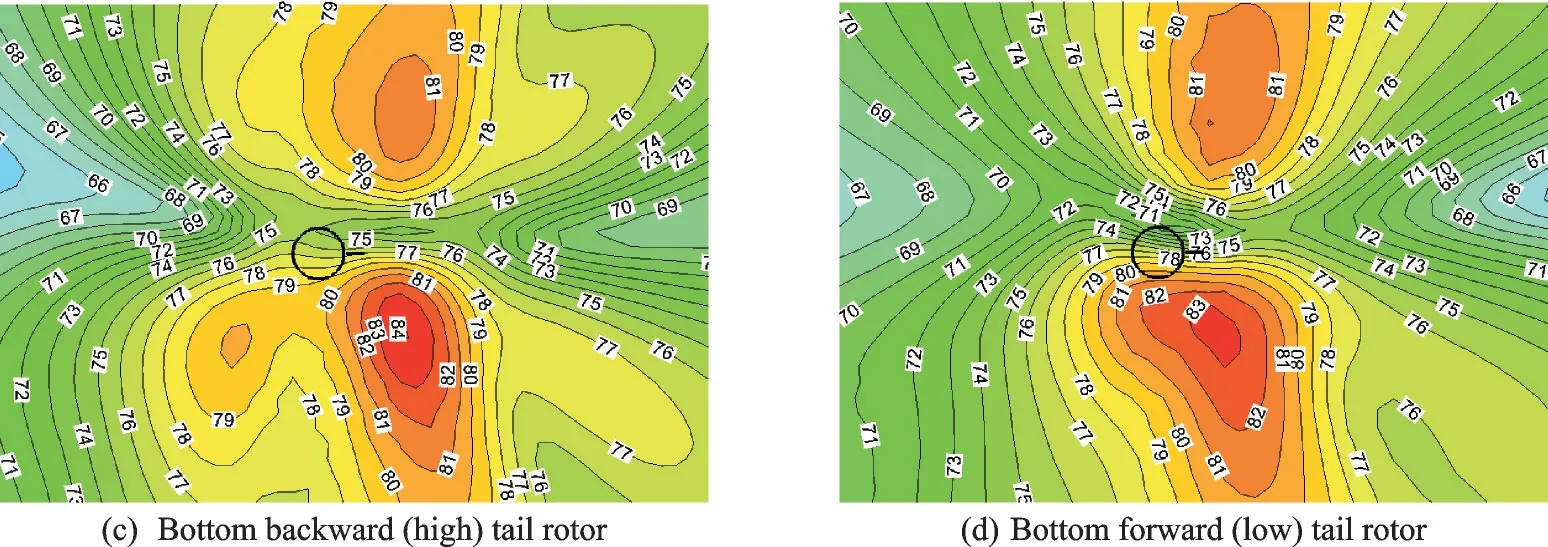
图10 悬停状态时尾桨载荷噪声声压级分布图Fig.10 Load noise SPL of tail-rotor in hovering

图11 悬停状态时尾桨总噪声分布图Fig.11 Total noise SPL of tail-rotor in hovering

2.3 低速前飞状态

图12 为前飞状态下旋翼、尾桨干扰的等涡量流场图。旋翼桨叶的桨尖涡会穿过尾桨平面。当旋翼尾迹通过尾桨平面时，旋翼尾迹形状会发生一定的畸变，而这种畸变正是传统尾迹方法较难处理的，这也体现了CFD 方法的优越性。

图13 给出了尾桨拉力系数时间变化曲线。图13(a)中可见，“底向前”尾桨的拉力振荡幅值要明显大于常规尾桨，而“底向后”尾桨则能有效地降低这种拉力振荡，这对直升机的操稳特性是有利的。图13(b)中“高位”尾桨的拉力变化要比孤立尾桨剧烈得多，而“低位”尾桨则略显缓和。这是因为“高位”尾桨桨叶与旋翼尾迹相遇的截面要比“低位”尾桨更靠外些，而桨叶外段对尾桨的气动特性影响更大。

图12 前飞状态旋翼/尾桨干扰流场涡量图Fig.12 Vorticity contours of rotor/tail rotor interaction in forward flight

图13 低速前飞状态时尾桨拉力系数随方位角的变化曲线Fig.13 Variation of tail rotor thrust coefficient with azimuth in low-speed flight

图14 给出了尾桨厚度噪声SPL 分布，观察平面与悬停状态时相同。前飞状态时厚度噪声向前传播，且由于厚度噪声不受干扰影响，使得其仍保持着基本对称的特征。对比“底向前”尾桨和“底向后”尾桨的厚度噪声，前者噪声整体水平要低于后者，这是因为尾桨桨叶前行侧的运动速度要大于后行侧，而“底向前”尾桨更接近观察平面。

图15 计算了低速前飞时旋翼干扰下的尾桨载荷噪声SPL 在观察平面上的分布情况。由图可见，各组合构型下的尾桨载荷噪声均要比孤立状态大。对比“底向后”和“底向前”尾桨可以发现，“底向后”尾桨在观察平面上的载荷噪声要明显大于“底向前”尾桨，前者的平均载荷噪声声压级要比后者大2～3 dB。对比图15(b)和图15(d)可以看出，“高位”尾桨的载荷噪声水平也要大于“低位”尾桨，这与尾桨垂向位置对法向力的影响规律是相符的。

图14 低速前飞时尾桨厚度噪声分布图Fig.14 Thickness noise SPL of tail-rotor in low-speed flight

图16 出了该状态下尾桨总噪声SPL 在观察平面处的分布情况。可以看出，该状态下各构型组合的尾桨载荷噪声的整体水平均要大于孤立尾桨。“底向前”尾桨在桨盘前方的载荷噪声要大于“底向后”尾桨，而在桨盘后方后者则小于前者，这仍是因为尾桨在前行侧和后行侧的载荷噪声不同的缘故。比较图16(b)和图16(d)能够发现，“高位”尾桨的总噪声水平要略大于“低位”尾桨，这与载荷噪声的情况一致。

2.4 巡航状态

图17 给出了巡航飞行时“底向前”尾桨和“底向后”尾桨的厚度噪声SPL 特性，从图中可以看出，与低速前飞状态相同，“底向前”尾桨的厚度噪声水平要大于“底向后”尾桨，这仍是尾桨桨叶在前行侧的运动速度大于后行侧的缘故。

图15 低速前飞时尾桨载荷噪声分布图Fig.15 Load noise SPL of tail-rotor in low-speed flight

图16 低速前飞时尾桨总噪声分布图Fig.16 Total noise SPL of tail-rotor in low-speed flight

图17 中速前飞时尾桨厚度噪声分布图Fig.17 Thickness noise SPL of tail-rotor in cruise-speed flight

图18 给出了巡航状态时尾桨载荷噪声SPL分布。在尾桨旋转方向为底向前时，旋翼干扰下尾桨载荷噪声的最大值要略低于孤立尾桨，但在其他地方，旋翼干扰下的载荷噪声仍要大于孤立尾桨；“底向后”尾桨的载荷噪声水平要比“底向前”尾桨大许多，这与低速前飞时的情况是相似的。图19 为尾桨总噪声SPL 的分布。总体而言，“底向前”尾桨的总噪声水平小于“底向后”尾桨，而“高位”尾桨的总噪声水平则小于“低位”尾桨。