装配面点云特征增强的去噪算法研究

范 晨，金 永，刘静静，孙煜雅

(中北大学信息与通信工程学院，山西 太原 030051)

0 引言

法兰装配面点云数据是通过激光扫描设备获取的，但是由于扫描设备的精度、实验环境的光照以及激光入射角度等因素的干扰产生了不同类型的噪声。这些噪声点的存在往往会严重影响重建后的表面精度。装配面上又含有台阶面等特征，则对噪声去除的同时需要保持并增强特征点云，这对精确测量装配面的尺寸信息具有重要意义。因此，法兰装配面点云数据的去噪处理是必要的。目的是去除噪声、获得装配面曲面更高平滑度的同时，尽可能保持它的几何特征，防止产生过度光顺的现象。

目前，国内外学者对点云去噪提出了多种不同的算法。其中，Fleishman[1]和Jones[2]最早在论文中提出了网格的双边滤波去噪法；Wang等[3]最先在三维空间中运用了移动最小二乘法(moving lest squares,MLS)去噪法；刘静静[4]提出的改进双边滤波法；Lu等[5]改进了网格去噪法；郭东兵[6]将传统的三步网格去噪法改进为了四步；袁华等[7]提出一种基于噪声分类的双边滤波点云去噪算法。虽然网格法和双边滤波法都可以实现滤波去噪的效果，但是网格法处理结果易出现形状畸形或表面收缩的现象，且在对数据网格化时有可能会将误差引入，因此，本文选择使用了双边滤波法对装配面点云数据进行处理。

本文以法兰装配面作为研究对象，针对法兰装配面上含有的特有噪声点和特征点，将噪声点进行了分类，利用空间栅格划分将点云数据栅格化，使用K领域搜索的方法筛选出第1类噪声点，运用采样点邻域点数统计法删除第1类噪声点；采用提出的改进双边滤波法对第2类噪声点进行去噪。最后通过与各类算法进行对比分析，检验算法在法兰装配面点云数据上的去噪效果以及特征的保持度。

1 装配面点云数据的去噪

三维点云数据一般分为有序点云数据和散乱点云数据[8-12]。对于有序点云数据的去噪来说，常用的算法包括中值滤波算法、高斯滤波算法、随机滤波法和最小二乘滤波等。对于散乱点云数据的去噪来说，也有2种常用的方法，分别是：

a.直接对含噪声的散乱点云进行滤波去噪处理。

b.将含噪声的散乱点云数据网格化后进行滤波去噪处理。点云数据去噪是为了有效且快速地去除噪声点，与此同时保持点云的细节特征。

装配面点云数据的噪声组成分为2类，第1类是由于光照环境或材料本身的异常反射，数据中产生一些游离于主体曲面之外呈独立分布的噪声点，称外点；第2类是与主体曲面点云混合的呈散乱、随机分布的噪声点，称离散点[13]。如图1和图2所示。

图1 原始法兰装配面点云数据

图2 点云数据孔洞处噪声放大

本文对装配面点云数据去噪的整体步骤为：

a.对装配面点云数据中的噪声点进行分类。

b.根据空间栅格划分的方法将点云数据栅格化。

c.使用K领域搜索的方法，确定法兰装配面点云的空间位置，判断每片点云的栅格数量是否最多。

d.如果不是最多那就是第1类噪声点，利用采样点邻域点数统计的方法删除第1类噪声点。

f.接下来就是比较Ti与阈值T0的大小。当判断Ti>T0为是时，就认定为特征点云，利用K邻域来计算α(双边滤波因子)；当判断Ti>T0为否时，就认定为非特征点，利用栅格内的点云来进行计算。

g.利用改进的双边滤边法对第2类噪声点进行去噪。

具体的去噪流程如图3所示。

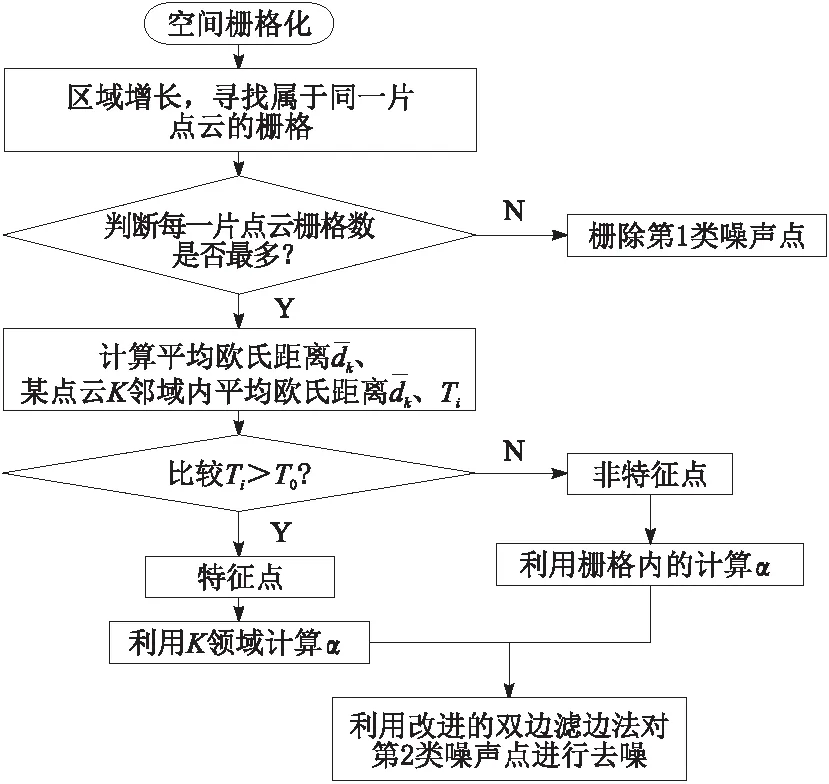
图3 装配面点云去噪流程

1.1 法兰装配面点云栅格化

确定法兰装配面的空间位置时使用了空间栅格划分的方法，将法兰装配面点云数据按x，y，z划分成A，B，C这3个部分。装配面点云空间栅格化的目的在于求出每个点所在的栅格位置以及确定每个栅格中点云的个数。具体步骤为：

a.读入点云数据。

b.将法兰装配面点云的坐标点存入一维数组中，得到其x，y，z坐标的最大值、最小值。

c.在包围所有的数据点的长方体包围盒中，根据法兰装配面点云数据点的密度将长方体包围盒划分成一个个小立方体栅格。

设xmax、xmin为包围盒x轴上的最大、最小坐标；ymax、ymin为包围盒y轴上的最大、最小坐标；zmax、zmin为包围盒z轴上的最大、最小坐标；L为包围盒中栅格的长度。那么，3个不同方向上小立方体栅格的个数分别为：

(1)

(2)

(3)

设Qx、Qy、Qz分别为某个点的三维坐标值，那么就有：

(4)

(5)

(6)

E、F、G分别为某点所在3个方向上立方体栅格的索引号。文中使用了存储数组来记录每个栅格中全部数据点的序号，A×B×C为数组中元素的个数。

1.2 第1类噪声去除

法兰装配面点云数据中的第1类噪声点(外点)，与传统的噪声干扰有明显的不同，它具有明显独立分布的特性，并且游离于主体曲面点云之外。第1类噪声点(外点)会严重影响法向量、点云密度以及曲率的求取。因此，对于第1类噪声点的去除也是必要的。

具体步骤为：

a.首先将法兰装配面点云数据设为Q={Qi,i=1,2,…,N,Qi∈R3}。

b.对点云中每个Qi提取其K邻域NB(Qi,K)={Qi1,Qi2,Qi3,…,QiK}。

(7)

(8)

(9)

图4 未去除第1类噪声点

图5 去除第1类噪声点

1.3 第2类噪声去除

法兰装配面点云数据在去除第1类噪声点后，还会存在一些离散的噪声点，称其为第2类噪声点(离散点)这类噪声与真实主体曲面点云混合在一块。第2类噪声点会严重干扰曲面重建的光顺度，并且还会使点云表面发生起伏进而产生失真现象。因此，对第2类噪声点的去除也是必要的。

提出了一种改进的双边滤波点云去噪算法。将Q′=Q-αn定义为改进的双边滤波算法。其中，Q为原始点；Q′为去噪点；n为法矢方向；α为双边滤波因子，即

α=

(10)

2 实验结果与分析

为了验证算法的去噪效果，本文算法与多种点云去噪算法进行了对比分析。去噪效果如图6～图10所示，图中数值单位为mm，各算法在处理装配面点云数据时，本文算法的去噪效果是最好的。

图6 文献[6]去噪效果

图7 文献[7]去噪效果

图8 文献[8]去噪效果

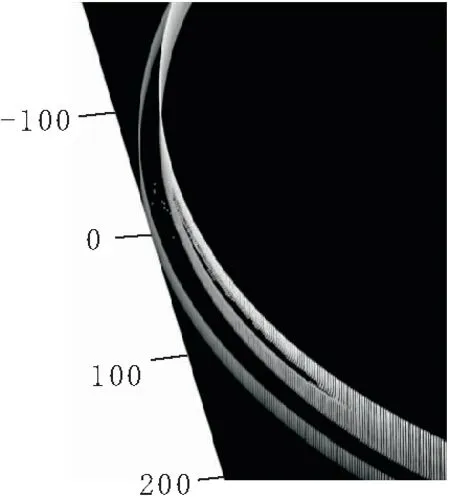
图9 文献[9]去噪效果

图10 本文算法去噪效果

用MSAE值[14]进行对比分析， 它是原点云的法向量与去噪后点云法向量差异的最小绝对误差和，用来衡量去噪结果的保真程度。由表1可知，本文算法对数据的保真度要高于其他算法。

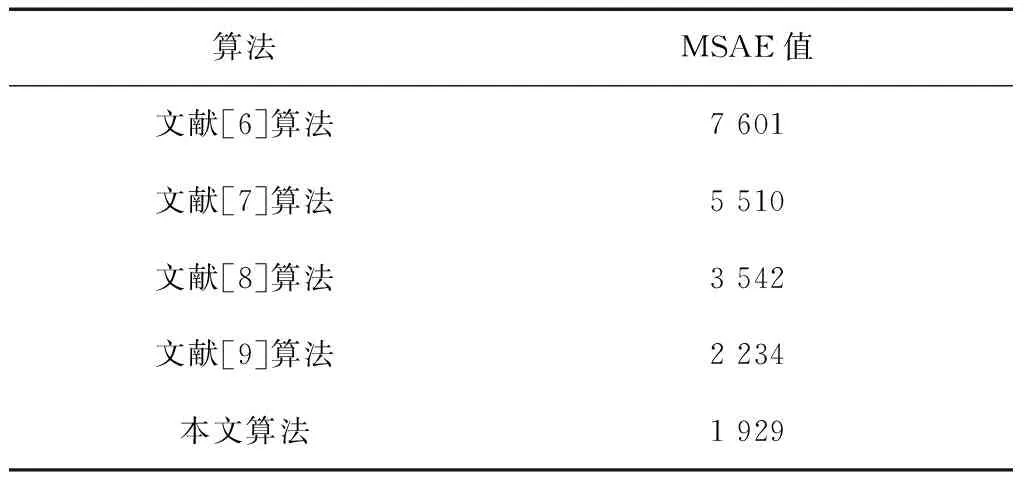
表1 MSAE值对比表

本文的法兰装配面点云数是932 260。表2是各算法处理法兰装配面点云数据噪声时的耗时，从表2可以看出，处理相同的装配面点云数据，本文算法所消耗的时间更短。

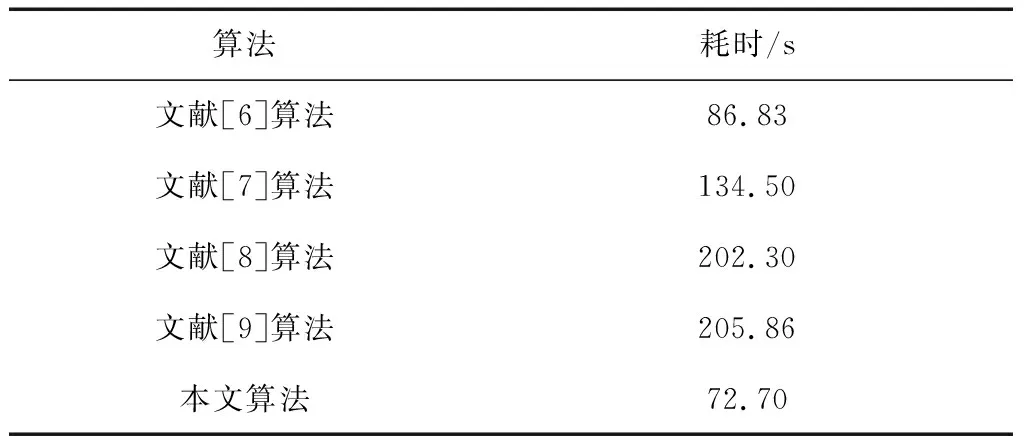
表2 耗时对比

由实验结果对比可见，不论是从算法耗时、算法的处理效果，还是点云数据的保真效果方面，本文算法取得了较好的去噪效果，同时也保持了点云数据的细节特征。

3 结束语

本文提出了一种改进的双边滤波去噪算法，主要针对了第2类噪声点的去除，通过邻域点判断是否属于特征点，再使用改进的算法对其进行去噪。通过与各类算法进行对比分析，本文的去噪算法在达到预期去噪效果的同时还可以增加装配面特征的保持度，且避免了传统双边滤波在去噪后产生光顺过度的现象。

本文算法也存在一定的局限性：

a.本文算法中的阈值，来源于多次试验结果的设定，下一步工作应研究阈值的自适应选取。

b.当遇到海量的点云数据时，本文算法的计算耗时会更长，下一步要对算法的计算效率进行优化。