基于最优IMF分量和K-SVD的滚动轴承故障声音信号特征提取

梁雄鹤，陈 珊，魏 豪，张丽洁，权 伟

(西安工程大学机电工程学院，陕西 西安 710048)

0 引言

滚动轴承作为机械设备的关键部件[1]，已经在各个领域得到了广泛的应用，其故障发现若不及时，会造成设备停机甚至损坏，因此，监视诊断滚动轴承状态尤为重要。振动传感器成本昂贵，而声音传感器性价比高，且发展前景良好，但相比振动传感器，声音传感器受环境噪声严重，导致所采集的故障信息更微弱[2]。滚动轴承一旦出现点蚀、裂纹或剥落，其声音信号中会产生周期性冲击成分，但通常被噪声所淹没，导致很难有效地诊断故障[3]。

针对上述问题，国内外学者提出了许多解决方法，如经验模态分解(EMD)[4]、最大熵解卷积(MCKD)[5]、字典学习[6]和变分模态分解(VMD)[7]。Zheng等[8]提出了一种基于NLM-KSVD的方法，该方法能准确提取滚动轴承故障特征频率；Liang等[9]提出了一种基于IK-SVD的方法，该方法具有良好的滚动轴承故障检测性能;余发军等[10]提出了一种基于字典学习的方法，能更好匹配早期故障特征成分；张文颢等[11]提出了一种基于K-奇异值分解(K-SVD)字典和HBW-OOMP算法的故障轴承诊断方法，能有效提取强背景噪声下故障特征成分。然而，在强背景噪声下，轴承故障信号SNR低导致传统K-SVD字典学习方法提取故障特征更加困难。VMD是一种新的信号分解方法，其通过将信号分解成一系列IMF分量， Li等[12]提出了一种基于VMD-FRFT的方法，成功实现了对滚动轴承的诊断；王恒迪等[13]提出了一种基于参数优化的变分模态分解的方法，更有效地提取轴承早期故障特征。国内外学者主要利用峭度指标来选取最优IMF分量，然而峭度受噪声影响大，容易造成最优IMF分量误选。相比峭度指标，SAF指标[14]具有良好的抗噪性和稳定性。

因此，本文提出了一种基于最优IMF分量与K-SVD结合的方法。仿真及实验结果表明，相比传统K-SVD字典学习方法，本文方法能更准确地提取滚动轴承声音信号中周期性冲击成分，从而有效地实现对轴承故障的诊断。

1 基本理论

1.1 K-SVD算法

K-SVD算法是一个稀疏编码和字典更新交替进行的过程，其核心思想是逐列更新字典的原子。目标优化函数为

(1)

Y为原始信号所构成的样本矩阵；D为学习字典矩阵；X为稀疏系数矩阵；xj为X的第j行；T0为稀疏度。固定字典D，通过OMP算法更新稀疏系数xj，最后逐列更新字典。计算更新原子的误差矩阵Ek，即

(2)

dj为字典D的第j列；xj为稀疏矩阵X的第j行；dk为字典D的第k列；xk是稀疏矩阵X的第k行。确定出稀疏稀疏矩阵X中所有非零项xj的位置集合Ω，并根据Ω选出Ek中所对应位置的列E，对E进行奇异值分解，即

E=UΔVT

(3)

通过矩阵U的第1列更新字典矩阵中的原子；矩阵V的第1列与Δ(1,1)相乘的值作为稀疏系数xj，依次完成稀疏表示字典的更新。

1.2 VMD算法

VMD是一种新的自适应非平稳信号处理方法，是一种基于希尔伯特变换、维纳滤波、频率调制的多分量信号分解算法。通过寻找约束变分模型最优解确定每个分量的频率中心及带宽，实现对信号不同频率分量的自适应分离。根据VMD的基本原理，通过以下步骤获取模态函数uk(t)的带宽。

a.对模态函数uk(t)进行希尔伯特变换，即

(4)

b.式(4)加入指数函数用来调整各分量预估的中心频率，将对应的频谱调制到相应的基频带，即

(5)

c.获得每个IMF分量的中心频率wk；通过计算解调信号梯度L的平方估算出各分量的带宽，对应的约束变分模型为

(6)

{uk}={u1,…,uk}为K个IMF分量；{wk}={w1,…,wk}为各个IMF分量的中心频率。

1.3 SAF指标

SAF定义为IMF分量的傅里叶变换幅度谱与原始信号x(t)在同一频率区间内的幅度谱之比。根据SAF指标选择的最优IMF分量不随噪声强度变化，与峭度指标相比，具有良好的抗噪性和稳定性，其数学表达式为

(7)

Po(n)为原始信号的傅里叶变换幅度谱；Pk(n)为第k个IMF分量的傅里叶变换振幅谱；fi为理论故障特征频率；2δ为以fi为中心的频宽，以保证实际故障频率在以理论故障频率fi为中心的频带内。

2 本文算法

针对传统K-SVD方法在构建字典原子时受噪声干扰严重，导致得到的稀疏信号无法准确识别轴承故障特征频率的问题，提出了一种基于最优IMF分量结合K-SVD的方法，算法流程如图1所示。

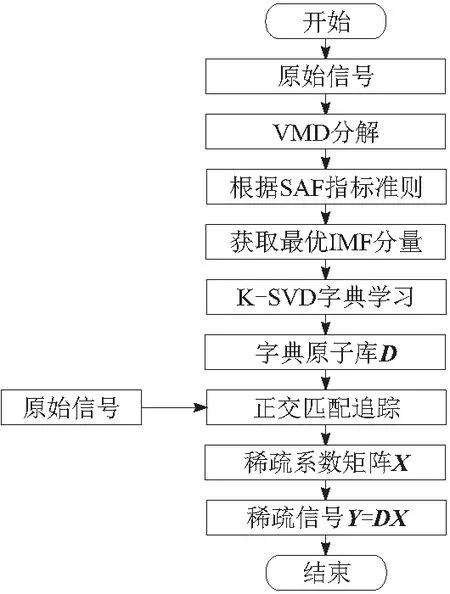
图1 最优IMF分量和K-SVD方法流程

具体步骤如下所述：

a.利用VMD分解原始信号，得到K个IMF分量。

b.计算每个IMF分量的SAF指标值，根据SAF指标最大化准则选取最优IMF分量。

c.将步骤b选取的最优IMF分量作为K-SVD字典学习的训练信号，获取能准确匹配轴承故障冲击的字典原子库。

d.将原始信号和步骤c所得字典原子库作为OMP的输入，从而获得稀疏信号。

e.对步骤d所得稀疏信号进行包络谱分析，提取故障特征频率，从而达到对轴承周期性冲击故障的准确识别。

3 仿真验证

本节通过对轴承外圈故障的仿真信号进行分析，并与传统K-SVD字典学习方法对比，以验证本文方法的有效性。仿真信号为

(8)

A=0.4 m/s2为幅值系数；ε=0.08为系统阻尼系数；fd=2 500 Hz为系统共振频率；n(t)为加入的高斯白噪声；外圈故障周期T=0.02 s，故障频率f=50 Hz；采样频率fs=10 kHz；采样时间为0.5 s。

仿真信号如图2所示，图2a、图2b分别为故障冲击信号时域图、加噪后的信号时域图，可知周期性冲击信号被噪声淹没；图2c为仿真信号的包络谱图，发现从仿真信号包谱图中几乎观察不到50 Hz的故障特征频率，完全被其他干扰频率所淹没，导致根本无法准确识别到周期性冲击故障特征频率。

图2 仿真信号

利用VMD对上述仿真信号进行分解，得到5个IMF分量。计算各IMF分量的SAF指标值，如表1所示，根据SAF指标值最大化准则可知IMF4数值最大，为最优IMF分量，作为训练信号。

表1 IMF分量和SAF指标值

将本文方法与传统K-SVD字典学习方法进行对比，结果如图3所示。图3a、图3b为传统K-SVD字典学习方法所得稀疏信号的时域图和包络谱图；图3c、图3d为通过本文方法获得的稀疏信号时域图和包络谱图。对比图3a、图3c可发现，本文方法所得稀疏信号时域图含噪信息更少，可观察到周期性冲击信息，而传统K-SVD字典学习方法获得的稀疏信号时域图几乎看不出任何周期性冲击信息；对比图3b、图3d，可知本文方法能更清楚地提取故障冲击频率50 Hz以及倍频信息且幅值较高，而传统K-SVD字典学习方法只能看到微弱的故障冲击特征频率且幅值较低。仿真结果表明本文所提方法的有效性和优越性。

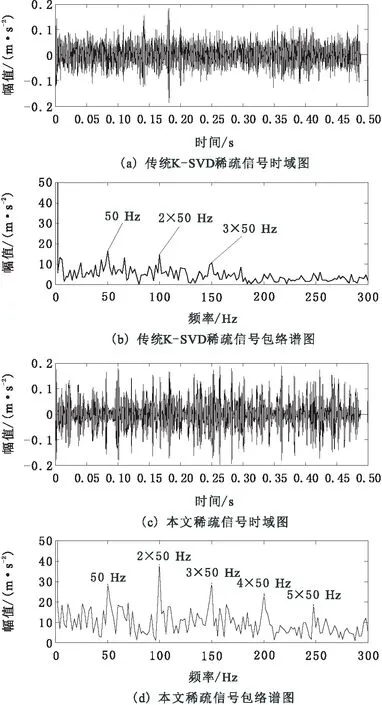
图3 仿真信号稀疏后的信号

各信号和SNR指标值如表2所示。

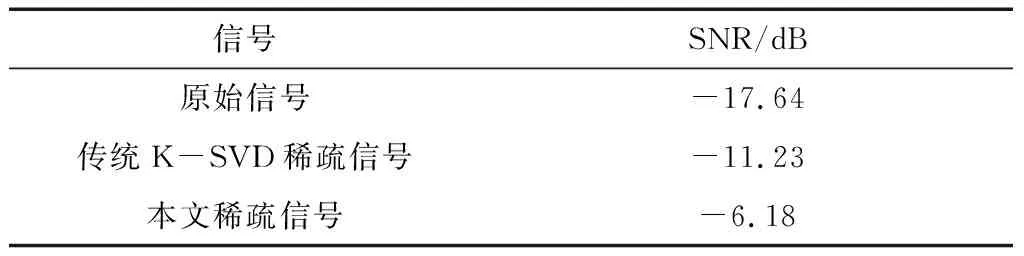
表2 各信号和SNR指标值

4 实验验证

在本节中，1组具有轴承外圈剥落故障的声音数据将被用于验证提出方法的有效性，轴承型号为6308，外圈故障频率f为61.78 Hz。该实验台包括了调速器、直流驱动电机、动力箱、滚动轴承安装架、轴向加载装置和径向加载装置等部分，如图4所示。过程中电机转速为1 200 r/min，通过麦克风采集滚动轴承的声音信号，采样频率为12 kHz，采样时间为10 s，取其中0.5 s作为分析信号。

图4 实验装置

如图5所示，图5a、图5b分别为轴承外圈故障信号时域图、包络谱图。从时域图可知，轴承外圈故障信息被环境噪声所淹没，很难看出由任何周期性冲击成分；包络谱中也无法清楚地找到轴承外圈故障特征频率。

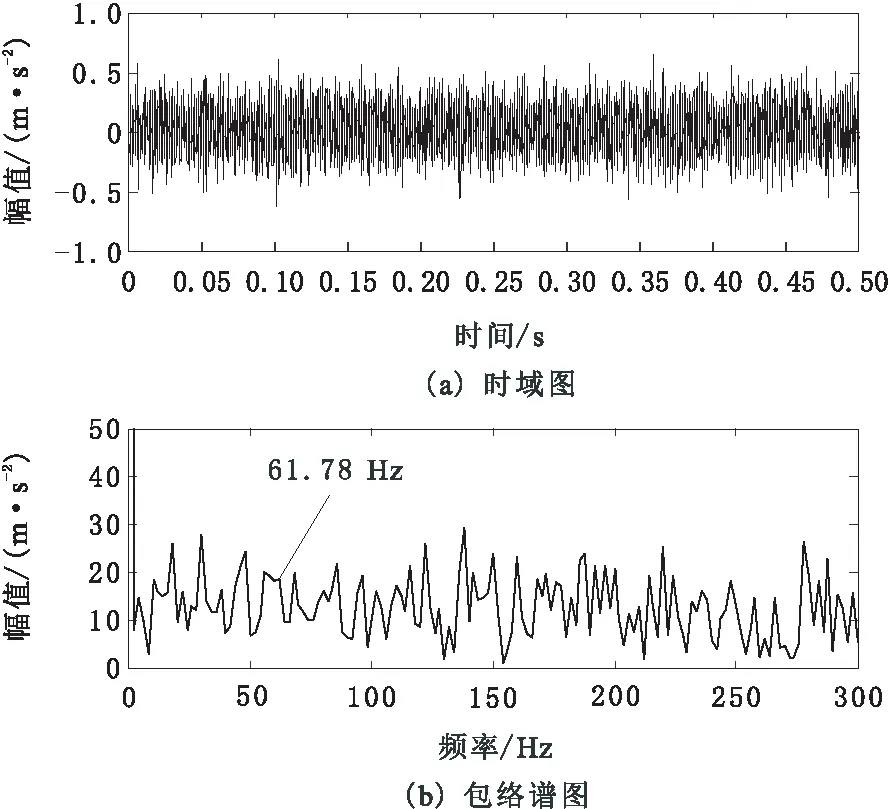
图5 外圈故障实验信号

用VMD分解该信号，得到6个IMF分量；各IMF分量SAF指标计算结果如表3所示，其中，IMF3分量SAF指标值最大，故选取IMF3作为最优IMF分量。

表3 IMF分量和SAF指标值

传统K-SVD字典学习方法和本文方法所得稀疏信号的时域图和包络谱图如图6所示。

图6 轴承外圈故障实验信号稀疏后的信号

通过对比图6a、图6c可以发现，本文方法所得稀疏信号时域图周期性冲击信息更明显，而经传统K-SVD字典学习方法得到的稀疏信号时域图含噪信号较严重。从包络谱图6b、图6d中可知，本文方法更能精准地识别轴承外圈故障特征频率f以及其倍频，且幅值更为突出。对实验所采集的声音信号分析，进一步验证了本文方法相比于传统K-SVD方法具有更好的诊断效果。

此外，分别计算轴承外圈原始声音信号、传统K-SVD字典学习方法和本文所提方法获得的稀疏信号的信噪比(SNR)，如表4所示。

表4 各信号和SNR指标值

5 结束语

针对强背景噪声下轴承早期周期性冲击故障特征提取问题，本文提出了一种基于最优IMF分量与K-SVD结合的轴承故障诊断方法。借助SAF指标自适应选取原始信号经VMD分解后的最优IMF分量，有效剔除了信号中的干扰成分；结合K-SVD字典学习方法，利用 OMP方法对原始信号进行稀疏表示获得稀疏信号，大幅度提高了信号的SNR。包络谱分析结果表明，本文方法能更精准、更清晰地识别轴承外圈故障特征频率及其倍频。仿真和实验结果表明，本文所提方法在轴承故障特征增强优于传统K-SVD字典学习方法。