被动变弦长提升变转速尾桨性能

万浩云,韩东*,张宇杭

南京航空航天大学 航空学院 直升机旋翼动力学国家级重点实验室,南京 210016

作为提升直升机飞行性能的新方式,直升机旋翼变转速技术得到了越来越多的关注。改变发动机输出轴转速是改变旋翼转速的方法之一,但同时也会改变尾桨转速。尾桨转速降低引起动压降低,导致尾桨最大拉力降低,进而降低尾桨平衡旋翼反扭矩和实施航向控制的能力。直升机高速飞行时,降低尾桨转速可能导致尾桨需用功率增加。直升机处于飞行包线边界附近,尾桨功率可达旋翼功率20%。对于变转速尾桨,有必要寻找降低需用功率和提升最大拉力的方法,以补偿尾桨转速降低对直升机飞行性能的负面影响。

为提升尾桨性能,可优化尾桨翼型、扭转角、桨叶片数、尾桨半径等参数,但参数确定后无法随直升机飞行状态改变,无法适应变转速直升机不同飞行状态。动态变弦长属于一种直升机旋翼变体技术,可用于提升直升机旋翼性能。动态变弦长需要外界输入能量进行驱动,结构较为复杂,实现难度较大。考虑到上述问题,针对变转速尾桨,本文提出一种新的被动变弦长概念,弦长随尾桨转速变化而变化,转速降低,弦长增加,最大拉力增大。这一概念兼顾常规方法与动态变弦长优势,一方面不需要外界输入额外能量,另一方面可适应变转速直升机不同飞行状态。

Léon等使用准静态变弦长来扩展旋翼飞行器的飞行包线,分析表明可达到预期效果。Khoshlahjeh和Gandhi研究了旋翼变弦长,研究结果表明,变弦长在直升机处于大总重和高海拔时可降低旋翼功率。Kang等的分析表明,变弦长可降低旋翼功率,尤其是在高速飞行时。Han等的研究表明,相同条件下,旋翼动态变弦长可比静态变弦长节省更多功率,低阶动态变弦长节省功率效果优于高阶。Han和Barakos研究了动态变弦长降低旋翼桨毂力和力矩,桨毂力降低最高可达89.4%。目前,尚未见采用本文变弦长方法用于提升变转速尾桨性能。

本文基于采用UH-60A 直升机参数验证的直升机飞行性能分析模型,建立尾桨被动变弦长模型,分析尾桨转速、变弦长伸长量对尾桨需用功率、总距和拉力的影响,讨论变弦长参数的选取以及变弦长提升尾桨性能的机理。

1 直升机建模及尾桨性能计算方法

1.1 直升机飞行性能分析模型

本文建模方法参考文献[15],直升机模型由4个部分组成,分别是旋翼动力学综合模型、机体模型、尾桨模型与前飞配平模型。旋翼模型包含中等变形梁模型、桨叶绕铰链的刚性旋转、非线性准定常空气动力学模型以及Pitt-Peters动态入流模型等。桨轴上任意点相对当地气流的速度由飞行状态和桨叶运动共同确定。桨盘平面上诱导速度利用Pitt-Peters 动态入流模型确定。叶素的气动力根据迎角和马赫数通过查表来确定。根据Hamilton 原理,考虑旋翼结构、运动、气动和控制等方面的强非线性耦合,建立基于广义力形式的旋翼动力学非线性方程。旋翼周期响应采用隐式Newmark积分法计算。

机体模型主要考虑其所受气动力和气动力矩,以体现前飞时机体模型对机身废阻功率和配平的影响。给定初始操纵量和机体姿态角值,由旋翼模型计算出旋翼桨毂力和力矩,再将桨毂力和力矩代入直升机整机的平衡方程。由整机平衡方程可求解出机身姿态角和旋翼操纵量,将这些量再重新代入旋翼模型中,这样不断地迭代直至收敛,就可得到各个状态量,从而得到旋翼的需用功率。尾桨拉力自动平衡旋翼反扭矩。

1.2 尾桨性能计算

尾桨模型基于刚体桨叶,考虑尾桨倾斜角,用于平衡旋翼反扭矩的净拉力为

式中：为尾桨拉力；为尾桨倾斜角；为垂尾引起的尾桨阻塞效应,

式中：为垂尾面积；为尾桨面积。

净拉力平衡旋翼反扭矩：

式中：为旋翼需用功率；为旋翼转速；为尾桨轴至旋翼的距离。

联立式(1)、式(3)可得尾桨拉力

尾桨总距初始值由经验公式得到：

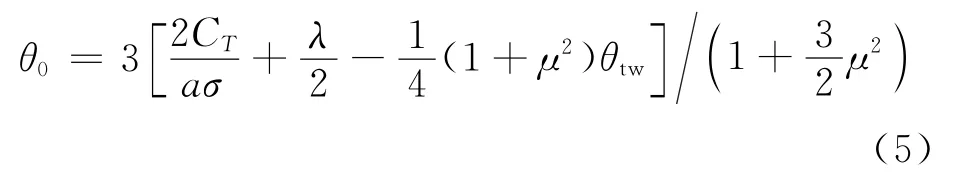
式 中：C为 尾 桨 拉 力 系 数；为 升 力 线 斜 率；为尾桨实度；为尾桨流入比；为尾桨前进比；为尾桨预扭角。

由叶素理论得到尾桨拉力和扭矩,如图1所示,直升机前飞过程中：

图1 尾桨叶素合速度与气动环境[23]Fig.1 Tail rotor blade element incident velocities and aerodynamic environment[23]

式中：为尾桨方位角；为尾桨额定转速；为尾桨径向坐标；为前飞速度；为尾桨诱导速度,按均匀流处理。

来流角为

迎角为

式中：为尾桨半径。

由合速度与当地声速可以得到马赫数,根据马赫数与迎角查二维翼型表,得到叶素的升力系数C和阻力系数C ,从而求得叶素的升力和阻力：

式中：为空气密度；为尾桨桨叶弦长。

设尾桨桨叶片数为,由距离旋转中心为处叶素的升力和阻力,得到对应尾桨拉力和扭矩微元：

沿径向和周向对尾桨拉力和扭矩微元进行数值积分可得给定尾桨总距时的拉力与扭矩：

进一步得到尾桨功率

将式(4)尾桨拉力无量纲化,得到目标尾桨拉力系数C (目标)。将式(15)尾桨拉力无量纲化,得到给定尾桨总距时的拉力系数C。二者作差后修正尾桨总距,迭代计算C,当|C-C(目标)|＜1×10时,停止迭代。

1.3 模型验证

本模型由UH-60A 直升机飞行试验数据验证。旋翼和尾桨的参数在表1和表2中列出,从直升机的质心到旋翼桨毂的垂向距离是1.78 m,机身阻力参考文献[24]。

表1 旋翼参数[25-27]Table 1 Parameters of main rotor[25-27]

表2 尾桨参数[25-27]Table 2 Parameters of tail rotor[25-27]

为直升机重量系数,分别将=0.006 5与=0.007 4 时旋翼功率系数模型预测值与UH-60A 飞行试验数据进行比较,如图2(a)所示。将相同重量系数的尾桨功率系数模型预测值与UH-60A 飞行试验数据进行比较,如图2(b)所示。对于不同的重量系数,旋翼和尾桨功率的模型预测值与飞行试验数据均吻合较好。

图2 模型预测值与飞行试验值对比Fig.2 Comparison of predictions with flight data

2 尾桨变弦长模型

2.1 变弦长

从桨叶剖面看,变弦长指附加一段可延伸后缘,如图3所示。图中,为无变弦长时,连接翼型前缘和后缘的直线段的长度；(为比值)为弦长伸长量；为展开角。

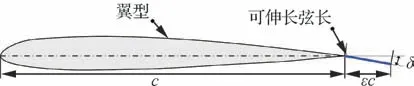
图3 桨叶变弦长剖面结构Fig.3 Configuration of extendable chord on cross section

变弦长布置于桨叶径向不同位置,如图4所示。本文中,变弦长宽度固定为10%,径向位置起始点共6个,位置1～6分别为40%、50%、60%、70%、80%和90%。

图4 桨叶变弦长径向结构Fig.4 Configuration of extendable chord in radial direction

已有研究表明,迎角为-10°～15°,马赫数为0～0.7,伸长量为0～20%时,展开角为一定数值,变弦长几乎不改变翼型气动特性。本文中,假设变弦长不改变翼型气动特性,只改变翼型弦长,进而改变桨叶剖面升力和阻力。翼型弦长改变可等效为气动力系数改变,设等效升力系数、等效阻力系数分别为¯C 和¯C ,无变弦长时升力系数、阻力系数分别为C和C ,则有

2.2 尾桨被动变弦长

已有研究中,旋翼动态变弦长指旋翼桨叶方位角变化时,弦长随之变化,需要外界输入能量进行驱动,属于主动变弦长。本文中,尾桨桨叶弦长与方位角无关,不需要外界输入额外能量,属于被动变弦长。与常规被动变弦长不同,本文中,弦长随尾桨转速变化而变化,尾桨为额定转速时,弦长伸长量为0。尾桨转速降低,弦长伸长量增加。尾桨转速降低至给定的最低值时,弦长伸长量达到最大值。

图5(a)和图5(b)分别给出了变转速尾桨被动变弦长的初始位置和任一位置。为了定量描述弦长伸长量与转速变化间的关系,作如下定义。为尾桨转速变化率,变化范围为80%～100%,如式(19)所示：

图5 被动变弦长工作原理Fig.5 Operation principle of passively extendable chord

式中：为尾桨实际转速；为尾桨额定转速,查表2知=124.6 rad/s。

配重块沿尾桨径向运动通过传动系统传递至后缘翼段,定义运动传递系数,如式(20)所示,

式中：Δ为弹簧伸长量减少量。

如图5(a)所示,初始状态下,尾桨转速为额定值,配重块处于最远径向位置,弹簧伸长量为最大值,弦长伸长量为0,配重块受弹簧拉力与离心力作用,处于平衡状态,

式中：为弹簧刚度系数；为弹簧伸长量最大值；为配重块质量；为配重块至旋转中心距离的最大值。

如图5(b)所示,尾桨转速降低后,配重块沿径向向内移动,弹簧伸长量减少,弦长伸长量增加,配重块达到新平衡状态,

联立式(21)与式(22),可得

设=100%,则有

设=80%时,=30%,可得

那么,

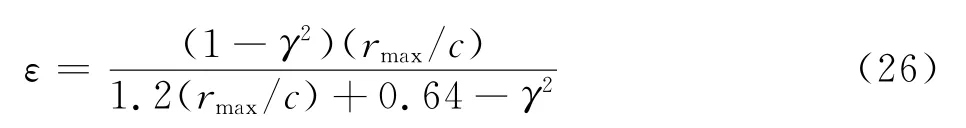
设=0.9=0.9×1.68 m=1.51 m,查

表2得=025 m,/≈6。则有

由式(27)可作曲线,如图6 所示。=90%时,可得=16.2%。

图6 尾桨弦长伸长量与转速变化率的关系Fig.6 Relationship between extendable chord length and speed change rate

上述推导结果是在给定运动传递系数、最低转速时伸长量和配重块最远径向位置的条件下得到的,条件发生改变时,伸长量与转速变化率的关系也会改变。其中,变弦长伸长量最大为30%,这一数值在现有研究中偏大。伸长量大于20%时,变弦长可能改变翼型气动特性,现有模型预测精度预计有所下降。后文中,将按照式(27),展开尾桨性能分析。

值得注意的是,本文变转速尾桨被动变弦长仅为一种概念方案,实现中会有更多动力学、结构设计、机构学等问题需要研究。

3 尾桨性能分析

直升机基准飞行状态规定为：飞行高度为海平面、起飞重量为9 474.7 kg(重量系数=0.007 4)。尾桨性能主要由尾桨需用功率体现,定义尾桨功率降低百分比,由此衡量不同变弦长布置方案的优劣：

式中：为工况改变后的尾桨功率；为基准尾桨功率。如无特殊说明,后文中基准工况均为基准飞行状态、无变弦长、额定转速。

尾桨功率降低百分比为正值时,说明尾桨功率降低,数值越大功率降低效果越好；尾桨功率降低百分比为负值时,说明尾桨功率增加,绝对值越大负面影响越大。

3.1 功 率

变弦长布置于位置4时,根据尾桨弦长伸长量与转速变化率的关系,对于不同转速和不同伸长量的尾桨,分别作前飞需用功率曲线,如图7(a)所示。根据尾桨功率降低百分比的定义,可得对应功率降低百分比曲线,如图7(b)所示。变转速对尾桨功率影响占主导地位,变弦长起辅助作用。直升机悬停状态下,尾桨变转速与变弦长对功率的影响都很小。直升机低速至中速飞行时,尾桨转速降低使功率降低,变弦长小幅减弱功率降低的效果。直升机前飞速度为190 km/h、无变弦长、尾桨转速为(==124.6 rad/s)时,功率降低百分比可达24.1%。直升机高速飞行时,尾桨转速降低导致迎角增加,失速区域扩大,尾桨需用功率大幅增加。此时,变弦长可以降低迎角,延缓失速的发生,抵消部分转速降低的负面影响。直升机前飞速度为300 km/h、无变弦长、尾桨转速为90%时,功率增加10.1%,布置变弦长后这一数值变为1.59%。

图7 不同弦长伸长量的变转速尾桨需用功率Fig.7 Variable speed tail rotor power required for different chord lengths

变弦长布置于位置4、不同前飞速度(0 km/h,150 km/h,290 km/h)时,被动变弦长降低尾桨功率效果如图8所示。图中尾桨转速由80%连续变化至100%,变弦长伸长量按照式(27)随转速一同变化。直升机前飞速度为290 km/h 时,尾桨转速降低导致功率迅速增加,弦长伸长量同时增加,增强变弦长降低功率效果。被动变弦长适应于尾桨转速降低后的气动环境,有效延缓了转速降低所导致的功率增加。无变弦长时,尾桨转速为89%,功率降低百分比为0；布置变弦长后,这一尾桨转速为84%。综上所述,被动变弦长可适应变转速直升机不同飞行状态。

图8 不同弦长伸长量的变转速尾桨功率降低百分比Fig.8 Variable speed tail rotor power reduction for different chord lengths

3.2 升阻比

直升机以300 km/h速度前飞时,无变弦长、转速为90%的尾桨升阻比分布如图9所示,高升阻比区域集中在尾桨方位角200°和340°附近。变弦长适合布置于高升阻比区域,以得到较高的工作效率。一般地,尾桨变弦长适合布置于位置4与位置5,一方面可以利用高升阻比区域,另一方面避免了后行侧升阻比极低的区域。值得注意的是,直升机高速前飞时,尾桨升阻比分布与旋翼升阻比分布完全不同,旋翼变弦长最好布置于靠近桨尖的内侧区域,以平衡其位于旋翼前行侧和后行侧的效率。

图9 尾桨桨盘升阻比分布Fig.9 Distribution of lift to drag ratio over tail rotor disk

3.3 迎 角

直升机以300 km/h速度前飞时,无变弦长、额定转速的尾桨迎角分布如图10(a)所示。前行侧的迎角明显大于后行侧,与旋翼迎角分布完全不同。尾桨因为只有总距操纵而无周期变距操纵,前行侧产生的升力远远高于后行侧。直升机以300 km/h速度前飞时,无变弦长、转速为90%的尾桨迎角分布如图10(b)所示。与图10(a)额定尾桨转速迎角分布相比,尾桨转速降低后整个桨盘区域迎角普遍增大。直升机以300 km/h速度前飞时,变弦长伸长量为16.2%,转速为9 0%的尾桨迎角分布如图10(c)所示。变弦长尾桨迎角略微减小,进而推迟气流分离和失速的发生,降低尾桨需用功率。

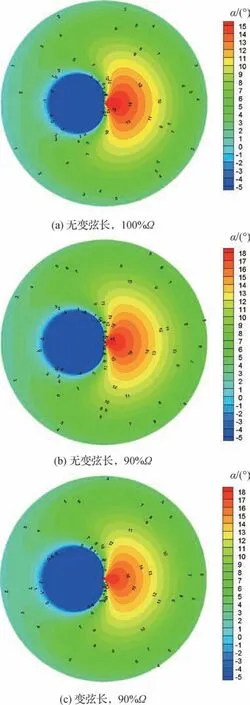
图10 尾桨桨盘迎角分布Fig.10 Distribution of angle of attack over tail rotor disk

3.4 总 距

变弦长布置于位置4时,对于不同转速和不同伸长量的尾桨,分别作总距随前飞速度变化的曲线,如图11所示。尾桨变转速对尾桨总距影响占主导地位,变弦长起辅助作用。尾桨转速降低会导致尾桨拉力降低,为了提供足够拉力,总距增加。变弦长后,尾桨总距略微降低。直升机前飞速度为290 km/h、尾桨转速为80%时,变弦长使总距下降了2.32°。

图11 不同弦长伸长量的变转速尾桨总距Fig.11 Variable speed tail rotor collective pitch for different chord lengths

3.5 拉 力

变弦长布置于位置4时,对于不同转速和不同伸长量的尾桨,分别作尾桨最大拉力随前飞速度变化的曲线,如图12所示。一般而言,直升机前飞速度增加时,尾桨最大拉力增加。变转速对尾桨最大拉力影响占主导地位,变弦长起辅助作用。尾桨转速降低引起动压降低,进而导致最大拉力降低。变弦长增大桨叶面积,进而增加尾桨最大拉力,可以补偿一部分转速降低带来的负面影响。图12给出尾桨拉力随前飞速度变化的曲线(黑色实线),尾桨拉力随前飞速度的变化规律与直升机前飞需用功率曲线一致,由式(3)可知,给定旋翼转速和尾桨桨毂中心到旋翼轴的距离,尾桨拉力直接取决于旋翼需用功率。转速降低后尾桨航向控制裕度明显减小,变弦长能使这个问题得到一定程度的改善。

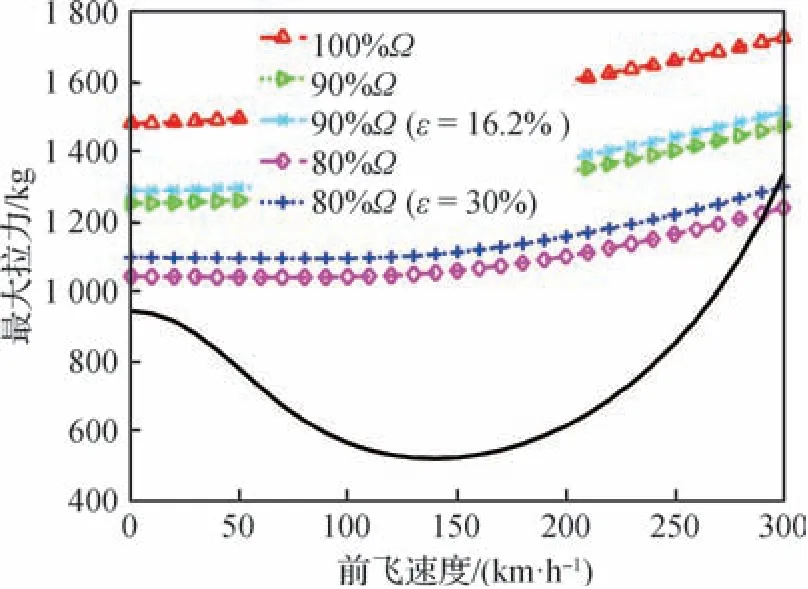
图12 不同弦长伸长量的变转速尾桨最大拉力Fig.12 Variable speed tail rotor maximum thrust for different chord lengths

3.6 径向位置

本节中,基准尾桨转速为90%,在此转速下,单独讨论变弦长对尾桨需用功率的影响。变弦长伸长量为16.2%时,作出不同位置变弦长的功率降低百分比曲线,如图13所示。直升机处于悬停状态时,变弦长对尾桨功率影响很小。直升机低速至中速飞行时变弦长会造成尾桨功率增加,变弦长布置于位置1、直升机前飞速度为180 km/h时开始起功率降低的作用,随着变弦长位置靠近桨尖,这一前飞速度逐渐变高。直升机高速飞行时,变弦长降低尾桨功率效果明显,布置于位置5时,功率降低百分比为最大值8.25%。

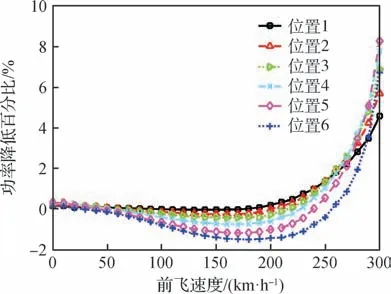
图13 不同位置变弦长的功率降低百分比Fig.13 Power reduction for different locations of extendable chord

3.7 伸长量

本节中,基准尾桨转速为90%,在此转速下,单独讨论变弦长对尾桨需用功率的影响。变弦长布置于位置5时,不同平均伸长量的功率降低百分比如图14所示。直升机悬停状态,变弦长对尾桨功率影响很小,伸长量越大,功率降低百分比越大。直升机低中速飞行状态,变弦长造成尾桨功率增加,伸长量越大,功率增加越多,前飞速度为150 km/h、伸长量为20%时,功率增加1.41%。直升机高速飞行中,伸长量越大,功率降低百分比越大,伸长量为20%时可达9.82%。

图14 不同弦长伸长量的尾桨功率降低百分比Fig.14 Tail rotor power reduction for different chord lengths

3.8 重量系数

尾桨转速为90%,变弦长布置于位置5时,直升机重量系数分别为0.006 5和0.007 4的功率降低百分比曲线如图15所示。重量系数降低,变转速尾桨功率降低百分比增加。直升机前飞速度为290 km/h,重量系数为0.007 4,无变弦长时功率降低百分比为0.843%,重量系数降低后对应数值为2.93%,同时布置变弦长后功率降低百分比为7.38%。

图15 不同重量系数的尾桨功率降低百分比Fig.15 Tail rotor power reduction for different weight coefficients

4 结 论

本文建立了直升机飞行性能分析模型,利用UH-60A 直升机飞行试验数据验证了模型正确性。提出了一种新的被动变弦长概念,建立了变转速尾桨被动变弦长模型,经过计算与性能分析,主要得出了以下结论：

1)尾桨转速降低对直升机悬停状态尾桨功率影响很小,巡航状态可使功率降低,高速飞行状态导致功率增加。直升机前飞速度为190 km/h、尾桨转速为80%时,功率降低百分比可达24.1%。

2)变转速对尾桨需用功率影响占主导地位,变弦长起辅助作用。变弦长可以抵消部分转速降低的影响,直升机前飞速度为300 km/h、无变弦长、尾桨转速为90%时,功率增加10.1%,布置变弦长后这一数值变为1.59%。直升机高速飞行时,尾桨转速降低,变弦长伸长量增加,变弦长降低尾桨功率效果增强,被动变弦长可适应变转速直升机不同飞行状态。

3)变弦长适合布置于高升阻比区域,从而得到较高的工作效率。变弦长可使尾桨迎角减小,推迟气流分离和失速的发生,降低尾桨需用功率。

4)尾桨转速降低导致尾桨拉力降低,为提供足够拉力,总距增加。变弦长后,尾桨总距略微降低。尾桨转速降低引起动压降低,进而导致最大拉力降低。变弦长可增加尾桨最大拉力,补偿一部分转速降低带来的负面影响。转速降低后尾桨航向控制裕度明显减小,变弦长能使这个问题得到一定程度的改善。

5)变弦长适合布置于尾桨半径70%～90%处。尾桨转速为90%,变弦长伸长量为16.2%,布置于尾桨半径80%～90%处,功率降低百分比可达8.25%。直升机高速飞行中,变弦长伸长量越大,功率降低百分比越大。重量系数降低,变转速尾桨功率降低百分比增加。