谐波干扰下数字化高压电能计量装置误差预补偿方法

彭录海

(国网哈尔滨供电公司，黑龙江 哈尔滨 150010)

0 引言

数字化高压电能计量装置通过光纤传输数字信号，具备自主完成信号采集与电能计量等功能，其优点为扩展性与操作性较强、信息共享率较高[1]以及抗干扰性能较优等，可有效避免二次侧电缆传输的压降误差。但在实际应用过程中，数字化高压电能计量装置会受到谐波影响，降低计量准确性[2-3]，影响电力企业与电力用户的经济效益。电力系统内因谐波导致电流与电压畸变更加严重，加剧了计量难度[4]。闫文吉等[5]研究基于二元插值算法的误差在线补偿方法，通过三次样条插值算法插值传感器输出电压，并求解各插值的计算量，完成误差补偿，提升误差补偿的实时性；郑方燕等[6]针对误差补偿精度低的问题，研究了基于遗传算法的误差补偿方法，先训练误差辨识参数的样本数据，再通过遗传算法迭代数据样本，构建误差参数的目标函数，获取误差参数的最优估计，实现误差补偿，提升误差补偿精度。但上述2种方法均未考虑谐波对误差补偿的影响，在谐波干扰下，这2种方法的误差补偿精度均较低，为此研究谐波干扰下数字化高压电能计量装置误差预补偿方法，在分析不同谐波干扰下的误差基础上，设计误差预补偿方法，进一步提高数字化高压电能计量装置的精度。

1 数字化高压电能计量装置误差预补偿方法

1.1 谐波干扰下的误差分析

数字化高压电能计量装置包含数字化乘法器与电压/频率转换器等，具体结构如图1所示。

图1 数字化高压电能计量装置结构

图1所示装置的工作步骤如下：

a.按照比例更改U与I，使变更后的U与I符合数字化乘法器可接收信号的格式。

b.利用数字化乘法器获取固定时间中的平均功率。

c.转换平均功率信号[7-8]，获取频率脉冲信号。

d.利用频率信号计数方法获取这个时间段的电量。

数字化乘法器选用时分割乘法器，在谐波干扰下，乘法器的电压信号会被分割成u1和u2，即：

u1(t)=sinω0t

(1)

u2(t)=sin 2ω0t

(2)

ω0为基波角频率；t为时间。

在标准采样频率时，g次谐波干扰下，乘法器电流ig与电压ug输入量的表达式为

(3)

Wg为g次谐波干扰下电流的有效值；ωg为谐波角频率。

(4)

Lg为g次谐波干扰下电压的有效值；δg为g次谐波干扰下电流与电压的相位差。

令调制频率为F，则在一个采样周期内基波的分割份数为

(5)

其中，f1为工频。

各等份相应的弧度为2π/m1，在g次谐波干扰下，各采样周期中[9]，分割份数为mg=m1/g。

在g次谐波干扰下，分割ig的第k份为igk，即

(6)

在g次谐波干扰下，分割ug的第k份为ugk，即

(7)

g次谐波干扰下，标准采样频率时功率值为

(8)

Pg和实际信号频率f时的功率Pgf的差为

(9)

在g次谐波干扰下，数字化高压电能计量装置的功率计量误差为

eg=(Kg-1)×100%

(10)

Kg为产生g次谐波电压的初相角。基波叠加数次谐波干扰下的计量误差为

(11)

下标0为基波分量；M为最大谐波次数。综上所述，完成不同谐波干扰次数下的数字化高压电能计量装置误差分析。

1.2 误差预补偿

以上述分析的数字化高压电能计量装置误差为基础，设计误差预补偿方法。

1.2.1 过零检测法

数字化高压电能计量装置内的采样数据按照IEC 61850协议的格式实现数据帧传输，数据帧内不存在信号的频率信息。因此，利用过零检测法求解信号频率值，提升频率测量精度，增强频率测量的实时性[10-12]。过零检测通过采样周期内邻近零点位置测量频率。令测量获取过零时刻分别是t1与t2，t1和t2间获取的信号频率为

(12)

离散采样信号的采样值不一定经过零点，因此，按照正弦信号零点邻近区域可线性化原理，求解信号过零点位置。按照正弦函数的幂级数，在信号零点邻近区域x值较小情况下，将其近似成sinx≈x。在离散采样系统内，采样点与零点邻近值趋于线性程度成正比[13]，因此，按照零点邻近的2个点求解零点位置，令零点邻近的2个点为(x1,y1)与(x2,y2)。

按照零点邻近值可线性化能够获取途径(x1,y1)与(x2,y2)的直线，公式为

(13)

设y=0，可获取零点位置为

(14)

同理，获取t2，将计算获取的t1和t2，代入式(12)计算获取f，至此完成数字化高压电能计量装置误差过零检测。

1.2.2 采样误差预补偿方法

在信号采样过程中，标准采样频率与实际采样频率不同，会造成数字化高压电能计量装置出现采样误差[14-15]，按照式(8)与1.2.1小节获取的信号实际频率，设计采样误差预补偿方法，该方法的计算流程如图2所示。

图2 误差预补偿计算流程

误差预补偿具体步骤如下：

a.在g次谐波干扰以及标准采样频率下，采集数字化乘法器的ig与ug。

b.利用式(8)求解g次谐波干扰下，标准采样频率时功率值Pg，利用过零检测算法求解该采样周期的实时信号频率f。

c.通过式(8)求解实时信号频率下的功率值Pgf，获取功率预补偿值ΔPg。

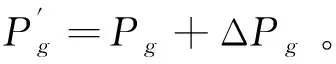
2 实验分析

以某电力系统的数字化高压电能计量装置为实验对象，通过MATLAB软件搭建三相电能计量装置，利用本文方法对该电能计量装置的误差进行预补偿，验证其有效性。利用本文方法计算不同谐波干扰次数时，该数字化高压电能计量装置的功率采样误差，计算结果如图3所示。

图3 功率采样误差

由图3可知，本文方法可有效计算谐波干扰下的功率采样误差，电能计量装置A相、B相与C相的功率采样误差整体变化趋势大致相同，均为谐波次数越多，功率采样误差越大，A相与B相的功率采样误差均在-0.000 3%～0.000 3%之间波动，C相的功率采样误差最小，在-0.000 1%至0.000 1%之间波动，在实际应用中可忽略不计。

为验证本文方法计算功率采样误差的精度，以A相为例，测试本文方法在谐波干扰次数为8次时，不同采样初始相位时的功率采样误差，并与实际功率采样误差作对比，对比结果如图4所示。

图4 功率采样误差对比结果

由图4可知，在不同采样初始相位时，功率采样误差的变化较小，本文方法计算的功率采样误差与实际功率采样误差非常接近，均在-0.000 3%～0.000 3%之间波动。实验证明：本文方法可精准计算数字化高压电能计量装置的功率采样误差，为后续误差预补偿提供精准的数据支持。

在谐波干扰次数为8次时，利用本文方法对该电能计量装置的功率采样误差进行预补偿。因C相功率采样误差非常小，可忽略不计，A相与B相功率采样误差变化趋势大致相同，因此，以A相为例，分析补偿前后A相功率变化曲线如图5所示。

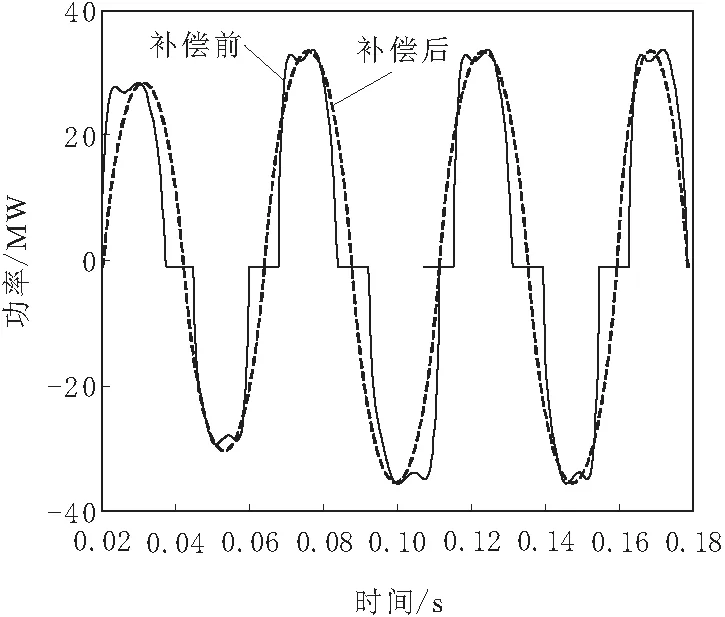
图5 A相功率采样误差补偿前后对比结果

由图5可知，误差预补偿前，A相功功率曲线连续性差，且曲线不够平滑，利用本文方法进行误差预补偿后，A相功率曲线更为平滑，且连续性好。实验证明：本文方法可有效预补偿电能计量装置的功率误差，提升功率计量精度，从而提升电能计量装置计费精度。

以A相为例，谐波干扰次数为8次，进一步验证本文方法误差预补偿效果，测试本文方法在不同实际采样频率时误差预补偿前后功率采样误差的变化情况，测试结果如表1所示。

表1 误差预补偿前后功率采样误差变化情况

由表1可知，本文方法可有效地计算实际采样频率，并且与标准采样频率相差较小，误差低于0.05 Hz；随着采样频率的降低，功率计算值与功率理论值间的误差随之增大；误差预补偿前平均功率误差为27.38%，利用本文方法误差预补偿后的平均功率误差为0.49%。因此，误差预补偿后可明显减小实际输出功率与功率理论值间的差距。实验证明：在不同采样频率时，本文方法可有效预补偿功率，缩小实际输出功率与功率理论值间的差距，为后续电能计费提供更加准确的数据支持。

在该电力系统中随机选取2个数字化高压电能计量装置，其中一个应用本文方法进行误差预补偿，记为装置1，另一个未进行误差预补偿，记为装置2，随后利用这2个计量装置记录某用户一年的报表数据，记录结果如图6所示。

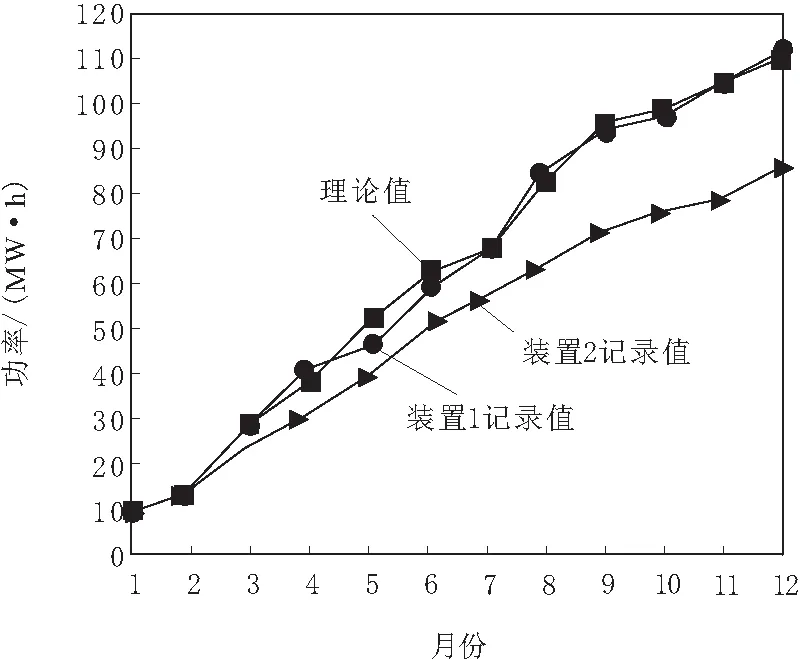
图6 报表数据记录结果

由图6可知，装置1的记录值与理论值非常接近，装置2的记录值随着时间的延长，与理论值间的差距越来越大，说明应用本文方法误差预补偿后的计量装置能够准确记录用户的报表数据。

电流回路在非高压与高压状态下，测试装置1与装置2在不同功率因数时的电能计量偏差。非高压状态功率因数为0.5与0.8时，计量装置电能计量的偏差极限为±0.6%；功率因数为1.0时，计量装置电能计量的偏差极限为±0.5%。高压状态下功率因数为0.5与0.8时，计量装置电能计量的偏差极限为±0.4%；功率因数为1.0时，计量装置电能计量偏差极限为±0.3%，测试结果如图7与图8所示。

图7 非高压状态下不同功率因数时的电能计量偏差

图8 高压状态下不同功率因数时的电能计量偏差

由图7可知，随着功率因数的增长，2个装置的电能计量偏差均呈下降趋势，在功率因数为0.5时，装置2的最大电能计量偏差正负值已超过±0.6%，说明此时该装置已不符合计量装置的标准。在功率因数为0.8与1.0时，装置2的最大电能计量偏差未超过偏差极限，说明装置2仅在功率因数为0.8与1.0时符合电能计量装置的计量要求。装置1在不同功率因数时的最大电能计量偏差均明显低于装置2，大概在±0.2%之间波动，显著低于计量装置电能计量的偏差极限，说明装置1在不同功率因数时均符合电能计量装置的计量要求。实验证明：非高压状态下，应用本文方法预补偿误差后的数字化高压电能计量装置在不同功率因数时均符合电能计量要求。

由图8可知，高压状态下装置1与装置2的电能计量偏差均低于非高压状态；在不同功率因数时，装置1的电能计量偏差均显著低于装置2；装置1在不同功率因数时的电能计量偏差均未超过偏差极限，基本控制在以内±0.1%，当功率因数为1.0时，装置1的电能计量偏差基本为0%；装置2在功率因数为0.5与0.8时，电能计量偏差已超过偏差极限±0.4%，已不符合电能计量装置的计量要求，仅在功率因数为1.0时，装置2的电能计量偏差未超过偏差极限，此时才符合电能计量装置的计量要求。实验证明：高压状态下，应用本文方法预补偿误差后的数字化高压电能计量装置在不同功率因数时均符合电能计量要求。

3 结束语

数字化高压电能计量装置包含数字化乘法器与电压/频率转换器等部分，各部分均会在谐波干扰下出现电能计量误差，影响电力用户电量统计的准确性，为此研究谐波干扰下数字化高压电能计量装置误差预补偿方法，精准补偿电能计量装置的功率误差，为用户用电性质分析与电量计费等领域提供科学依据。