一类具疫苗接种影响的2019新型冠状病毒SEIQR模型稳定性分析

李春红, 王林林, 万晶晶, 葛 静

(1. 淮阴师范学院 a. 学报编辑部, b. 数学与科学学院, 江苏 淮安 223001;2. 中国矿业大学 数学学院, 江苏 徐州 221116)

人类社会在各个不同的发展阶段,始终饱受着传染病的困扰,从某种意义上来说,人类发展史同时也是一部与传染病的抗争史。古今中外,一些大规模的传染病造成的死亡人数甚至超过了战争。1999年,世界卫生组织(WHO)在传染病的分析报告中曾指出,全世界每小时有1 500人死于传染病,从曾经的鼠疫、天花、重症急性呼吸综合征(SARS),到如今的新型冠状病毒肺炎,可以看到,传染病一直在威胁着人类的健康。传染病不断发展变化,且很难在短时间内开发出特效药,因此,预防和控制疾病的蔓延成为人们应对传染病的主要途径。18世纪中期,为了对抗天花病毒,人类历史上第一个牛痘疫苗应运而生。自人类开始接种牛痘疫苗预防天花以来,疫苗逐渐成为人们有效预防传染病的重要方法。2020年新型冠状病毒肺炎疫情迅速爆发,病毒不断变异,为了阻断病毒的进一步传播,各国科研人员正在加紧研发疫苗。截至2021年7月底,全球已经接种超过18亿剂次,此次大规模接种疫苗,对疫情的进一步蔓延起到了很好的控制作用。可见,疫苗接种率和保护力已成为疫情控制的重要因素。因此,本文将就如何利用数学模型对2019新型冠状病毒疫苗接种情况进行理论分析,从而预测其发展趋势、感染规模,并寻求控制疾病发展的最优策略进行研究。

1 模型的建立

2019新型冠状病毒在传播过程中存在一定的潜伏期,并且在潜伏期的无症状感染者具有极强的传染性[1-4]。本文将人群分为易感者、无症状感染者、有症状染病者、隔离者和移除者5类,用S,E,I,Q,R分别表示这5类人群的人数。 根据病毒的传播规律,建立如下数学模型:

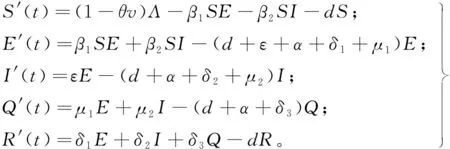
(1)

式中:ν表示疫苗接种率;θ表示疫苗的保护力;Λ表示易感人群的常数输入率;d表示自然死亡率;δ1,δ2,δ3分别表示无症状感染者,染病者和隔离者的恢复率;β1表示无症状感染者与易感者之间的接触传播率;β2表示染病者与易感者之间的接触传播率;ε表示无症状感染者转化为染病者的比率;α表示无症状感染者,染病者和隔离类的因病死亡率;μ1表示无症状感染者被隔离的比率;μ2表示染病者被隔离的比率。 从传染病学角度考虑,本文参数都是非负的实数。

将模型(1)中的5个方程相加可得

取上极限得

故模型(1)正向不变集是

2 平衡点存在性

基本再生数是指在没有干预的情况下,在全部是易感人群的环境中,平均一个患者在一个染病周期里可以传染的人数,也就是在自由传播时一个患者平均能感染多少人。在传染病学上基本再生数是评估疾病传染性的关键阈值。由下一代感染矩阵方法可推导模型(1)基本再生数[5-6]

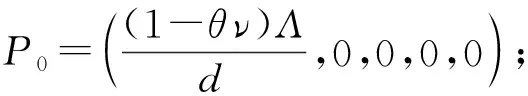
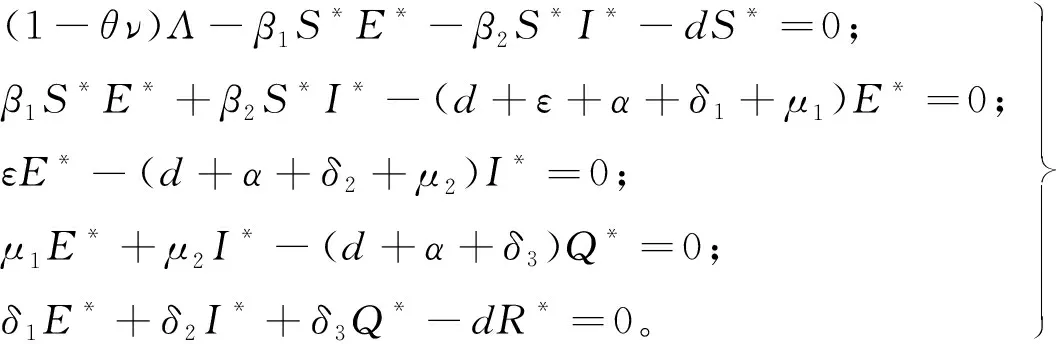
(2)

解之得:

当R0>1时I*>0,S*>0,E*>0,Q*>0,R*>0,所以模型(1)存在唯一的染病平衡点P*=(S*,E*,I*,Q*,R*),定理得证。

3 平衡点稳定性

定理1 当R0<1时,无病平衡点P0局部渐近稳定;当R0>1时,无病平衡点P0不稳定。

设其特征方程的特征根为λ1,λ2,则λ1,λ2满足方程

λ2+q1λ+q2=0。

(3)

式中:

且λ1,λ2满足

由Routh-Hurwitz判据可知,当R0<1时,无病平衡点P0局部渐近稳定;当R0>1,λ1λ2<0时,方程(3)存在一个正根,故无病平衡点P0不稳定。

定理2 当R0<1时,无病平衡点P0全局渐近稳定。

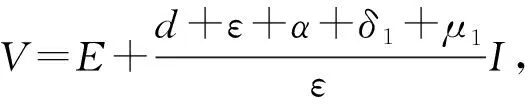
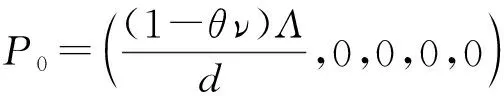
接下来考虑染病平衡点的稳定性。

易知系统(1)的前3个方程在整个系统中相对独立,考虑如下子系统:

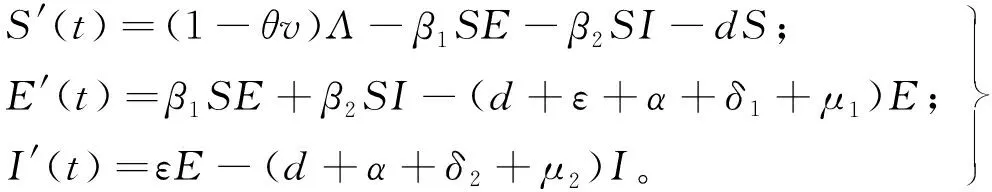
(4)

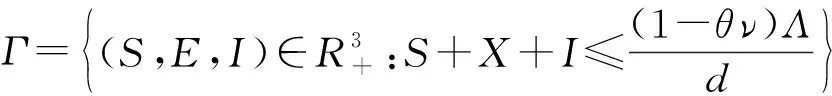
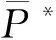
令p=β1E*+β2I*,m=d+ε+α+δ1+μ1,n=d+α+δ2+μ2,矩阵的特征方程为

式中:

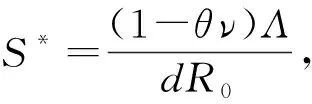
又因为-mnd+(β1(1-θν)Λn+β2(1-θν)Λε)S*d=0,故

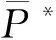
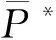
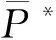
证明 系统(4)的Jacobian矩阵为

式中:m=d+ε+α+δ1+μ1,n=d+α+δ2+μ2,其对应的第二加性的矩阵为

取

矩阵B=PfP-1+PJ[2]P-1可以写成分块矩阵

式中:

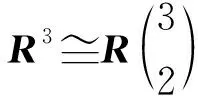
则

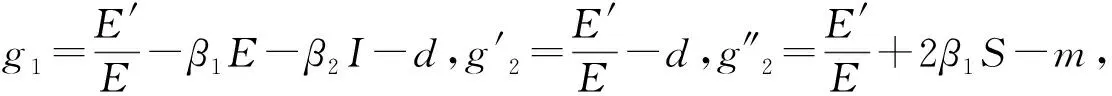
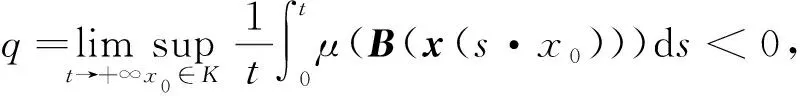
定理5 当R0>1时,模型(1)染病平衡点P*(S*,E*,I*,Q*,R*)是全局渐近稳定的。

证明 由定理4可知,当t→+∞时,(S,E,I)→(S*,E*,I*),由模型(1)的极限系统

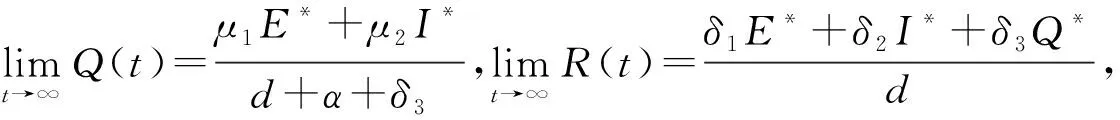
4 结 论