Sparse parameter identification of stochastic dynamical systems

Wenxiao Zhao

Sparsity of a parameter vector in stochastic dynamic systems and precise reconstruction of its zero and nonzero elements appear in many areas including systems and control [1–4],signal processing [5,6], statistics [7,8], and machine learning[9,10]since it provides a way to discover a parsimonious model that leads to more reliable and robust prediction.Classical system identification theory has been a well-developed field[11,12].It usually characterizes the identification error between the estimates and the unknown parameters using different criteria such as randomness of noises, frequency domain sample data,and uncertainty bound of system,so that consistency,convergence rate,and asymptotical normality of estimates can be established as the number of data points goes to infinity.However,these theory and methods are ill suited for sparse identification if the dimension of the unknown parameter vector is high.

Over the last few years, considerable progress has been made in the precise reconstruction of the zero and nonzero elements in an unknown sparse parameter vector of a stochastic dynamical system,for example,the compressed sensing(CS)-based identification methods[13]and the corresponding adaptive/online algorithms [14], the algorithms from statistics[7,8]and machine learning[9,10].

ThebasicideaofCStheoryistoobtainasparsestestimates of the parameter vector by minimizing theL0norm, i.e.,the number of nonzero elements,withL2constraints[5,15].The computational complexity for solvingL0minimization problem is NP-hard in general,which leads to replacingL0norm withL1norm,which can be effectively solved by convex optimization techniques. In [16], the gap betweenL0norm andL1norm is bridged and anLq-penalized least squares algorithm with 0＜q ＜1 is proposed for matrix completion.Combining these idea and the dynamics of systems,in[4,13,17],the CS method is applied to the parameter estimation of linear systems and in[14,18,19],the adaptive algorithms such as least mean square (LMS), Kalman filtering(KF),expectation maximization(EM),and projection operator are introduced.In the above literature,the measurements are usually required to satisfy the so-called restricted isometry property(RIP)condition.

In machine learning, there have also been many studies related to sparsity recovery,such as feature selection[20–22],sparsity of neural networks [23,24], and sparse solution of empirical risk minimization[25,26].In the above literature,the random signals are usually assumed to be independent and identically distributed(i.i.d.),stationary,or with a priori knowledge on the sample probability distribution.

In statistics,there are also topics approaching the problem of sparsity recovery. For example, the purpose of variable selection is to find the true but sparse contributing variables among the many alternative ones. Classical variable selection algorithms include least absolute shrinkage and selection operator (LASSO) [27] and its variants [8], least angle regression(LARS)[28],the kernel method[29],sequentially thresholded least squares(STLS)[30],etc.Considering the fact that in many scenarios the contributing variables tend to cluster in groups,in[31]the group sparse problems are studied.Most of the above literature focuses on variable selection inalinearsetting.Thenonlinearvariableselectionalgorithms can be found in[32–34],etc.

In recent years,in systems and control area there is a growing attention on adopting the sparsity recovery methodology into the identification issue of dynamical systems.In[4],the sparse identification of linear systems or parametric orthogonal rational functions is considered,and in[35]the sparse variable selection of stochastic nonlinear systems is investigated.

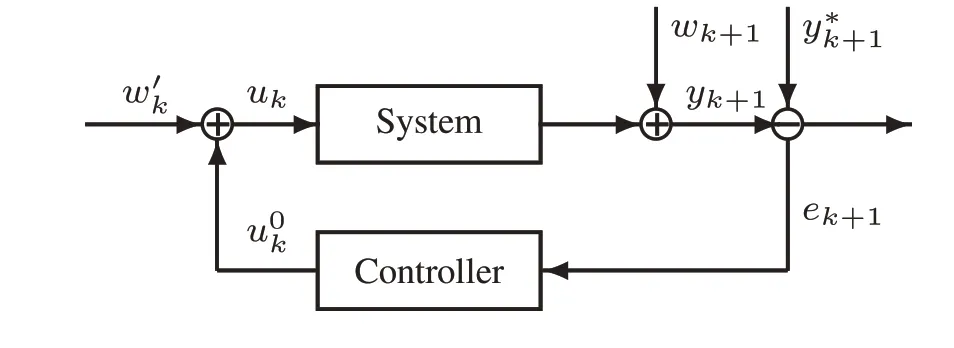
Fig.1 Flow diagram of stochastic feedback control system

Although there have been many studies on the sparse recovery problem,to the author’s knowledge,there is no consistent result for sparse parameter identification of stochastic systems with feedback control,which plays a important role in systems and control field, and in such a case, the measurements may be non-stationary.See,e.g.,Fig.1.Here the framework in Fig.1 is not confined to specific types of feedback control law, such as PID control, adaptive regulation control, or model reference control, but in a general form.That is,the control inputuk+1belongs to theσ-algebraFk+1generated by the past system inputs, outputs, noises, and exogenous dithers.

Consider the parameter identification of the following stochastic system:

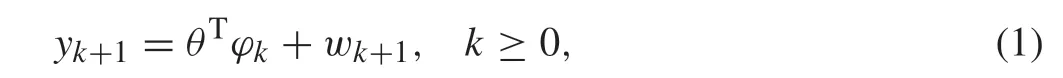
whereθis the unknownr-dimensional parameter vector,φk∈Rr, withrbeing known consisting possibly current and past inputs and outputs,is the regressor vector,yk+1andwk+1are the system output and noise, respectively. Moreover,denote the parameter vectorθand the index set of its zero elements by

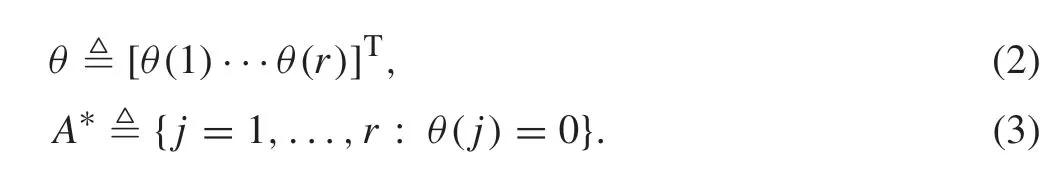
By assuming that the regressorφkisFk-measurable for eachk≥1, the problem is to infer the setA*and to estimate the unknown but nonzero elements inθbased on the system observations{φk,yk+1}Nk=1.In[36],a sparse parameter identification algorithm is proposed, which is based onL2estimation error withL1regularization. The key difference between the proposed algorithm and those in CS and LASSO framework lies in that weighting coefficients generated from the data of closed-loop systems are introduced to each of the optimization variables in theL1term. Under a general excitation condition on the system including feedback control it is proved that estimates generated from the algorithms have both set and parameter convergence,that is,sets of the zero and nonzero elements in the unknown sparse parameter vector can be identified with probability one with a finite number of observations,which is different from the asymptotical theory in the classical system identification literature,and furthermore,estimates of the nonzero ones converge to the true values almost surely.In[36]it is also shown that the usual persistent excitation(PE)condition for system identification [12] and irrepresentable conditions for consistency of LASSO[8],are not required.

Recently,there is a strong tendency in literature combining the ideas from signal processing,machine learning,etc.,with the problems in systems and control.On the other hand,how to use these cutting-edge methodology to cope with the frontier problems in systems and control,such as sparse identification, distributed optimization, etc., has just begun and is deserved for future research.