Adaptive robust simultaneous stabilization of multiple n-degree-of-freedom robot systems

Haiying Zhang·Renming Yang

Abstract In this paper,the adaptive robust simultaneous stabilization problem of uncertain multiple n-degree-of-freedom(n-DOF)robot systems is studied using the Hamiltonian function method,and the corresponding adaptive L2 controller is designed.First,we investigate the adaptive simultaneous stabilization problem of uncertain multiple n-DOF robot systems without external disturbance.Namely,the single uncertain n-DOF robot system is transformed into an equivalent Hamiltonian form using the unified partial derivative operator(UP-DO)and potential energy shaping method,and then a high dimensional Hamiltonian system for multiple uncertain robot systems is obtained by applying augmented dimension technology,and a single output feedback controller is designed to ensure the simultaneous stabilization for the higher dimensional Hamiltonian system.On this basis,we further study the adaptive robust simultaneous stabilization control problem for the uncertain multiple n-DOF robot systems with external disturbances, and design an adaptive robust simultaneous stabilization controller. Finally, the simulation results show that the adaptive robust simultaneous stabilization controller designed in this paper is very effective in stabilizing multi-robot systems at the same time.

Keywords Multiple robot systems·Adaptive robust control·Simultaneous stabilization·Hamiltonian function method

1 Introduction

With the development of artificial intelligence technology,the application of robots is becoming more and more common in real life.Meantime,it also brings many key problems that need to be solved urgently such as non-linear modeling,robust control and observer-based control[1–8],etc.Among them, the robust control problem is an important issue in robot system control [5–7].In fact, as a kind of actual system,it is inevitable to encounter many uncertain factors and interferences, which affect the control performance of the robot system. Therefore, how to deal with the uncertainty and interference problems in robot system control has been a hot issue[5–7].In[5],a robust adaptive fuzzy neural control (AFNC) method was proposed, by which the authors effectively solved the motion control problem of multi-link robot manipulators.In[6],the robust control of multi-robot systems was studied by applying distributed method, and a corresponding control strategy was presented. By using Bernstein polynomials as universal approximator,Alireza[7]designed a robust adaptive controller for electrically driven robots.

It should be pointed out that,in the production of modern enterprises,it is almost impossible for a single robot to complete complex and tedious tasks, and thus the multi-robot joint operation came into being [6,9]. Compared with single robot system, multi-robot systems have the advantages of strong robustness,low cost,high work efficiency,and less redundancy [9] and so on. In the case of multi-robot joint operations,one needs to design its robust controller for the multi-robot systems. However, in practical applications, it is expensive to design controllers for each robot system in multi-robot systems,and the control effect is not ideal,which can be seen in the simulation part of the paper below(Further details,also see[9]).Therefore,it is an inevitable choice to design its simultaneous stabilization controller.As the name suggests, the simultaneous stabilization means designing a single controller to stabilize multiple systems at the same time.

In the past few decades, the simultaneous stabilization problem has attracted the attention of many scholars, and some better results have been obtained [10–16]. Blondel[10]and Howitt[11]studied the simultaneous stabilization problem of linear systems. In [10], the authors presented a series of effective simultaneous stabilization control results on linear system.In[11],a necessary and sufficient condition on the simultaneous stabilization was presented for singleinput linear systems by designing a linear state feedback controller.In the recent research[12–16],the authors investigated the simultaneous stabilization problem of nonlinear systems.Cai[12,13]gave the adaptive and robust simultaneous stabilization results for nonlinear systems respectively.Dastaviz[14]studied the discrete sliding mode simultaneous stabilization problem of a class of uncertain discrete-time systems with time-varying state delays.In[15]and[16],the authors studied the simultaneous stability problem for the Hamiltonian systems with disturbances.However,the aforementioned results are either linear systems,linear main part systems or special nonlinear systems,and they are not actual robot systems mainly because there are not effective research methods for the real robot systems.

As well known,the Hamiltonian method plays an important role in studying real systems, because, on one hand,many actual models such as physical science and aerospace science appear in the Hamiltonian form[17–21],and on the other hand, a Hamiltonian function is usually chosen as a candidate Lyapunov function of some real systems.Furthermore,there are many mature design methods in studying the Hamiltonian system and many nonlinear control problems have been successfully solved by using the method[15–20].In view of these,in[17],the authors extended the Hamiltonian method to investigate a single robot system,successfully presented a Hamiltonian form of the robot system,and given several robust stabilization results on the system. In [21],the author studied the simultaneous stabilization problem of nonlinear systems by using the Hamiltonian function method anddesignedthefinite-timerobustsimultaneousstabilization controller for a class of nonlinear time-delay systems.However, according to our knowledge, there is almost no result on the adaptive robust simultaneous stabilization problem for multi-robot systems,which motivated the present paper.

In this paper, we investigate a set of robot systems with uncertain and external disturbance via the Hamiltonian function method, and give several adaptive and robust adaptive control results.The main contributions are as follows:1)Differentfrom[17],thispresentpaperstudiestheadaptiverobust simultaneous stabilization problem of multiple robot systems instead of the adaptive robust control problem for a single robot system in[17].2)Different from the simultaneous stabilization results obtained in[12],this present paper studies a group of actual robot systems with uncertain and external disturbance rather than the pure theoretical ones studied in[12].In fact,compared with the pure theoretical system,the practical engineering system is more complicated and some ideal conditions are not met.Moreover,the above mentioned results are not adaptive robust control ones.3)In[6],the authors investigated the control problem of multi-robot systems.However,Zhou[6]used the distributed algorithm,and developed some results on the path planning problem to avoid robot collision for multi-robot systems. While the present paper studies adaptive robust simultaneous stabilization problem of unknown multi-robot systems by using the Hamiltonian function method,and presents several adaptive(robust)simultaneous stabilization control results,which are different from[6].

2 Problem formulation and preliminaries

Considering an uncertainn-DOF robot system,its joint space dynamic equation is described as[17]

whereG0(q)∈Rnstands for the nominal part ofG(q),θis the unknown vector in the uncertain part ofG(q).

Remark 2Similar to [17,22], we have introduced Assumption 1. In fact, this assumption holds for the actual robot systems in [17,22,23], and the simulation example in this paper.Further details,please see[22].

wherex∈ Rnis the state variable, the Hamilton functionH(x)represents the generalized total energy of the system,u, yare the input-output variables with appropriate dimensions,J(x)∈Rn×nis an anti-symmetric matrix,R(x)∈Rn×n≥0 is a symmetric positive semi-definite matrix, which represents the dissipation of the system, andg(x)∈Rn×nis a weighted coefficient matrix.

Now,we use the energy shaping method to transform system(1)into its Hamiltonian form.To do this,consider system(1),and construct the following Hamiltonian function:

whereK D=K DT(K D∈Rn×n)is a constant positive definite matrix,anduis the new control input.

According to the formulas(11),(12),(13),(14)and(15),we have

whereQis a nonnegative matrix.

From the inequality(19),it is easy to obtain the following properties:

P1.Forw/=0,L2gain fromwtozis less thanγ.

P2. Whenw= 0, the closed-loop system is Lyapunov stable.Furthermore,ifQ/=0,that is,Qis positive definite,then the closed-loop system is asymptotically stable.

Now, according to the above definition, we study the interference suppression problem of the robot dissipative Hamiltonian system.

From (17), system (18) can be transformed into the following Hamiltonian form:

wherew∈Rn,g1(x)= ¯g1(x)= [0,InT,0]T∈R(2n+l)×n,and the other quantities are the same as formula(17).

Moreover,the following γ-dissipative inequality holds along the trajectory of the closed-loop system composed of equations(20)and(22):

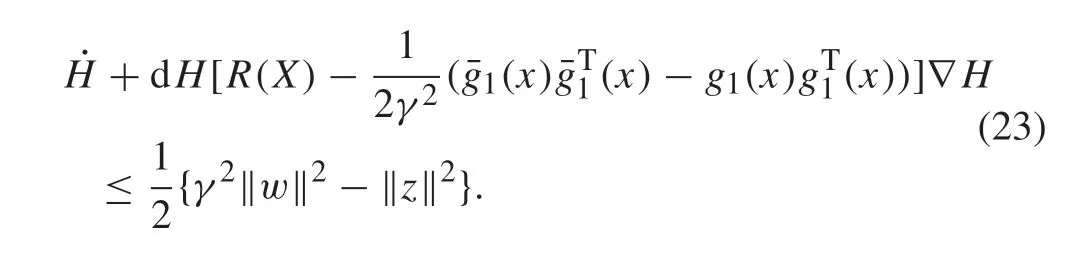
3 Main results

The section will give the main results of the paper. To facilitate the reader,in this section,we divide into two subsections,namely,Sects.3.1 and 3.2.In Sect.3.1,we design an adaptive simultaneous stabilization controller for uncertain multi-robot systems without external disturbance,while in Sect.3.2,we further present the adaptive robust simultaneous stabilization control result for the uncertain multi-robot systems with the external disturbance.

3.1 Adaptive simultaneous stabilization

In this section, we first present the adaptive simultaneous stabilization result of two uncertainn-DOF robot systems,and on the basis,give the adaptive simultaneous stabilization result on the multiple uncertainn-DOF robot systems. To do this, consider the following two uncertainn-DOF robot systems[17,23]:

ProofSubstituting(28)into the systems(25)and(26),one can obtain that

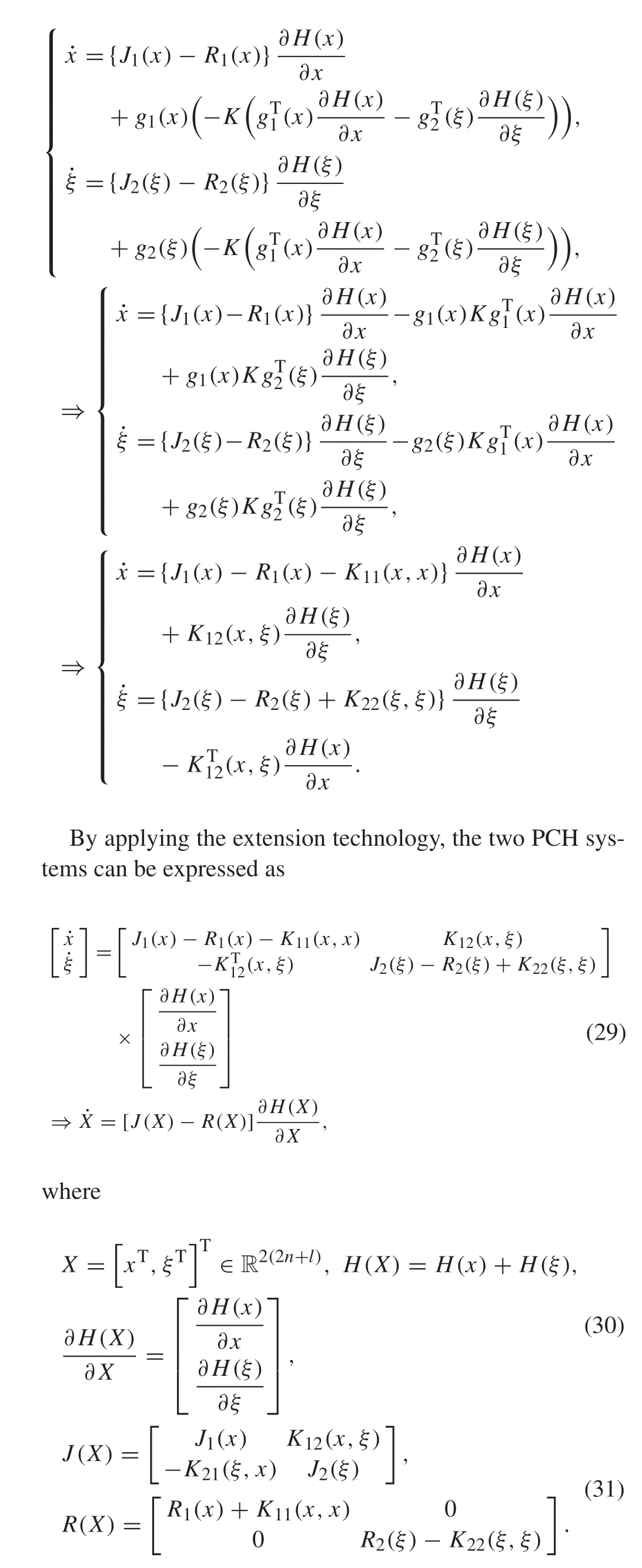
Note thatK21(ξ,x)=K(x,ξ),soJ(X)is antisymmetric and from equation (27),R(X)is semi-positive definite.Therefore, system (29) is an extended dissipative Hamiltonian system.From the properties of dissipative Hamiltonian system,system(29)is stable.Next,consider the energy flow of the system,from formula(29),we can obtain that

Theorem 2Assume that there exists a symmetric matrix K∈Rn×n with appropriate dimension, any permutation(i1,i2,...,iN) of1,2,... and N, and a positive integer L(1 ≤L≤N-1)such that

can simultaneously stabilize N uncertain robot Hamiltonian systems given in formula(32),whereˆθi is the estimate of θi in the ith system.

ProofThe proof is similar to Theorem 1,and thus is omitted.

Remark 5The purpose of designing the controllers(28)and(36) is, by applying the controllers, one can build relationships between subsystems, and also get an antisymmetric matrix form.Thanks to the form,the paper presents two concise results in Theorem 1 and 2 (Further details, also see Conditions (27) and (35)), which is also an advantage of using Hamiltonian function method in the paper.

3.2 Robust adaptive simultaneous stabilization

Under the external disturbanceω, the section presents the robust adaptive simultaneous stabilization results on the two systems (25) and (26), and the multi-systems (32) respectively.

Consider the systems(25)and(26)with the external interferenceωas follows:

as the penalty signal of the systems withΛ∈Rn×nbeing a weighted matrix.

The robust adaptive simultaneous stabilization problem is to design an output feedbackL2interference suppression controller such that,under the controller,

R1. Whenw= 0, system (37) and system (38) can be stabilized simultaneously.

R2.TheL2gain(fromωtoz)of the closed-loop system is not greater than the givenγ.

According to the above, we have the following main results.

as penalty signal,whereΛ∈Rn×nis a weighted matrix.

In this section,our design objectives are as follows:design an output feedbackL2interference suppression controller such that,under the action of the controller,

R1’.Whenw=0,NHamiltonian systems given by equation(50)are simultaneously asymptotically stable.

R2’. TheL2gain (fromωtoz) of the corresponding closed-loop system is not greater than the givenγ.

Suppose(i1,i2,...,iN)isanypermutationof1,2,...,NandLis an integer satisfying 1 ≤L≤N- 1. Let other parameters are the same as formula(33)and formula(34).

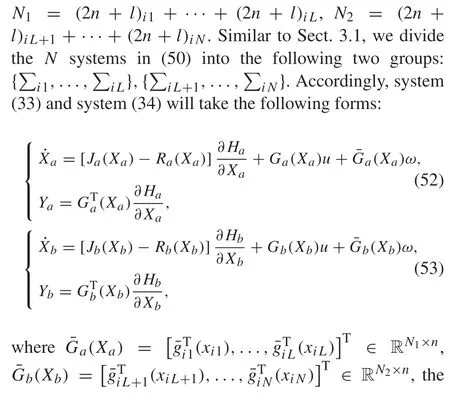
For the robust adaptive simultaneous stabilization ofNuncertain robot Hamiltonian systems in (50), we give the following results.

is an adaptive L2interference suppression controller.

ProofSimilar to Theorem 3,one can get the conclusion.

Remark 6Different from Sect. 3.1, this section presents two more practical results for uncertain multi-robot systems mainly because the external disturbances are inevitable for real systems.

4 Simulation example

This section gives a specific example to show how to use the results obtained in the paper to design a robust adaptive simultaneous stabilization controller.

To do this,we consider two uncertain robot systems,and similar to [23], choose two 2-DOF flat mechanical arms(Note: For multiple robot systems with multiple DOF, one can handle similarly).Their schematic diagrams are shown in Figs.1 and 2,wheremai,mbiare the mass of the connecting rods of the mechanical arm a and b,respectively;lai,lbiare the length of the mechanical arm a and b connecting rods,respectively;laci,lbciare the distance between the mechanical arm a and b joints and the connecting rod’s center of gravity,respectively;Jai,Jbiare the rotational inertia of the mechanical arm a and b connecting rod,respectively,wherei= 1,2.The counterclockwise direction is specified as the forward direction of the mechanical arm. Here we assume that the massm p1 andm p2 of the object grasped by two manipulators are unknown.

Fig.1 2-DOF flat mechanical arm a

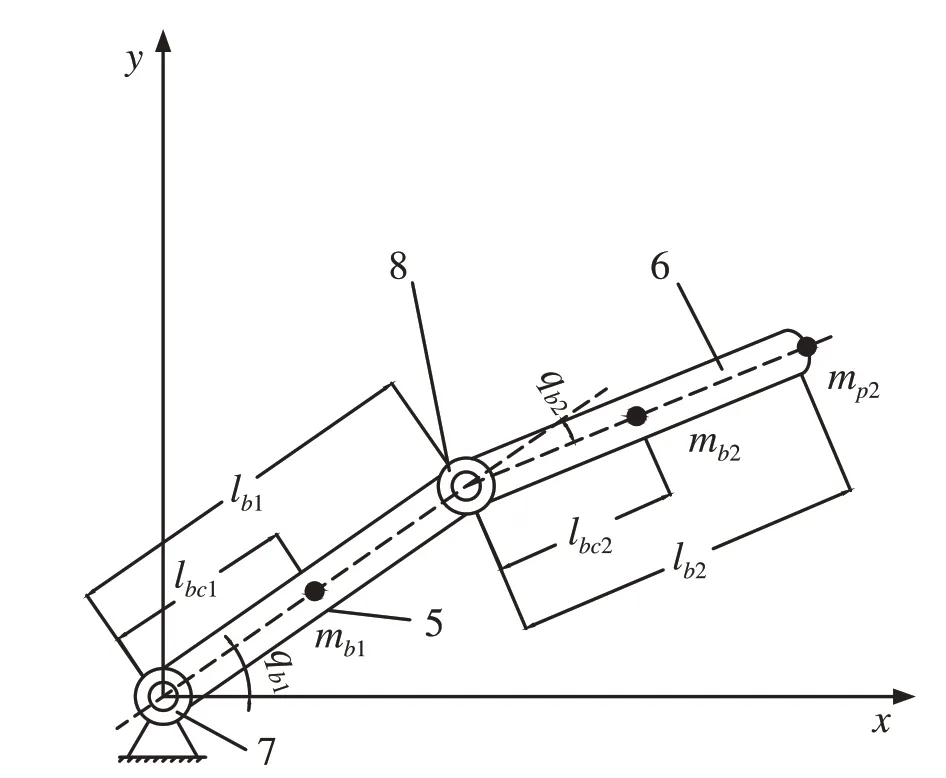
Fig.2 2-DOF flat mechanical arm b

From[23],the dynamic equations of the two 2-DOF flat mechanical arms are described as follows:

Next, to provide a dissipative Hamiltonian structure for system(56),the pre-feedback law is designed as follows:

The control parameters are chosen as follows:Λa=diag{λa1,λa2} = diag{100,100},Λb= {λb1,λb2} =diag{100,100},K Da= diag{kda1,kda2} = diag{4,4},K Db= diag{kdb1,kdb2}= diag{6,2},K= diag{k1,k2} =diag{1,-1},Λ= diag{λ1,λ2} = diag{0.2,0.3},Γa0=λa0= 100,Γb0=λb0= 100. To verify the robustness of the controller,a disturbance of amplitude[9 7]Tis added to the system within the time period 0.6–0.8s.The simulation results are shown in Figs.3,4,5,6,7,8,9,10,11,12,13 and 14.

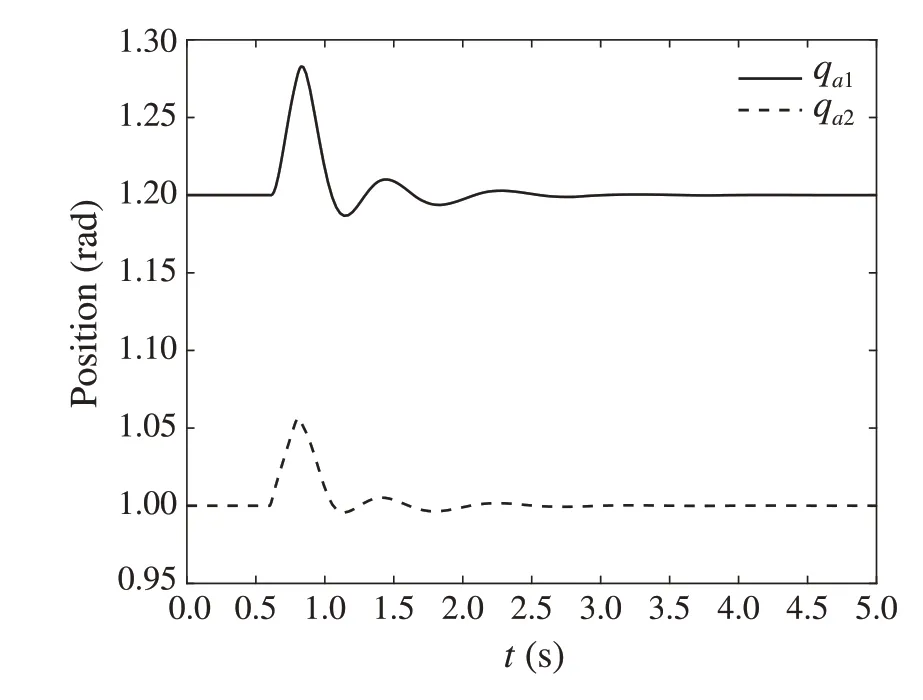
Fig.3 The angle displacement of the mechanical arm a in X0(1)

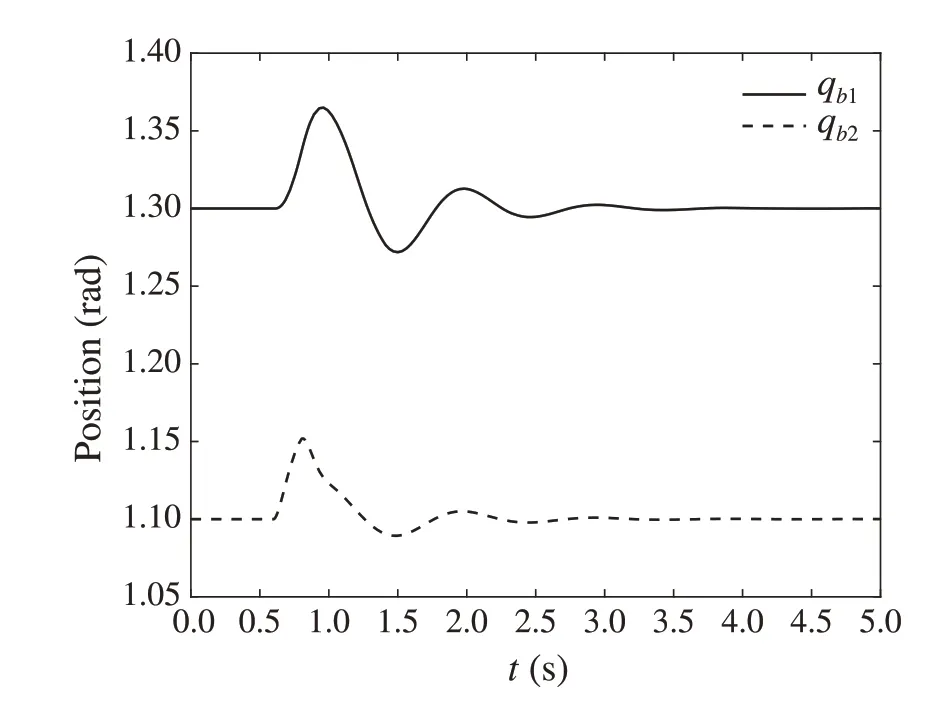
Fig.4 The angle displacement of the mechanical arm b in X0(1)

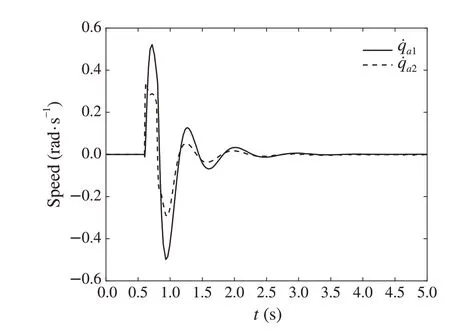
Fig.5 The angle velocity of the mechanical arm a in X0(1)

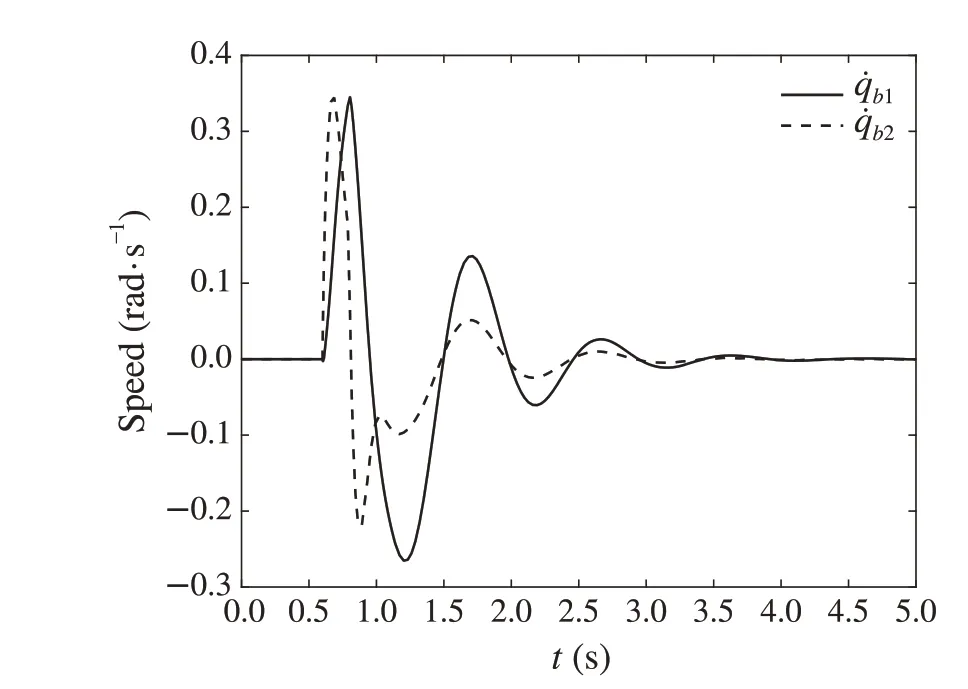
Fig.6 The angle velocity of the mechanical arm b in X0(1)

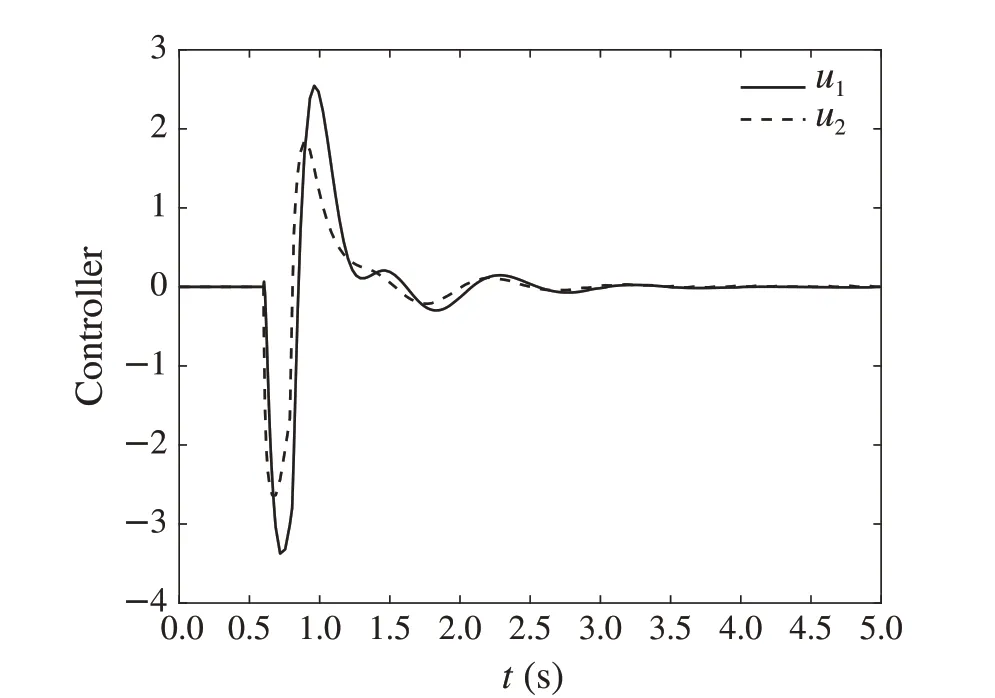
Fig.7 Control curve in X0(1)

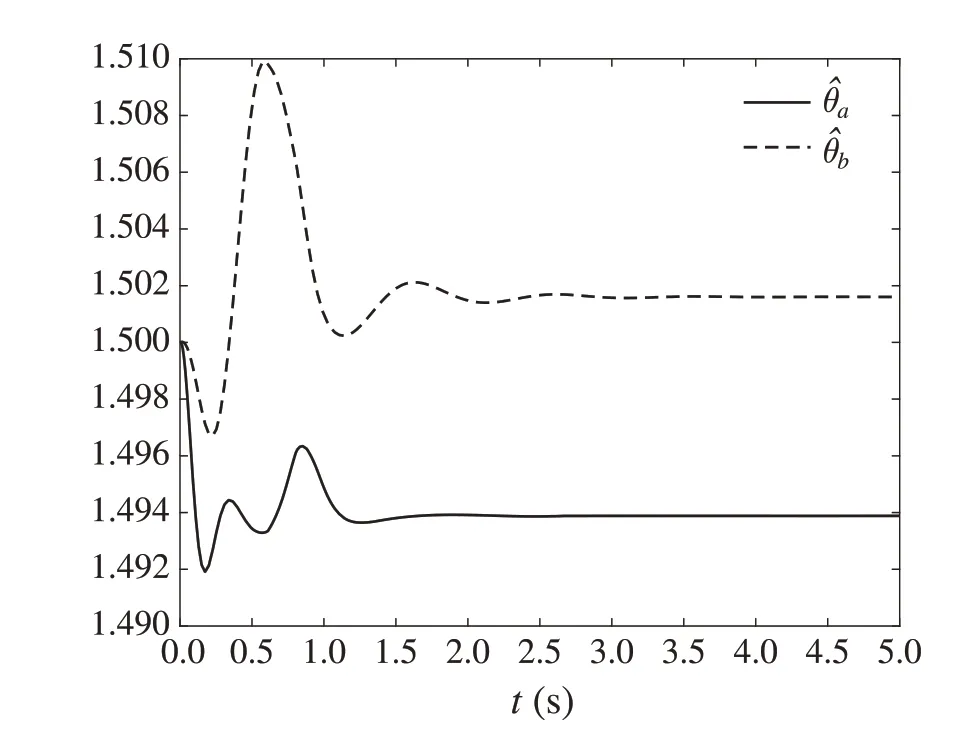
Fig.8 Curve of θˆi(i =a,b)in X0(1)

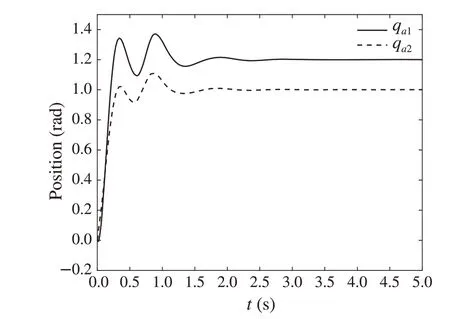
Fig.9 The angle displacement of the mechanical arm a in

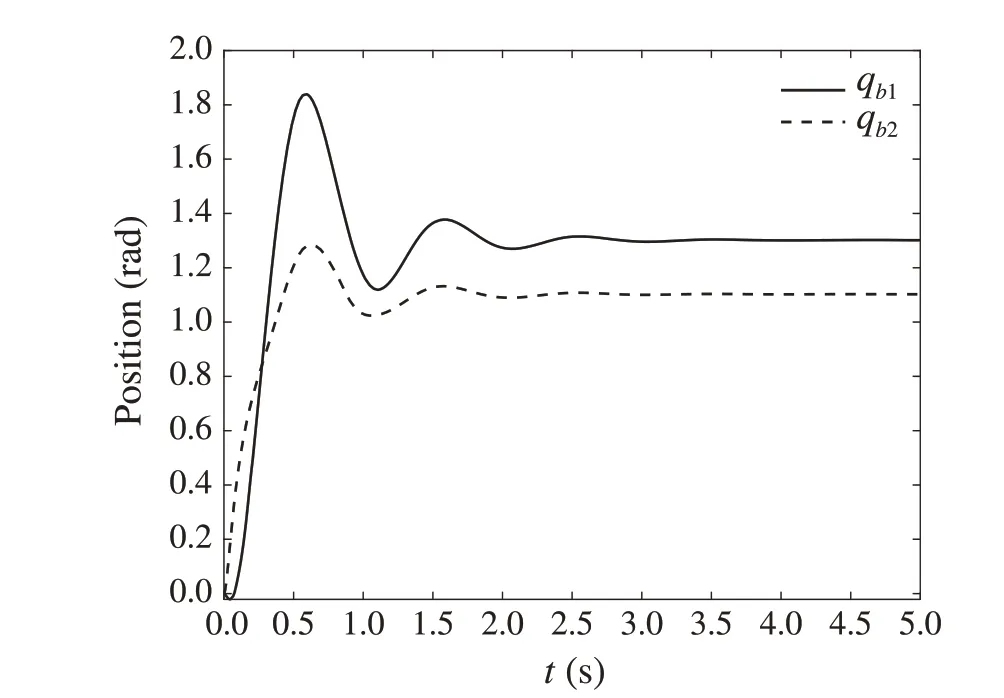
Fig.10 The angle displacement of the mechanical arm b in

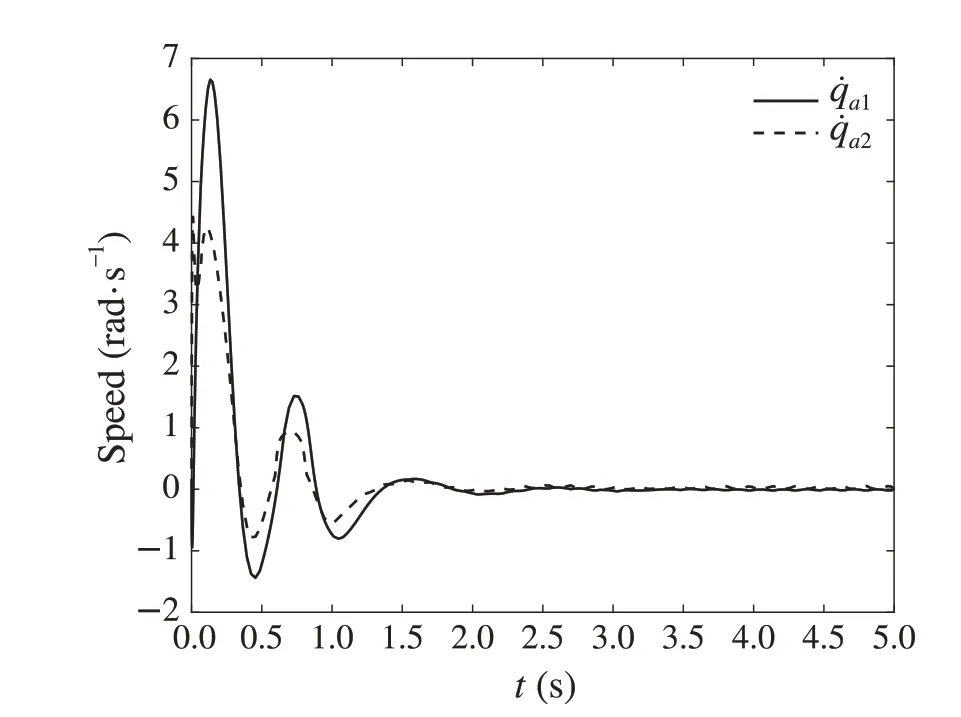
Fig.11 The angle velocity of the mechanical arm a in

To highlight the effect of the simultaneous stabilization controller (63) designed in this paper, we choose the same model parameters and simulation parameters and give the comparison results of designing independent controllers for each mechanical arm system. The simulation results are shown in Figs.15 and 16.

Fig.12 The angle velocity of the mechanical arm b in

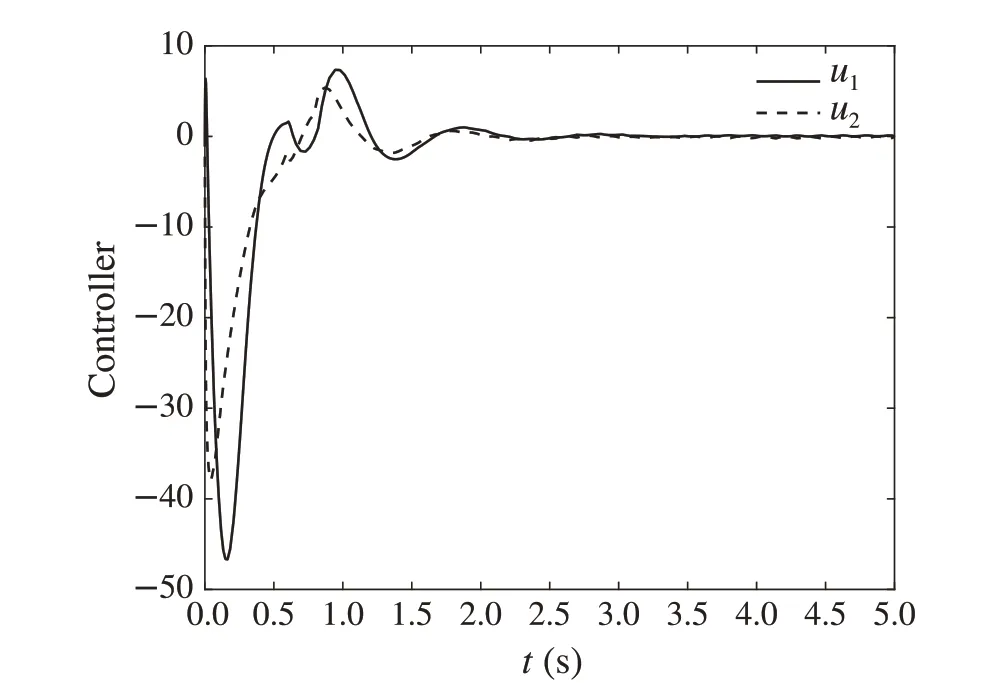
Fig.13 Control curve in

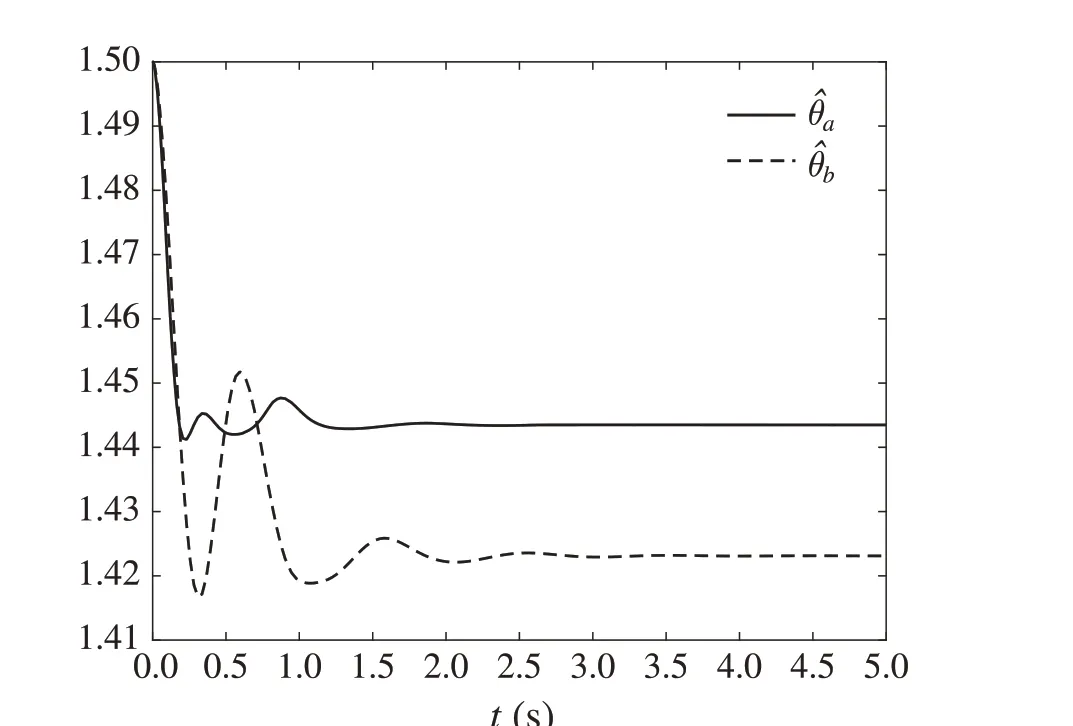
Fig.14 Curve of θˆi(i =a,b)in

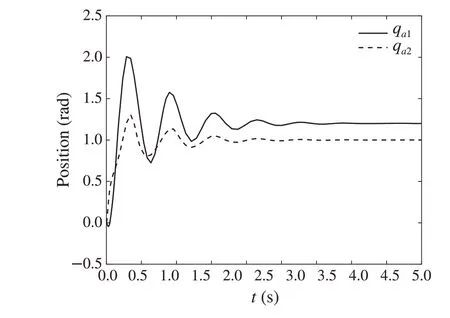
Fig.15 The angle displacement of the mechanical arm a

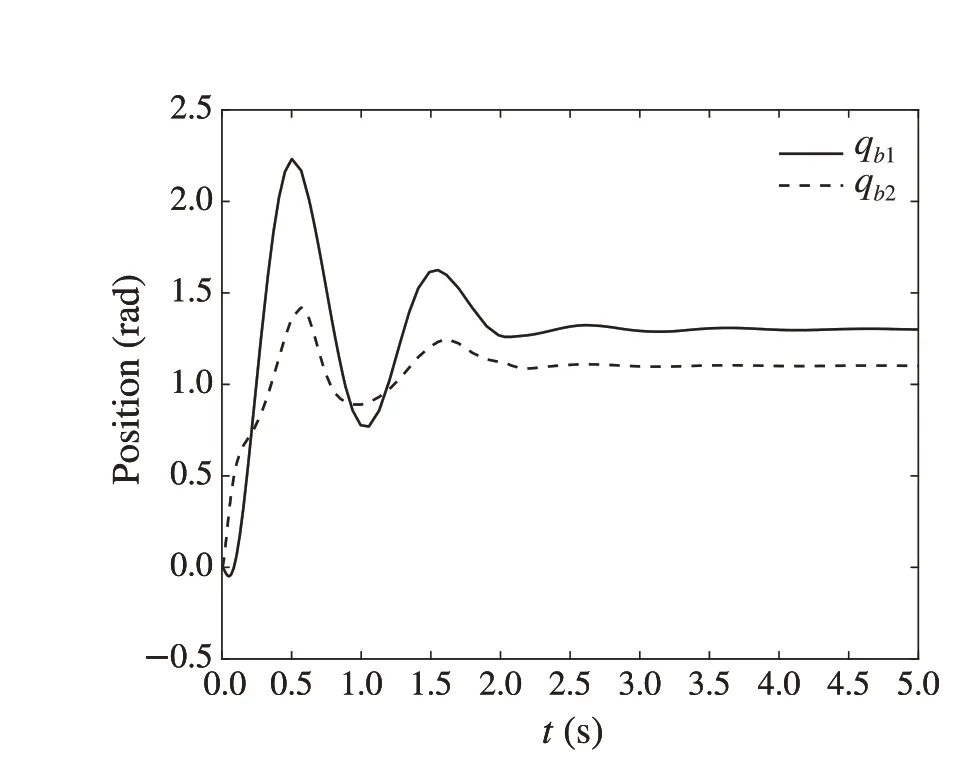
Fig.16 The angle displacement of the mechanical arm b

It can be seen from Figs. 15 and 16 that the mechanical arms a and b reach the target positions in about 4.5s.However, compared with Figs. 9 and 10, they have larger oscillation amplitudes and longer stable times.Therefore,the controller(63)can effectively reduce the oscillation amplitude and shorten the stabilization time. For example, the amplitude ofqa1in the mechanical arm a decreases from 2.007 radians to 1.317 radians,the stabilization time ofqb2in the mechanical arm b is reduced from 4.488s to 2.995s,which implies that the controller(63)designed in this paper is more effective.The specific comparison results are shown in Table 1.

5 Conclusions

In this paper, we study the robust adaptive simultaneous stabilization problem for uncertain n-degree-of-freedom multi-robot systems and design the corresponding adaptiveL2simultaneous stabilization controller. First, we present the equivalent Hamiltonian model for a robot system using the UP-DO and the potential energy shaping method, and the Hamiltonian models of the multi-robot systems are given by applying the dimensional expansion technique.And then,the adaptive simultaneous stabilization controller is designed for the multi-robot ones. On this basis, we further study the simultaneous stabilization problem of multi-robot systems with uncertain and external disturbances, and design their robust adaptive simultaneous stabilization controllers.Finally,a simulation example is given to show the effectiveness of the controller.Compared with the existing literature on multi-robot control problems (Namely, designing controllers for each system),the method presented in the paper has better control effect and robustness.

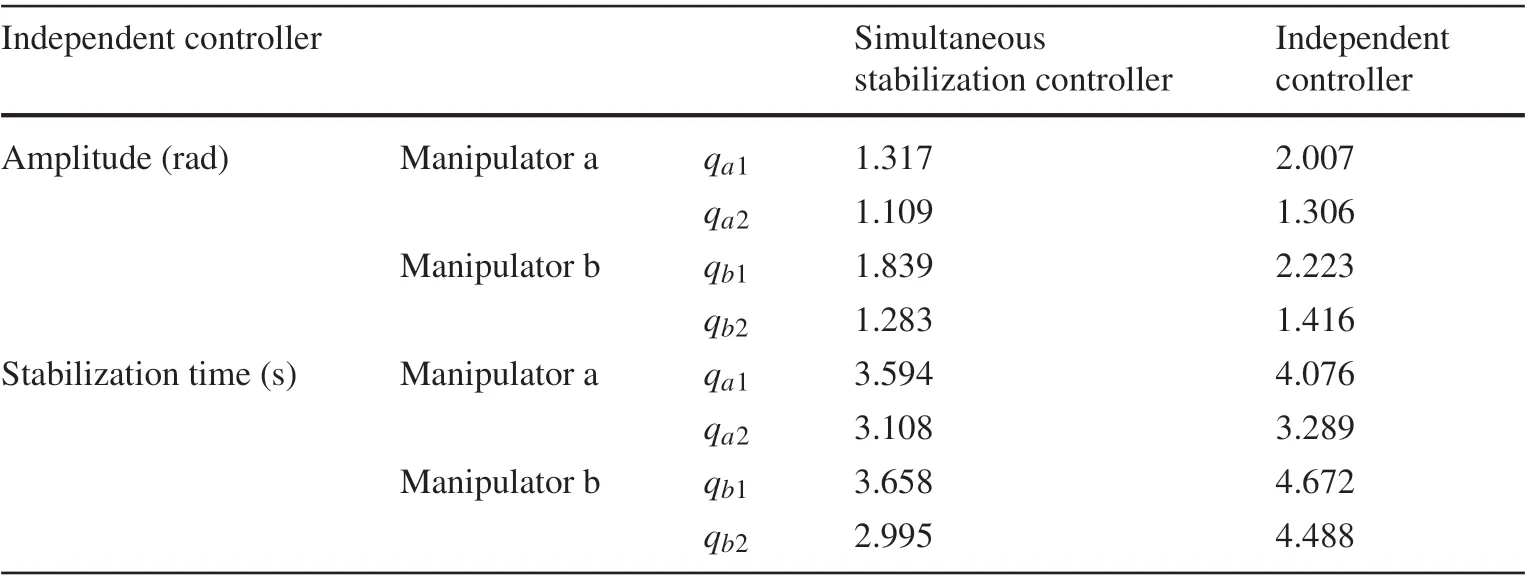
Table 1 Comparison results