Distributed robust MPC for nonholonomic robots with obstacle and collision avoidance

Li Dai·Yanye Hao·Huahui Xie·Zhongqi Sun,3·Yuanqing Xia

Abstract Considering that the inevitable disturbances and coupled constraints pose an ongoing challenge to distributed control algorithms, this paper proposes a distributed robust model predictive control (MPC) algorithm for a multi-agent system with additive external disturbances and obstacle and collision avoidance constraints. In particular, all the agents are allowed to solve optimization problems simultaneously at each time step to obtain their control inputs, and the obstacle and collision avoidance are accomplished in the context of full-dimensional controlled objects and obstacles. To achieve the collision avoidance between agents in the distributed framework, an assumed state trajectory is introduced for each agent which is transmitted to its neighbors to construct the polyhedral over-approximations of it.Then the polyhedral over-approximations of the agent and the obstacles are used to smoothly reformulate the original nonconvex obstacle and collision avoidance constraints.And a compatibility constraint is designed to restrict the deviation between the predicted and assumed trajectories.Moreover,recursive feasibility of each local MPC optimization problem with all these constraints derived and input-to-state stability of the closed-loop system can be ensured through a sufficient condition on controller parameters.Finally,simulations with four agents and two obstacles demonstrate the efficiency of the proposed algorithm.

Keywords Distributed model predictive control·Robust control·Multi-agent system·Obstacle and collision avoidance·Convex optimization

1 Introduction

The multi-agent/multi-vehicle system control problem has attracted increasing attention over the last two decades,due to their various applications in many engineering domains including the consensus problem [1,2], the flocking problem[3–5]and the cooperation problem[6,7].When dealing with multi-agent system control problems, the key aspects including global closed-loop stability, cooperative control performance, computational loads and constraints satisfaction should be paid considerable amount of attention. To this extent,the distributed model predictive control(DMPC)stands out by virtue of its inherent capacity of handling constraints,good control performance as well as relatively small computational loads compared with centralized control[8,9].Considering the ubiquitous external disturbances,distributed robust MPC has been further studied in recent years[10–12].But obstacle and collision avoidance problem is not considered in the above literature. This paper aims to explore distributed robust MPC strategy for a group of nonholonomic robots with obstacle and collision avoidance.

Obstacle and collision avoidance,which aims to avoid the collision with environmental obstacles and internal agents,respectively, have been one of the main research priorities in multi-agent system control problem due to the consideration of safety and the complexity of working environment.Recently,many state-of-the-art obstacle and collision avoidance techniques have been extensively studied, spanning from optimization-based approaches [13,14] to Lyapunovbased approaches [15,16]. The artificial potential function(APF)method,as one of the Lyapunov-based methods,has been widely used owing to its low computational requirements and ease of implementation. However, the APF method has several theoretical challenges: (i) the possible violations of physical constraints; (ii) the loss of optimality; (iii) the intractability for undesired equilibrium points.Therefore, the optimization-based approach is preferred in the considered distributed robust MPC strategy. From the practical point of view, the main challenge arises due to the fact that obstacle and collision avoidance constraints are exclusion constraints and,thus,lead to nonconvex optimizations which are known to be NP-hard in general[17].On the other hand,the formulation of obstacle and collision avoidance constraints can be divided into two cases based on the modeling of the controlled objects: point-mass models and full-dimensional objects.For sake of conceptual simplicity,a plenty of existing literature studies focus on the case of pointmass models and consider the figure of the controlled object by expanding the obstacles. However, in the actual execution process of a multi-agent control mission,the shape of the agents and the obstacles can not be ignored.Therefore,obstacle and collision avoidance in the context of full-dimensional controlled objects and obstacles is required to be explored.Related works can be seen in[18,19]and our previous work[20].

In [20], we propose a robust MPC algorithm for nonholonomic robots with moving obstacle avoidance. The moving obstacle avoidance constraints are exactly and nonconservatively converted into smooth nonconvex constraints,which result in better computational efficiency.The idea of this recent approach[20]provides silhouettes,and motivates the development of the distributed robust MPC strategy for multi-agent system control problem with both obstacle and collision avoidance in this paper.The approach in this paper builds upon several novelties:

(i) To avoid collision between agents,all the agents have to be coupled via collision avoidance constraints.In order to achieve distributed control under a synchronous update scheme, we introduce the assumed state trajectory and the compatibility constraint for each agent.The assumed state trajectories are transmitted among agents, and the upper bound of compatibility constraint is tailored to ensure the recursive feasibility of the proposed optimization problem.

(ii) This paper focuses on full-dimensional controlled objects and obstacles. To solve the challenge in computation resulted from the nonconvexity of the obstacle and collision avoidance constraints, the appropriate polyhedral over-approximations for each agent and obstacle are constructed such that the obstacle and collision avoidance constraints can be reformulated by dual optimization method.The external disturbances are taken into account explicitly in the construction of the appropriate polyhedral over-approximations. The resulting optimization problem is computationally tractable, which can be solved efficiently by standard nonlinear programming solvers.

(iii) To realize robust constraint satisfaction,a tightened state constraint set is designed.By implementing the proposed distributed robust MPC algorithm, the corresponding theoretical results such as closed-loop constraints satisfaction, recursive feasibility of each local optimization problem and input-to-state stability of the closed-loop system are ensured.

2 Problem formulation

2.1 Modeling of nonholonomic robot

Consider a multi-agent system consisting ofNanonholonomic robots indexed by subscripti∈Na:

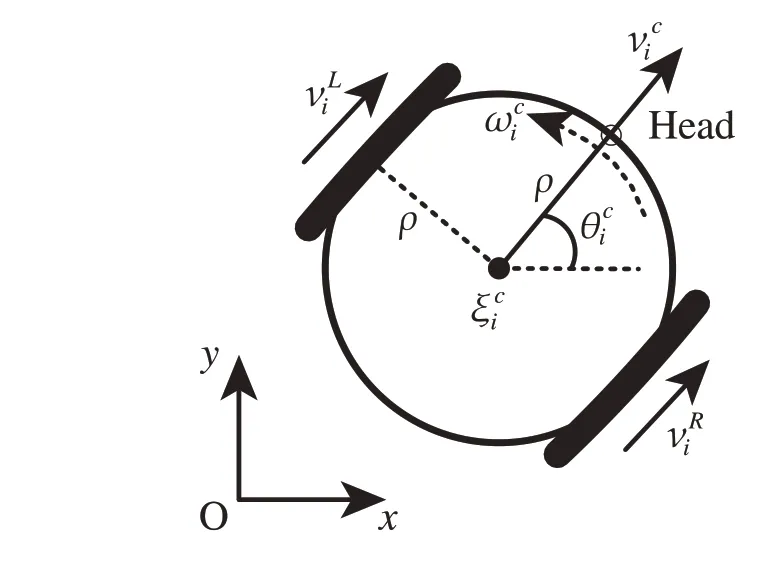
Fig.1 Nonholonomic robot structure

Each agent is able to communicate with its neighbours,and the communication network can be described by an undirected graphG=(V,E), whereV= {1,2,...,Na}denotes the set of nodes andE⊂V×Vdenotes the set of edges.The adjacency matrix is defined asA:= [ai j].If(i, j)∈E,ai j=1;otherwise,ai j=0.

2.2 Optimization formulation

The control objective of this paper is to design a distributed robust MPC scheme for the multi-agent system such that the head positionpican be regulated to its desired positionpri. Simultaneously, physical constraints and obstacle and collision avoidance constraints are satisfied during their movement. The ideal cost function of agentiat timetis defined as

It is worth noting that,the exact and direct formulation of obstacle and collision avoidance constraints Ei(k|t)∩Om=∅and Ei(k|t)∩Ej(k|t)= ∅are inherently nonconvex,which may induce heavy computation of the optimization.In order to deal with this issue, the reformulation of these nonconvex constraints will be given in Sect.3.

3 Obstacle and collision avoidance scheme

3.1 Obstacle avoidance constraint reformulation

This section will first discuss the properties of the areas Ei(k|t)and Omoccupied by the agentiand obstacles,and then the reformulations of obstacle and collision avoidance constraints will be presented.

The sets Om,m∈Mare nonempty and bounded polyhedral sets,which can be represented as

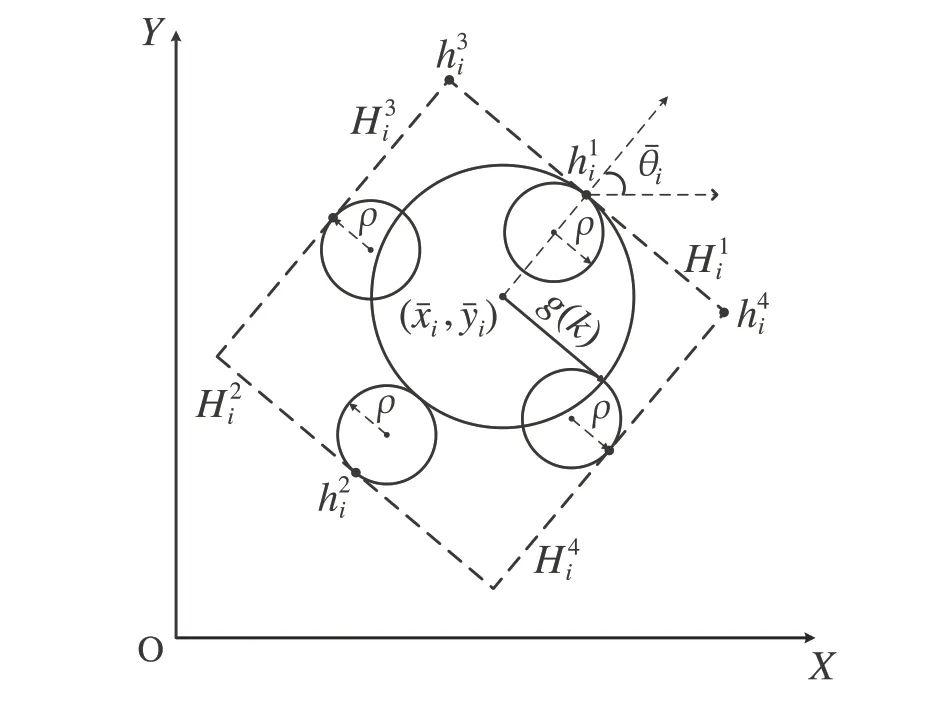
Fig.2 The sketch of the polyhedral over-approximation Di(k|t),k ∈NN-1 for the robot

This assumption guarantees the safety of the terminal constraint set such that ifpienters and no longer escapes fromΩi,there is no collision occurring.

Assumption 3 There exist sets Di(k|t),k∈NN-1, which are convex sets and satisfy

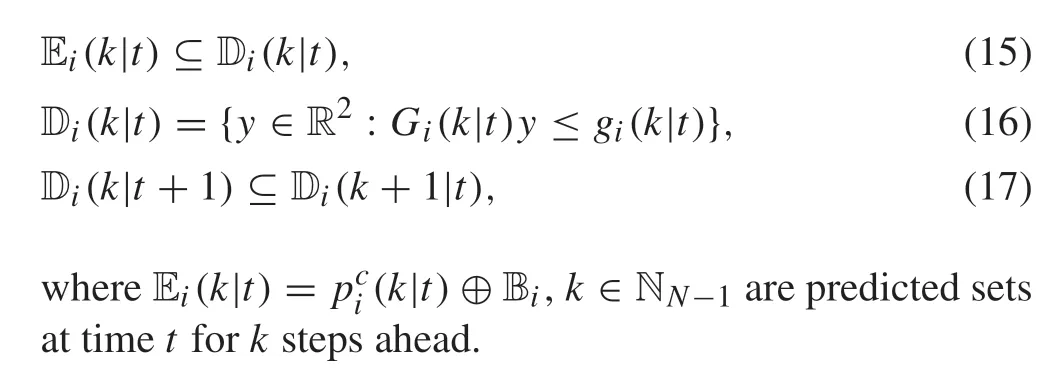
The appropriate over-approximations Di(k|t),k∈NN-1of the robot are constructed such that the robot will not escape from Di(k|t)under the external disturbances.

3.2 Collision avoidance constraint reformulation

Suppose that all agents in the system transmit information in synchronous update mechanism,in which case each agent can not get the information from its neighbours timely. To solve this problem,assumed state and input trajectories are introduced to replace the real ones.To distinguish the different predictive information,we define

The definition of assumed control input trajectory of agentiis given by

The introduction of assumed trajectories makes it possible to optimize and solve the control problem in a distributed way.However,the deviation between the assumed trajectories and the real ones may lead to great influences on the closed-loop control performance. Therefore, it is necessary to restrict the deviation by adding an extra constraint,namely compatibility constraints[14].

The compatibility constraint for agentiis expressed as

Following the construction method described in Sect. 3.1,ˆDi(k|t),k∈ NN-1is defined as a polyhedral overapproximation generated by the assumed state trajectory(22). For each agenti, taking the deviation between the predicted and assumed trajectories into consideration, the over-approximations ˆQi(k|t)to be transmitted to its neighbours are designed as

4 Distributed robust MPC algorithm

In this section,we develop a computationally tractable distributed robust MPC algorithm for multi-agent systems with obstacle and collision avoidance. The terminal ingredients including the terminal controller and terminal constraint set are also designed in this section.

4.1 Algorithm design

The main steps of the proposed algorithm are summarized in Algorithm 1.

Algorithm 1 (Distributed robust MPC for obstacle and collision avoidance)Offline stage:For each agent i,determine the parameters δ, N,dmin,γi,εi and matrices Qi and Ri required to solve Problem 2.Online stage:At the initial time t = 0,collect initial optimal control inputs ¯u*i(k|0),k ∈NN-1 and initial optimal states ¯ξ*i (k|0),k ∈NN for each agent i ∈Na.Then execute the following steps:1.At time step t,t ≥0,for agent i:a)Set the initial condition ¯ξi(0|t)=ξi(t);b) Compute the assumed control inputs ˆui(k|t), k ∈ NN-1 and assumed states ˆξi(k|t),k ∈NN using(21)and(22);c)Transmit ˆξi(k|t),k ∈NN toitsneighbouragentsandreceive ˆξ j(k|t),k ∈NN from agent j, j ∈Nai.2. Solve Problem 2 to obtain the optimal control sequence ¯u*i(k|t),k ∈NN-1.3.Apply the first element ¯u*i(0|t)to agent i.4.Update the time instant t →t +1.5.Go to step 1 and repeat this procedure.

4.2 Terminal constraint set design

The goal of this subsection is to construct the terminal constraint setΩifor agenti.To facilitate the following construction, letp1andp2be positions of agentiat any two different time instants, and we do not distinguish the variables in nominal and perturbed system in this subsection if there is no confusion.

5 Theoretical analysis

Inthissection,maintheoreticalanalysisoftheproposedalgorithm are obtained,i.e.recursive feasibility and input-to-state stability,and these will be elaborated on in detail next.

As a result of Assumption 2 and the satisfaction of(30e)att+ 1, the existence of suitableλi,m(N- 1|t+ 1),μi,m(N-1|t+1)can also be guaranteed. In particular, Proposition 1 implies thatλi,m(N- 1|t+ 1)andμi,m(N-1|t+1)satisfy (30g)–(30i) fork=N-1.Likewise,under Assumption 3,the proof of the feasibility for collision avoidance constraints (30j)–(30l) at all time steps is analogous to the above process.■

Based on Theorem 3,Lemma 2,Proposition1 and Proposition 2,the closed-loop constraint satisfaction is ensured as stated in Theorem 4.

Theorem 4 (Closed-loop constraint satisfaction)By implementing Algorithm 1, each agent satisfies state and control input constraint(4), obstacle and collision avoidance constraints(5)in the closed-loop operation at every time instant.

ProofAssume that Problem 2 is feasible at some timet.According to Lemma 2,it is easy to show that if ¯pi(k|t)∈Xki,the position constraintpi(t+k)∈Xiwill be satisfied.The control input constraint is trivially satisfied from(30d).Recalling the construction of the over-approximation set Di(k|t)in Sect.3.1 and Proposition 1,the obstacle avoidance constraint Ei(t)∩Om=∅can be ensured during the closedloop control process.By the definition of the set Qi(k|t),it is obvious that Di(k|t)⊆Qi(k|t).Therefore,Proposition 2 guarantees the satisfaction of collision avoidance constraints Ei(t)∩Ej(t)=∅.From recursive feasibility in Theorem 3,it can be concluded that constraints(4)and(5)are satisfied at all time steps.■

As stated in Theorem 5, the closed-loop stability of the global system is ensured under Algorithm 1.

Theorem 5 (Closed-loop stability)By implementing Algorithm 1,all the agents can converge to the small regions Υi,i∈Na of their desired positions.And the closed-loop system(6)is input-to-state stable.The region Υi is given by

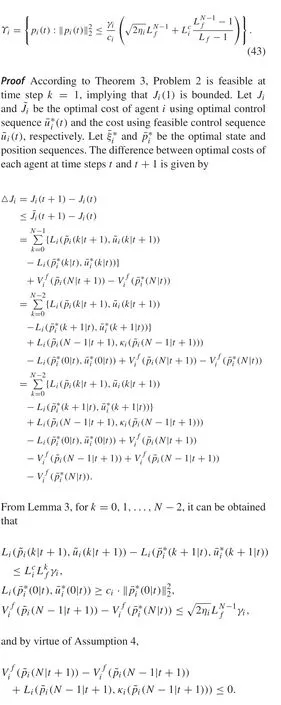
Hence,

6 Simulation results

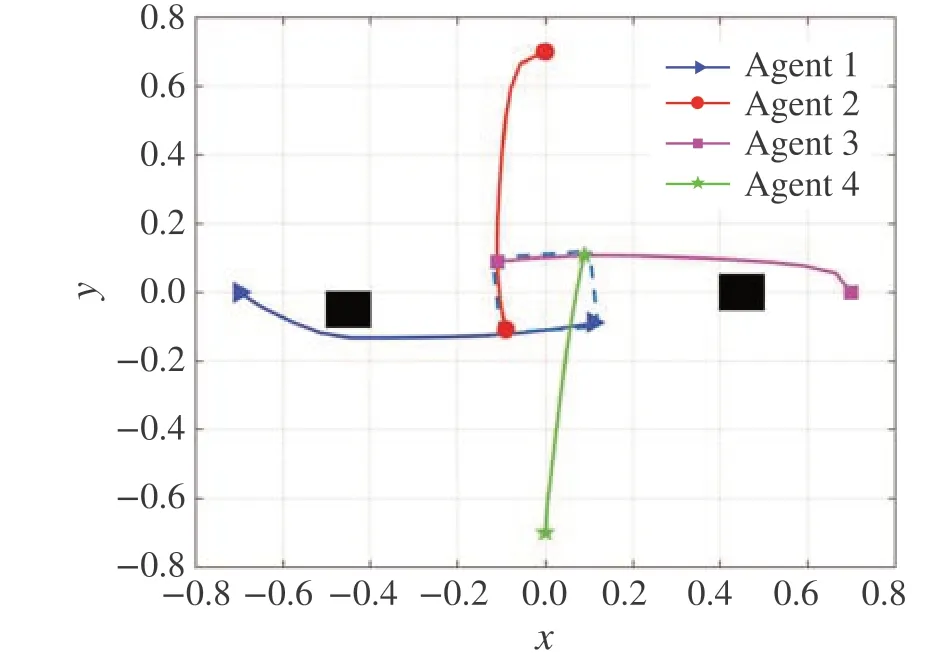
Fig.3 Trajectories of all the agents

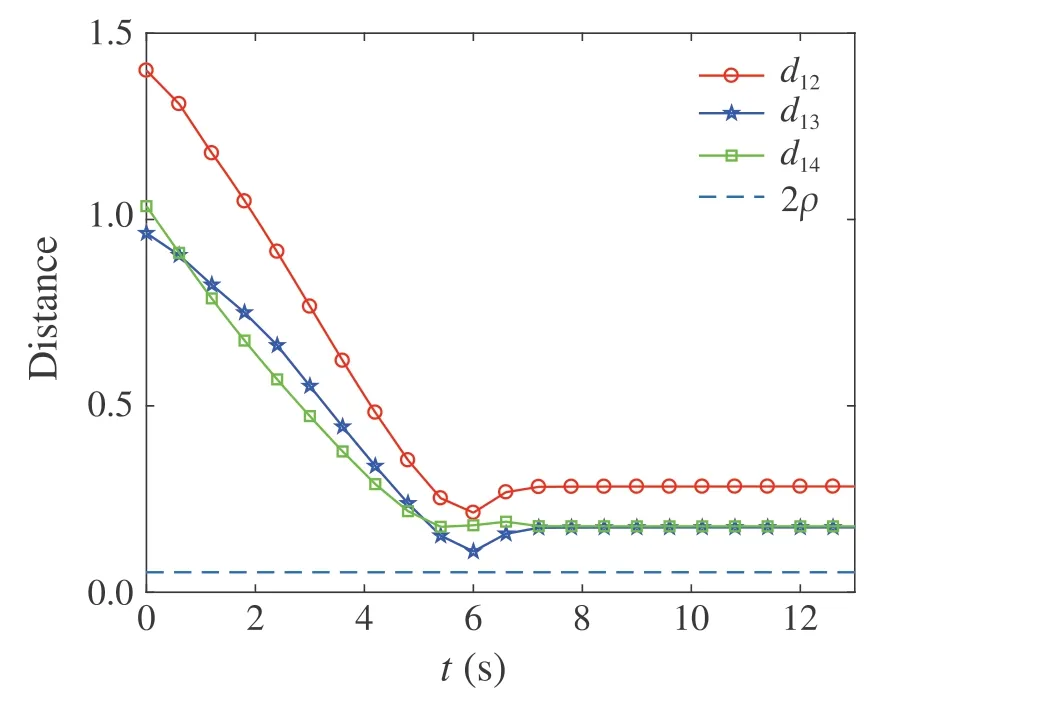
Fig. 4 The relative center distances between agent 1 and other three agents

We choose sampling timeδ= 0.6,safe distancedmin=1 × 10-4and letεi= 1.7 × 10-4,γi= 1 × 10-4. The prediction horizon isN=12.The trajectories of four agents are shown in Fig.3,in which the black rectangles represent the obstacles.Under Algorithm 1,all the agents finally enter into the small regions of their desired positions due to the existence of persistent external disturbances. This verifies the effectiveness of our approach in formation control.

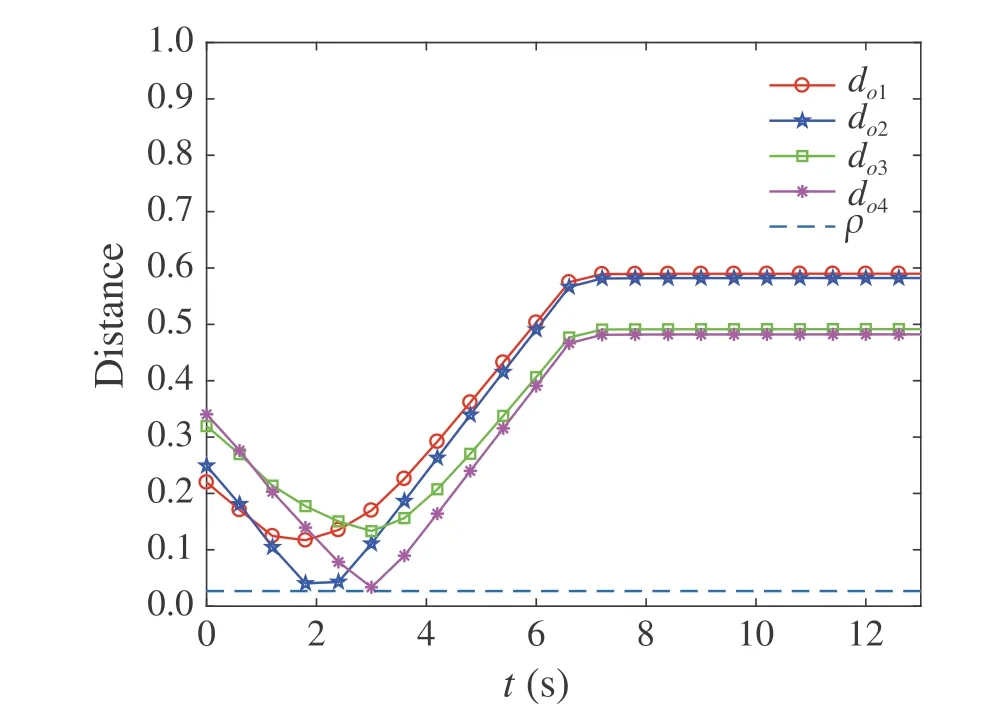
Fig.5 The relative distances between agent 1 and four vertices of obstacle O1

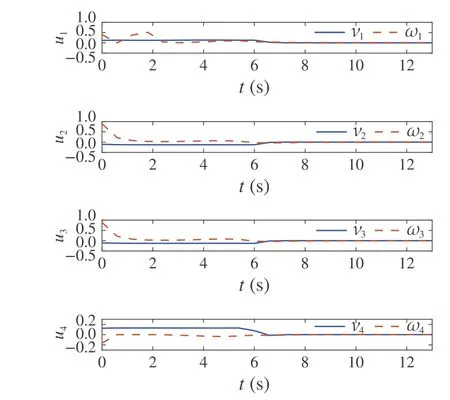
Fig.6 Control inputs of all agents

Next, we show the efficiency of the proposed approach in collision and obstacle avoidance. Taking agent 1 as an example, the collision and obstacle avoidance are clearly illustrated in Figs.4 and 5. It can be seen from Fig.4 that the relative center distances between agent 1 and other three agents are always greater than the safe distance 2ρ. This means no collision happens among the agents. Meanwhile,as shown in Fig.5,the distances between center position of agent 1 and four vertices of obstacle O1are greater than the safe distanceρ.Figure6 shows the control inputs of all agents and Fig.7 demonstrates that the inputs of all agents lie within the input constraint set Ui.It can be concluded that,for this simulation scenario,the proposed algorithm can achieve the control task effectively and safely with no collisions during the transient process.

To show the robustness of the proposed robust MPC scheme,we compare our approach with a nominal MPC strategy[14],i.e.replace the robust constraint(8b)with a nominal onepi(t)∈Xi.For this,we define the following total cost as an index By applying the two approaches to the same task as described above,we list the result in Table 1.It shows that the robust MPC spends a slightly less cost than nominal MPC(without consideration of disturbance in its optimization).

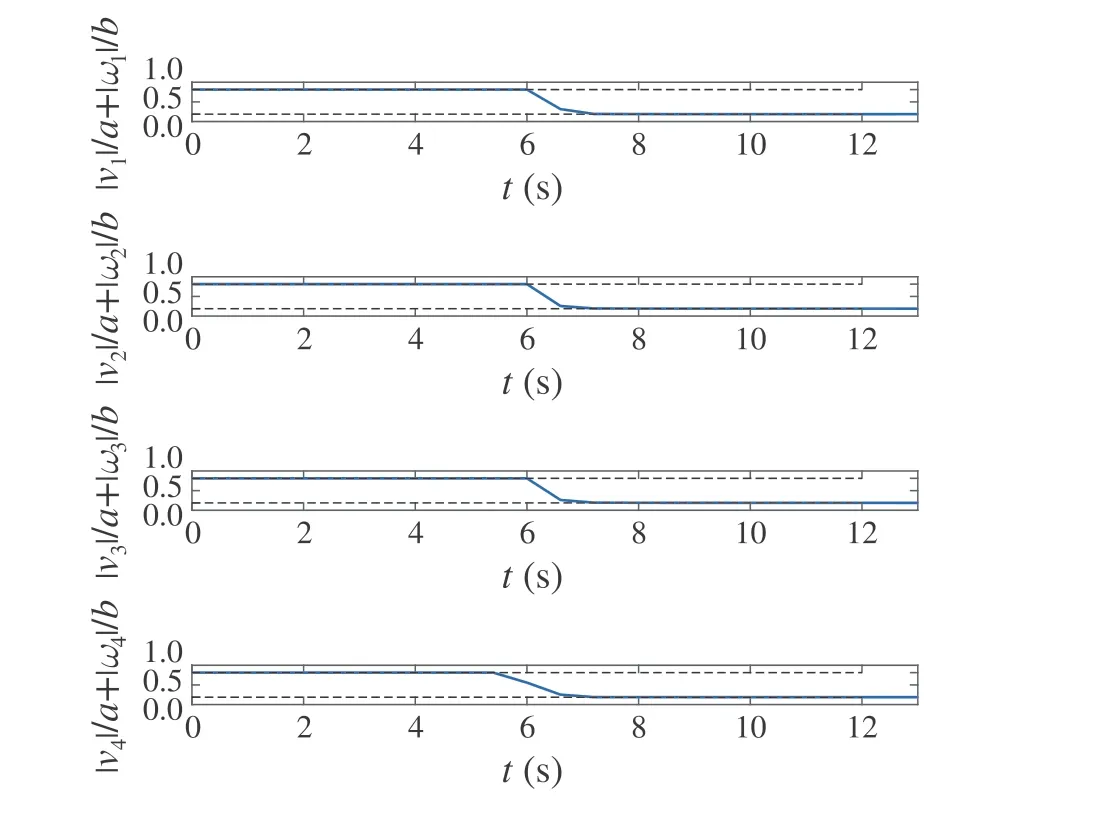
Fig.7 Input constraint satisfaction of all agents

Table 1 Comparison of global performance

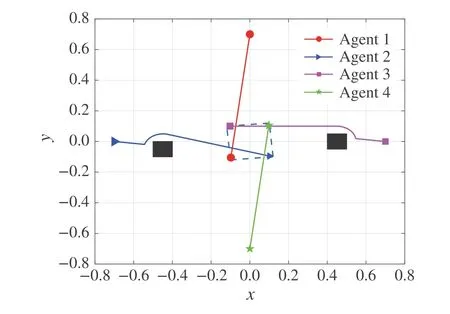
Fig.8 Trajectories of all the agents by CAPF

Moreover,wecarryoutconsensus-basedmethodwithartificial potential field (CAPF) method, see [25], for this task to show the efficiency of the proposed approach.As shown in Fig.8,the CAPF is also efficient both in formation and in obstacle and collision avoidance.However,it cannot ensure the input constraint satisfaction. This can be easily verified from the control input and its constraint index trajectories,shown in Figs.9 and 10, respectively. Additionally, CAPF takes much more cost than both the proposed robust MPC and the nominal MPC,as shown in Table 1.

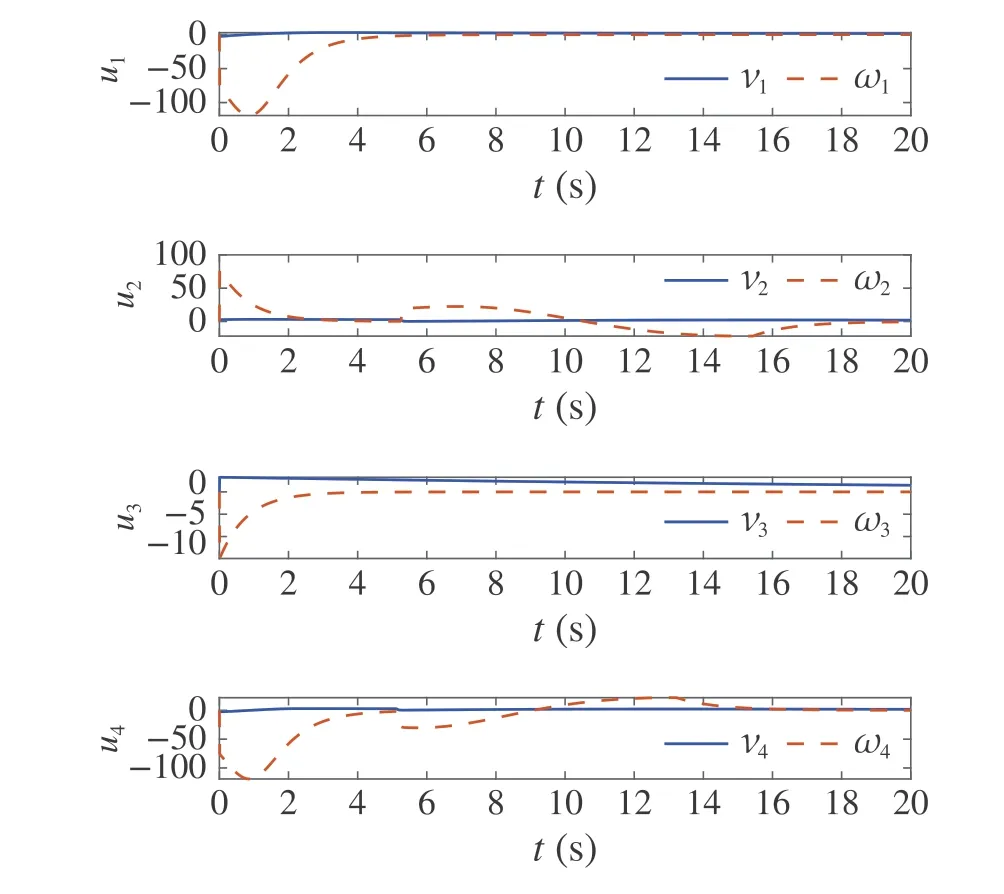
Fig.9 Control inputs of all agents by CAPF

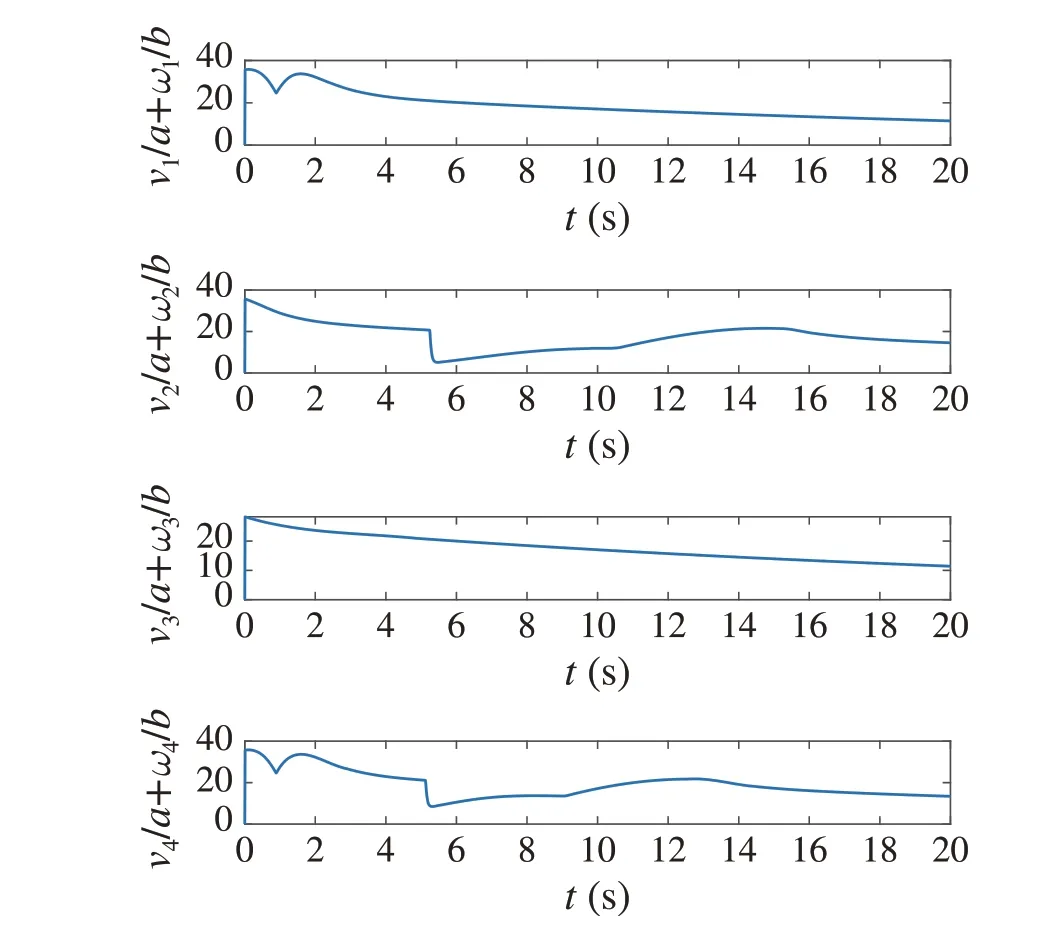
Fig.10 Input constraint satisfaction of all agents by CAPF

7 Conclusions

This paper proposes a novel distributed robust MPC algorithm for multiple disturbed nonholonomic robot systems with state and input constraints. Each agent has nonlinear dynamics and is required to avoid collisions with obstacles and other agents. This algorithm allows all agents to solvetheircontroloptimizationproblemsdistributedinasynchronous update fashion,which offers considerable benefits from a practical point of view.The distributed implementation is achieved by introducing assumed state trajectories and compatibility constraints for all agents. The tightened state constraint on nominal systems is derived to achieve robust constraint satisfaction. To tackle the nonconvexity induced by the obstacle and collision avoidance constraints,the polyhedral over-approximations of each agent and its neighbours are constructed such that the obstacle and collision avoidance constraints can be smoothly reformulated by the dual optimization method.By incorporating these constraints into the MPC optimization problem,each agent can solve a local optimization problem to obtain its own control input.A sufficient condition on controller parameters is derived to guarantee recursive feasibility and input-to-state stability of the closedloop system.