Constrained nonlinear MPC for accelerated tracking piece-wise references and its applications to thermal systems

Defeng He·Qingsong Wang·Ping Han·Haiping Du

Abstract In this paper,we propose a model predictive control(MPC)strategy for accelerated offset-free tracking piece-wise constant reference signals of nonlinear systems subject to state and control constraints.Some special contractive constraints on tracking errors and terminal constraints are embedded into the tracking nonlinear MPC formulation.Then,recursive feasibility and closed-loop convergence of the tracking MPC are guaranteed in the presence of piece-wise references and constraints by deriving some sufficient conditions.Moreover,the local optimality of the tracking MPC is achieved for unreachable output reference signals. By comparing to traditional tracking MPC, the simulation experiment of a thermal system is used to demonstrate the acceleration ability and the effectiveness of the tracking MPC scheme proposed here.

Keywords Model predictive control·Nonlinear systems·Constrained control·Tracking control·Thermal systems

1 Introduction

Model predictive control(MPC)has received more attention in the last decades due to its ability to explicitly handle constraints and nonlinearities of systems in a flexible optimal control framework [1,2]. Many results of MPC have been obtained to address the recursive feasibility, stability and robustness problems of constrained systems at some given equilibrium points[2].Most of these results are formulated as a regulation optimization problem imposed some stability terminal constraints,which aims to steer a system to a fixed operating steady-state point typically being assumed to be the origin[2–4].

The main goal of advanced control is to drive a system as close as possible to the economically optimal operating steady-state point while ensuring stability and constraint satisfaction. In practical, however, the economically optimal operating point is often altered due to,e.g.,unitary costs and changes in disturbance estimation during the operation of a process system [5–7], which leads to a piece-wise reference signal.The online calculation of stabilizing ingredients of traditional MPC is prohibitive in applications due to the inherent interplay of the ingredients [8]. Consequently, the traditional stability design of MPC with a fixed steady-state point may be invalid at a new steady-state point in the sense that the MPC controller will be fail to track the piece-wise reference signal as its recursive feasibility may be lost.Note that the offline calculation of stabilizing ingredients of traditional MPC is limited for tracking any changing piece-wise reference signal since it is available for a set of finite operating steady-state points known a prior.

Several efforts of tracking MPC have been addressed to solve the tracking problem of changing piece-wise reference signals of constrained systems. An elegant approach to address the constrained tracking problem of MPC is the so-called reference governor [9–11]. A reference governor is the nonlinear device plugged between the reference input and the pre-compensation control system. This decouples the issue of constraint satisfaction from the design of stabilization controllers,i.e.,the reference governor modifies the reference input to generate a virtual reference so as to avoid constraint violation of closed-loop systems while converging to the reference signal.

In [12], the standard dual-mode MPC was extended to track any set-point of linear systems, where an extra optimization variable was introduced to scale the terminal constraint set such that the terminal set always contains any set-point. Thereby, both recursive feasibility and stability of the tracking MPC are ensured for any set-point.In [13], a dual-mode switched MPC strategy was proposed to focus on tracking piece-wise reference signals of linear systems, where the controller switches to feasibility recovery mode and shifts the system to the feasibility region once the optimization problem loses feasibility. In [14], an integrator was plugged into the MPC feedback loop to achieve set-point tracking.In particular,this method introduced the re-initialization technique to reset the values of the integrator states at each time to improve tracking performance of the controller.In[15,16],the integrator was plugged in front of the plant directly which guaranteed the solution to the asymptotic tracking problem of MPC.In[17],the practical stability of tracking reference trajectories was established by nonlinear MPC without terminal constraints provided that a sufficiently large prediction horizon was exploited.

A promising alternative to solve the tracking problem of unreachable reference signals was presented in [18–20],where artificial steady-state points and offset cost functions were added to track any piece-wise reference signal of constrained systems.In[21],this scheme was further extended to track periodic references using artificial periodic trajectories and generalized terminal constraints [22]. The offset cost function was penalized into the tracking cost function of MPC and the artificial steady-state point was not necessarily to be closest the target reference.Although the artificial steady-state point and offset cost function increase degree of freedom of MPC optimization, it increases the computational burden of the MPC and may not always yield the preferred terminal predicted state trajectories in terms of tracking speed.

In this paper,a new nonlinear MPC scheme is presented for accelerated offset-free tracking any piece-wise reference signals of nonlinear systems subject to state and control constraints.The generalized terminal constraint[20,22]and the contractive constraints on offset cost function are used to formulate the tracking optimization problem. Then, some sufficient conditions on these ingredients are derived to guarantee the recursive feasibility and accelerated offset-free tracking ability of the MPC for changing piece-wise reference signals.Moreover,the local optimality of the tracking MPC is established in sense that the output of the closed-loop system with the tracking MPC can converge to the references being closest to the unreachable reference signal tracked.The main contribution of this work is to propose an alternative to tracking MPC design for offset-free tracking piece-wise constant reference signals of constrained nonlinear systems.This design presents a systematic method to ensure recursive feasibility and stability of the tracking MPC as well as its desired convergence speed for tracking piecewise reference signals.Namely, the stability (feasibility) of the tracking MPC and its desired convergence speed are achieved by not tuning the weighting matrices but adopting contractive constraints.The two simulation experiments of tracking temperature reference signals of a thermal system illustrate the accelerated tracking performance of the scheme proposed here.

The remainder of this paper is as follows.In Sect.2,the tracking problem is formulated. In Sect. 3, the accelerated tracking MPC scheme is presented and its theoretical properties are established.Then,an application to a thermal system is used to illustrate the effectiveness of the proposed scheme in Sect.4.Section 5 concludes the paper.

Notation Let R≥0and I≥0denote the sets of non-negative real and integer numbers, respectively. Ia:bis the set {i∈I≥0|a≤i≤b}for somea∈I≥0andb∈I≥0.A functionα: Rn→R≥0is positive definite with respect tox=sif it is continuous,α(s)= 0, andα(x) ＞0 for allx/=s. A continuous functionα: R≥0→R≥0is a class-Kfunction if it is strictly increasing andα(0)= 0,α(s) ＞0 for alls ＞0; it is a class-K∞function if it is a class-Kfunction andα(s)→∞ass→∞. For a given pair of functionsα1andα2,α1◦α2(s)denotes the functionα1(α2(s))andα1k(s)=α1◦α1k-1(s)fork∈I≥0,withα10(s)=s.The symbol“:=”denotes that the left-hand side of an equation is defined as the right-hand side.

2 Problem formulation

Consider the discrete-time nonlinear system described by

wherex∈Rnis the system state,u∈Rmis the control input,y∈Rpis the controlled output,andx+is the successor state.It is assumed that the functionsf:Rn×Rm→Rnandh:Rn×Rm→Rpare perfect and continuous on their arguments.The solution to the system for a given sequence of control inputs,u, and an initial statexis denoted asx j=φ(j;x,u)forj∈I≥0withx=φ(0;x,u).The measured state and output of the system and the control applied to the system at time stepkare denoted asxk,ykanduk,respectively.

The set of admissible equilibrium states is then defined as the projection ofZsontoX,i.e.,

Notice that setZsis non-empty sinceXandUcontain some equilibrium points in their interior andXsis also nonempty.

When tracking a piece-wise reference signalr,the system shall not converge to the origin but settle at the steady-state point(xr,ur)at which it holds thath(xr,ur)=r. A reasonable selection of such steady-state point is to minimize energy input,which can be formulated as

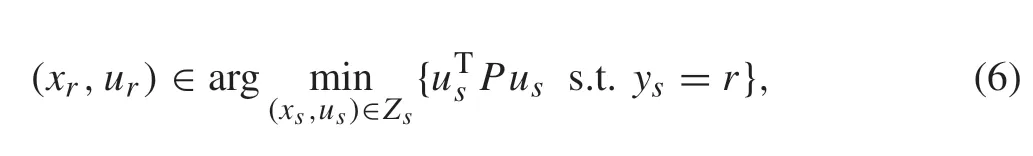
where the weighted matrixP= diag{p1,p2,...,pm}, is a positive-definite one, i.e.,pi ＞0 fori= 1,...,m. For simplicity,we assume that(xr,ur)is unique for the reference signalr; otherwise, let(xr,ur)be any of the steady-state points satisfying(6).

The goal of this work is to design an offset-free tracking MPC lawμ(x;r)of constrained nonlinear system (1)such that the closed-loop system settles the steady-state point(xr,ur)withh(xr,ur)=rfor any(possible time-varying)piece-wise reference signalrto be followed,while fulfilling the constraints in(2).

The changes of the reference signals to be followed will alter the target steady-state point, to which the system (1)has to converge.Hence,the challenge of the tracking MPC is to ensure its recursive feasibility and convergence to any changing piece-wise reference signals in the presence of the state and control constraints.

3 Design of tracking MPC controllers

Consider the system (1) with a piece-wise reference signalrat time stepk.LetE(x,u;r):=E(x-xr,u-ur)be a positive definite function with respect to(xr,ur)associated withr, i.e.,E(x,u;r)≥0 for any(x,u)∈X×UandE(x,u;r)= 0 if and only if(x,u)=(xr,ur). Moreover,set ˆJk≥0 and ˆEk≥0 are two scalars at time stepk,which will be specified later on.

LetN∈I≥0be a finite number andx∈Xbe the state at time stepk.For the system(1),we define the cost function as

Remark 1Note that the conditions (8f) and (8g) can be viewed a set of “hard” constraints imposed to guarantee convergence of the tracking MPC. This will accelerate the controller to track the changing piece-wise reference signals comparing to the traditional weighted tracking MPC that penalizes the terminal steady state errors with respect to the target steady state associated with the reference.Note that if the reference is fixed a prior,then in principle it is possible to achieve a desired convergence speed by elaborately tuning the weights in traditional MPC with trial and error.However,the changing reference may yield loss of recursive feasibility and stability of the traditional MPC due to the changing steady-state point associated with the reference.On contrary,in this work,we presented a systematic method of adopting contractive constraints to ensure recursive feasibility and stability of MPC as well as its desired convergence speed for tracking piece-wise reference signals.Note that in this work,stability(feasibility)of the tracking MPC and its desired convergence speed are achieved by not tuning the weighted matrices but adopting contractive constraints.

Algorithm 1(Accelerated tracking NMPC algorithm)

Step1(Initialization):PickN ＞0,σ∈(0,1)and a sufficiently largeξ ＞0.Set(˜E,˜J)→+∞and letk=t=0.For a givenxk∈X,set ˆEk(rt)= ˜Eand ˆJk(rt)= ˜J.Solve the optimization problem (8) withx=xkand obtain its optimal solutionu*(xk;rt). Implement the control actionuk=u*0(xk;rt)to the system(1)and letk=1.

Step2:Measure the statexkat the time stepk.

Step3:Measure the reference signal to be tracked.

If the reference signal is different to the one at the time stepk-1, then update the cost function (7) with the new target steady-state point obtained by solving (6); letk=tand set ˆEk(rt)= ˜Eand ˆJk(rt)= ˜J.

Else,evaluate ˆEk(r)and ˆJk(r)by(9)–(11)withr=rt.

Step4: Solve the optimization problem (8) to obtain its optimal solutionu*(xk;rt).

Step5: Apply the control actionuk=u*0(xk;rt)to the system(1).

Step6:Letk=k+1 and go back to Step2.

From Algorithm 1 and the receding horizon principle,the tracking MPC lawμ(x,ˆE,r)is defined as the first action of the optimal solution to(8),u*(x;r),i.e.,

which gives rise to the following closed-loop system:

wherex j=φ(j;x,u).The setχN(x)contains all the possible steady states that can be reached in at mostNsteps with an admissible control sequenceu, starting fromx. Clearly,it is obtained thatN1＜N2⇒χN1(x)⊆χN2(x).

For a givenx∈X N, we define an achievable minimal value ofE(x,u;r)as

Remark 2Note that in practical,the value ofE*(x;r)needs not to be known explicitly in the initialization step of Algorithm 1. In fact, selecting any value of such that the optimization problem(8)is initially feasible,i.e., ˜E∈S.

Remark 3It is known that the optimal terminal state-input pair(x*N,u*N)is generally different from the target steadystate point(xr,ur)and indeed it is varying at each time step.To this end, the tracking MPC obtained by Algorithm 1 is computed as the output of the resulting closed-loop system(18)with internal state ˆEand inputx.Hence,the controller(12)can be seen as one of the dynamical feedback tracking controllers, which is different from the typical static feedback tracking MPC controllers (see, e.g., [2] and reference therein). Moreover, the contractive constraint (8f) ensures that the internal state ˆEis rigidly decreasing and can be guaranteed to converge to zero under some assumptions.

Assumption 1 There exist class-K∞functionsα fandαlsuch that‖f(x,u)-f(z,v)‖ ≤α f(‖(x,u)-(z,v)‖)and‖E(x,u;r)-E(z,v;r)‖ ≤αl(‖(x,u)-(z,v)‖)for any(x,u),(z,v)∈X×Uand some vector norm‖·‖.

Assumption 1 implies that the changes of functionsfandEwith respect to any two-point being inX×Ucan be limited by the class-K∞functionsα fandαl,respectively.This assumption can be viewed as the generation of the Lipschitz condition of functions. Note that sincef(x,u)is continuous on its arguments andE(x,u;r)is positive definite with respect to(xr,ur),these class-K∞functions exist in the finite dimensional case withXandU.

Assumption 2 The set of reachable terminal states,χN(x),contains the target steady-state point(xr,ur)as its interior.

Assumption 2 provides an variant of the controllability condition [2] of system (1) with respect to the point(xr,ur).Namely,there exists an admissible control sequenceu(x)such that the closed-loop trajectory reaches the target point(xr,ur)withinNsteps, starting fromx. Namely,E*(x;r)= 0. Nevertheless, the sequenceu(x)is not necessarily an optimal solution to the optimization problem(8).Let

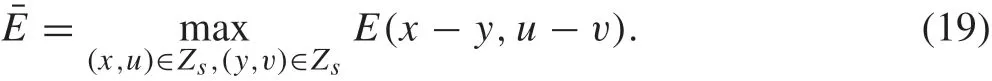
Due to the compact setsXandUand the continuity of the functionsf(x,u)andE(x,u;r),the maximum(19)exists.

Our first result is concerned with the recursive feasibility property of the optimization problem(8)in Algorithm 1 under a changing reference signal.Recall that recursive feasibility of MPC can usually be proven with the usual argument of constructing a feasible solution at timekwith the tail of the optimal solution computed at timek-1,padded withu*N|k-1as the last control input[2].However,this usual argument is not available for the problem (8) even for a fixed reference signal since such constructed sequence as(9)does not satisfy the constraint(8f).To address this problem,we first establish sufficient conditions onξunder which recursive feasibility of(8)holds for any changing reference signal to be tracked.

Theorem 1Under Assumptions 1 and 2, the optimization problem (8) is recursively feasible within the invariant set X N for a sufficiently large ξ ＞0and an˜E≥¯E.ProofFirst, we consider the time steptat which the reference signalrchanges. According to Algorithm 1, we have ˆEk(rt)= ˜Eand ˆJk(rt)= ˜J. Notice that the constraints(8b)–(8e) are independent of the target steady-state point(xr,ur).Moreover,the selection of ˜E≥ ¯Eimplies that the setχN(xt;rt)contains the target steady statexrt,associated with the reference signalrt,as its interior.Hence,there exists a feasible control sequence ˜u(xt)to satisfy the constraints(8b)–(8g).

Second, we consider the other time steps at which the reference signalrhas no change.In this case,from Assumption 2 one can pick a sequence ¯uconsisting ofNcontrol inputs such that constrains (8b)–(8e) are satisfied andE(¯xN,¯uN;r)=E*(¯xN;r)= 0. It is clear that the constraint(8f)is satisfied due to ˆEk(r)≥0 for any signalr.

To derive the constraint(8g),we consider the value of the cost function associated with the sequence ¯u

holds. Note that due to the compactness ofU, the value ofηis finite.Hence,the constraint(8g)holds for a sufficiently largeξ ＞0 and correspondingly,the sequence ¯uis a feasible solution to(8).This implies that the recursive feasibility of the optimization problem(8)is established.■

Next, we present the convergence to the piece-wise reference signals of the system(1)in the closed loop with the tracking MPC controller(12).

Theorem 2Suppose that Assumptions 1 and 2 hold and the problem(8)isinitiallyfeasibleatinitialtimestepk=0.Then for a sufficiently large ξ ＞0and an˜E≥ ¯E,the output of the closed-loop system(18)converges to the reference signal r(t)within the invariant set X N.

ProofFrom Theorem 1, the problem (8) is feasible at any time step under the assumption of initial feasibility. Letu*(x;r)be the optimal solution to(8)at time stepk.Substitutingu*(x;r)into the cost function(7),we define the value function as

Remark 4Notice that the convergence of the closed-loop system is uniform with respect to the changing (possibly time-varying)piece-wise reference signalr.Since the set of admissible initial statesX Ndoes not depend on(xr,ur)orr,the proposed controller is able to guarantee recursive feasibility and constraint satisfaction for anyrk,k ＞0. Moreover,ifrkconverges to a constant value, the controller ensures closed-loop convergence to(xr,ur).In fact,since the domain of attractionX Ndoes not depend on the optimal steady-state point,for allxk∈X Nevery admissible steady state is reachable. Moreover, if the reference changes, the problem (8)does not lose feasibility since the trajectory remains inX Nand the system will be driven to the new target steady-state point in an admissible way.

Remark 5From the proof of Theorem 2, it is known that the convergence behavior of the closed-loop trajectories with our MPC is dominated by the adopted contractive constraints(8h)and(8g).Of course,due to the constraints of system(1),it is a prior guaranteed that the MPC optimization problem(8)has to be recursively feasible.Hence,the parameterξin our method is used to guarantee the recursive feasibility of(8),whichcanbeobservedfromtheproofofTheorem1.Notethat the condition of the sufficient largeξis merely sufficient for Theorem 1.In this sense,one can pick a sufficient large value ofξsuch that the problem(8)is initially feasible regardless of the convergence speed.This is do one of main advantages of our method compared with the traditional tracking MPC.In addition,it is known from Algorithm 1 that ˜Eis used at the time when starting or the reference signal changes. In fact,at those times,the constraints(8f)–(8g)will be not activated,which can be formulated by the condition of ˜E≥ ¯E. Of course,this condition is only sufficient for Theorems 1 and 2,too.

Corollary 1Consider the constrained system(1)–(2)and the set of reachable terminal states χN(x) with no containing the target steady-state point (xr,ur) as its interior. Under Assumption 1, the tracking MPC controller (12) is locally optimal in such sense that it can drive the state trajectories to the state in χN(x)being closest to the target steady state xr.

ProofThe proof is directly followed from [20] and then is omitted for saving spaces.■

4 Application to a thermal system

In this section, a multi-input and multi-output nonlinear thermal system is used to evaluate the performance of the proposed tracking MPC scheme.The schematic of the thermal system is shown in Fig.1,which was firstly introduced in[25]to verify the effectiveness of the stabilizing MPC with switching regulation objectives.Here the proposed tracking MPC is adopted to drive the thermal system to track a changing piece-wise temperature reference signal.

The system in Fig.1 is composed of a metal box embedded in a plate.The main goal is to regulate the temperature of the internal metal box(Tb)and the plate(Tp)to reach the desired operating temperature as fast as possible.This is operated by three heaters,i.e.,the available control inputs are the powerWp1andWp2provided by the two heaters of the plate and the powerWbof the heater that heats the metal box directly.Furthermore,the external temperature inherently disturbs the thermal system by causing a radiative cooling of the plant.In practical,the thermal system is regarded as a district heating system.Namely,the controller is designed to control the temperature of the plate and metal box with temperature differences byheat exchangingviaconvectionbetweentheplant and the box itself.

The dynamics of the thermal system can be given by[25]

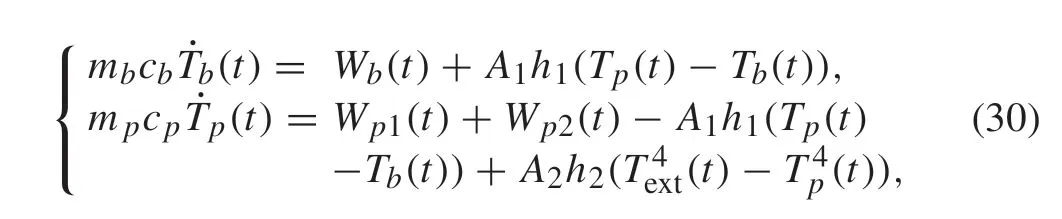
whereTextistheexternaltemperature,withthegivenconstant value 263K.The model parameters of(30)are introduced in[25]:mb(3kg)andm p(20kg)are the box and plate masses,cb(4300 J/(kg·K))andcp(4000 J/(kg·K))are the box and plate specific heats,h1(200kg/(K·s3))is the box convection coefficient,h2(9.203×10-7kg/(K·s3)) is the plate radiative coefficient,A1(0.3m2) andA2(0.8m2) are the areas of the box and plate. In this study, the temperature of the internal metal box(Tb)and the plate(Tp)are selected as the state variablesx1andx2,respectively,and the heatersWp1,Wp2andWbare selected as the control inputsu1,u2andu3,respectively. The thermal system(30) has to satisfy the following constraints at each time:

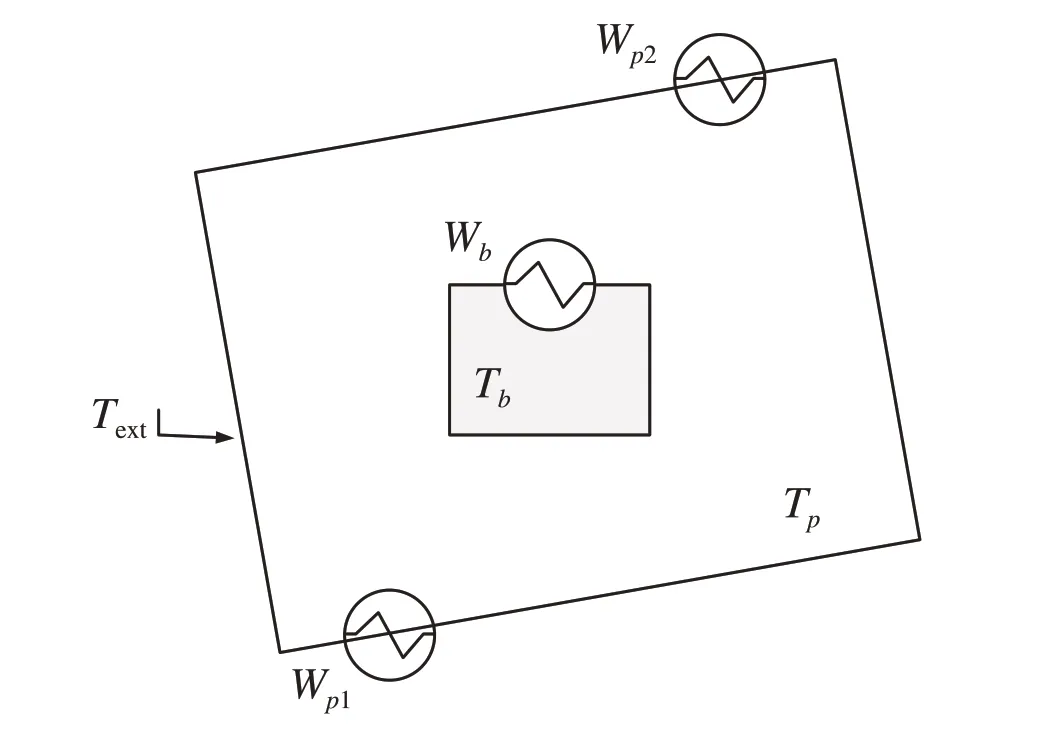
Fig.1 A schematic of the considered thermal system

The discrete-time model of system (30) is obtained by the Eulerian difference method with the sampling time interval 5 s. LetN= 10 andE(x,u;r)=(x-xr)TQ(x-xr)+(u-ur)TR(u-ur)withQ= diag{0.1,0.1} andR=diag{1,1,1}.Two experiments are exploited to demonstrate the proposed tracking MPC scheme (denoted by Our-TMPC).The first experiment is to verify the effectiveness of Our-TMPC.The second experiment is to assess the performance of Our-TMPC by comparing to the tracking MPC scheme with penalizing the terminal steady state errors[20] (denoted by W-TMPC). All optimization problems in these schemes are solved by the function fmincon in MatLab 2013a environment on the laptop with an i7-5500U central processing unit with 2.4GHz and 4GB random access memory with Windows 10.

4.1 Performance verification of Our-TMPC

To illustrate the proposed tracking MPC controller, let the output variable of system (30) bey= [x1,x2]T. Then, the control goal of this experiment is to steer the output of(30)to offset-freetrackachangingtemperaturepiece-wisereference signal.

Let the simulation time steps be 300 sampling intervals and the temperature piece-wise reference signal be set as

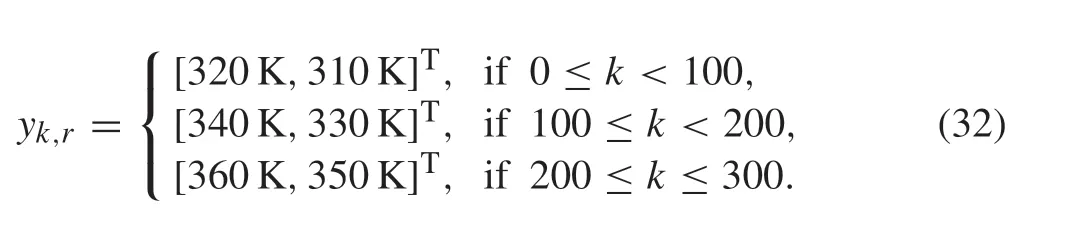
Moreover, the matrixPin (6) is selected as diag{0.3,0.4,0.3}. Then, the optimal steady-state points associated with the reference signals(32)are calculated as

In this paper,pickx0=(350 K,320 K)as an initial state of system(30)and the parameter of the controller asσ=0.7.Figs. 2 and 3 separately show the time evolutions of the closed-loop states and the control inputs obtained by applying Algorithm 1 for different values of parameterξ.In Fig.2,the solid lines(ξ= 0.1),dashed lines(ξ= 100)and dashdotted lines(ξ=7000)are the closed-loop state trajectories of system(30)in closed with Our-TMPC and the dotted lines are the changing reference signal.It can be seen from Fig.2 that the closed-loop state trajectories rapidly converge to the changing target steady states (33) and the controlled outputsycan quickly track the changing temperature piece-wise reference signal (32) with no offsets for different values of parameterξ.It is worth noting that from Figs.2 and 3,one can see that the convergence behaviors of the closed-loop system are almost the same for different values ofξin the cost function(7).Namely,there is little impact of parameterξon the convergence performance of the closed-loop system.Moreover, it is observed from Figs. 2 and 3 that the system constraints in(31)are always fulfilled at each time step regardless of the changing temperature reference signal(32).These verify that the proposed tracking MPC is ensured to be recursively feasible for any changing piece-wise reference signal and has an ability to offset-free tracking the changing piece-wise reference signal in the presence of constraints on the state and control.

Moreover, a target temperature referenceyr= [420 K,410 K]Tis picked to illustrate the local optimality of the proposed tracking MPC. Clearly, this reference is unreachable as it does not satisfy the constraints (31). Figure 4 pictures the time evolutions of the closed-loop states driven by applying Algorithm 1, where the solid lines are the closed-loop state trajectories of(30)with Our-TMPC and the dash-dotted lines are the unreachable reference signal.From Fig.4,it is clearly observed that Our-TMPC can drive the thermal system(30)to converge to the reference for the reachable target temperature reference while tracking the closest admissible steady-state pointx=(400 K,400 K)for the unreachable target temperature reference.

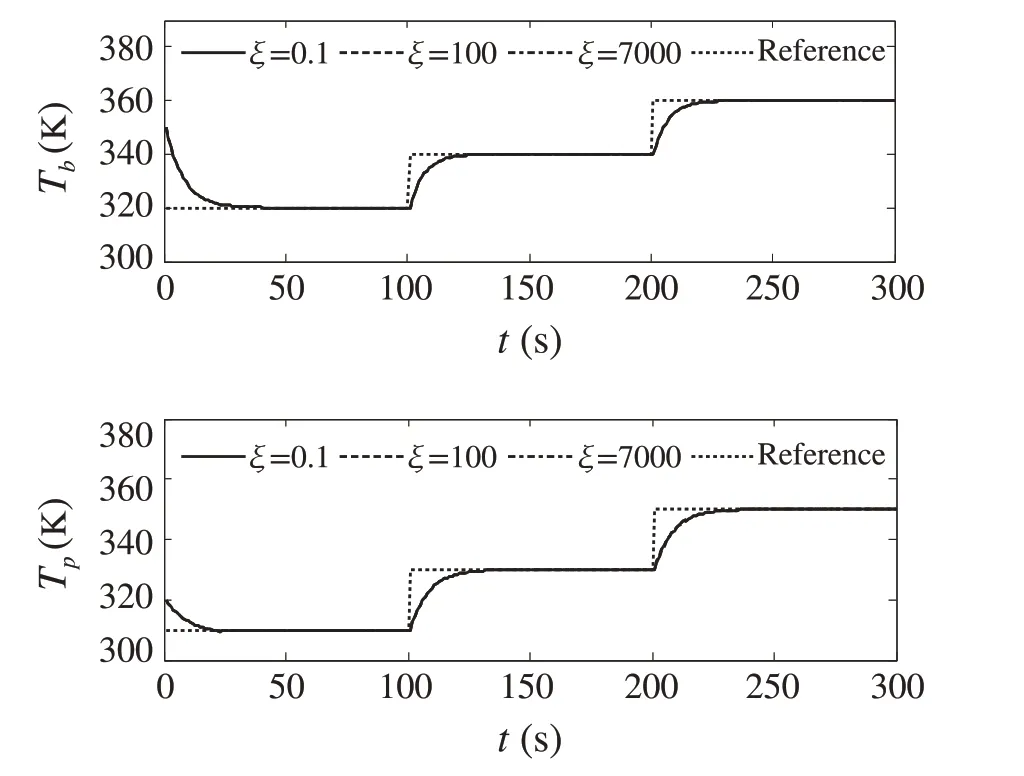
Fig.2 Temperature reference signal and time evolutions of box temperature Tb and plate temperature Tp for different ξ

Fig.3 Control input profiles of Wp1,Wp2 and Wb for different ξ

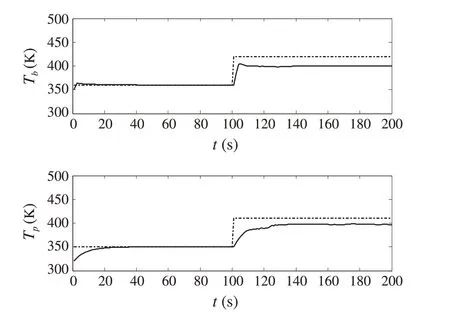
Fig.4 Temperature reference signal(dash-dotted lines)and time evolutions(solid lines)of box temperature Tb and plate temperature Tp

4.2 Performance comparison of controllers

In this section,we assessed the performances of two tracking MPCcontrollers,Our-TMPCandW-TMPC.Tothisend,pick the temperature piece-wise reference signal

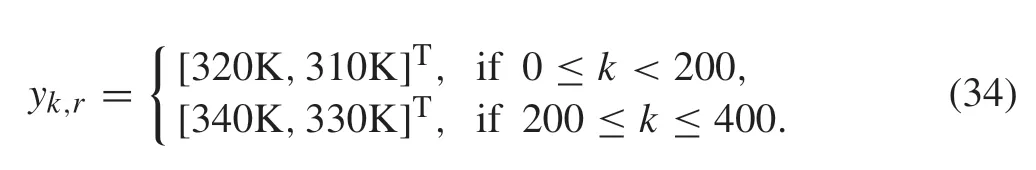
That is,the temperature reference will be switched at the time step 200.

Figure 5 shows the time evaluations of stage cost functionE(x,u;r)at admissible terminal steady-state points,where dashed line is obtained by employing Our-TMPC and solid line is obtained by employing W-TMPC.Note that in both tracking MPC schemes,E(x,u;r)will not be directly equal to zero since admissible terminal steady-state points are not generally identical to the target steady-state points when solving the problem(8)at each time.Moreover,it can be seen that in W-TMPC, the time evaluations of the stage cost function (solid line) are not monotonic when tracking the constant references whilst,they(dashed line)are monotonically decreasing in Our-TMPC.This is the reason that the contractive constraints in(8)rigidly restrict the choice of the admissible steady-state points to be the equilibrium points being closest to the target whilst in W-TMPC,the weighted offset terminal stage cost function of a target steady state cannot rigidly limit such choice of the admissible steadystate points.This difference of both tracking MPC schemes in choice of the admissible steady-state points leads to the different speeds of convergence to the target references.

Figures 6 and 7 show the time evolutions of the closedloop states and control inputs obtained by separately implementing the two MPC controllers in the same simulation context.The solid and dotted lines represent the corresponding results of Our-TMPC and W-TMPC, respectively, and the dash-dotted lines represent the temperature piece-wise reference signal (34). From Figs. 6 and 7, one can see that the output controlled by both tracking MPC are asymptotically converge to the reference signal in the presence of the state and control constraints and the changing temperature reference signal.However,the output trajectories of the closed-loop system (30) with both tracking MPC approach the target reference in different ways.

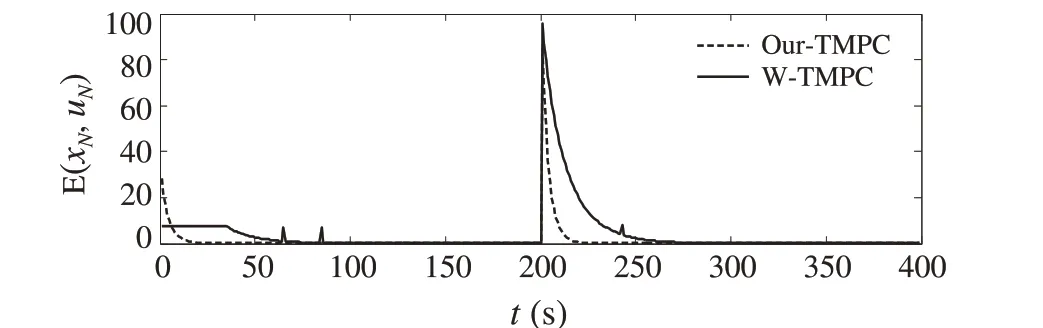
Fig.5 Time profile of stage cost function w.r.t terminal states and inputs for Our-TMPC(dashed line)and W-TMPC(solid line)

Fig.6 Time evaluations of box temperature Tb and plate temperature Tp for Our-TMPC (solid lines) and W-TMPC (dashed lines) and the reference temperature signal(dash-dotted lines)

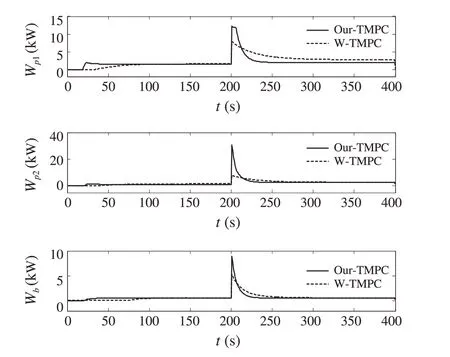
Fig.7 Control input profiles of Wp1,Wp2 and Wb for Our-TMPC(solid lines)and W-TMPC(dashed lines)

In particular, it is obviously observed that the transition time of the closed-loop system (30) with W-TMPC is longer than that of the closed-loop system (30) with Our-TMPC when the temperature reference switches. Namely,Our-TMPC takes 34 time steps to converge to the reference signal, while W-TMPC takes an average of 106 time steps to converge to the reference signal. This implies that Our-TMPC has an accelerated offset-free tracking performance with respect to W-TMPC.This difference of transition times can be explained by the different operations on the offset terminal stage cost function (see Fig. 5). Note that the accelerated tracking performance of a controller is important to ensure the safe operation of systems in some special conditions[7,26].On the other hand,one can see from Fig.7 thatatthetimewhenthereferencesignalswitches,thepeakof the control actions obtained by Our-TMPC is larger than that by W-TMPC.The increasing control inputs at the switching times contribute to accelerate the convergence to the reference after the reference signal switches.It should be pointed out that the peak of the control actions obtained by Our-TMPC still satisfies the control constraint (31) although it may cause a dissatisfactory action of actuators in practical applications.Relaxation of the peak of control actions is one of the studies pursued in the future.

5 Conclusions

In this paper,we proposed a new accelerated tracking MPC scheme for offset-free tracking piece-wise constant reference signals of constrained nonlinear systems. The generalized terminal constraint was used to ensure re-cursive feasibility of the tracking MPC for any changing piece-wise reference signals. Some sufficient conditions on contractive terminal functions and cost functions were derived to establish asymptotic convergence to the piece-wise reference signal.Moreover, the proposed tracking MPC was guaranteed to have the local optimality if the reference signal is unreachable. The effectiveness and superiority of the proposed tracking MPC were illustrated by two simulation experiments of tracking a changing temperature reference signal of a complex thermal system.