Adaptive output regulation for cyber-physical systems under time-delay attacks

Dan Jin·Bo Chen·Li Yu·Shichao Liu

Abstract In this paper,we present an output regulation method for unknown cyber-physical systems(CPSs)under time-delay attacks in both the sensor-to-controller(S-C)channel and the controller-to-actuator(C-A)channel.The proposed approach is designed using control inputs and tracking errors which are accessible data.Reinforcement learning is leveraged to update the control gains in real time using policy or value iterations.A thorough stability analysis is conducted and it is found that the proposed controller can sustain the convergence and asymptotic stability even when two channels are attacked. Finally, comparison results with a simulated CPS verify the effectiveness of the proposed output regulation method.

Keywords Adaptive output regulation·Cyber-physical systems·Time-delay attacks·Reinforcement learning

1 Introduction

Cyber-physical systems(CPSs)integrate computation,communication and control to achieve the desired performance of physical processes[1].CPSs have been implemented in a wide range of applications such as industrial manufactures[2],smart grids[3],transportation networks[4],health and medicine[5].However,the integration of computation,communication and control in turn makes CPSs vulnerable to cyber attacks[6].In recent years,the number of CPS security incidents has increased rapidly[7],and some incidents have caused critical damages to the infrastructures such as Stuxnet in Iraq[8]and BlackEnergy in Ukraine.Therefore,it is vital to innovate the security of CPSs.

Many security problems come from cyber attacks.Timedelay attacks [9–11], as one kind of cyber attacks, tamper with temporal characteristics of the communication channels and lead to signal delays in certain network nodes[12].Being different from DoS attacks, time-delay attacks are less costly and harder to be detected [13–15], due to the fact that time-delay attackers only need to occupy part of the channel without blocking the whole transmission. At the same time, time-delay attacks are easier to be implemented technically than deception attacks[16–18],as there is no need for time-delay attackers to capture and tamper the information. Furthermore, though time-delay attacks cause the transmitted information to be delayed, it is different fromnetwork-induceddelays.Thisisbecauseattack-induced delays are destructive and the instantaneous fluctuations of delays can be very large.If attack-induced delays cannot be handled well, they may affect the normal operation of the system seriously,especially for the CPSs with high real-time requirements. Therefore, it is crucial to address the timedelay attacks in CPSs.

In the existing works,several approaches have been proposed to deal with delays in CPSs, including the random method[19,20],the robust method[21,22],and the switched system method[23,24].Though delays can be handled well with these methods, most of the works require the exact knowledge of the system model.Recently,model-free methods have been increasingly designed in the field of control[25–32]. Reinforcement learning (RL) [33], which learns the optimal behaviors by observing the responses from the environment to sub-optimal control policies [34], has a great advantage in solving model-free problems. Adaptive dynamic programming (ADP), as an important branch of RL[35],is an effective method in solving the optimal control problem.For example,the RL and ADP methods were adopted in[25–27]to solve the optimal control problems for unknown linear systems. In these work, they addressed the delays of one channel,constant delays of multi-channels,and time-varying delays of multi-channels, respectively. While measurements were used to learn the optimal controllers in these works, disturbance rejection was not considered.Securing the control issue of unknown CPSs with actuator attacks and unmatched perturbation was addressed in [35].Although a model-free ADP algorithm was designed, the neural networks were introduced to approximate the value function and the identification error was added in the process of designing. The robust resilient control problem of the nonlinear system under actuator attacks was addressed in[32]by ADP techniques,although the system was partially unknown.Furthermore,the ADP method was also applied to solve the attack scheduling problem [36], the fault-tolerant problem[37]or privacy protection problem[38].However,to the best knowledge of the authors,there are few work on securing unknown CPSs against time-delay attacks.

Based on the aforementioned analysis, the adaptive output regulation problem for unknown CPSs under time-delay attacks in the S-C channel and the C-A channel is considered in this paper. A measurement feedback controller is designed only using control inputs and tracking errors.The model-free RL method is adopted to update the control gains online. Although the method of designing the controller is similar to the one in [25], the location of the delay is different, and attack-induced delays exist in two channels in our paper. Based on the measurement feedback controller,the closed-loop system could achieve both asymptotic tracking and disturbance rejection.The main contributions of this paper are summarized as follows.

1) It is proved that the performance index with delays is still quadratic, and the regulation equations with delays are obtained, which can ensure the linear output regulation problem to be solvable.

2)The measurement feedback controller can still realize the real-time closed-loop feedback control for the system,even though two channels suffer from time-delay attacks,and the tracking errors between the system outputs and the reference signals are asynchronous.

The rest of this paper is organized as follows.The problem formulation is stated in Sect.2. In Sect. 3, a measurement feedback controller with unknown model knowledge is designed, and the convergence of algorithms together with tracking performance is analyzed.Finally,a simulation example and the conclusion are presented in Sects.4 and 5,respectively.

Notations R denotes the set of all real numbers, Rndenotes then-dimensional Euclidean space, Rn×mdenotes the set of alln×mreal matrices.Iis the identity matrix.XTrepresents the transpose of the matrixX.X ＞(＜)0 denotes a positive-definite (negative-definite) matrix,X≥(≤)0 denotes a non-negative definite(non-positive definite)matrix.σ(X)denotes the set of eigenvalues of the matrixX.vec(X)is a vectorization operator that stacks each column of the matrixXto a column vector.

2 Problem formulation

In this section,the model of the CPS under time-delay attacks is obtained,and the augmented error system with measurement data is established.Then,the optimal output regulation of the CPS is described.

2.1 System model with attack-induced delays

Consider the following discrete-time system with unknown parameters:

whereE∈ Rq×qis an unknown Hurwitz matrix. This exosystem generates both the disturbanced(k)=Dr(k)and the reference signalw(k)=Fr(k)to the system.In fact,the exosystem is a description together with the disturbance and the reference signal,the specific origin of the system(1)and the exosystem(2)can be referred to the literature[39].In this paper,the reference signal is unknown and the tracking errore(k)∈R is the solely measurable output variable.Take the Internet of Vehicles as an example,the tracking errors can be measured by installing the sensors on the follower-cars,but the reference trajectory of the leader-car is unknown. Furthermore, according to the CPS structure shown in Fig. 1,when the system outputy(k)=Cx(k)and the control inputu(k)are sent to the controller and the actuator through communication networks,respectively,the S-C channel or C-A channel may suffer from the adversary time-delay attacks.The model of the time-delay attack can be described as

whered1,k≥0 andd2,k≥0 are the attack-induced delays in the C-A channel and S-C channel,respectively.Due to the constraint of attacks’cost,the dwell time of attacks is finite,hence the attack-induced delays are assumed to be bounded reasonably,i.e.,

Assumption 1 The delays induced by time-delay attacks are bounded.

From Assumption 1,we have 0 ≤d1,k≤d1and 0 ≤d2,k≤d2,whered1andd2are the maximal attack-induced delays in the C-A channel and S-C channel,respectively.It should be mentioned that the reference signal can be transmitted through the network or not in practice. Here, the security issue is mainly addressed that the attack is launched in the feedback or forward channel of the system,and the system output tracks a given reference signal,i.e.,the attack to the reference signal is not considered.For uncertain delays,the robust method is adopted in this paper, and the bounds of attack-induced delays are utilized to design the controller,more details are explained in Remark 1.Basing on the bounds of the attack-induced delays, the model of the system (1)under attacks can be described as follows:

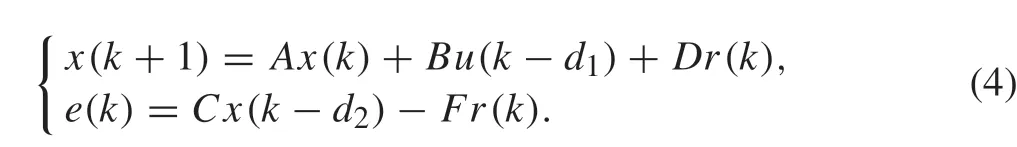
Next, the measurement data will be used to reconstruct the system model under time-delay attacks.

2.2 Augmented error system with measurement data

Due to the unmeasurable system state, the controller cannot be designed using the state feedback directly. Thus, an indirect way is to utilize the measurement information and designameasurementfeedbackcontrollerbyestablishingthe relation between the system state and the measurement information. In addition, let us defineξ(k)= [xT(k),rT(k)]T,then it follows from (2) and (4) that the augmented error system is written as

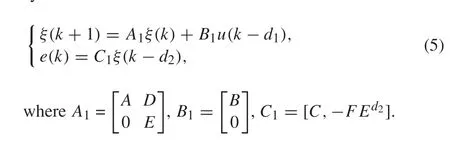
whereM1x∈Rn×nz,M1r∈Rq×nz,nz=2(n+q)+d1+d2.It follows from the above derivation thatξ(k+d1)traces back to the state ofξ(k-n-q-d2).Actually,the historical timek-n-q-d2can be extended to a general time pointk-N,as long asNis bigger thann+q+d2. From the similar derivation ofξ(k+d1)thatξ(k+d1-d2)has the following form:

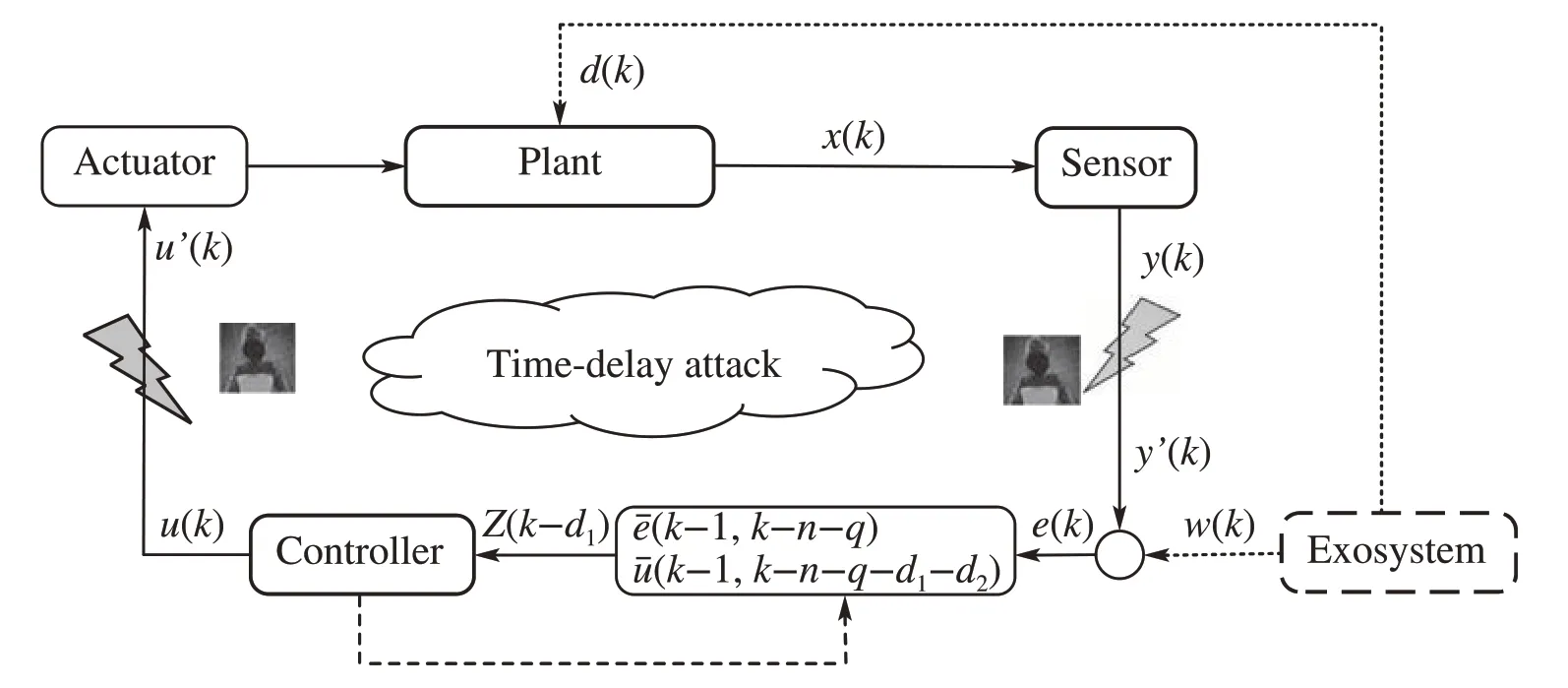
Fig.1 The frame of CPSs under attacks

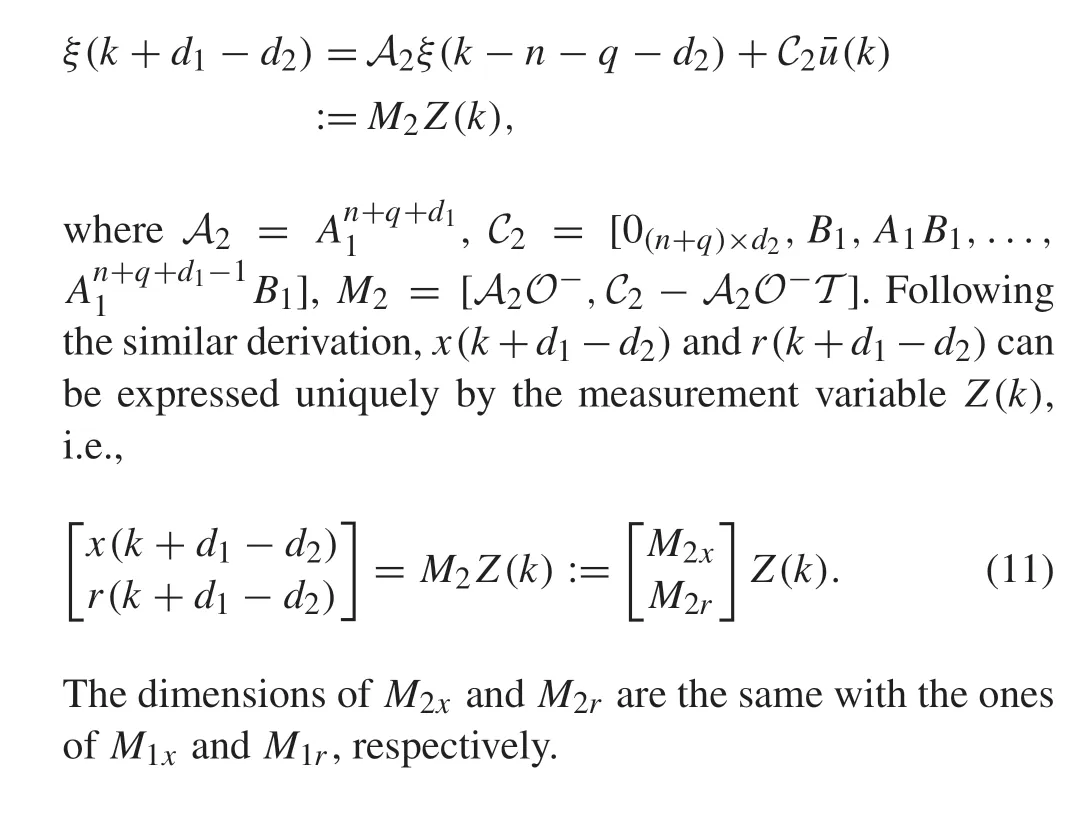
2.3 Linear output regulator

For the linear output regulator problem,the control input can be expressed as the standard formu(k)=-K x(k)+(K X+U)r(k)[40],whereKis obtained by solving an algebraic riccati equation(ARE),whileXandUare obtained by solving regulator equations.Inspired by the standard form of the controller,the following measurement feedback controller will be designed in this paper:

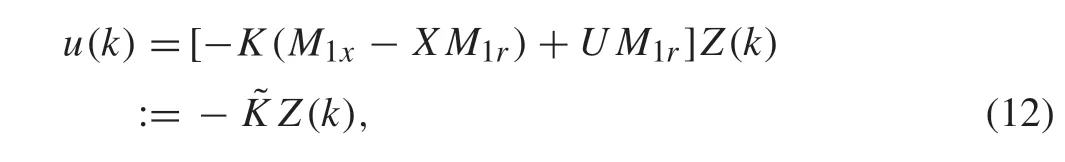
whereKsatisfies thatA-BKis a Schur matrix,X∈Rn×qandU∈Rm×qare obtained by solving the following regulator equations:

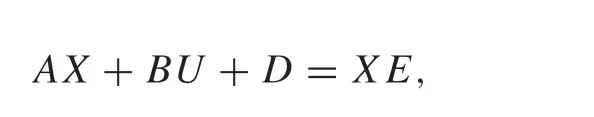
SinceA-BKis a Schur matrix,one has limk→∞¯x(k)=0,then,limk→∞¯u(k)=0,limk→∞e(k)=0 by(13)and(14).From the above analysis, the linear output regulation problem can be solved by applying the measurement feedback controller(12).At the same time,the open-loop form of the system(14)can be expressed as

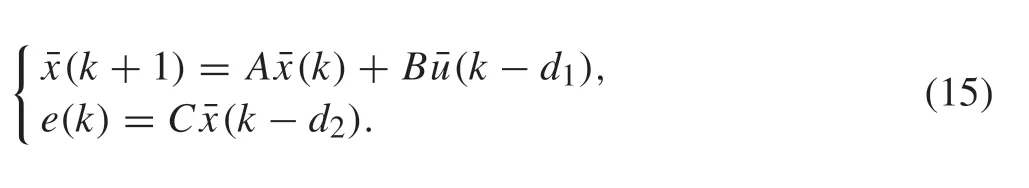
How to find the optimal controller (12) for the system under time-delay attacks in both channels will be solved in this paper. Here, the optimality is achieved by minimizing a predefined performance index or value function,which is chosen as

Remark 1The measurement feedback controller in this paper is designed according to the bounds of delaysd1andd2,which relate to the dimension of the controller gain. The designed controller is applied to the system where the attackinduced delays are less than the bounds, it means that the control components are redundant. In practice, this control scheme can be achieved through the time stamp at each data segment and a trigger which is introduced artificially in the control/actuator center.Take the S-C channel as an example,when the control center receives the data packet with time informationkat timek+d2,k(d2,k≤d2), the artificial trigger in the control center will not be trigged at once untilk+d2,and the data packet with time informationkwill be adopted atk+d2.If there are still other data packets arrived before the timek+d2,those packets will wait in the buffer.In this case,the proposed method can still deal with the case of time-varying delays.

Remark 2In practice, it is usually hard to obtain an exact system model, making it much difficult to design a secure controller. Fortunately, RL, which learns what to do from the environment so as to maximize a numerical reward signal [33], is a very effective tool to develop a model-free approach to update the control policy (action) and the performance index (reward). Based on the control inputs and tracking errors, the RL method is developed to update the controller gain in this paper.

3 Measurement feedback design with unknown model knowledge

Inthissection,ameasurementfeedbackcontrollerisdesigned to solve the problem(17)with unknown system parametersA,B,C,D,unknown exosystem parametersE,F,unmeasurable system statex(k),exosystem stater(k),and only the control inputs and tracking errors are utilized.

3.1 Controller design

Before presenting the algorithms, the following Lemma on the value function is introduced.

Lemma 1For the infinite-horizon output regulation problem,the reference signal is produced by the exosystem (2), then the value function(16)under any fixed stabilizing controller(13)can be expressed as

whereK j+1=(R+BTPj B)-1BTPj Ais obtained iteratively by solving the optimization problem (17) with no time-delays, i.e.,d1=d2= 0, then the system (15) is reduced to

Remark 3Notice that the ARE(30)is nonlinear,and much expensive computation is required to obtainP*. To reduce the computational cost, the policy iteration (PI) algorithm and the value iteration(VI)algorithm,which are two iterative algorithms in RL,are usually employed to approachP*approximately. When the time goes to infinity,PjandK jwill achieve toP*andK*with small neighborhoods,respectively. In this case,u*(k)=(-K*M1¯x+U M1r)Z(k)=- ˜K*Z(k), and it is equivalent to ¯u*(k-d1)= -K*¯x(k).This implies that the measurement feedback controller can stabilize the system(15)in an optimal sense.

Next,the measurement data will be used to learn the controller gain ˜K*.Let

Then,the online PI algorithm via the measurement feedback can be summarized by Algorithm1.

images/BZ_27_915_802_950_838.png

Note that the initial control policy needs to be admissible in the PI algorithm.To avoid the restriction,the VI algorithm is derived later.First,it is derived from(22)that

whereΘ= [θT(k0-d1),...,θT(k0+s-d1)]T,Φj=[(φj(k0))T,...,(φj(k0+s))T]T. Then, the controller gain can be updated by

Then,the online VI algorithm via the measurement feedback can be summarized by Algorithm2. The main differences between Algorithm 1 and Algorithm 2 are the requirement of the initial control policy and the convergence rate of the algorithm. If the initial control policy is admissible, Algorithm 1 can be chosen and its convergence rate is faster relatively than that of Algorithm 2.If the initial control policy is arbitrary, Algorithm 2 can be chosen, but the convergence rate of Algorithm2 will be slower relatively.

Remark 4It is known from (26) and (35) that ˜P∈R[2(n+q)+d1+d2+1]×[2(n+q)+d1+d2+1] is a symmetric matrix.To guarantee the application of the least square method,more than [2(n+q)+d1+d2+1]2/2 sample data should be collected before the learning process in Algorithm1 or Algorithm2.

Remark 5As usual, a probing noise is added into the input in the process of collecting data,the purpose is that the system can be excited sufficiently and the data can be collected diversely. Furthermore, the rank condition of matricesΨ jandΘcan be satisfied easily. Notice that this condition is necessary when ˜Pjis solved uniquely from(33)and(37)at each iteration.

images/BZ_27_1852_1786_1888_1823.png

3.2 Convergence and tracking performance analysis

In this subsection,a rigorous proof is presented for the convergence of above algorithms,and the tracking performance is analyzed after an approximate optimal controller is applied to the system.

Theorem 1The sequence{ ˜Pj}and{ ˜K j}obtained by Algorithm1 or Algorithm2 will converge to˜P*and˜K*as j→∞,where

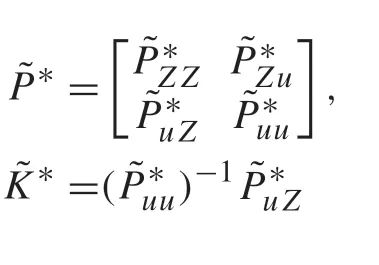
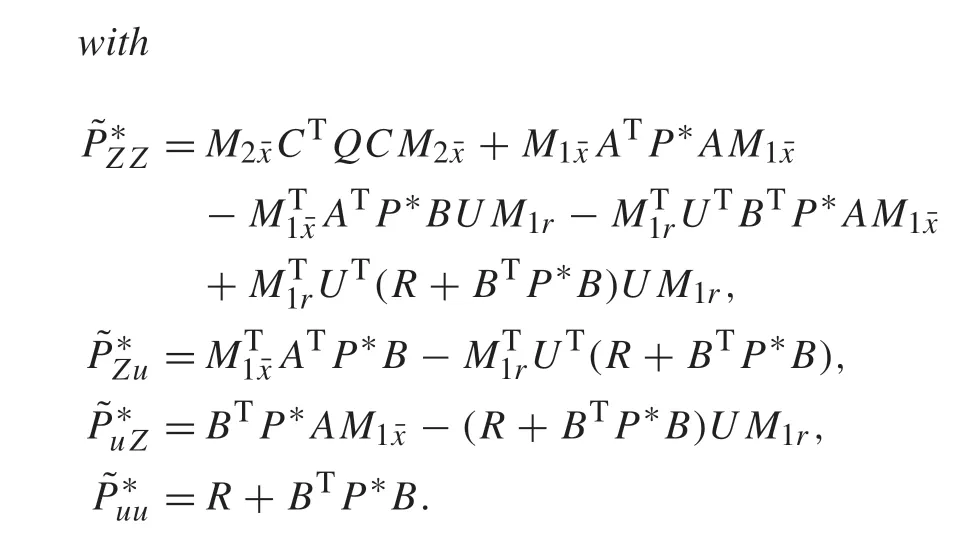
ProofFirst,consider the convergence of Algorithm1.The PI algorithm for solving the discrete-time ARE (30) had been presented in some literature such as [25–27], and the convergence was presented in[41].Particularly,Pjwas solved from

Based on the convergent Algorithms, the next theorem illustrates that the approximate optimal controller obtained by Algorithm1 or Algorithm2 can make the system achieve asymptotic tracking,even in the case of external disturbance and time-delay attacks.

Theorem 2The measurement feedback control policy u(kd1)= - ˜K j*Z(k-d1) can stabilize the system (15) and guaranteelimk→∞e(k)=0.

Since the sequence{K j}is convergent and the optimal controller gainK*can stabilize the system, i.e.,A-BK*is Schur. It implies that there is a small constant∈＞0, and the neighborhood withK*as the centerδ∈(K*),then given any approximate optimal controller gainK j*∈δ∈(K*),it is satisfied thatA-BK j*is Schur.Hence,limk→∞¯x(k)=0,which implies limk→∞e(k)=0.■

Remark 6In Algorithm1 and Algorithm2,the initial control policies are used to generate system trajectories during the period of collecting data.In the period of learning,the estimation policyuj(k)= - ˜K j Z(k)is updated by the collected data until certain precision of iterations is arrived. Hence,Algorithms1 and Algorithm2 are off-policy learning methods.

Remark 7For any attack-induced delays, the measurement feedback controller can be obtained by the proposed algorithms so long as that enough historical data is collected and the correlated conditions are satisfied.In most practical systems,the delay in the system cannot be too large due to the constraint of attack cost. When the delay exceeds certain threshold,the information is usually discarded,and this case can be regarded as DoS attacks, which will be one of our future works.

4 Simulation examples

In this section, the mass–spring–damper system (Fig.2) in[43,44]is used to validate the effectiveness of the proposed algorithms. In Fig.2,M,Landcrepresent the mass of the object,the stiffness constant of the spring and the damping,respectively.Then,thedynamicsprocessofthemass–spring–damper system is modeled by

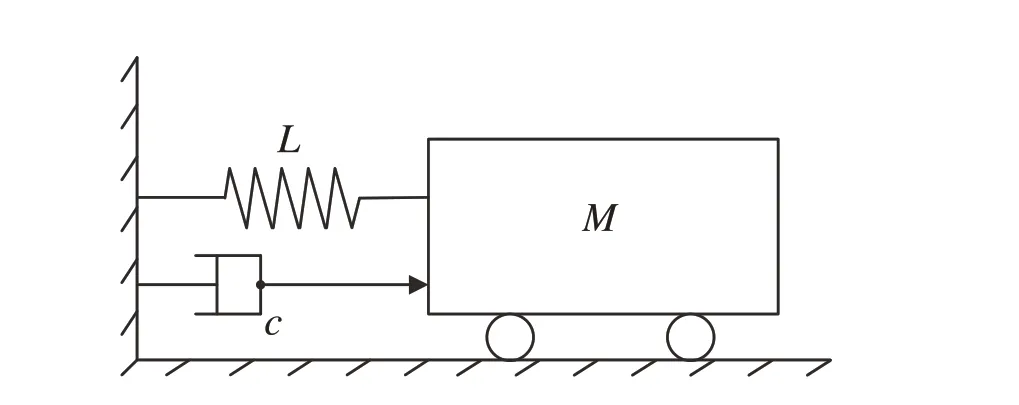
Fig.2 Mass–spring–damper system

The performance index is chosen as (16) withR= 1 andQ=100.The effectiveness of the proposed algorithms will be validated when time-delay attacks occur in different channels.

A.The case of time-delay attacks in the S-C channel

The time-delay attacks occur in the S-C channel,and there are attack-induced delays in the output.The initial stabilizing controller gain is chosen as

Afterk= 80, ˜K25is applied to the system,the trajectories of the system output and the reference are depicted in Fig.3.It is shown that the output tracks the reference signal asymptotically, which accords with the theoretical results in this paper.

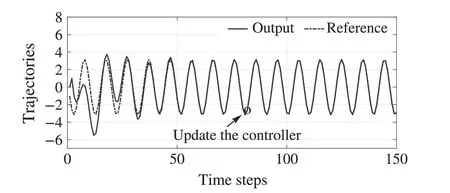
Fig.3 Case of time-delay attacks in the S-C channel

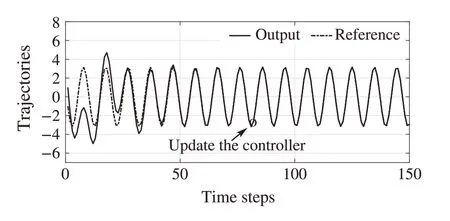
Fig.4 Case of time-delay attacks in the C-A channel

B.The case of time-delay attacks in the C-A channel

If time-delay attacks occur in the C-A channel,there will be attack-induced delays in the input.Algorithm2 is implemented,and the initial controller gain is chosen arbitrarily as follows:

C.Performance comparison

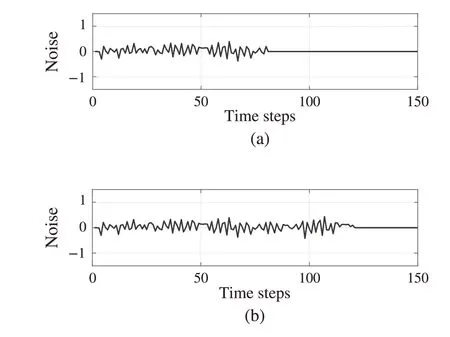
Fig.5 Exploration noise

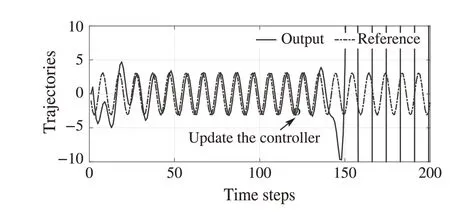
Fig. 6 Case of time-delay attacks in two channels with compared method

It is seen from the above simulations that the designed controller can achieve the adaptive output regulation in the presence of time-delay attacks. In fact, the case A in this paper was studied in [25], where the delay in one channel was addressed. The attack-induced delays in two channels are studied in this paper,and the maximum delays in different channels may not be the same.If the method of dealing with one-channel delay is applied to the system where twochannels suffer from adversary attacks, the system may be unstable,even be crashed.It is known that the dimensions of the designed controllers are different when the system with two-channel delays or one-channel delays.In the simulation,this fact has been illustrated by Fig.6. Before updating the controller,the relative data are collected along the system trajectory.When the learned measurement feedback controller is applied to the system without considering the delay in the S-C channel,the system trajectory will be far away from the reference signal.Hence,the learned controller with the case of input delay cannot stabilize the system with two-channel delays.

When the C-A channel and the S-C channel both suffer from time-delay attacks unfortunately,the measurement feedback controller in this paper will be employed,and Algorithm2 will be used to test the system performance.Choose an arbitrary initial controller gain as follows:

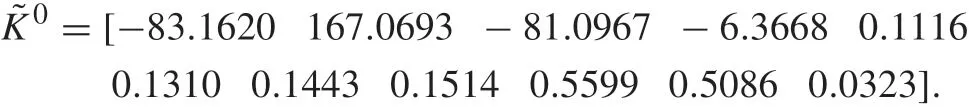
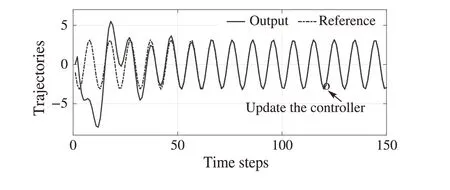
Fig.7 Case of time-delay attacks in two channels with our method

Then,the approximate optimal controller gain is learned after 40 iterations

Afterk= 120, ˜K40is applied to the system, Fig.7 shows the trajectories of the system output and the reference signal.Compared with Fig.6,it is clear that the trajectory changes dramatically after updating the controller.Fig.7 shows that the approximate optimal control policy can stabilize the system and make the system output track the reference signal asymptotically,which is as expected for the designed control method in this paper.

5 Conclusions

This paper studied the adaptive output problem for unknown CPSs under time-delay attacks which occur in the S-C channel and the C-A channel.Historical control inputs and tracking errors were used to design the measurement feedback controller, which could ensure the system to achieve the real-time closed-loop feedback control, even though the current measurements could be delayed due to timedelay attacks.The measurement feedback controller gain was calculated and updated online through solving the ARE iteratively with the RL method, and the system could achieve the asymptotic tracking and disturbance rejection. Simulation results on a mass–spring–damper system demonstrated the effectiveness of the proposed method.In the future,the proposed method can be extended to the cooperative output regulation with set-point attacks,secure control with attack detection.

Acknowledgements This work was supported by the National Natural Science Foundation of China(Nos.61973277, 62073292) and in part by the Zhejiang Provincial Natural Science Foundation of China(No.LR20F030004).