模袋混凝土干湿-冻融侵蚀孔结构的分形特征
2022-03-01孙浩然邹春霞薛慧君
孙浩然, 邹春霞,*, 薛慧君, 赵 泉, 武 军
(1.内蒙古农业大学 水利与土木建筑工程学院,内蒙古 呼和浩特 010018;2.内蒙古河套灌区乌拉特灌域管理局,内蒙古 巴彦淖尔 014400)
内蒙古河套灌区模袋混凝土衬砌常因季节性冻融和干湿交替而引起局部和大面积开裂、破坏等问题,严重影响其使用寿命和渠系建筑物的输水效率.研究发现,干湿-冻融耦合作用所致混凝土表面开裂、破坏等情况比单纯的冻融或干湿作用更为严重.当混凝土的相对动弹性模量达到相同的损伤度时,干湿-冻融耦合下损伤速率最快[1].这种损伤关系不是两者的简单叠加,而是一种超叠加效应关系,与混凝土组成和结构特征、干湿-冻融循环制度等因素有关.混凝土材料是一种具有复杂结构的复合材料体系,孔隙结构对其耐久性有着重要影响.将扫描电镜(SEM)和核磁共振(NMR)技术应用在混凝土工程中,有助于获得混凝土微观结构特征,为深入研究混凝土损伤情况提供了一种有效途径.而如何定量描述干湿-冻融耦合作用下的孔隙状态变化规律是研究模袋混凝土耐久性能亟待解决的问题.
分形理论作为研究物质不规则性和复杂现象的学科,与混凝土内部复杂的孔隙结构变化具有良好的契合性.近年来,许多学者尝试应用分形理论来研究混凝土孔结构变化.余志龙等[2]应用SEM 研究发现分形维数能够表征混凝土的微观结构;樊水龙[3]研究了在干湿循环下蚀变花岗岩的损伤程度与分形维数之间的关系,通过分形理论将SEM 图像从定性分析变为定量描述.张超谟等[4]进行了基于核磁共振T2谱分布的储层岩石孔隙分形结构的研究.Jin 等[5]基于分形理论发现气泡分布对混凝土抗冻性有重要影响.分形理论在混凝土工程中的应用显示出分形维数具有表征混凝土孔隙结构变化的能力.
本文总结前人的研究成果,将分形维数作为固定参数构建模袋混凝土干湿-冻融损伤模型.以分形维数的方法表征其内部损伤,探究不同维度下分形维数间的关联性.基于Coates 模型[6],计算出混凝土孔隙度、渗透率与分形维数间的数学关系.结合小波变换的回归估计,得到相对动弹性模量与渗透率的回归方程,提出以相对动弹性模量和分形维数为损伤指标的干湿-冻融损伤模型.
1 试验
1.1 试验材料
水泥采用蒙西P·O 42.5R 硅酸盐水泥;细骨料和粗骨料均取自巴彦淖尔市乌拉特前旗九公里料场;粉煤灰采用包头电厂的Ⅱ级粉煤灰;硅粉采用巴彦淖尔市乌拉特前旗玉石加工厂的固体废弃料,经研磨处理后满足混凝土试验要求;外加剂采用YE-NGX 萘系高效减水剂;拌和水采用普通自来水;干湿-冻融循环用水取自巴彦淖尔市乌拉特前旗的黄河水.模袋混凝土的配合比见表1.

表1 模袋混凝土的配合比Table 1 Mix proportion of mold-bag concrete kg/m3
1.2 试验方法
干湿-冻融循环试验试件为标准养护后的100 mm×100 mm×400 mm 棱柱体.根据内蒙古河套灌区气候特征和农业灌溉规律,选择干湿-冻融循环制度为5 次干湿循环、25 次冻融循环为1 次干湿-冻融循环.首先,将试件放入(55±5)℃烘箱中烘干11 h 后冷却1 h,然后置于黄河水中浸泡12 h 为1个干湿循环.5 次干湿循环后,将试块放入快速冻融机中进行25 次冻融循环,此为1 个干湿-冻融循环.重复做8 次干湿-冻融循环,每次干湿-冻融循环结束后测量试件的相对动弹性模量.分别在0、3、5、8 次干湿-冻融循环结束时,测定混凝土微观结构形貌和孔隙特征.采用S-4800 型扫描电子显微镜观测试件微观结构形貌,不同干湿-冻融循环次数(n)的SEM样品取自模袋混凝土内部的同一位置. 采用MesoMR23-60 型核磁共振仪分析混凝土孔隙特征,用金刚钻取芯机钻芯取样,尺寸为φ48×50 mm,真空饱水后开展核磁共振试验.
2 理论方法
2.1 SEM 分形维数计算方法
通过SEM 得到模袋混凝土干湿-冻融的微观图像,一方面可以直接观察其表面的结构和形态特征,另一方面可以利用分形维数将定性描述转为定量分析,以便揭示其损伤演变规律.计算图像分形维数的方法较多,如差分盒维数法、灰度插值法、双毯法等[7-8].本研究选择差分盒维数法对经历不同干湿-冻融循环次数试件的SEM 图像进行分形分析.运用Matlab软件计算SEM图像的分形维数,首先运用Otus法[9]计算出图像的最佳阈值,然后对图像进行二值化处理,将图像转化为只含有0和1的矩阵.SEM图像的像素尺寸逐渐减小,其对应的盒子累积个数相应增加.当盒子边长ε趋于0时,理论上盒子个数N(ε)趋于无穷.对ε和N(ε)分别取对数,求出lnN(ε)对lnε的斜率,其斜率的负值便是该分形图像的计盒维数DS,计算式如下[10]:
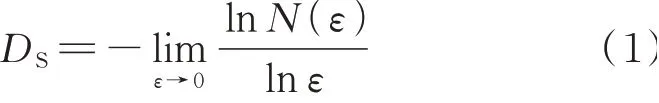
2.2 NMR 分形维数计算方法
通过NMR 得到模袋混凝土的微观孔隙结构特征,针对其特征参数计算得到的分形维数可定量反映孔隙结构状态.本研究根据NMR 的T2谱曲线特点推导出分形维数算法,并依据该算法分析不同孔隙结构的分形特征.混凝土中孔隙数目N满足下式[11]:
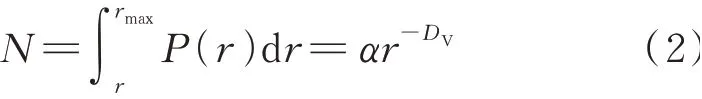
式中:r为孔隙半径;rmax为孔隙半径最大值;P(r)为孔隙分布密度函数;α为修正因子;DV为孔隙体积的分形维数.
此时核磁共振T2谱的分形算式为:
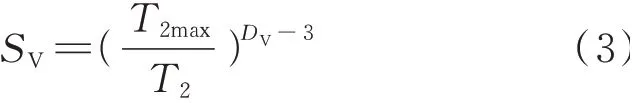
式中:T2为弛豫时间;T2max为最大弛豫时间;SV为横向弛豫时间小于T2时孔隙累积体积占总孔隙体积的比值.
将式(3)两边取对数得到近似分形几何算式:
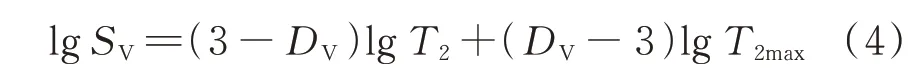
2.3 基于小波变换的回归估计方法
回归估计是在2组随机变量中找出关联,因此不存在理想的、均匀分布的变量空间.在大多数情况下需要对这种关联形式进行假定,即建立回归模型.小波变换能够对时间(空间)频率进行局部化,通过伸缩平移运算对信号逐步进行多尺度细化,最终达到高频处时间细分、低频处频率细分的能自动适应时频信号分析的要求.
3 结果与讨论
3.1 SEM 微观结构形貌的分形特性
模袋混凝土的SEM 图见图1.由图1 可见:干湿-冻融循环前试件微观结构呈鳞片状,存在部分不均匀孔隙结构,但过渡较为均匀,此时有水化产物生成;随着干湿-冻融循环次数n的增加,混凝土表面鳞片消失,团絮状的粉煤灰受黄河水中硫酸根离子侵蚀也逐渐消失,混凝土发生纤维化,表面由平整变得不平整,裂隙增多;特别是在干湿-冻融循环8 次后,纤维状产物变细,局部发生断裂,表明干湿-冻融循环对模袋混凝土造成不可逆的损伤.纤维状产物经能谱(EDS)分析(见图2)发现含有Ca、Fe、Al和Si等元素,证明该产物是钙矾石(AFt)[12].进一步,通过X射线衍射(XRD)分析(见图3)发现其主要成分为水化硅酸钙(C-S-H)凝胶、SiO2和AFt.

图1 模袋混凝土的SEM 图Fig.1 SEM micrographs of mold-bag concrete

图2 纤维状产物的EDS 图谱Fig.2 EDS spectrum of fibrous products
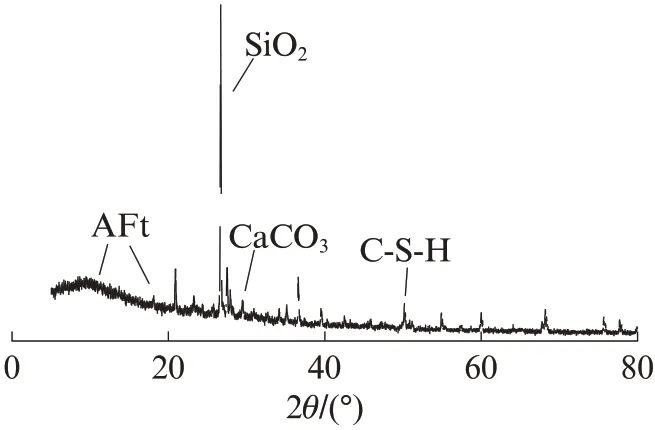
图3 纤维状产物的XRD 图谱Fig.3 XRD pattern of fibrous products
模袋混凝土的SEM 二值化图像见图4.利用图4得到二值化阈值及分形维数DS,结果见表2.由表2可见:SEM 图像的分形维数精度R2较高,能够较好地反映图像的非线性程度.
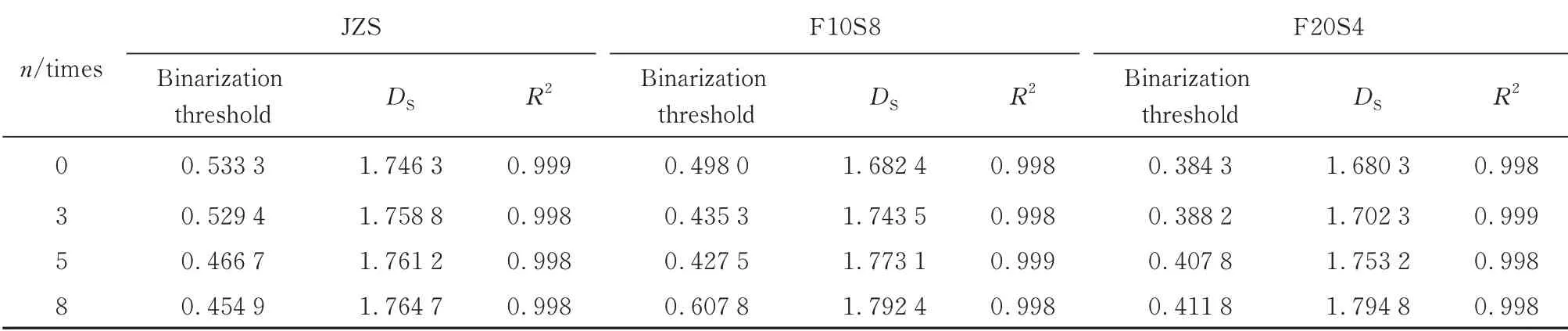
表2 SEM 二值化图像的分形维数结果Table 2 Results of fractal dimension from SEM binary images

图4 模袋混凝土的SEM 二值化图像Fig.4 SEM binary images of mold-bag concrete
对SEM 图中反映的损伤特征进一步定量分析,干湿-冻融循环8 次后部分纤维状产物发生断裂,分形维数随之增大.干湿-冻融循环作用后模袋混凝土的微观维数发生了变化,即分形维数随着干湿-冻融循环次数的不断增加而规律性增大.分形维数增大定量地表征了模袋混凝土内部裂隙、孔隙、构造层理等不规则性受干湿-冻融侵蚀作用趋于复杂化,混凝土损伤加重,耐久性能下降.同时,不同配合比模袋混凝土经历干湿-冻融循环作用后,其分形维数增加幅度和速度与其组成成分和内部结构有关.
3.2 模袋混凝土的孔隙结构及其分形特征
3.2.1 核磁共振孔隙结构
核磁共振试验可得到干湿-冻融循环作用下模袋混凝土的孔隙结构变化,T2谱图像中的弛豫时间与孔隙半径呈正相关,孔隙数量与峰面积相关.T2谱弛豫时间越长,则孔隙半径越大,孔隙水自由度越大,束缚流体饱和度越小,反之相反[13].弛豫时间和孔隙参数的关系可利用下式表示:

式中:ρ为与材料性质有关的弛豫强度;S为孔隙的表面积;V为孔隙体积.
根据核磁共振T2谱计算孔隙半径,将模袋混凝土的孔径划分为<0.1 μm、0.1~1 μm、1~10 μm、>10 μm 这4 个部分,试件JZS、F10S8、F20S4 各区间的孔隙分布如图5 所示.从图5 可以看出:随着干湿-冻融循环次数的增加,微孔呈增多趋势;0.1~1 μm 孔隙逐渐增多;而1~10 μm 孔隙逐渐减少;试件F20S4干湿-冻融循环8 次后,在大孔区间(>10 μm)内首次出现第3 个波峰.
3.2.2 基于NMR 技术的分形维数
将核磁共振T2谱对应的孔隙半径作为试验数据来计算孔隙体积的分形维数.在式(4)中,横向弛豫时间T2谱双曲线存在2 个不同的直线阶段.因此可由式(4)的斜率求得小于临界弛豫时间的分形维数DVmin和大于临界弛豫时间的分形维数DVmax,结果如表3 所示.
孔隙结构分布决定核磁共振分形维数的大小[14].混凝土中微孔大多与比表面积相关,而中孔、大孔更多与孔隙体积相关.从图5 和表3 可以看出,与孔隙体积呈更多相关性的中孔、大孔分形维数逐渐增加.孔隙水结冰融化的过程,相当于对孔壁不断地加荷卸荷.混凝土内部的微孔逐渐增多且部分孔隙转变为大孔隙,大孔隙内部大多为重力水,冻结过程中率先结冰,使渗透压力和静水压力的冻胀作用逐渐加大[15].中孔、大孔分形维数的变化,反映了干湿-冻融循环作用下模袋混凝土内部的损伤过程.图6 为欧式几何变换后不同维度下的分形维数.由图6 可见,经变换后SEM 图像的分形维数与核磁共振的分形维数相差不大,最大相差1.2%,平均差距为0.8%.说明不同维度下的分形维数具有一定的关联性.
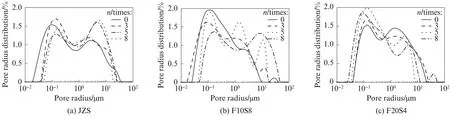
图5 试件JZS、F10S8、F20S4 各区间孔隙分布Fig.5 Pore distribution in different intervals of JZS,F10S8,F20S4 specimens
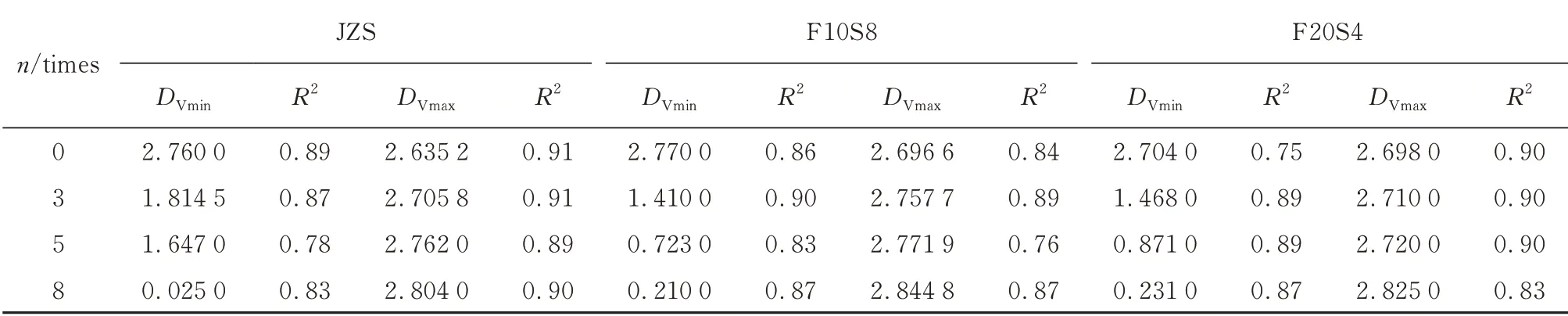
表3 基于核磁共振(NMR)计算的分形维数Table 3 Fractal dimension calculated based on nuclear magnetic resonance method
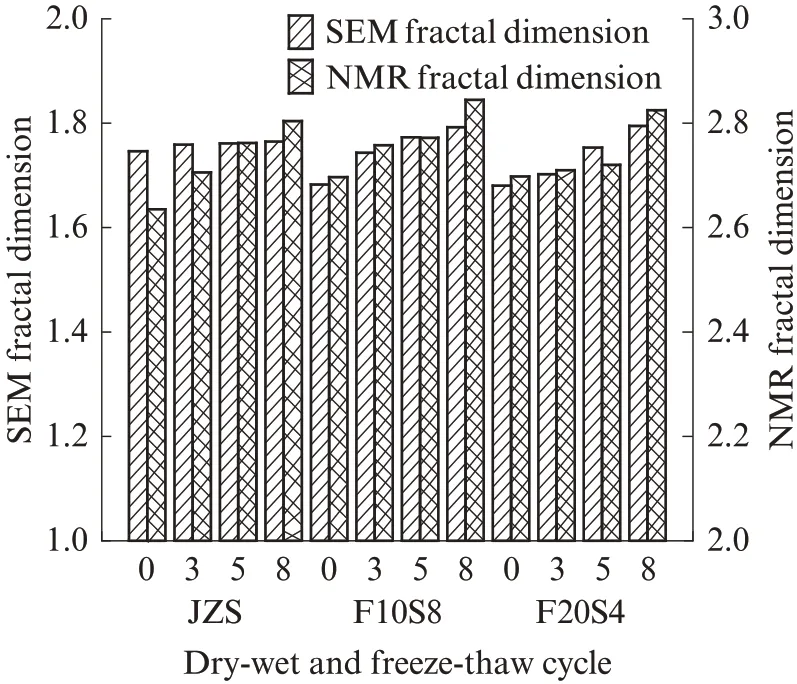
图6 不同维度下的分形维数Fig.6 Fractal dimension in different dimensions
3.3 体积孔隙度、渗透率与分形维数间的关系
欧式几何中n维物体在截面上相交为n-1 维,将欧式几何应用到分形几何中,分形体与截面相交,相交后分形体减小1 维.以DL、DS、DV分别从截线、平面、空间上表示分形体的维数,得到了分形维数表示的截线、平面、空间的数学关系[16]:
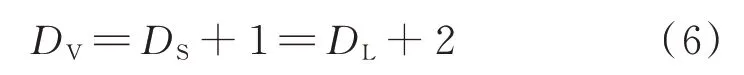
根据式(1)、(4)及面孔隙度、体积孔隙度的物理意义,得到分形维数与面孔隙度及体积孔隙度之间的关系:
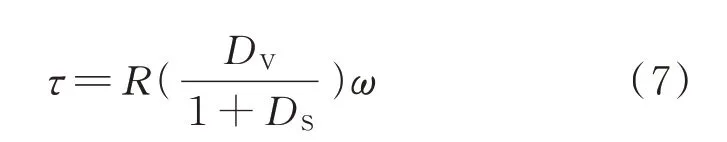
式中:τ为体积孔隙度;R为差维因子,利用试验数据回归拟合后得到R=1.05;ω为面孔隙度,等于SEM图像内孔隙面积与检测平面面积的比值.
采用Coates 模型[6]计算与混凝土水饱和度、孔隙度相关的混凝土渗透率:
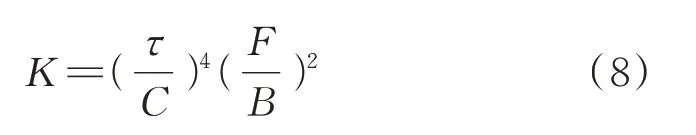
式中:K为渗透率;C为调整系数;F为自由水饱和度;B为束缚水饱和度.
将式(7)代入式(8),得到渗透率与分形维数、面孔隙度、水饱和度的关系:
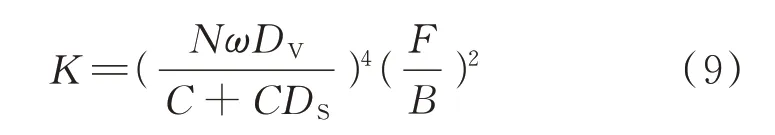
将试验所得混凝土水饱和度、分形维数等数据分别代入式(7)、(9),计算出混凝土的体积孔隙度和渗透率,计算值与实测值的比较见表4、5.
表4、5 显示,基于分形维数得到的体积孔隙度和渗透率计算值与实测值相差不大,误差均在6%左右,说明所建立的分形维数与混凝土体积孔隙度和渗透率的数学模型是合理的.

表4 体积孔隙度计算值与实测值的比较Table 4 Comparison of calculated and measured volume porosity%
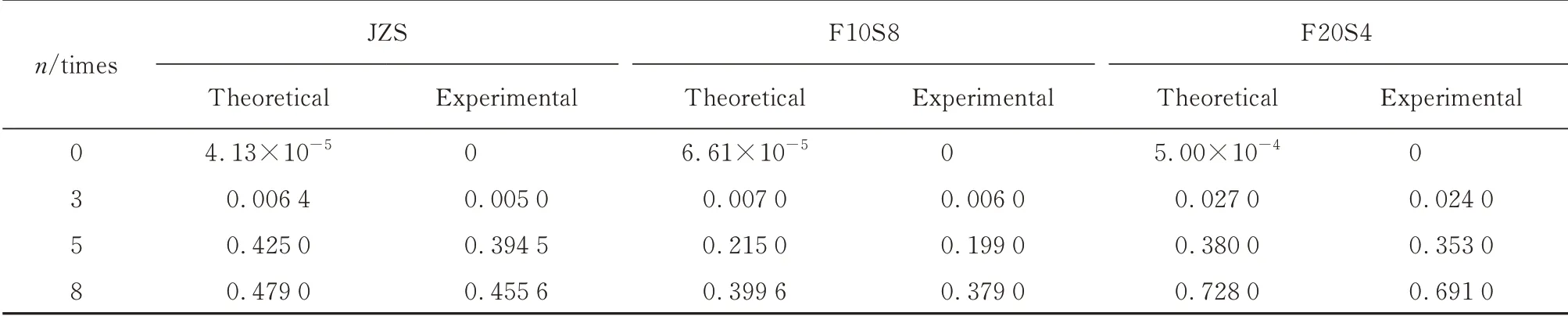
表5 渗透率计算值与实测值的比较Table 5 Comparison of calculated and measured permeability μm2
3.4 基于小波变换的回归估计
本研究选择干湿-冻融循环下模袋混凝土的相对动弹性模量和渗透率进行回归估计.借助Matlab软件的小波工具对相对动弹性模量所对应的渗透率进行小波分解,分解水平(level)为3,进行4 层分解,得到细节系数和近似函数.细节系数包含了试验过程中由于噪声或仪器本身引起的误差.试验测得的模袋混凝土相对动弹性模量见表6.
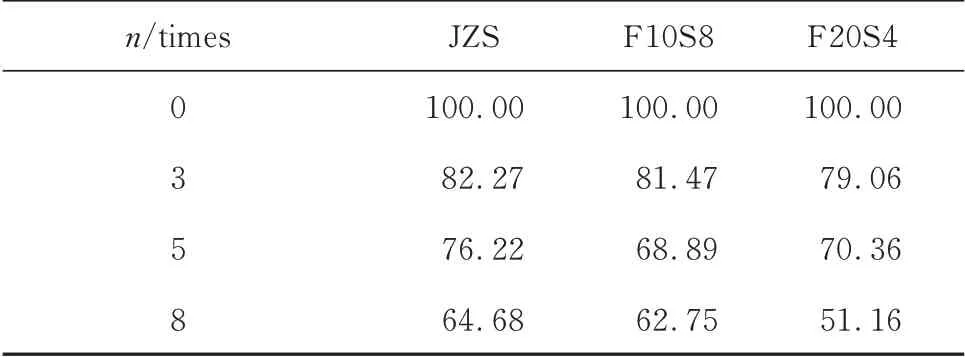
表6 模袋混凝土相对动弹性模量Table 6 Relative dynamic elastic modulus of mold-bag concrete%
依据近似函数,建立基于小波变换的回归方程:
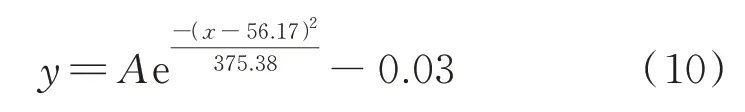
式中:y为渗透率;x为相对动弹性模量;A为相关系数.
将式(9)代入式(10),得到相对动弹性模量和分形维数、饱和度之间的关系:
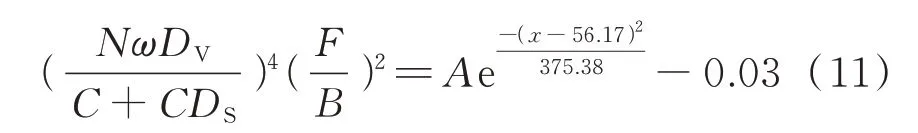
将基于小波变换回归估计建立的相对动弹性模量与渗透率的回归方程(式(11))和试验结果进行比较,如图7 所示.由图7 可见,该回归方程与试验结果基本吻合,说明依据分形理论,以相对动弹性模量为损伤指标建立的干湿-冻融损伤模型是合理的.
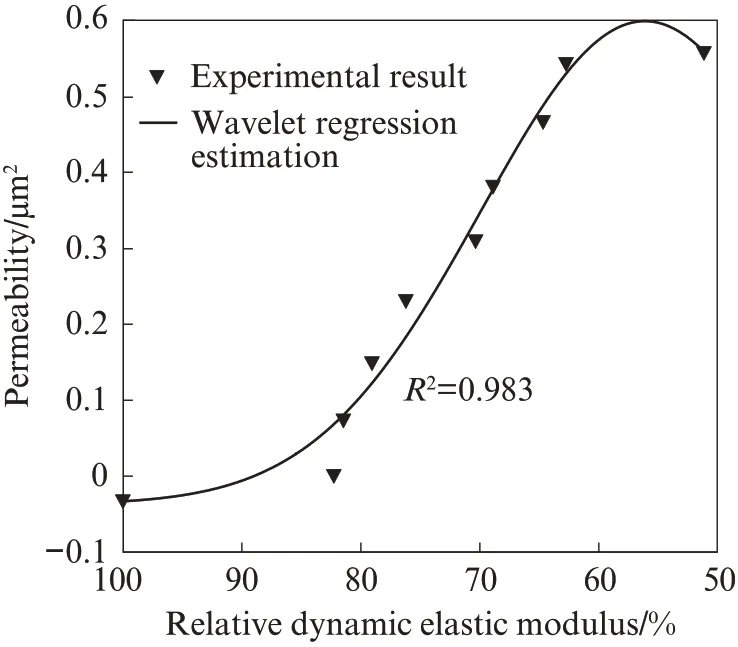
图7 回归方程与试验结果对比Fig.7 Comparison between regression equation and experimental results
4 结论
(1)分形维数可以定量描述不同干湿-冻融循环次数下模袋混凝土的微观损伤情况.结合扫描电镜和核磁共振试验结果,分形维数随着模袋混凝土干湿-冻融循环次数的增加而增大,表明模袋混凝土的损伤程度体现为分形维数的增大.
(2)基于核磁共振T2谱,建立了横向弛豫时间的分形公式,根据T2谱分布特征计算出的分形维数DV能够表征干湿-冻融循环下模袋混凝土内部孔隙的演变规律.并将不同维度下的分形维数通过欧式几何的概念建立联系,发现扫描电镜下二维图像的分形维数与核磁共振下三维孔隙结构的分析维数具有很高的关联性,其平均差距为0.8%.
(3)利用分形理论将不同试验结果联系起来,建立了模袋混凝土体积孔隙度、渗透率与分形维数的数学关系,计算值与试验结果基本吻合,可以预测混凝土的孔隙度和渗透率.
(4)引入小波变换的回归估计,建立了相对动弹性模量与渗透率的回归方程,推导出以分形理论为基础的损伤模型,为深入研究模袋混凝土干湿-冻融损伤机理奠定了基础.
