同类变级配沥青混合料矿料间隙率模型及分析
2022-03-01刘树堂薛志超陈鲁川曹卫东
刘树堂, 栾 娟, 薛志超, 陈鲁川, 曹卫东,*
(1.山东大学 齐鲁交通学院,山东 济南 250002;2.山东高速集团有限公司,山东 济南 250000)
在热拌沥青混合料(HMA)的体积法配合比设计中,矿料间隙率(VMA)是选择级配的决定性指标.目前中国采用的马歇尔设计方法直接以适宜沥青用量的VMA 是否符合技术标准最小值作为级配选择的依据,而美国Superpave 设计方法以空隙率为4%时的VMA 是否满足要求来选择级配.VMA 又是确定最佳沥青用量的关键参数,对空隙率(VV)和沥青饱和度起着决定性作用,因此必然对HMA 的性能产生直接和间接的影响.鉴于此,道路工作者对其进行了广泛研究.郝培文等[1]主要基于国外研究成果综述了VMA 最小标准值确定的发展历程、标准值大小和制定依据等方面可能存在的问题或争议;Pouranian等[2]指出,适当的VMA 是保证沥青混合料耐久性和抗车辙性能的重要因素;Al-Shamsi 等[3]认为最低要求的VMA 是必要的,较低的VMA 会降低混合料的低温性能,导致纵向裂纹与龟裂增加;Kandhal 等[4]、Coree[5]及Anderson 等[6]的研究表明,满足VMA 要求有时较为困难,同时发现具有较高VMA 的粗级配沥青混合料性能较差.VMA 受到集料棱角性、粗集料表面纹理特性、矿料密度和级配、压实工艺等诸多因素的综合作用,在料源、压实工艺等条件确定的情况下,应着重关注级配对VMA 的影响.Mallick 等[7]对5种集料公称最大粒径的沥青混合料进行试验发现,2.36 mm 筛孔通过率对VMA 有显著影响;王端宜等[8]基于大量试验的统计分析表明,VMA 与2.36 mm 筛孔通过率有显著的相关性,总体趋势是VMA 随着2.36 mm 筛孔通过率的增大呈线性增大;李彦伟等[9]通过大量试验发现,最佳油石比下粗细集料(以2.36 mm为粗细集料分界筛孔尺寸)比例或细集料用量对VMA 的大小有决定性影响,VMA 随着细集料含量的增加呈现有谷值凹形曲线变化;黄继成等[10]进行的SMA-13 试验表明,VMA 随着2.36 mm 筛孔通过率的增大而增大,而对OGFC-13 和AC-16 而言,VMA 则随着2.36 mm 筛孔通过率的增大而减小.可见,众多学者对各类变化级配沥青混合料的VMA 变动规律开展了大量研究,得到了一些直观、有益的结论,但对VMA 变化趋势的探索主要是基于对大量试验数据的统计分析手段进行的,尚未对变化趋势背后的机理或因果关系予以研究.因此,建立不同级配沥青混合料VMA 的物理模型十分必要,借助物理模型可从本质上揭示上述各种VMA 变化曲线背后的物理机制.这对于沥青混合料配合比优化设计及其性能保障而言具有十分重要的理论与工程意义.
1 同一沥青混合料VMA 与VCAmix的物理关系
对于确定级配和沥青用量的压实沥青混合料试件而言,不论是HMA 还是沥青玛蹄脂碎石混合料(SMA),其矿料间隙率1)本文涉及的间隙率均为体积分数;含量、通过率、油石比等均为质量分数.均可由式(1)计算:
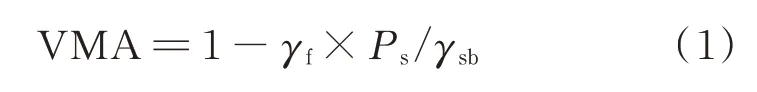
式中:VMA 为矿料间隙率;γf为沥青混合料试件的毛体积相对密度;Ps为矿料含量;γsb为矿料的合成毛体积相对密度.
对于SMA 试件而言,粗集料间隙率是一个重要的体积指标,由式(2)计算:

式 中:VCAmix为SMA 试 件 的 粗 集 料 间 隙 率;Pca为SMA 试件中的粗集料含量,Pca=Ps×(1-Pcf),其中Pcf表示粗细集料分界筛孔通过率,按照JTG E42—2005《公路工程集料试验规程》给出的定义,粗细集料分界筛孔尺寸为2.36 mm;γca为粗集料的合成毛体积相对密度.
尽管VCAmix首先是针对SMA 提出的,但显然也可推广至一般HMA 试件,只是HMA 试件的VCAmix较大而已.于是,对同一级配的压实HMA 试件,基于式(1)、(2)进行数学推导,可得到该种试件VMA 与VCAmix之间的物理关系式:
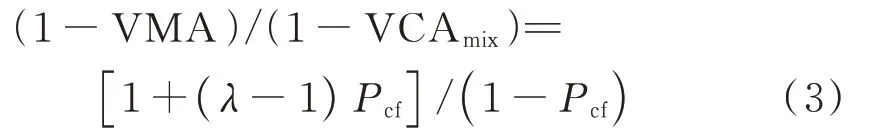
式中:λ=γca/γfa,其中γca、γfa分别为粗集料、细集料的合成毛体积相对密度.
2 同类变级配沥青混合料VMA 与VCAmix的物理关系
本文约定,同类变级配沥青混合料是指级配矿料的(公称)最大粒径相同,但级配曲线位置不同的几组沥青混合料.工程中热拌沥青混合料的配合比设计实质就是在同类变级配沥青混合料(如AC-25)中,通过试验寻找一种体积指标与路用性能均满足要求的配合比的过程.式(3)中如果Pcf发生变化(即粗、细集料含量发生变化),则VMA 与VCAmix也必然发生变化,同时系数λ也会发生轻微改变.为便于表述,将变量Pcf用x代换,则式(3)变为:
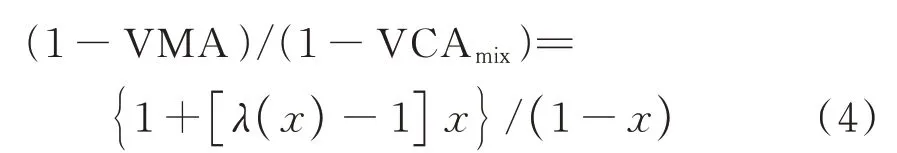
式中:VMA、VCAmix分别是粗细集料分界筛孔通过率为x时,同类变级配沥青混合料的矿料间隙率与粗集料间隙率,均为x的函数.
一般情况下,粗集料的相对密度大于细集料和矿粉的合成相对密度,但两者的比值十分接近1.为简化研究,可近似认为λ(x) =1,尽管这会带来一定偏差,但分析表明不会影响最终的规律性结论.于是式(4)可简化为:
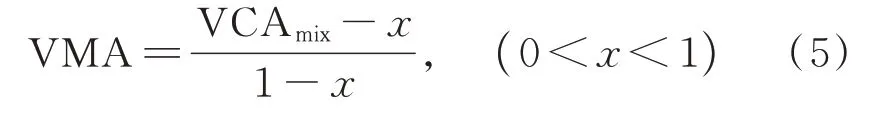
式(5)属于物理型模型,具有普适性,其普适性源于式(1)、(2).基于数学意义,广义而言,式(5)中x的取值可在开区间(0,1)内,但结合工程常用沥青混合料(如AC-13/20/25 和SMA-13 等)的级配范围,当认定x为2.36 mm 筛孔通过率时,则x∈[0.2,0.4]具有较好的取值代表性.
由式(5)可知,VMA 与x、VCAmix有关,而x又影响着VCAmix,因此VMA 是关于x的复杂函数.这深刻地表明了粗细集料分界筛孔通过率对VMA 的重要影响,也从内在机理上揭示了诸多试验研究中发现的VMA 随着粗细集料分界筛孔(譬如尺寸为2.36 mm)通过率的变化而呈现出规律性变化的根本原因.
基于式(5),如果进一步考察VMA 随着x的变化规律,则还需分析x对VCAmix产生的影响,此时需考虑实际级配矿料中细集料颗粒对粗集料颗粒的排列是否产生干涉作用及干涉作用的性质.谭忆秋等[11]研究表明,混合料中主骨架粒径为4.75~9.5 mm 时,最小的集料干涉粒径为1.18 mm,因此,级配矿料中存在的粒径为1.18~2.36 mm 的细集料对粗集料的排列产生干涉作用就成为必然,且细集料用量越多,这种干涉作用越强,导致粗集料间隙率越大.因此,一方面,结合工程中常用的AC-13/20/25 的级配特点,选择2.36 mm 作为粗细集料分界筛孔尺寸具有合理性;另一方面,需通过试验发现细集料对粗集料间隙率会产生何种函数类型的增大作用.能起到增大作用的函数在理论上不外乎有线性和非线性2 类,故可将VCAmix看作x的增函数,分别按线性、非线性予以进一步分析.
2.1 VCAmix为线性增大时VMA 模型及分析
2.1.1 VMA 模型建立
令 VCAmix=ax+b,(a>0),将 其 代 入式(5)得:
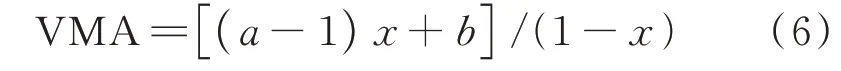
式中:a、b为回归系数,基于试验数据通过回归分析确定.模型(6)适用于细集料用量对粗集料间隙率产生线性增大作用的情形.
2.1.2 VMA 模型表示的可能变化规律
式(6)两端分别对x求1 阶与2 阶导数,得:
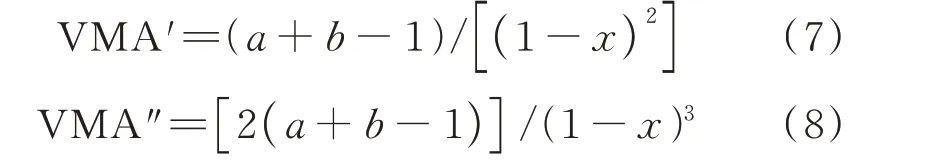
分析a、b可能的取值,不可能有(a+b)=1,否则VMA'=0,表明关键筛孔通过率变动对VMA 无影响,这与事实不符.因此,只能是(a+b)>1 或(a+b)<1:若(a+b)>1(譬如a=1.200,b=0.050),由式(7)、(8)可知,VMA'与VMA″同时大于零,则式(6)表示为上升的凹形曲线;若(a+b)<1(譬如a=0.600,b=0.230),则VMA'与VMA″同时小于零,式(6)表示为下降的凸形曲线,见图1.
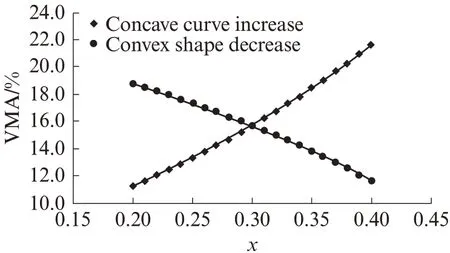
图1 VCAmix线性增大时可能的VMA 曲线Fig.1 Possible VMA curve morphology when the VCAmix increases linearly
上述分析表明,若VCAmix随x呈线性增大的话,VMA 不可能有其他的曲线,只能是图1 中2 条曲线之一;具体形态则取决于回归系数a、b之和是大于1还是小于1.
2.2 VCAmix为指数函数增大时VMA 模型及分析
2.2.1 VMA 模型建立
非线性函数的类型较多,考虑到若增大粗细集料分界筛孔通过率x,将同时减小粗集料含量(1-x),选择以指数函数表示x对VCAmix的增大作用应是合理的;试验也发现VCAmix确实随着x的增大具有指数函数的增大趋势.因此,令VCAmix=aebx,将其代入式(5),得:
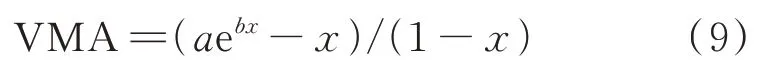
式中:a,b为通过试验确定的回归系数,a>0,b>0.模型(9)适用于细集料用量对粗集料间隙率产生指数函数增大作用的情形.
2.2.2 VMA 模型表示的可能变化规律
为便于进一步分析,需将式(9)分子中的指数函数在x=0 处作Taylor 级数展开,展开式应满足精度要求.由于常用AC 类材料在2.36 mm 筛孔通过率的上限一般不超过40%,计算表明,当指数函数中的系数b≤3 时,展开式中最高到x的3 次方即能达到较好的精度,如b=3,在x=0.2、0.4 时展开式的相对误差分别为0.34%、3.38%.在x=0 处,3 次Taylor 级数展开式为:
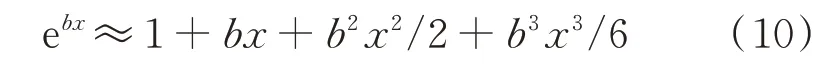
将式(10)代入式(9),得到:
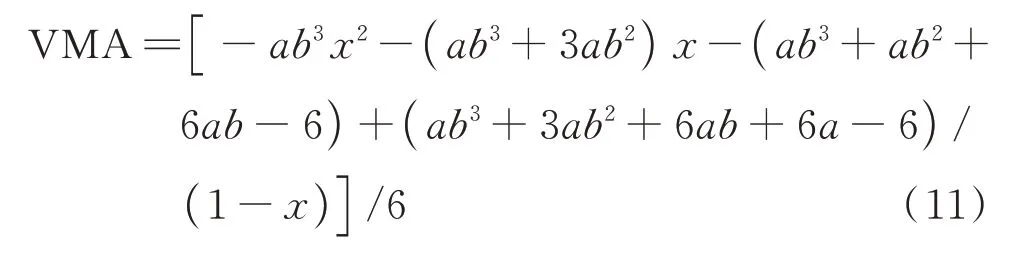
式(11)两端分别对x求1 阶与2 阶导数,得:
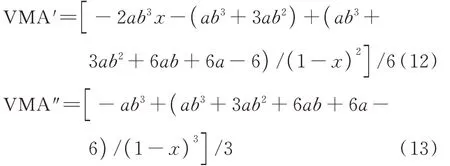
在x定义域内,根据VMA'、VMA″的正负,可判断式(9)表达的可能曲线.
(1)VMA'<0、VMA″>0 一并成立的可能性.基于式(13),当VMA″>0 时,得到:
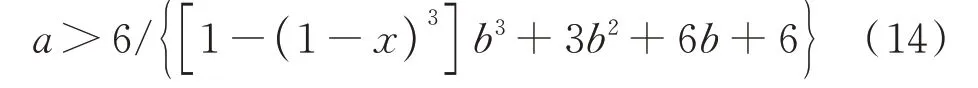
联 立 式(12)<0、式(13)>0,得 到ab2(x-1)2(xb+1) >0,因a>0,b2(x-1)2>0,所以有:

显然,式(14)与(15)能同时成立,则式(9)表示VMA 为下降的凹形曲线就成为可能.
仿照上述,再分别对VMA'>0、VMA″>0 一并成立;VMA'<0、VMA″<0一并成立;VMA'<0、VMA″>0 与VMA'>0、VMA″>0 一并成立的可能性进行分析,结果表明VMA 为上升的凹形曲线、下降的凸形曲线、有谷值的凹形曲线(或类似开口向上的2 次抛物线)均是可能的,但限于篇幅,此处不赘述.
(2)VMA'>0、VMA″<0 一并成立的可能性.根据式(12)、(13),得到3ab2(x-1)2(xb+1) <0,由于a>0,因此有xb+1 <0,即b<-1/x,为负,这与b>0 相矛盾,因此,在x∈(0,0.4]范围内,VMA不可能为上升的凸形曲线.
(3) VMA'>0、 VMA″<0 与 VMA'<0、VMA″<0 一并成立的可能性.基于第(2)条的分析,因不存在VMA'>0 及VMA″<0,故VMA 变化不可能出现含有峰值的凸形曲线.
综上分析,在通常的级配范围及可能的VMA 值域内,指数函数表达的VMA 可能的曲线有图2 所示的4 种情形.图2(a)中的凹形下降曲线、凸形下降曲线 分 别 基 于a=0.250、b=1.600 和a=0.300、b=1.140 绘制,凹形上升曲线基于a=0.165、b=2.950 绘制;图2(b)中的曲线基于a=0.200、b=2.200 绘制.

图2 VCAmix按指数函数增大时可能的VMA 变化曲线Fig.2 Possible VMA curve morphology when the VCAmix increases exponentially
图1、2 中,若VMA 值随着x的增大而下降,则表明沥青混合料由骨架空隙型向骨架密实型趋近;若VMA 值随着x的增大而上升,则表明沥青混合料达到骨架密实状态后进入悬浮密实状态,且粗集料悬浮程度逐渐增大.
2.3 VMA 模型选择
在近似认为粗细集料的密度相等时,式(5)即为同类变级配沥青混合料矿料间隙率的理论模型.因其是基于确定配比沥青混合料的VMA 与VCAmix的计算公式推导而来,因而该模型具有普适意义.同理,基于式(5)进一步得到的式(6)与式(9)也具有各自适用的物理基础.
图1、2 展示的为式(5)理论上可能出现的各种形态VMA 曲线.由式(6)、(9)可知,对于确定的同类变级配沥青混合料而言,所出现的曲线形态取决于压实沥青混合料中粗细集料分界筛孔通过率x对VCAmix产生的影响是线性增大还是非线性增大.总体而言,与式(9)对应的图2(b)变化规律具有更广泛的意义,因而将式(9)作为同类变级配沥青混合料的VMA 模型应具有更好的代表性.
3 模型验证
3.1 试验及结果分析
选用AC-25 中5 种级配作为模型验证的工程案例,5 种级配的2.36 mm 筛孔通过率依次为16.0%、20.0%、24.2%、30.0%、36.0%,对应的最佳油石比分别为4.09%、4.11%、4.14%、4.17%、4.20%;基于马歇尔压实工艺制件,获得各级配沥青混合料试件的VMA 和VCAmix.VMA 的实测曲线见图3.
3.2 预测模型及预测结果分析
分别按VCAmix与x之间为线性函数、指数函数进行回归分析,得到在显著性水平α=0.001 下的有效回归方程,并将其分别代入式(5),得到式(16)、(17).据此计算获得预测的VMA 曲线,也列于图3.
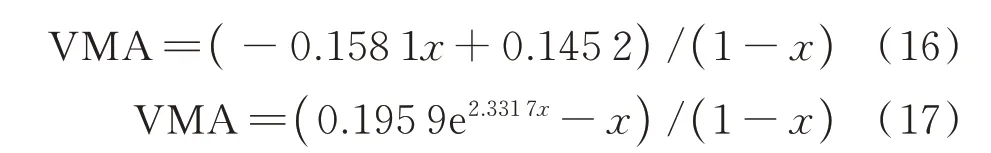
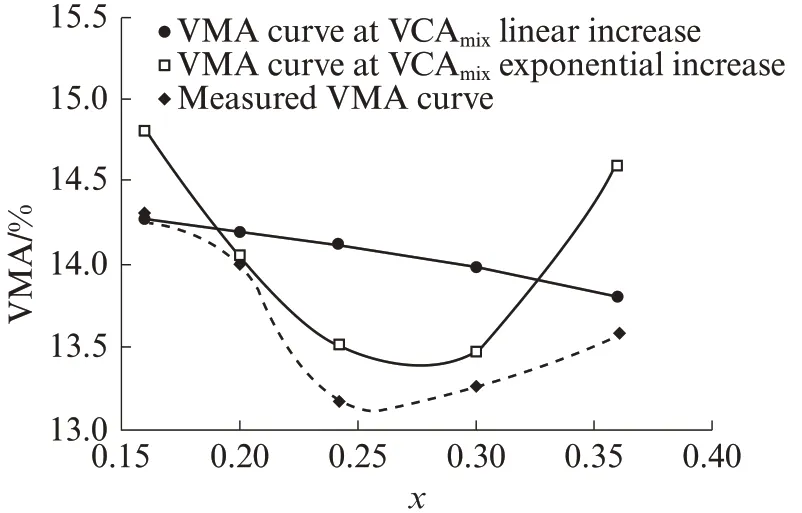
图3 不同模型预测的VMA 曲线与实测VMA 曲线对比Fig.3 Compared with the measured VMA curve and prediction VMA curves of different models
图3 表明:实测VMA 曲线呈现有谷值的凹形曲线变化;当把细集料对VCAmix的增大作用看作线性函数时,预测得到的VMA 为凸形下降曲线,这与实测曲线的变化趋势明显不符;当把细集料对VCAmix的增大作用看作指数函数时,预测的VMA 变化规律为类似开口向上的2 次抛物线,则与实测曲线的变化趋势一致.这表明,就本案例AC-25 而言,将VCAmix随着2.36 mm 筛孔通过率的增大看作以指数函数变化是符合实际的.另外本文发现,尽管式(16)中分子部分的线性关系式也具有极高的显著性,但据其得出的结论却与实际结果不吻合,说明某些情况下基于有效回归方程推出的结论可能存在错误的风险.
根据式(17)得到VMA 最小值为13.4%时的粗细集料分界筛孔通过率x约为0.275,即27.5%附近;预测的VMA 最小值与图3 中实测曲线的最小值13.2%~13.3%有0.1%~0.2%的偏差,对应VMA最小值时的x有约2%的偏差;偏差主要是由近似认为粗细集料相对密度之比λ(x) =1 及回归分析误差造成.在满足VMA 最小值技术标准的前提下,较小的VMA 具有较高的抗车辙性能;因此,式(17)可作为AC-25 类混合料的经验公式参考使用,据其获得高温性能较好的级配;同时,在进行沥青混合料级配设计时,可用来预测VMA 大小排序,必要的排序预测对确保设计出合理的级配具有重要意义.
VMA 呈现含有谷值凹形曲线的变化规律具有典型代表性,文献[9]中的大量试验也验证了该类变化趋势.
4 结论
(1)建立了同类变级配沥青混合料VMA 的物理模型.模型表明在其他条件确定时,沥青混合料中细集料对粗集料间隙率的增大作用性质及粗细集料分界筛孔通过率是影响VMA 变化规律的2 个决定性因素,从而诠释了诸多试验中发现的粗细集料分界筛孔(譬如尺寸为2.36 mm)通过率对VMA 有突出影响的原因.
(2)对物理模型的理论分析表明,在一定的级配范围内,随着粗细集料分界筛孔通过率的增大,同类变级配沥青混合料的VMA 在理论上可呈现凹形曲线下降、凸形曲线下降、凹形曲线上升及有谷值的凹型曲线(或类似开口向上的2 次抛物线)等多种可能的变化趋势,但不可能呈现有峰值的凸形曲线变化规律.
(3)对AC-25 而言,将2.36 mm 作为粗细集料分界筛孔尺寸是合理的,认为细集料对粗集料间隙率产生指数函数的增大作用符合实际;在进行AC-25矿料级配设计时,给出的模型可用于预测不同级配混合料的VMA 大小排序,同时还可获得VMA 最小值的类骨架密实型级配,该级配的分界筛孔通过率约为27.5%.
