基于稀疏降噪自编码的电能质量扰动识别研究

邓 鹏，张良力，2，王 斌，2

(1. 武汉科技大学信息科学与工程学院，湖北 武汉 430081；2. 武汉科技大学人工智能学院，湖北 武汉 430081)

1 引言

由于大量非线性负载、电力电子装置、可再生能源转换设备和微电网的接入，电网电能质量受到巨大冲击。为保证电网运行稳定和用户取电安全，必须监测并优化电网电能质量。而从海量、高维的电网电能信号中正确识别各种扰动数据，是进行电网电能质量后续监测及动态补偿的重要前提[1]。

特征提取、分类识别是电能质量扰动识别的两个主要部分[2]。传统特征提取方法有傅里叶变换、小波变换、S变换及希尔伯特-黄变换等[3-4]。其中傅里叶变换稳态信号分析能力强，但无法有效提取暂态信号局部特征；S变换运算过程繁杂，所提取的特征对噪声不敏感且精度不高；多种类小波基的选取问题增加了小波变换特征提取预处理时间；希尔伯特-黄变换需要额外处理以抑制模态混叠现象。分类识别常见方法如K近邻法、支持向量机(SVM)、决策树及极限学习机等，属于浅层分类模型，应对复合多重扰动时，分类器精度易受到限制[5]。

通过模拟人脑智能化处理海量、高维信息的深度学习方法，凭借优秀的数据内部信息提取能力，在电能质量扰动识别领域受到学者关注，如文献[6]采用卷积神经网络，文献[7]采用深度置信网络进行电能扰动信号识别实验，均得到较好的分类效果。当分类识别对象含噪点信息时，卷积神经网络易将其归类为新类型对象，抗噪性不高；深度置信网络形成多层神经网状结构时，缺少有效的减层手段，从而产生累积误差。

自编码模型通过编码、解码过程，将高维数据压缩并储存，使用已训练的特征向量作为输入，初始化分类器并构建整合网络，经过反向微调后，能记忆各类电能质量扰动抽象特征，进而有效区分输入样本种类，在电网扰动信号识别处理方面具有潜在优势。为进一步挖掘电能质量扰动信号内部特征并有效减少误差累积量，本文提出一种基于数据驱动的稀疏降噪自编码识别算法并建立了电能质量扰动识别模型。算法对原始扰动进行降噪腐蚀处理，改善自编码模型泛化能力及扰动数据鲁棒性；对稀疏惩罚项和权重衰减项设限，能有效提升了识别模型应对海量、高维电能扰动数据的适应能力。多Logistic分类器组合进一步提高模型对原始不互斥扰动类型的匹配程度。仿真将验证整合算法的电能质量扰动识别模型的有效性，并与其它测试模型进行性能对比。

2 稀疏降噪自编码建模

2.1 网络建模

设某自编码模型具有三层网状结构，即输入层、隐藏层和输出层，存在编码、解码两映射关系。其计算公式为

h=f(x)=ωx+a

(1)

(2)

为使隐藏层表达出输入层的最佳特征，设置误差函数L(x，y)函数值最小为约束目标以优化自编码模型各参数。计算公式为

(3)

设有电能质量数据样本集S且x∈S，式(3)可简化为

(4)

式(4)以自编码模型输入、输出量为约束对象，忽略了自编码模型其它参数对特征量提取过程的影响。

2.2 特征提取强化

自编码模型在输入层到隐藏层的映射过程中，易出现将输入层神经元数据即电能质量扰动数据，直接复制给隐藏层神经元的现象[8]。对输入层扰动信号做降噪腐蚀处理，所获取信号更具鲁棒性且使自编码模型泛化能力增强。目前，腐蚀处理方法有以下两种[9]：一是为原始信号添加多维同性高斯白噪声，其计算公式如下

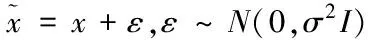
(5)

二是加入二进制掩蔽噪声，以概率P将原始信号中的数据置0，剩余数据保持不变。

若隐藏层神经元数量较多，则需增添隐藏层数以达降维目的。为减少层数且提升训练迭代速率，需向自编码模型加入稀疏性限制，解决方法是：通过在误差函数中增加稀疏惩罚项，使大多数隐藏层神经元处于未激活状态，凸显出携带信息的激活神经元，提高了模型提取原始数据抽象特征能力。稀疏惩罚项计算公式为

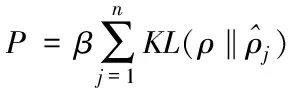
(6)

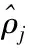
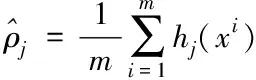
(7)

式(7)中，m为数据向量x的前一层神经元数目，式(6)中KL表达式可为

(8)

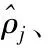
模型在训练过程中存在过拟合现象。为防止自编码模型在训练数据量充足的情况下，发生训练“过度”现象，通过添加权重衰减项加以限制[10]，其计算公式为

(9)

其中，λ为衰减项系数，nl为模型总层数，sl表示序号为l的某层神经元数目，ω为连接权重，约束目标为最小化R值。故稀疏降噪自编码所构成的新误差函数为

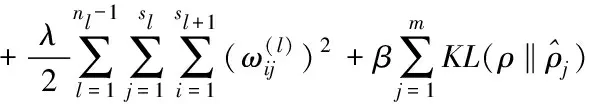
(10)

其网络结构如图1所示。

图1 稀疏降噪自编码网络结构

根据误差函数，采用梯度下降法对稀疏降噪自编码网络做微调优化；微调结束后，撤销稀疏降噪自编码输出层及其连接权重，保留剩余部分；特征提取完成后，需将抽象特征输入后续分类器加以训练。

3 Logistic分类器设计

Logistic分类器常用于二分类，当多类型识别对象之间不互斥有交集时，采用多Logistic分类器组合，性能稳定满足要求[11]。采用稀疏降噪自编码网络模型对电网扰动信号进行特征向量提取后，将隐藏层数据输入Logistic分类器中，计算公式如下

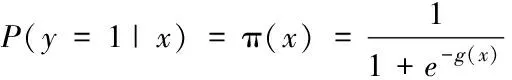
(11)

其中，g(x)=ω1x1+ω2x2+…+ωnxn。ωn表示序号为n的某权重，x为经过稀疏降噪自编码模型提取的特征向量。由式(11)得

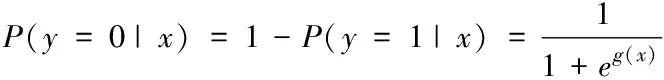
(12)

由于各输出类别互相独立，则联合分布为

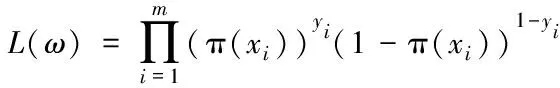
(13)

为降低运算复杂度，对式(13)取对数，获取的分类器输出似然函数为

(14)

其中θ为参数向量，有θ=(ω，a，b)。

后续求解J(θ)对各参数的偏导，采用梯度上升法对整个模型进行微调，能进一步优化整个网络模型分类性能指标。

4 算法流程设计

基于稀疏降噪自编码的电网电能质量扰动识别仿真算法流程如下：1)收集电网运行时常见的电能质量扰动类型，构建训练样本矩阵和测试样本矩阵；2)将所选训练样本进行归一化处理，并输入稀疏降噪自编码模型，初始化相关参数；3)采用梯度下降法对稀疏降噪自编码误差偏导函数做微调优化，强化特征提取；4)将抽象特征输入Logistic分类器，采用梯度上升法对分类器输出似然函数做优化迭代，提升模型性能；5)选定类别随机分布的测试样本，输入整合模型中，经过多次迭代，获取测试结果。6)获取可视化权重图、迭代均方误差及分类识别准确率。

5 仿真研究

5.1 信号生成

参考相关研究文献[12-14]构建电网常见的10种电能质量扰动信号。仿真信号参数设置如下：各类扰动信号基波频率为50Hz，采样频率为1000Hz，单个扰动信号在基频周期内被采样点数为68，采样时间为15个周期，共采样1024个点，对应稀疏降噪自编码模型输入的1024维度。

为验证本文所提算法的适用性，在仿真中通过控制变量设置合理步长，依次对各参数进行调整，最终生成各类扰动信号数据200组，共计2000组，其中1500组(各类型随机选取150组)数据用于训练稀疏降噪自编码网络模型，剩余500组用于测试。为了提高模型的收敛速度和运算精度，使用归一化方法将原始数据样本值集中在0至1之间，10种类型扰动信号经归一化处理后的波形图如图2所示，其中归一化公式为

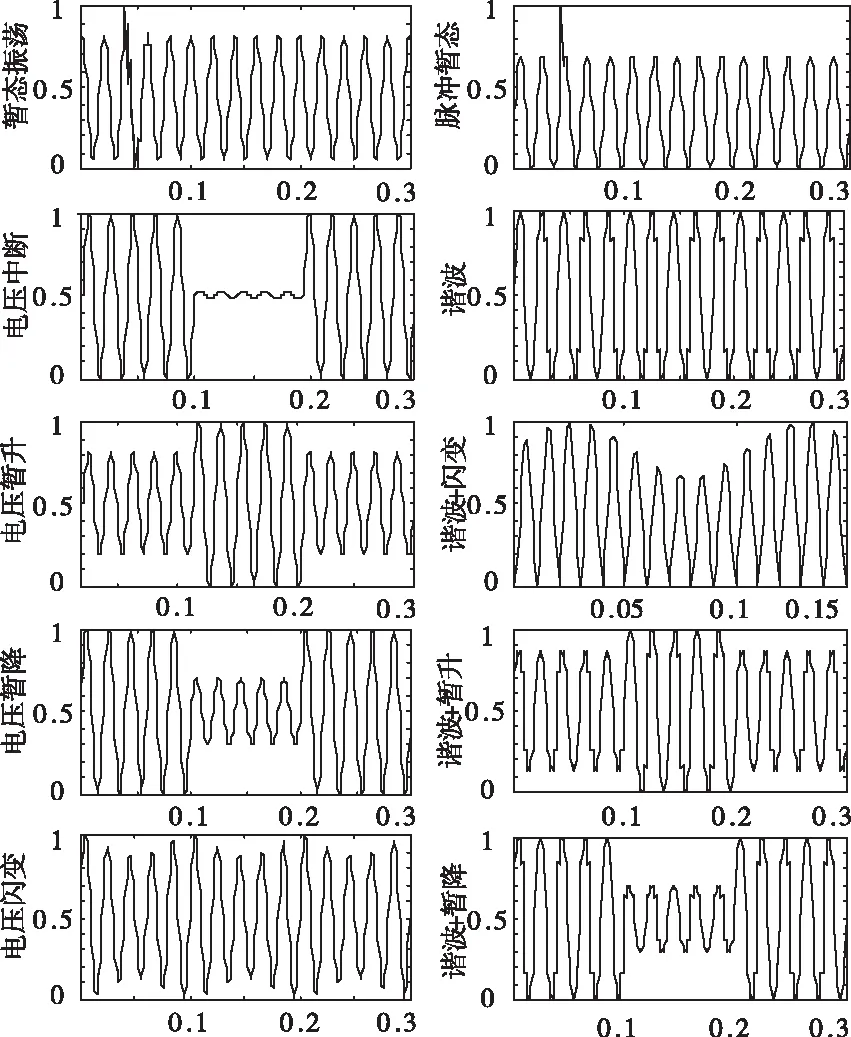
图2 归一化的10种扰动信号图

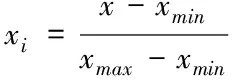
(15)

式中，xi表示归一化后的仿真数据值；x表示仿真数据值；xmin表示仿真数据中的最小值；xmax表示仿真数据中的最大值。

5.2 参数设置及实验结果

在网络模型训练过程中，多个舍弃输出层的自编码模型可以级联形成具有提取更深层次抽象特征的多隐藏层新自编码模型。增添了稀疏惩罚项以及经过降噪腐蚀处理后，自编码模型强化了特征提取能力，同时简化了模型结构。经过多次试运行得出，隐藏层数增多对提高模型识别率无益，采用单隐藏层即可达到仿真目的，且网络训练时间最少。

在Intel Core i7-4790(CPU主频为3.6GHz，内存8G)计算机上运行Matlab软件，四层基于稀疏降噪自编码的电能质量扰动分类网络模型参数设置如下：输入层神经元数目为1024，隐藏层神经元数量为200，输出层神经元个数为10，激活函数为sigmoid函数，稀疏参数ρ为0.05，学习率为0.5，掩蔽噪声系数为0.4，正向传递迭代训练次数为10，单批次数据量为100，反向微调迭代次数为70。仿真运行得出：平均分类识别率为99.8%。各类型扰动信号在不同噪声系数条件下的分类识别结果如表1所示。

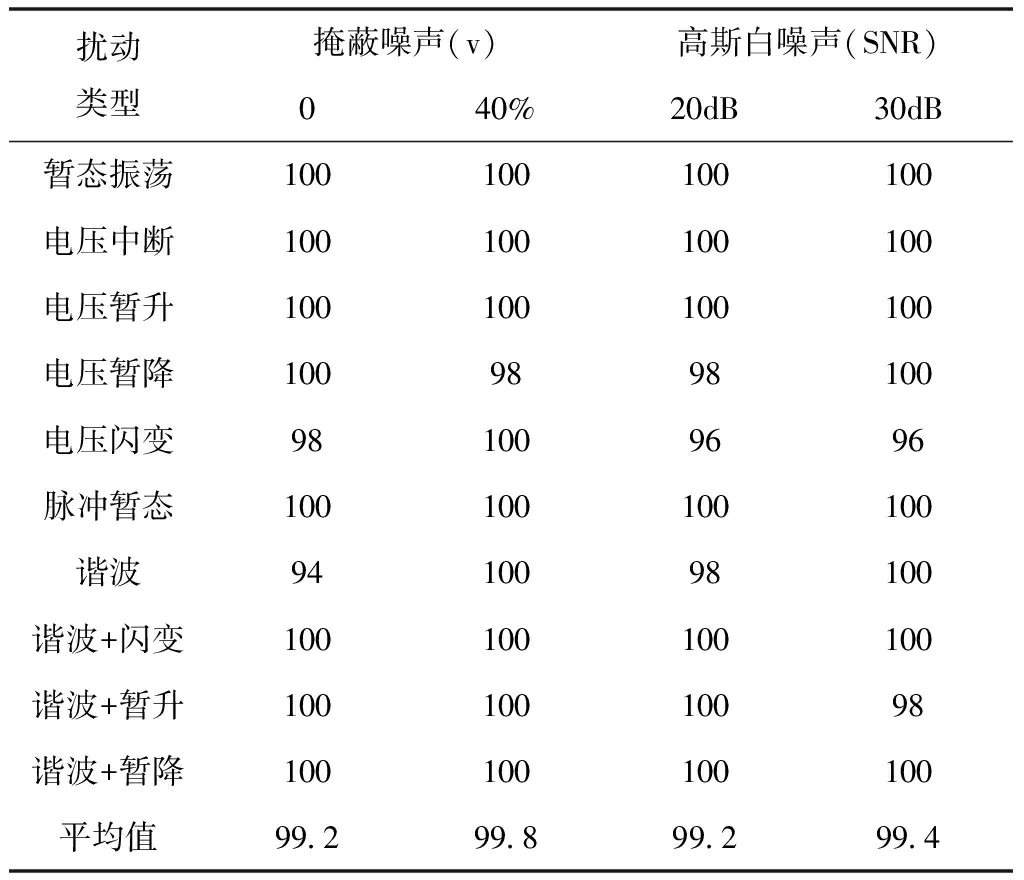
表1 各类型扰动在不同噪声系数下的分类识别率/%

表1中，当掩蔽噪声系数为0时，网络模型可视为稀疏自编码模型，平均识别率为99.2%；当掩蔽噪声系数为40%时，模型为稀疏降噪自编码模型，平均识别率为99.8%，表明具有降噪特性后，模型总识别率平均值得到提升。分别向原始仿真信号中添加高斯白噪声(SNR=20dB和SNR=30dB)后，模型分类识别率有所下降，但均维持在99%以上，表明所设计的稀疏降噪自编码模型对电能质量扰动识别处理有效且具有抗噪特性。

5.3 模型性能对比

为验证稀疏降噪自编码模型算法具有快速收敛性并推算识别准确率峰值时间，调整参数使模型呈稀疏自编码、降噪自编码、稀疏降噪自编码三种形式。以达到最高识别准确率所耗时长为标准，利用仿真的电能质量扰动数据进行迭代次数观测，结果如图3所示。

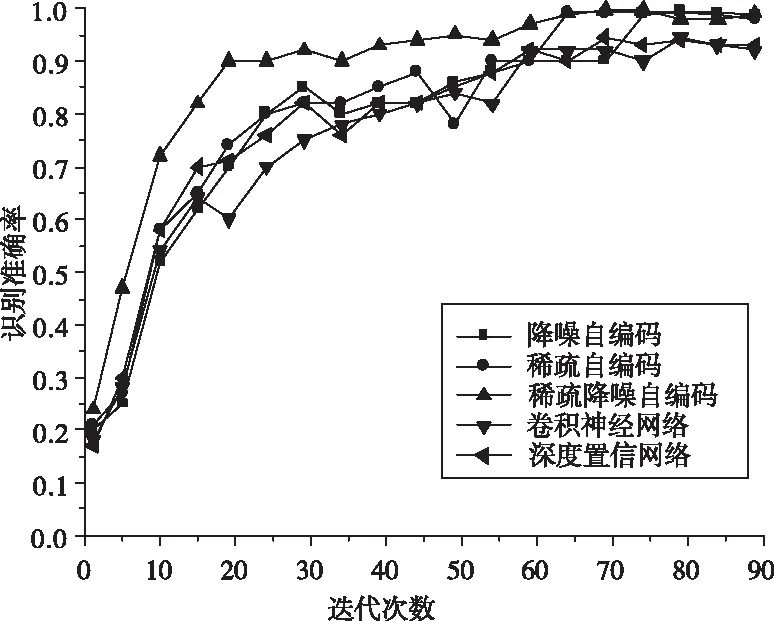
图3 不同模型训练迭代次数趋势

由图3可知，相较于稀疏自编码和降噪自编码，稀疏降噪自编码在迭代10次后，分类识别准确率开始处于领先水平，在20次时达到90.0%；随后在迭代70次时，达到最大值99.8%；而稀疏自编码和降噪自编码在前60次迭代时，两者相差不大，随后稀疏自编码凭借其提取原始特征的内在优势，在迭代65次时达到最高值99.2%；降噪自编码到达最大值所用时间最长，在迭代80次时获得最大准确率99.4%。将同样的电能质量扰动信号仿真数据导入文献[6]、[7]所提卷积神经网络、深度置信网络模型中进行等条件训练和识别测试，训练迭代次数趋势如图3所示，得到识别准确率最大值分别为94.6%、96.2%，明显低于本次设计的稀疏降噪自编码模型。融合吸收了稀疏自编码和降噪自编码长处的稀疏降噪自编码模型，弥补了卷积神经网络在抗噪性能，以及深度置信网络在累积误差方面存在的不足，模型整体性能获得提升。

为进一步分析稀疏降噪自编码模型对复杂扰动信号的分辨处理能力，分别使用单一扰动信号和复合扰动信号对模型进行网络误差重构测试，结果如图4所示。

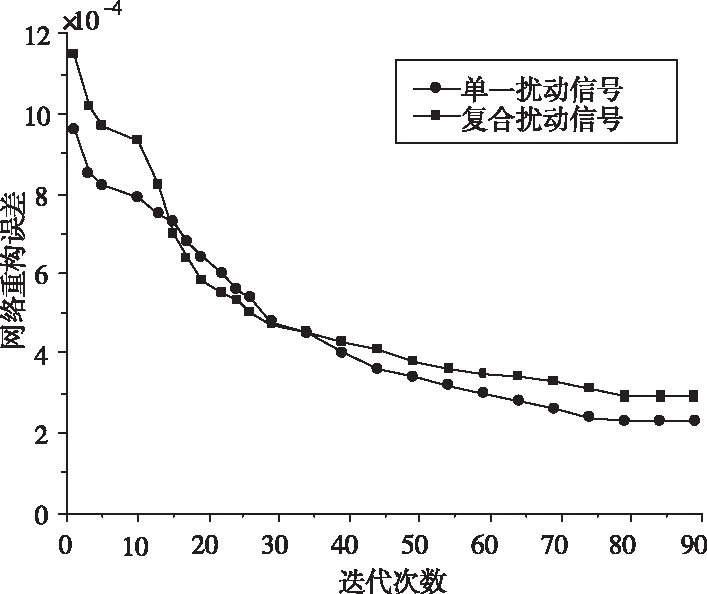
图4 扰动信号的网络重构误差

由图4可知在前13次迭代中，模型在识别复合扰动信号时的网络重构误差值大，但下降速度较单一扰动信号快，随后发生交替直至迭代30次左右再次发生交替。随着迭代次数增加，两种扰动网络重构误差变化趋于平缓，至迭代80次时达到平稳最小值。整个过程说明稀疏降噪自编码模型在面对单一、复合扰动信号时，最优迭代次数区间不同，当两者误差值趋于稳定时，复合扰动信号仍比单一扰动信号高，表明在同等条件下，稀疏降噪自编码模型对单一扰动信号的识别率高于复合扰动信号。

6 结论

对电网电能质量扰动信号进行识别研究，提取信号特征是关键步骤。本文采用稀疏降噪自编码算法对原始数据进行特征提取，其中稀疏惩罚项、权重衰减项及降噪腐蚀，分别在训练速率、数据拟合度、鲁棒性及模型泛化能力等维度，对自编码模型进行特征提取强化；反向微调模型参数后，消去了自编码模型输出层及其连接权重；选择与原始电能质量扰动信号匹配度相对较高的Logistic回归分类器，将隐藏层抽象特征作为输入进行模型整合并再次反向微调，识别性能进一步获得提升。仿真结果表明，所建分类识别模型，对影响电网电能质量的10种扰动信号(单一扰动信号7种和复合扰动信号3种)，均具有较高识别率和较强抗噪性，其中扰动识别平均准确率为99.8%；信噪比分别为20dB、30dB高斯白噪声环境下的识别率达99%以上。在达到相近识别准确率时，所建模型相较于其它识别编码形式在迭代次数(运行耗时)方面表现最佳。在面对单一、复合扰动信号混合时，所建模型对单一扰动信号的识别准确率略高于复合扰动信号。