加筋短板后屈曲特性分析与试验研究

刘 存

(航空工业第一飞机设计研究院，陕西 西安 710089)

1 引言

加筋板以其高比强度和高结构效率成为飞机结构的基本元素，被应用于机翼盒段、机身和尾翼盒段等主承力结构。在飞机服役过程中，加筋板经常受到轴向压缩载荷，屈曲后的极限承载能力是飞机设计所关注的重点。为充分发挥结构的承载能力，加筋板允许按后屈曲进行设计。对于飞机结构强度设计人员而言，如何准确预测加筋板在压缩载荷条件下的后屈曲响应及失效模式，是值得深入探究的问题。

受压加筋平板的柱曲线依据其长细比不同分为以加筋短板局部失稳而破坏的短柱、以加筋板局部失稳和弯曲失稳混合形式破坏的中长柱、以弹性弯曲失稳破坏的长柱[1]。国内学者对型材/长桁压损应力的进行了数值模拟、工程方法计算以及试验研究，给出了相关对比结果和结论[2-5]。而设计加筋板所使用的压损载荷/应力的计算需要满足以下前提：其一是筋条和蒙皮自由边是稳定的，即各元素均有较小的长细比。其二是稳定剖面不易发生局部屈曲且整个剖面能达到塑性屈服。未重视以上前提条件易造成蒙皮自由边过早失稳，得到的压损载荷非真实的压损载荷。而加筋短板在均匀压缩载荷作用下，蒙皮达到屈曲强度之前，蒙皮和筋条应力分配是均匀，随着载荷增加，处在筋条两侧的蒙皮发生屈曲，蒙皮不能承受比屈曲应力更大的应力，此蒙皮一边受筋条弹性支持，一边自由。蒙皮虽已失稳，但是筋条能承受更高的应力，直至破坏。国外学者对单长桁压缩进行了深入研究。Chiara Bisagni[6]使用代表多长桁壁板结构的单长桁压缩试验件，进行了有无分层的试验，用基于包含层间损伤壳单元有限元模型预测后屈曲响应以及损伤演化过程。Lynch[7]对压缩载荷下单长桁铆接加筋短板的后屈曲行为进行有限元模拟，并与试验和理论数据进行了比较，屈曲和破坏载荷与试验值误差在2.5%以内。AK.Patnailk[8]通过对比了铝合金7075-T6单长桁FSW板与传统铆接加筋板的压缩试验，得到了FSW板的初始屈曲载荷和破坏载荷均高于传统铆接板的结论。Bisagni C[9]采用帽型单长桁来研究加筋板数值模拟后屈曲响应，分析结果与试验吻合良好，且破坏模式一致。Vescovini[10]建立了快速参数化有限元模型来预测单长桁加筋板的后屈曲响应、失效模式以及损伤容限，并通过Global/local方法，用详细的局部模型扫描全局模型，以确定最关键位置的损伤容限。上述研究多使用有限元软件ABQUS进行了数值模拟，得到载荷-位移曲线，但均未求解其后屈曲平衡路径。

在上述研究的基础上，文中设计了加筋短板试验件，采用考虑加筋短板失效机理的工程计算方法得到了承载能力，进而采用GMNIA有限元仿真分析求解后屈曲平衡路径，并与试验进行了对比分析，得到了极限载荷及载荷-应变曲线。

2 加筋短板承载能力的工程计算

2.1 试验件设计

多长桁加筋壁板高昂的制造和试验成本限制了大规模的试验探索。为此，设计单长桁压缩试验件通过数值模拟用来研究后屈曲特性。试验件的总宽度为一个长桁间距150mm，根据试验件的长细比远小于20来设计试验件长度和剖面参数，试验件长度为100mm。试验件剖面如图1所示。具体剖面参数见表1。

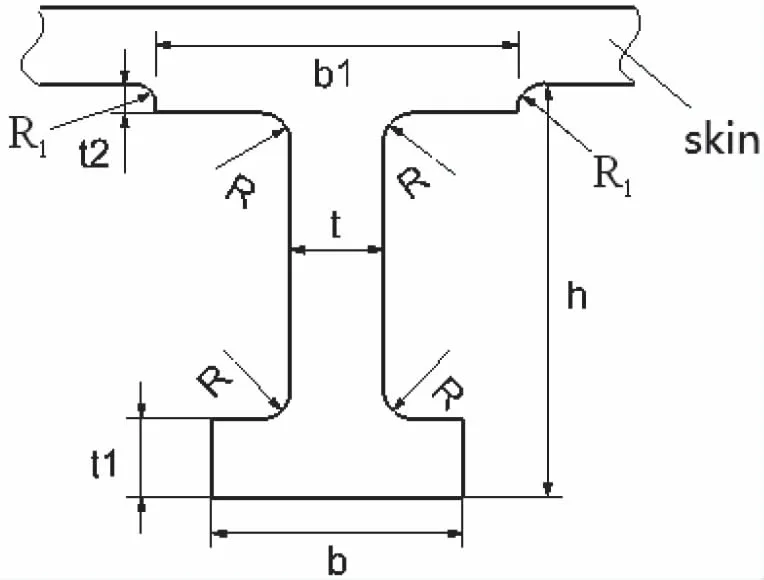
图1 试验件剖面简图

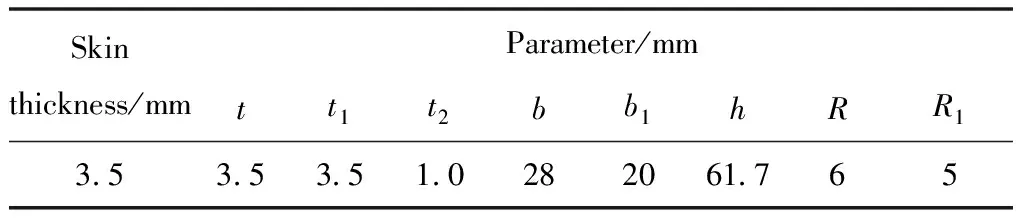
表1 剖面参数

试验件材料为毛料76.2mm的铝合金7150-T7751预拉伸厚板，材料性能参数[11]如下：压缩弹性模量Ec=73723MPa，破坏强度σb=565MPa，压缩屈服强度σ0.2c=530MPa。

2.2 承载能力的工程计算

半理论半经验的工程计算方法因其使用方便、计算简单而在航空领域广泛应用。对加筋短板的承载能力的计算通常采用“板元法”等工程分析方法，计算得到的加筋短板的承载能力与试验误差较大。文中在充分分析加筋短板失效模式和失效机理基础上，采用相对复杂的失效载荷计算公式[7]

Pult=A(str)σult(str)+A(eff)σult(sk)+(A(sk)-A(eff))σb(sk)

(1)

式中：Pult为失效载荷；A(str)为长桁剖面面积；σult(str)为长桁压损应力；A(eff)为蒙皮有效面积；σb(sk)为蒙皮屈曲应力；A(sk)为蒙皮剖面面积；σult(sk)为蒙皮压缩应力；

当薄壁剖面型材的长度较短时(长度与回转半径比L/ρ小于20)，剖面发生局部失稳后，型材还能承受较大的载荷，直到发生破坏(折皱、断裂)时，剖面的轴线仍保持直线。这种破坏形式被称为“压损”，其对应的破坏应力称为压损强度[12]。压损强度的计算公式如下

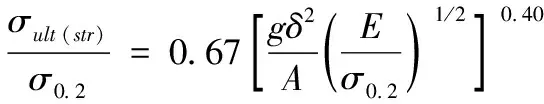
(2)

式中：σ0.2为屈服极限；A为加筋短板剖面面积；δ为蒙皮板厚度；E为弹性模量；g——切割数加凸缘数[1]，g选取为12.75；

蒙皮压缩应力采用Johnson-Euler方程[1]

(3)

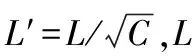
蒙皮的局部屈曲应力采用承受均匀轴向压缩载荷矩形平板弹性临界应力计算公式

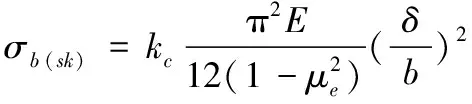
(4)

式中：b为加载边的宽度；kc为压缩临界应力系数，三边简支一边自由取3.65；μe为材料的弹性泊松比；

一边自由状态下蒙皮有效宽度计算[13]如下

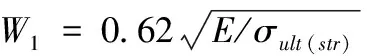
(5)

则蒙皮有效面积为A(eff)=δ×W1，通过以上式(1)～(5)可以计算得到加筋短板的承载能力为354.67kN。

3 有限元仿真与分析

3.1 有限元模型

试验件为整体加筋短板，为更好的模拟其后屈曲特性，采用可以考虑大变形和材料非线性的壳单元，长桁和蒙皮共节点。考虑到局部屈曲的发生，必须细化有限元模型，以便模拟其压缩屈曲波，每半个波至少采用5个节点。有限元模型网格划分如下：横剖面上蒙皮划分140个单元，长桁腹板划分60个单元，自由凸缘划分20个单元，单元均为壳单元CQUAD4。

为了便于载荷—位移数据的直观快速获取，在预测试验件极限承载能力时，采用类型为RBE2的多点约束单元模拟载荷的施加，加载点为主动节点，施加强迫位移载荷，约束三向XYZ位移。加筋短板端面为从动节点，约束蒙皮面外的Y向位移。有限元模型的加载和约束条件如图2(a)所示。为了使载荷均匀施加在加筋短板端面，以便更好的跟踪后屈曲平衡路径，采用Nastran卡片SPCD施加强迫位移试验机将载荷均匀施加在加筋短板加载端的端面上。有限元模型的加载和约束条件如图2(b)所示。加筋短板的约束端均约束三向XYZ位移。

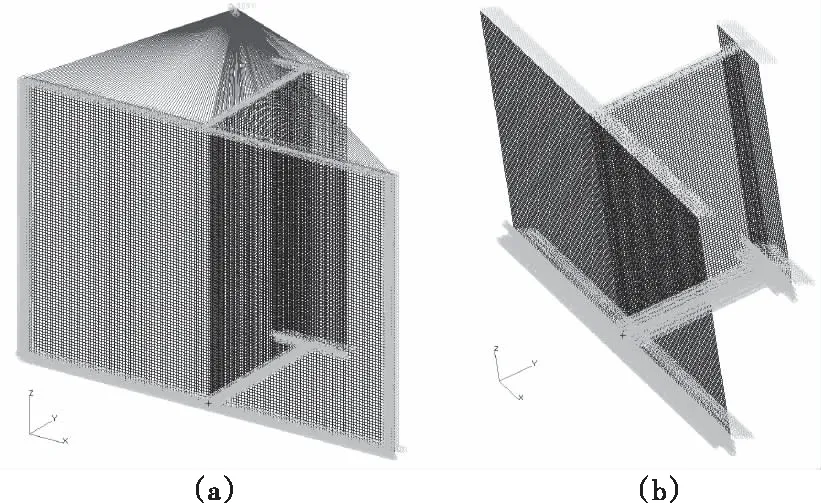
图2 有限元模型加载及约束图

加筋短板试验件材料非线性的定义如图3所示。首先在MSC.Patran中定义输入弹性变形参数，先将材料本构模型定义为弹性，再通过逐点输入非线性应力应变数据将该材料的本构模型定义为弹塑性。

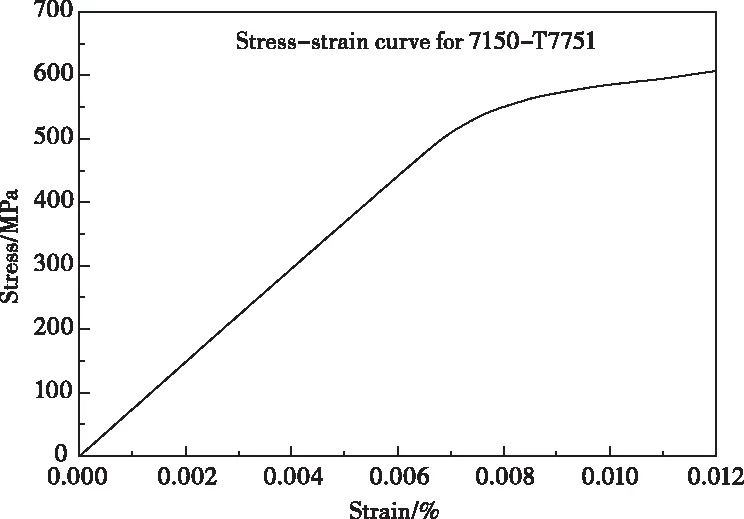
图3 7150-T7751板材应力—应变曲线

3.2 求解策略

制定求解策略的目的就是为了预测极限载荷和跟踪后屈曲加载路径。在纵向压缩载荷作用下加筋壁板典型屈曲特性如图4所示，屈曲后的加筋板刚度下降，在达到破坏载荷之前，加筋板进入后屈曲状态，进而失效或坍塌。从加筋板发生屈曲开始，屈曲模态的转换现象就可能发生，壁板的屈曲波形随载荷的增加而发生变化。

筋短板整个失稳过程中实际的载荷—位移关系，获取失稳前后的全部信息，首先基于有限元模型采用SOL105进行线性屈曲分析，获取结构的屈曲模态，其次将一阶屈曲模态乘以扰动系数，作为结构的初始缺陷，然后运用FILED将初始缺陷加入有限元模型。在此基础上采用基于Newton-Raphson迭代的弧长法(Arc-Length Method)进行非线性后屈曲计算[14]。

由于弧长法在失稳前后系统的非线性很强，需要足够小的载荷步长才能准确模拟失稳路径，因此需要足够多的增量步分析。加筋短板的有限元模型的位移载荷被分为90个等增量，采用ITER方法控制切线刚度修正，矩阵修正之前的迭代次数为500，每个载荷增量的总迭代限为2000。采用NLPCI卡定义非线性静态分析中弧长增量求解策略，弧长法类型为MRIKS，最小弧长比为0.05，最大弧长比为5.0，期望收敛的迭代次数为100，每步最大迭代次数1000。

3.3 承载能力预测

采用上述求解策略，对加筋短板有限元模型进行求解，求解时开启大变形(LGDISP)考虑几何非线性，引入材料的弹塑性本构关系，得到加筋短板的极限承载能力为368.3kN。提取载荷及位移的计算结果，绘制的载荷-位移曲线如图5所示。

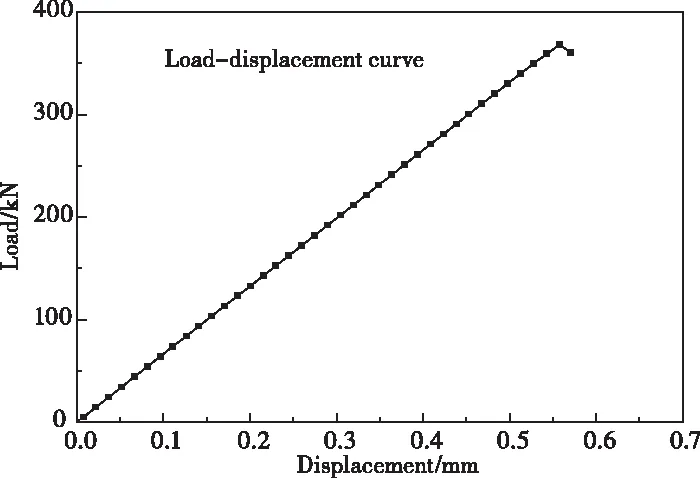
图5 加筋短板加载端载荷—位移曲线图

4 试验

4.1 试验概述

加筋短板试验件在型号为YAM-2000F(5000)结构稳定试验机上进行试验，试验时确保试验件的形心与试验机压盘的圆心共线，以保证试验件均匀受压。通过布置的应变片检查加筋短板的对中性以及同一截面上应变值的均匀性，直至达到试验要求。为了对试验过程实施监控及监测，在加筋短板蒙皮和长桁的关键部位布置应变片，应变片均布置在试验件的长度的1/2处，应变片布置剖面图如图6所示，共12个测量点，长桁蒙皮均布置单片，应变片方向沿试验件长度方向。

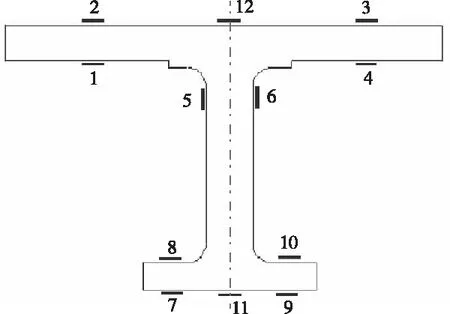
图6 试验件应变片布置图

4.2 试验结果

加筋短板试验件在屈曲前的线性区域剖面应力均匀分布，蒙皮能够均匀的承受压缩载荷。随着载荷的增加蒙皮开始出现屈曲，进入非线性后屈曲区域，载荷继续增加，长桁与有效宽度内的蒙皮继续承受，当达到其极限承载能力时，载荷达到峰值，此后，加筋短板进入后坍塌区域。加筋短板试验件在连续加载过程中，均产生了明显的局部失稳现象，部分出现长桁与蒙皮的撕裂分离现象，即使没有声音产生，直到不能继续承载，也视为破坏。5件试验件的破坏载荷及其平均值见表2。

表2 破坏载荷试验结果

可见，试验值与本文的工程计算方法相对误差4.14%，基本满足工程应用需求。

5 有限元仿真与试验对比分析

5.1 极限载荷对比

由加筋短板加载端载荷-位移曲线可见，曲线在初始阶段呈线性，加载到368.3kN时，曲线达到顶点，曲线斜率由正值变为负值，即为结构的极限载荷。随后，位移继续增加，载荷下降，结构丧失承载能力。有限元仿真得到的极限载荷为368.3kN，试验破坏载荷的平均值为370.0kN，两者的相对误差为0.46%，表明有限元仿真分析可以准确的获取加筋短板压缩极限载荷。

5.2 破坏模式对比

一步分析加筋短板的破坏模式可知，蒙皮边缘的变形较大且一侧蒙皮突起而另一侧蒙皮凹陷，两者组成一个完整的屈曲波；长桁腹板有明显的屈曲变形并朝一侧弯曲。从整个破坏过程来看，长桁剖面发生局部失稳，压缩载荷继续增加，增加部分由较刚硬的角区承受，直到应力增加到足够的数值造成破坏。而从蒙皮和长桁腹板的失稳先后次序来看，蒙皮先失稳。有限元模拟破坏时刻位移云图如图7所示，试验件典型破坏形貌如图8所示。可见，有限元仿真与试验的破坏模式一致。

图7 FEA仿真破坏时刻变形云图

图8 试验破坏形貌

5.3 载荷-应变曲线对比

加筋短板试验件处于纯压缩状态，背对背的应变片1#和2#位于一侧蒙皮中心点上，背对背的应变片3#和4#位于另一侧蒙皮中心点上，且均在试验件长度1/2截面上。1#和2#应变片以及3#和4#应变片的应变随加载步变化曲线的有限元仿真值与试验值的对比如图9所示，FEM为有限元仿真压缩方向的应变。试验件形心处长桁腹板两侧背对背的应变片5#和6#随加载步变化曲线的有限元仿真值与试验值的对比如图10所示。其中有限元仿真曲线从Nastran计算结果文件t16中的layer1和layer5中获取，分别对应试验件背对背的应变片。

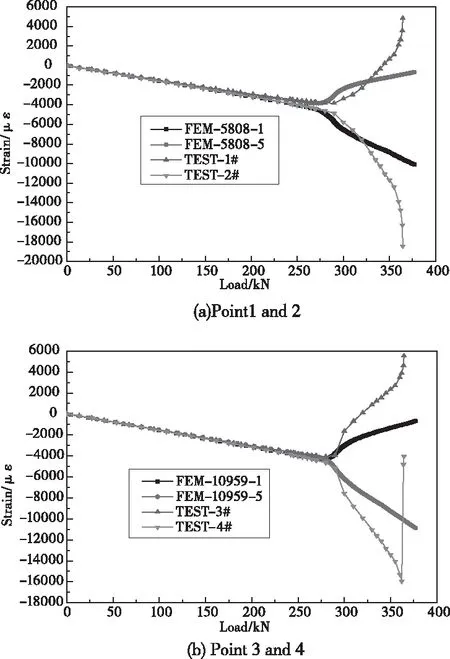
图9 加筋短板蒙皮中心有限元与试验载荷—应变曲线对比

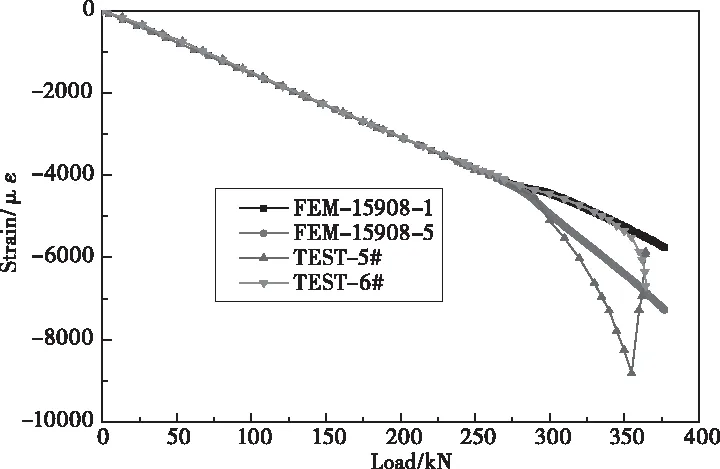
图10 加筋短板形心有限元与试验载荷—应变曲线对比

从图9可见，试验件中心点的蒙皮处(应变片1#、2#)的载荷-应变曲线均在起始阶段呈现线性变化，在载荷增加到270kN左右时，试验与有限元模拟载荷-应变曲线均出现了明显的拐折，据此推断该处产生了较大的面外位移，即发生了局部屈曲。其中，屈曲点的判断为背对背的应变平均值随载荷变化曲线斜率发生明显变化。图10所示的加筋短板形心处有限元仿真与试验载荷—应变对比曲线的屈曲载荷为300kN，与蒙皮中心点相比，载荷明显较高，说明屈曲发生较晚，这与形心处长桁边界支持刚度较强有关。图9、图10显示的有限元仿真和试验实测曲线在线性段吻合良好，结构发生屈曲后，有限元仿真分析和试验实测曲线变化趋势基本一致，但仍存在一些偏差。可见，要更加准确求解加筋短板压缩的后屈曲路径需要考虑更多的影响因素，这也为有限元仿真分析提出了更高的要求。

6 结论

通过对加筋短板压缩试验件的仿真分析，预测了结构的承载能力，得到的破坏模式与试验一致，典型部位的载荷-应变曲线与试验数据吻合，达到了采用NASTRAN预测加筋短板极限载荷和跟踪后屈曲平衡路径的目的。得到以下结论：

1)采用考虑加筋短板失效机理的工程计算方法，与试验的相对误差小于5%，基本满足工程设计要求；

2)采用GMNIA有限元仿真分析方法预测的极限载荷，与试验的相对误差在1%以内；

3)基于NASTRAN的有限元仿真能够较好的跟踪后屈曲平衡路径以及准确的预测结构承载能力、破坏模式，对非线性后屈曲区域和后屈曲坍塌区域的深入的研究提供技术支持；

4)基于NASTRAN的有限元后屈曲分析能很好预测加筋短板的后屈曲特性，可作为加筋短板强度设计和强度预报的一种有效分析手段。