四旋翼吊挂变质量负载建模与控制方案设计

郗厚印，张 栋，杨云霄，周 涛

(青岛理工大学信息与控制工程学院，山东 青岛266520)

1 引言

四旋翼与传统无人机相比，结构简单、可垂直升降和悬停，被广泛应用于物流配送、农业生产、城市监控和无线通讯等领域[1-3]。在这些应用中，一般四旋翼会吊挂负载实现运输与作业功能。但由于负载的可变性和飞行器自身稳定性的限制，目前这些应用大多数正处于试用阶段。因此，设计稳定可靠的四旋翼吊挂运输系统具有重要的意义。

与将负载固定在机身上相比，采用吊挂的方式不需要考虑负载与机身外形的匹配以及负载体积问题，不会对姿态角的响应速度产生较大的影响。但采用吊挂的方式会增加系统数学模型的复杂度，再加上四旋翼本身的欠驱动、强耦合特性和不可避免的外界干扰，使得原本复杂的四旋翼动力学模型更加难以建立，对控制器设计也提出更多挑战[4，5]。

建立合适的四旋翼吊挂变质量负载系统的数学模型是实现良好控制效果的前提。目前，在四旋翼吊挂负载系统模型的研究上，普遍存在的问题是模型过于复杂或者简化后不能完全表征系统特性[6，7]。在数学模型得到一定程度解决的基础上，为了提高四旋翼吊挂负载系统的飞行性能，研究者们提出了各种不同类型的控制策略。文献[8]基于能量法设计了一种非线性控制策略实现了对无人机位置的精确控制和飞行过程中负载摆动的快速抑制。文献[9]利用几何控制和微分平滑的方法来控制四旋翼吊挂负载系统。文献[10]在简化四旋翼吊挂系统模型的基础上采用二型模糊防摆控制，取得较好的控制效果。但上述研究所设计的控制器均未考虑吊挂负载质量变化对控制性能的影响。文献[11]研究了四旋翼负载质量变化情况下的稳定控制，采用分层的非线性控制策略，虽然在外界干扰情况下能实现稳定控制，但未考虑负载质量突变的情况。文献[12]采用鲁棒滑模控制器实现吊挂变质量负载四旋翼高度的稳定控制，但建模时未考虑负载对系统动力学的影响。

针对上述问题，本文基于牛顿-欧拉法建立此类无人机吊挂系统的数学模型，以便于理解且与实际应用相结合。考虑负载吊挂运输过程中质量渐变或突变以及外界扰动对四旋翼的影响，采用ESO对复合扰动进行实时估计和补偿，实现其水平位置控制；采用反步法设计姿态和高度控制器提高系统的稳定性与抗扰能力。与传统反步控制相比，能有效改善四旋翼在负载质量变化以及外部环境干扰下的机身抖动与漂移现象。

2 四旋翼吊挂变质量负载系统动力学模型

2.1 四旋翼吊挂负载系统结构与坐标系定义

四旋翼吊挂系统的结构图如图1所示。定义了描述六自由度刚体运动的两种参考坐标系：惯性坐标系{E}和机体坐标系{B}，{xe，ye，ze}及{xb，yb，zb}分别表示两个坐标系的正方向。在四旋翼初始时刻，惯性坐标系与机体坐标系姿态一致。

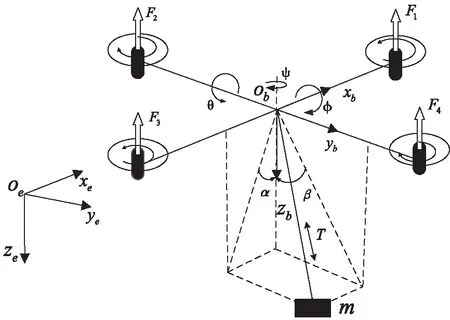
图1 四旋翼吊挂系统示意图与坐标系

根据四旋翼实际飞行情况作出以下假设：

1) 四旋翼机身视为均匀对称刚体，几何中心与质心重合。

2) 吊挂负载的绳子张紧，且长度不变，忽略绳子质量。负载始终在飞行器下方，吊挂点与四旋翼的质心重合。

定义四旋翼在{E}中的位置坐标为{x，y，z}，负载在{E}中的坐标为{xl，yl，zl}，Fi(i=1，2，3，4)

分别为四旋翼四个旋翼的产生的升力。{φ，θ，ψ}分别为四旋翼的滚转、俯仰和偏航角。M和m(t)分别为四旋翼和负载的质量，负载质量随时间改变。l表示绳长，T表示绳子的张力。α为绳索在xoz平面内的投影与竖直方向的夹角，β为绳索在yoz平面内的投影与竖直方向的夹角，方向满足右手定则。摆角α与β的零初始值是竖直向下，与z正方向重合。

2.2 四旋翼吊挂变质量负载系统牛顿-欧拉建模

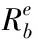
(1)

式(1)中，c(i)=cos(i)，s(i)=sin(i)。

对吊挂负载的四旋翼系统建立其动力学模型，U1表示由四个电机产生的总推力值。其在惯性坐标系中的分力为Ux，Uy，Uz，表示为

(2)

假定四旋翼初始位姿与惯性坐标系相同，四旋翼在{E}中的位置{x，y，z}与负载的位置{xl，yl，zl}满足如下关系

(3)

式中，Rot(β)和Rot(α)分别表示旋转矩阵，为

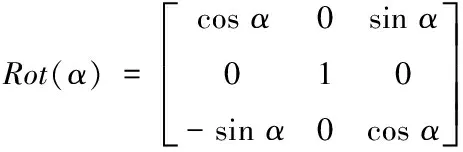
由式(3)可得，负载质心位置坐标用四旋翼位置坐标和绳子的摆角可表示如下

(4)

为得到四旋翼加速度与负载加速度之间的关系，对式(4)两边求二阶导数，可得

(5)

对四旋翼和悬挂负载运用牛顿第二定律得

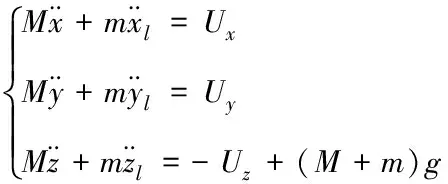
(6)

(7)

假设四旋翼的姿态角φ，θ，ψ在一定小范围内变化。并将变负载对四旋翼姿态的影响看作一个随时间变化的复合扰动。此外四旋翼姿态动力学还考虑因刚体旋转而产生的陀螺效应[13]。基于前面所作的假设，在机体坐标系内建立姿态动力学模型[14]如式(8)所示。

(8)

式(8)中，dφ，dθ，dψ表示模型中的复合干扰，包括由变质量负载产生的扰动及外部环境扰动。Ix，Iy，Iz表示四旋翼各个轴的转动惯量。Jr表示电机转子和桨叶绕轴转动的总转动惯量。L为电机轴心到四旋翼质心的距离。U2，U3，U4为控制输入，其与螺旋桨的转速有关[15]。Ωr=Ω1-Ω2+Ω3-Ω4，Ωi，(i=1，2，3，4)为各个电机的转速。

式(7)和(8)组成四旋翼吊挂变质量负载的牛顿-欧拉动力学模型，该模型建模过程较拉格朗日-欧拉动力学模型建模过程简单，便于理解且与实际应用相结合。并且该模型体现了吊挂系统中四旋翼质心与负载质心的位置动力学以及摆角的变化。同时，将负载对四旋翼姿态的影响看作是干扰，以此简化模型的复杂度。另外，该模型考虑了负载质量的变化，用以分析变质量负载的相关问题与控制器设计。

3 四旋翼吊挂变质量负载系统控制器设计

结合四旋翼吊挂变质量负载牛顿-欧拉数学模型的特点，控制系统采用ESO和反步法相结合的串级控制方案，如图2所示。水平位置在ESO对负载产生的扰动进行实时估计和补偿的基础上，采用PD控制器实现对参考位置的跟踪。高度和姿态环采用反步控制器实现高度和姿态的稳定控制。

图2 四旋翼吊挂变质量负载系统控制方案

3.1 基于ESO的水平位置抗扰控制律设计

水平位置控制器设计中，针对变质量负载建模误差以及外界扰动组成的复合干扰，设计ESO对该复合干扰进行实时估计与补偿。

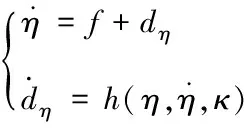
(9)

式(9)中，f表示四旋翼的水平位置动力学方程，dη为模型扩张出来的状态，表示系统的复合干扰。κ表示外界扰动。针对式(11)设计ESO为

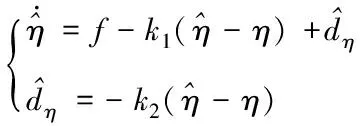
(10)

定义水平位置跟踪误差为ξe=ξd-ξ。设计水平位置抗扰PD控制器为

(11)

式(11)中，kp和kd为抗扰PD控制器参数。φd和θd分别为滚转角和俯仰角的期望值。

3.2 基于反步法的姿态和高度控制律设计

反步法是一种针对不确定系统的系统化控制方法，将李雅普诺夫函数的选取与控制器相结合的一种回归设计方法[17]。

在考虑干扰的情况下，四旋翼高度与姿态非线性动力学模型可以写为

(12)

式(12)中，X=[x1x2x3x4]T=[φθψz]T，γ=[γ1γ2γ3γ4]T与g=[g1g2g3g4]T为非线性函数，U=[U2U3U4U1]T，dX=[dzdφdθdψ]T为扰动项。

姿态环控制器设计以滚转通道为例。

滚转通道的运动学可以写为

(13)

定义滚转角误差

e1=x1d-x1

(14)

式中，x1d为滚转角参考信号，对e1求导为：

(15)

选取李雅普诺夫函数为

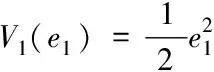
(16)

对时间求导得

(17)

(18)

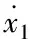
(19)

式(19)中，取c1为一个正常数。

定义第二个误差函数为

(20)

式(20)对时间求导为

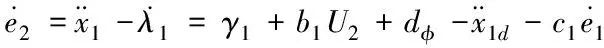
(21)

选取李雅普诺夫函数为

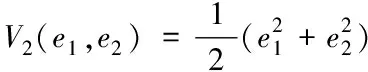
(22)

对时间求导得

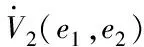
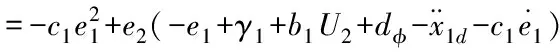
(23)

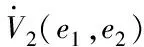
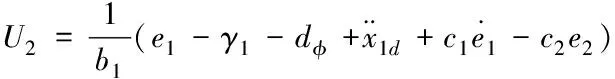
(24)

式(24)中，取c2为一个正常数。将方程(24)代入式(23)可得

(25)

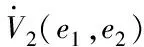
同样方法，可以得到俯仰，偏航的控制律U3和U4，并证明其控制子系统也是渐近稳定的。

高度运动学方程可以写为

(26)

e7=x4d-x4

(27)

式(27)中，x4d为高度参考信号。求导得

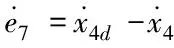
(28)

选取李雅普诺夫函数为

(29)

对时间求导得

(30)

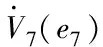
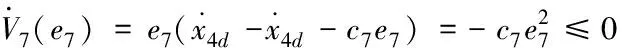
(31)

式(31)中，取c7为正常数。

定义另一个误差函数

(32)

式(31)可以写成

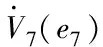
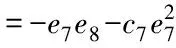
(33)

定义一个新的李雅普诺夫函数

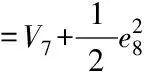
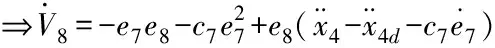
(34)

(35)

式中，取c8为正常数。

为满足上述关系，令式(35)两边相等，可得高度控制子系统的控制律为

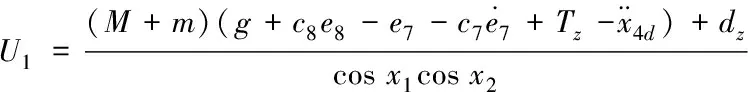
(36)

4 仿真与分析

在MATLAB/SIMULINK环境下，基于本文所建立的四旋翼吊挂变质量负载模型及其抗扰串级控制回路进行仿真，并与传统PID控制器串级控制进行比较，以验证在存在负载质量变化及外部干扰情况下，四旋翼控制系统的轨迹跟踪能力和鲁棒性。仿真中，空载下四旋翼的物理模型参数如表1所示。

表1 四旋翼模型参数

在仿真中，给四旋翼无人机引入干扰(实际对应风扰等)，如图3所示，直至仿真结束。在运载货物，灾区救援等任务时，载荷可能需要围绕目标区域进行螺旋上升的运动，从而进行勘探或喷洒等任务。针对这种应用场景，设计一种三维螺旋上升曲线作为四旋翼的轨迹参考信号。参考信号方程为

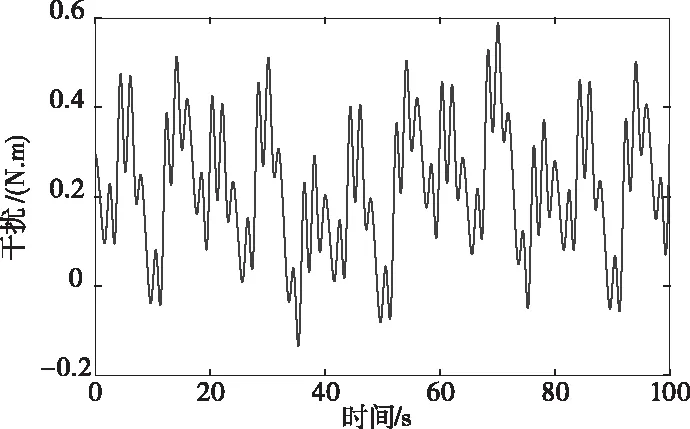
图3 仿真干扰

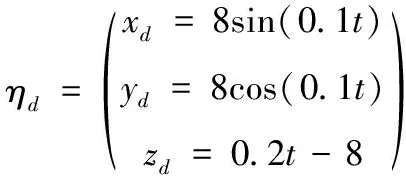
(37)

为了模拟负载变化带来的不确定性，设定负载的变化如图4所示。在5秒时接入负载，60秒后负载质量呈指数下降。负载质量变化方程为

图4 负载质量变化曲线

(38)

图5和图6分别给出位置以及姿态的对比仿真结果。从图5可以看出，四旋翼做螺旋式上升运动。由于外部干扰和负载质量突变，四旋翼的轨迹会偏离期望轨迹，但文本设计的控制策略相对传统串级PID控制器的跟踪误差小，所设计的控制策略能够有效解决吊挂变质量负载的四旋翼在有干扰情况下的轨迹跟踪问题。图6为姿态角的对比仿真结果，采用反步法设计的控制器得到的姿态角输出具有较小的稳态误差和较快的收敛速度，姿态角变化幅度比较小，且变化较为平缓，机身抖动较弱。

图5 轨迹变化对比曲线图

图6 姿态角变化对比曲线图

整体上看，将ESO与反步控制相结合应用于四旋翼吊挂变质量负载控制，能够更好地抑制由负载变化和外部环境产生的影响。与传统反步控制相比，既保证了传统反步控制对设定轨迹的精确跟踪，又能改善四旋翼飞行器吊挂负载在干扰环境中的机身抖动和漂移现象。较传统串级PID控制的抗干扰能力强，且具有较强的鲁棒性。图7展示负载摆角分别在xeoeze与yeoeze平面的分量。由仿真得四旋翼在负载质量突变后采用串级PID控制器时对应的负载平均摆角分量α和β分别为3.4度和3.9度，本文所设计的控制方案中四旋翼吊挂负载的平均摆角分量分别为1.7度和3.1度，且30秒之后的变化幅度明显小于串级PID控制器的对应控制摆角。

图7 α、β角的摆动对比

5 结论

针对四旋翼无人机吊挂负载执行任务时，负载质量变化和环境干扰影响飞行性能的问题，首先建立了四旋翼吊挂变质量负载的牛顿-欧拉动力学模型，并在该模型基础上设计了一种基于扩展状态观测器(ESO)和反步法相结合具有内外环结构的控制方案。

水平位置采用PD控制器，利用ESO对负载的扰动进行实时估计，并在控制律中进行补偿，不仅避免了控制过程中的复杂计算，且提高了系统的抗干扰能力。将变质量负载对姿态的影响看作外部干扰，根据系统严格反馈的特点，采用反步法进行四旋翼高度和姿态控制器的设计。仿真结果表明，该控制方案与传统串级PID控制器相比，具有较小的稳态误差和较快的收敛速度，稳定性与抗扰性较强。本文所提出的控制方案为四旋翼仓库吊运提供了理论研究和实际应用上的参考。