全尺寸无缝声衬静声联合载荷仿真分析研究
2022-03-01薛东文
杭 超,王 晨,薛东文,徐 健
(中国飞机强度研究所,陕西 西安 710065)
1 引言
飞机的噪声水平已成为影响其市场竞争力的重要技术指标。发动机是飞机最主要的噪声源,随着民用飞机对低耗油率等指标要求的提高,使得发动机涵道比越来越大,这种趋势使发动机风扇噪声在飞机噪声中的比重进一步增大。在发动机短舱中加装声衬是一种降低风扇噪声的有效手段[1,2]。近年来随着短舱降噪技术的革新,发展了无缝声衬技术。无缝声衬相比于早期的轴向接缝声衬,能够吸收高频段的宽频噪声而不是单一的处于叶片通过频率处的谐波噪声,具有更优的消声效果。典型的声衬结构由穿孔面板、蜂窝芯以及刚性背板构成。蜂窝芯的上下端面分别与穿孔面板和刚性背板连接,使蜂窝芯腔体密封且互相隔离,形成了多个独立的共振器,共振器的阻值是面板结构的函数,而其抗值是芯腔深度的函数[3]。
发动机短舱声衬结构在工作状态下,同时承受静压力载荷与声载荷激励,其中静压力载荷主要由声衬内外表面的压力差引起,声载荷主要由压气机/风扇产生的高强脉动音频冲击产生。声衬结构在以上静声联合载荷作用下可能出现疲劳问题。因此,有必要对声衬结构进行静载-声载联合仿真分析,评估声衬结构的强度,并根据仿真分析结果,为声衬结构抗静声联合疲劳设计提供参考[4]。有限元方法[5]、理论解析方法[6,7]和统计能量法[8,9]是分析结构声振响应的常用方法。
目前对声衬强度的研究主要集中在小型平板结构,缺少对全尺寸环形声衬结构的整体建模分析。而且在载荷形式上,仅考虑了单独的静载荷或声载荷,没有将两种载荷联合分析。本文提出基于旋转对称边界和对称边界的全尺寸声衬模型简化方法,克服了全尺寸声衬网格数量巨大的困难,对声衬结构同时施加静载和声载进行分析,仿真结果可以为声衬结构强度的设计提供参考。
2 声衬结构模型简化方法
声衬主要由穿孔面板、蜂窝芯以及刚性背板构成,其结构比较复杂,给结构强度分析带来诸多困难。尤其是全尺寸的短舱声衬结构尺寸非常大,且内部的蜂窝结构、穿孔面板局部尺寸复杂,想要直接对全尺寸的环形无缝声衬进行强度分析几乎是不可能完成的。因此,需要针对无缝声衬的结构特点,通过旋转对称边界条件与对称边界条件对其结构进行简化,减少网格数量,便于进行强度分析。
短舱声衬结构近似可看作薄壁柱面结构,它的几何形状沿轴向和周向都具有对称性,两个圆形端面的边界条件接近固支边界条件,且受到的静载和声载均垂直于圆柱表面。由此可知,声衬结构关于其轴向中面几何形状对称、边界条件对称、载荷对称,因此可以在声衬轴向中面处,通过对称边界条件对声衬结构进行简化,对称边界将结构简化成原结构的一半。同时,声衬结构关于中轴线具有旋转对称性质,可以采用旋转对称边界条件对其结构进行简化,旋转对称边界条件将圆柱面看作由多个扇形柱面组成,由其中一个扇形柱面代表整个圆柱面,相邻扇形柱面的场值相差一个相位因子。声衬结构的模型简化方法如图1所示。

图1 声衬结构的模型简化方法
3 模型简化方法验证
为了验证上述模型简化方法的正确性,本节通过简单算例对上述旋转对称边界条件与对称边界条件的简化方法进行分析,证明简化结构与全尺寸结构的等价性,同时证明了边界条件设置的合理性。
3.1 算例仿真参数
以圆筒结构为分析对象,几何尺寸如下:直径400mm,长度200mm,壁厚2mm。对圆筒结构建立两种模型,一种为全尺寸模型,另一种为经旋转对称边界条件与对称边界条件简化的模型,简化模型对应的圆心角为18°,长度为100mm,是全尺寸结构长度的一半,简化模型的几何大小为全尺寸模型的1/40。圆筒全尺寸模型和简化模型如图2所示。选取圆筒材料为钢,其密度为7800 kg/m3,弹性模量为210 GPa,泊松比取0.3。全尺寸模型和简化模型都受到垂直于表面向外的均布压强,大小为0.1MPa。全尺寸模型的两边均为固支边界条件,简化模型在长度方向一边为固支边界条件,另一边为对称边界条件,沿周向的两边均为旋转对称边界条件,如图2所示。
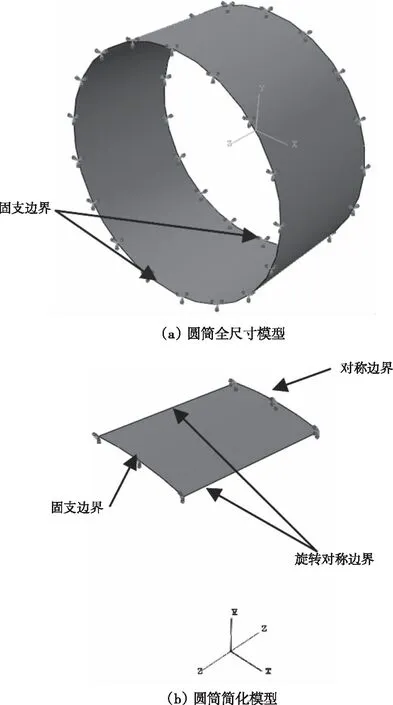
图2 圆筒有限元模型
3.2 算例仿真结果
圆筒全尺寸模型和简化模型在静压力作用下的变形分布分别如图3和图4所示。对比图3和图4可以发现,圆筒全尺寸模型和简化模型在受到静力作用后的变形分布相同,最大变形量均为9.199e-6 m。验证了简化模型在静力分析中的正确性。

图3 圆筒全尺寸模型受静载变形场

图4 圆筒简化模型受静载变形场
圆筒全尺寸模型和简化模型受到静压力作用后,对其分别进行模态分析。表1给出了全尺寸模型和简化模型的前10阶固有频率,通过对比可知,两种模型的固有频率基本相同,最大误差不超过0.03%,说明这两种模型计算出的固有频率一致性很好。
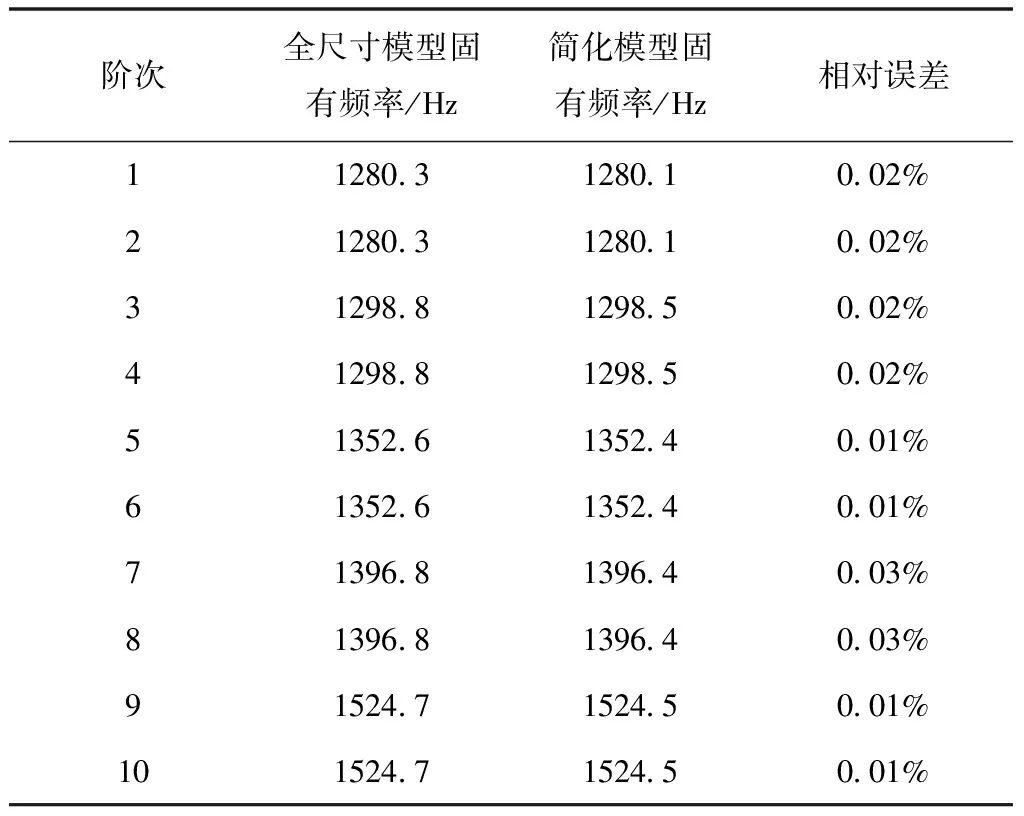
表1 两种圆筒模型的固有频率
接下来对两种模型的模态振型进行对比,受篇幅限制,仅给出模型前3阶振型。图5~图7给出圆筒全尺寸模型和简化模型的前3阶模态振型图。为了显示直观,将简化模型中的旋转对称结构全部显示出来。由振型图可知,两种模型的前3阶振型基本相同,依次为一阶七节径振型、一阶七节径振型(重根模态)、一阶八节径振型。说明这两种模型计算出的模态振型一致性很好。

图5 圆筒全尺寸模型(左)和简化模型(右)的第1阶振型

图6 圆筒全尺寸模型(左)和简化模型(右)的第2阶振型

图7 圆筒全尺寸模型(左)和简化模型(右)的第3阶振型
经上述分析可知,圆筒的简化模型能够很好的反映圆筒全尺寸模型的静态和动态力学特性,简化模型经旋转对称边界条件与对称边界条件简化,将环形结构几何模型极大地缩减,提高了仿真分析效率,且结果可靠性高。在后续的全尺寸环形无缝声衬的静-声联合载荷分析中,同样采用了上述基于旋转对称边界条件与对称边界条件的模型简化方法。
4 全尺寸无缝声衬静-声联合载荷仿真分析
4.1 声衬模型参数
声衬由穿孔面板、蜂窝芯以及背板通过胶粘形成,图8给出了蜂窝结构示意图。本文选取全尺寸环形无缝声衬的典型结构作为研究对象,其局部几何尺寸如下:正六边形蜂窝芯边长5.5mm,芯体高度23mm。穿孔面板、背板的厚度均为1.2mm,带孔面板上的小孔直径为1.2mm,小孔的分布形式为等边三角形,等边三角形边长大小为7.36mm。考虑到该结构具有对称性,故建立18°圆心角对应的扇段进行分析,在扇段两个端面建立旋转对称边界条件,同时沿长度方向取其一半,在中面上建立对称边界条件。经对称简化后,扇形模型的内表面弧长为241mm,长度为全尺寸的一半。声衬简化模型的几何大小为全尺寸模型的1/40。
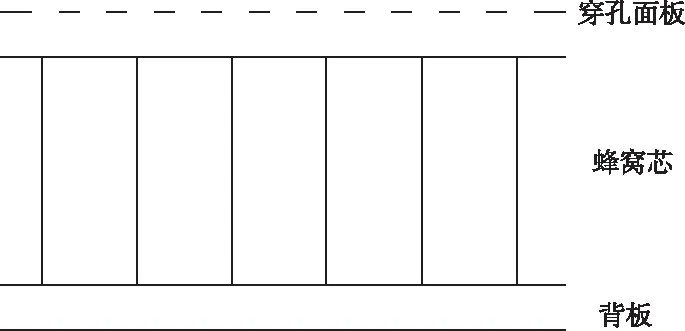
图8 蜂窝结构装配示意图
蜂窝芯材料为芳纶纸蜂窝,其密度为48 kg/m3,面内弹性模量为3.1 GPa,泊松比取0.2。带孔面板和无孔面板材料均为玻璃纤维/环氧树脂,其密度为2190 kg/m3,面内弹性模量为21 GPa,泊松比取0.16。声衬背板受都垂直于表面向外的均布压强,大小为0.1MPa,穿孔面板受到垂直于表面的声压载荷,载荷谱为宽频随机声载荷。声衬扇段模型的沿周向的两个端面为旋转对称边界条件,沿长度方向一边为固支边界条件,另一边为对称边界条件,蜂窝芯与穿孔板和背板之间为Tie约束。边界条件如图9所示。

图9 声衬扇段模型的边界条件
4.2 声衬静载响应分析结果
声衬在静压力作用下的应力分布如图10所示。由图可知,环形声衬在静载荷作用下最大应力位置位于穿孔板的固支边界处,最大应力为60.64MPa。声衬在静压力作用下的位移分布如图11所示,图中分别给出了单个声衬扇段与半个全尺寸声衬模型的位移分布图。由图可知,环形声衬在静载荷作用下最大位移位置位于背板的中间对称面上处,最大位移为1.23mm。

图10 声衬在静载作用下的应力分布

图11 声衬在静载作用下的位移分布
4.3 声衬静-声联合载荷响应分析结果
在对声衬进行声载荷分析之前,需要对声衬结构进行模态分析,此处的模态分析是建立在静载分析的基础上,考虑了静载对声衬结构模态参数的影响。模态分析结果表明,全尺寸声衬结构的前20阶模态频率分布在448Hz~708Hz之间,一阶固有频率为448.77Hz,对应的振型为一阶五节径振型。其中第19阶振型为声衬整体鼓包振型,对应的固有频率为677.09Hz。
静力分析和模态分析完成后,在环形声衬穿孔板表面施加声载荷谱,模态阻尼根据经验取0.02,根据模态叠加法计算声衬在每一个单频载荷作用下响应,声衬在宽频声载荷作用下的总体响应是所有单频激励下响应的叠加,本文中用单频载荷作用下响应代替宽频声载荷作用下的总体响应进行分析。
由声载荷分析结果可知,声衬在频率677.1Hz时(该频率是环形声衬整体鼓包振型对应的模态频率)出现最大应力,最大应力位置位于穿孔板中心对称面处,如图12所示,此时由声载荷引起的最大应力响应为1.33MPa。再从图7中读取该点在静载作用下的应力为47.43MPa。该点在静-声联合载荷作用下同时受到47.43MPa的恒定静载应力和1.33MPa的交变声载应力。

图12 声衬在声载荷作用下的应力云图(677.1Hz)
对声衬在声载荷作用下的每一个频率点的响应进行分析可以发现,所有声载荷激励频率引起的最大应力位置都在该点处,因此绘制该点的应力与激励频率的曲线,如图13所示。由图10可以看出,最大应力点在677.1Hz频率处的应力响应远高于其它频率,即使该频率处的声载荷幅值并不是最大(135dB)。图中第二个峰值对应的频率为1154.5Hz,在该频率下,声载荷的激励幅值最大(149.7dB),然而该频率并不处于声衬结构的固有频率,因此其响应不是很大。这说明环形声衬的整体鼓包模态对其声载荷响应影响很大。因此,在设计环形声衬结构时,应使声衬的整体鼓包频率避开声载荷幅值高的激励频率,避免出现共振放大现象。
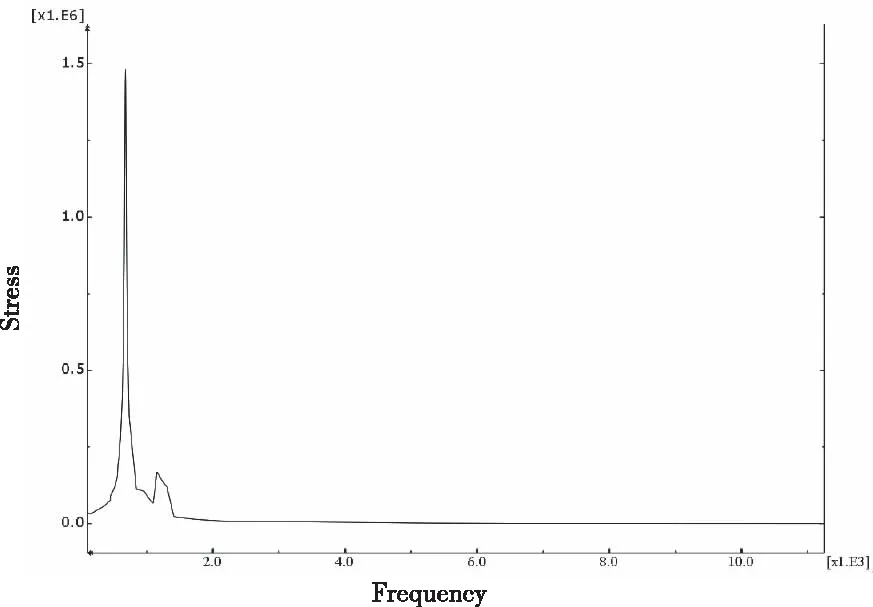
图13 声载引起的最大应力点的应力与激励频率的关系
5 结论
本文首先讨论了声衬结构有限元模型的简化方法,然后基于提出的简化方法建立了全尺寸环形声衬的简化有限元模型,最后对其进行了静力分析和声载荷分析。得到的主要结论如下:
a) 在环形结构的有限元分析中,基于旋转对称边界条件和对称边界条件的模型简化方法可以极大地减小结构的网格数量,且计算精度高。当简化模型的圆心角为18°时,简化模型的网格数量仅为原始模型的1/40,两种模型固有频率的最大误差不超过0.03%。
b) 全尺寸无缝声衬典型结构在静-声联合载荷作用下,其整体鼓包振型对其声载应力的影响最显著。声载引起的最大应力位置位于穿孔板中心对称面处,该点同时受到47.43MPa的恒定静载应力和1.33MPa的交变声载应力。
