航空器畅通和拥堵滑出时间计算方法

周 建，赵嶷飞，王同乐，姜文娟

(1. 中国民航大学空中交通管理学院，天津 300300；2. 北京首都国际机场股份有限公司公共区管理部，北京 100621)

1 引言

根据跑道和滑行道系统的拥堵情况，制定航空器在廊桥推出时机的智能控制策略，可以有效减少航空器在地面滑出等待时间、燃油消耗和碳排放，并缓解机场地面拥堵。而对航空器地面滑出时间进行精确计算是研究该策略的基础和前提。

航空器地面滑出时间根据机场地面拥堵情况可分为畅通滑出时间和拥堵滑出时间。FAA对畅通滑出时间的定义[1]为：在理想运行(不受机场地面拥堵和天气等延误因素的干扰)条件下，航空器从离开停机位到起飞离地过程的时间。拥堵滑出时间即为不畅通滑出时间。

国内外对航空器地面滑出时间的计算和预测已有研究。部分学者在构建数学模型时，仅选择地面滑出航空器数量为自变量。2002年，Idris等[2]首次选取地面起飞排队的航空器数量为自变量，用多元线性回归方法构建了航空器地面滑出时间数学模型；2010年，Balakrishna P等[3-5]选取有效交通数量(某航空器推出瞬间的地面滑出航空器数量与该航空器从推出至到达起飞等待队列过程中在廊桥推出的航空器数量之和)为自变量，建立了航空器滑出时间的数学模型；2010年，Jordan等[6]选取航空器的滑行距离和滑行速度为自变量，使用序列浮动前向选择方法构建了航空器滑出时间数学模型；2013年，Ioannis等[7]选取了起飞航空器调整数量为自变量，建立了航空器地面滑出时间数学模型。

另一部分学者在构建数学模型时，则将地面滑出航空器和滑入航空器数量选为自变量。2009年，Kistler等[8]选取了滑行距离、航空器停止数量、滑入和滑出航空器数量等参数为自变量，分别建立了线性和对数线性模型；2010年，Clewlow等[9]选取起飞排队航空器数量和落地滑入航空器数量作为自变量，建立了线性回归模型；2016年，赵嶷飞等[10]将起飞排队航空器数定义为针对某架航空器推出到起飞过程中其它起飞航空器数，将落地滑入航空器数定义为针对某架航空器推出到起飞过程中其它落地并进入机位航空器数，进一步提升了数学模型的拟合优度；2017年，瞿也丰等[11]构建航空器地面滑出时间模型时，将自变量地面航班数定义为在时间窗口内，已推出尚未起飞的航班数与已降落尚未进机位的航班数之和。

目前，国内外学者在建立航空器地面滑出时间数学模型时，部分学者对影响离港航空器滑出时间的关键因素认识不够，在自变量选取和定义方面存在不足；部分学者忽略了重型机和中型机开车(启动发动机的过程)时间的较大差异，未考虑机型影响因素；部分学者未具体说明对样本数据区间分段点的寻找方法，在计算方法方面存在不足，数学模型的预测误差率偏大。

本文首先对航空器滑出时间数学模型的自变量进行重新选取和定义，对离港航空器的机型进行了划分，然后用最小二乘法对样本数据进行分段，第一段样本数据用于航空器畅通滑出时间计算；第二段用于航空器在拥堵情况下滑出时间计算，最后用首都机场运行数据对数学模型进行检验。

2 研究对象

2.1 研究对象和变量选取

首都国际机场现有36L/18R、36R/18L和01/ 19共3条跑道。本文的研究对象为停靠在1号机坪，并使用36R跑道起飞的航班，如图1所示。

图1 北京首都国际机场平面图

从跑道资源被占用的角度，选取使用36R跑道起飞和落地的航空器数量为自变量，定义D为在某架离场航空器l从廊桥推出至起飞离地过程中，使用36R跑道起飞的航空器数量；定义A为在某架离场航空器l从廊桥推出至起飞离地过程中，使用36R跑道落地的航空器数量。

离场航空器l的地面滑出时间计算公式为

(1)

2.2 样本数据和筛选

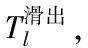
在统计过程中，对部分异常数据进行了剔除，主要原因包括更换跑道、复杂天气和航路限制等。

3 滑出时间计算

由于不同机型的推出开车时间不同，其地面滑出时间也存在差别，因此本文对停靠在1号机位区域的重型机和中型机的地面滑出时间分别进行了建模。

3.1 重型机

1)整体拟合

首先对重型机l重的统计数据进行初步整体拟合，建立多元线性回归方程如下：

(2)

式(2)中：D和A分别为离场航空器l重从廊桥推出至起飞离地过程中，使用36R跑道起飞和落地的航空器数量，架次。

2)分段拟合

众所周知，当D和A数值足够小的时候，航空器l重的滑出过程是畅通的，其滑行时间与D和A无关；当D和A数值较大的时候，航空器的滑出过程是拥堵的，其滑行时间与D和A相关。因此需要对样本数据进行分段拟合。

本文使用最小二乘法寻找样本数据区间的最优分段点。最小二乘法是一种数学优化技术，通过最小化待拟合数据的均方误差寻找数据的最佳函数匹配[12]。分别计算被不同分段点(D，A)分割的两部分样本数据拟合结果MSE之和，寻找其最小值，使全局最优，其对应的分段点即为最优分段点。

通过此方法计算得出最优分段点为(1，0)，则样本数据的前半段区间用于计算畅通情况下的滑出时间，后半段区间用于计算拥堵情况下的滑出时间。

3)畅通滑出时间

在样本数据统计过程中，记y重为重型机畅通滑出时间的发生频率，建立对数正态分布模型如下

y重=y0+c/(sqrt(2*PI)*σ*x)

*exp(-(lnx-μ)2/(2*σ2))

(3)

式(3)中：μ和σ分别为重型机畅通滑出时间对数的平均值和标准差，y0和c为常数。

使用正交距离回归算法对重型机样本数据进行回归分析，得到重型机畅通滑出时间频率分布的拟合函数如下

y重=0.03281+0.74071/(sqrt(2*PI)*0.1952*x)

*exp(-(lnx-6.91206)2/(2*0.19522))

(4)

对应的拟合曲线如图2所示。根据式(4)中的μ和σ值，计算对数正态分布模型的期望值为

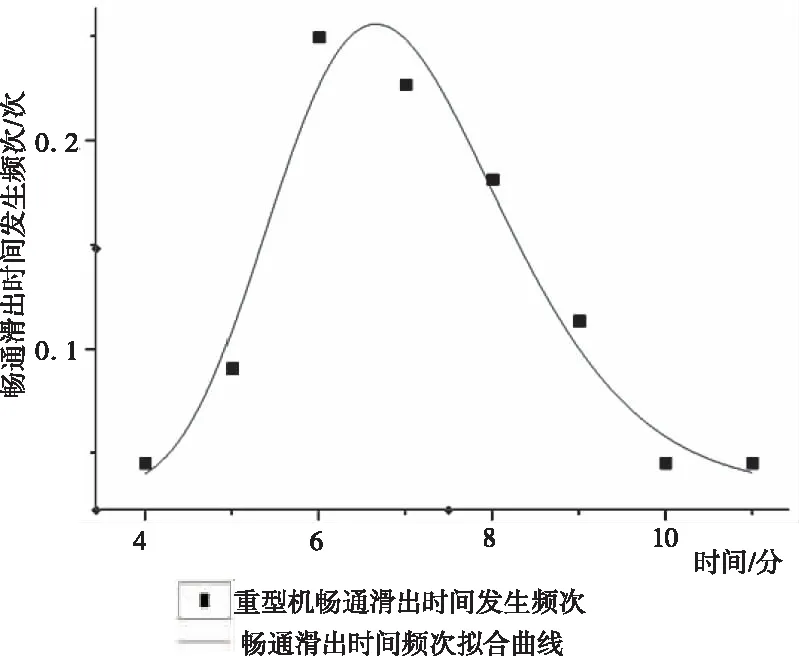
图2 重型机畅通滑出时间频率分布

El重=exp(μ+σ2/2)=7.05min

(5)

4)拥堵滑出时间

+1.60Dm+4.10As+2.25Ah+2.03Am

(6)

式(6)中：Ds和As分别是离场航空器l重从廊桥推出至起飞离地过程中，在36R跑道上A380的起飞和落地数量，架次；Dh和Ah分别是重型机的起飞和落地数量，架次；Dm和Am分别是中型机的起飞和落地数量，架次。

方程(6)的拟合优度R2=0.95。

3.2 中型机

1)整体拟合

首先对中型机l中的统计数据进行初步整体拟合，建立多元线性回归方程如下：

(7)

式(7)中：D和A分别为离场航空器l中从廊桥推出至起飞离地过程中，使用36R跑道起飞和落地的航空器数量。该模型的拟合优度R2=0.92。

2)分段拟合

同样使用最小二乘法，计算得出最优分段点为(1，1)，将样本数据的前半段区间用于计算畅通情况下的滑行时间，后半段区间用于计算拥堵情况下的滑行时间。

3)畅通滑出时间

在样本数据统计过程中，记y中为中型机畅通滑出时间的发生频率，建立对数正态分布模型如下：

y中=y0+c/(sqrt(2*PI)*σ*x)

*exp(-(lnx-μ)2/(2*σ2))

(8)

式(8)中：μ和σ分别为中型机畅通滑出时间对数的平均值和标准差，y0和c为常数。

使用正交距离回归算法对中型机样本数据进行回归分析，得到中型机畅通滑出时间频率分布的拟合函数如下：

y中=0.04011+0.64553/(sqrt(2*PI)*0.20094*x)

*exp(-(lnx-6.11947)2/(2*0.200942))

(9)

对应的拟合曲线如图3所示。

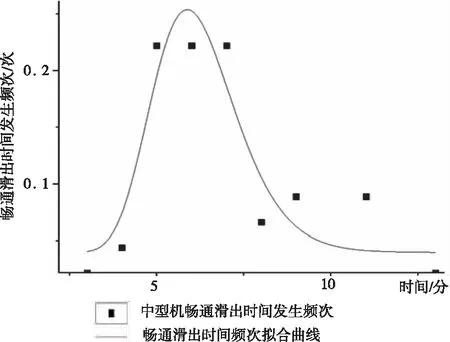
图3 中型机畅通滑出时间频率分布

根据式(9)中的μ和σ值，计算对数正态分布模型的期望值为：

El中=exp(μ+σ2/2)=6.24min

(10)

4)拥堵滑出时间

+1.62Dm+3.19As+2.06Ah+2.03Am

(11)

式(11)中，Ds和As分别是离场航空器l中从推出至起飞离地过程中，在36R跑道上A380的起飞和落地数量，架次；Dh和Ah分别是重型机的起飞和落地数量，架次；Dm和Am分别是中型机的起飞和落地数量，架次。

方程(11)的拟合优度R2=0.95。

4 模型的验证

为检验航空器地面滑出时间数学模型的预测准确度，选取停靠在1号停机位区域，且在不同时间段运行的航班数据进行验证。

4.1 重型机

1)畅通滑出时间验证

2019年7至10月，停靠在1号停机位区域，从36R跑道起飞重型机的实际畅通滑出时间和预测畅通滑出时间对比如图4所示。

图4 重型机畅通滑出时间的实际值与预测值

相同机位重型机畅通滑出时间的预测误差平均值为15.02%。

2)拥堵滑出时间验证

2019年7至10月，停靠在1号停机位区域，从36R跑道起飞重型机的实际拥堵滑出时间和预测拥堵滑出时间对比如图5所示。

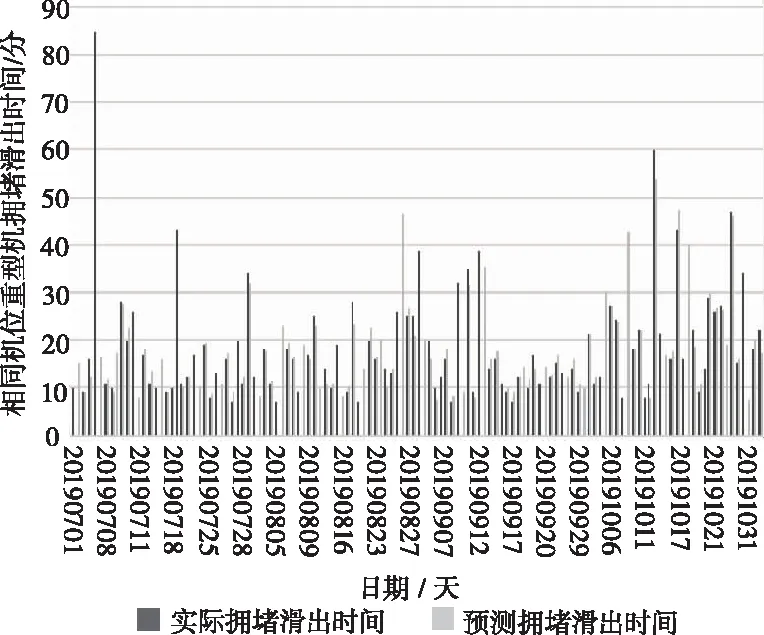
图5 重型机拥堵滑出时间的实际值与预测值

相同机位重型机拥堵滑出时间的预测误差平均值为11.55%。

4.2 中型机

1)畅通滑出时间验证

2019年7至10月，停靠在1号停机位区域，从36R跑道起飞中型机的实际畅通滑出时间和预测畅通滑出时间对比如图6所示。

图6 中型机畅通滑出时间的实际值与预测值

相同机位中型机畅通滑出时间的预测误差平均值为13.59%。

2)拥堵滑出时间验证

2019年7至10月，停靠在1号停机位区域，从36R跑道起飞中型机的实际拥堵滑出时间和预测拥堵滑出时间对比如图7所示。

图7 中型机拥堵滑出时间的实际值与预测值

相同机位中型机拥堵滑出时间的预测误差率均值为10.89%。

5 结论

针对目前航空器地面滑出时间数学模型在机型分类、样本数据区间选择、自变量选取、定义或计算方法等方面存在的不足，提出了新的航空器滑出时间计算方法，并用首都国际机场实际运行数据进行检验，验证结果表明：

1)数据区间分段方法可行。使用了最小二乘法寻找样本数据区间的最优分段点。该方法比之前使用的拟合斜率法更优，使重型机和中型机的畅通滑出时间预测误差率分别下降了1.71%和1.42%[13]；

2)数学模型的预测精度较高。经检验，1号机位区重型机和中型机畅通滑出时间的预测误差率分别为15.02%和13.59%，拥堵滑出时间的预测误差率分别为11.55%和10.89%；

3)考虑了不同机型的影响。①同等情况下，重型机比中型机的平均畅通滑出时间更长(在1号机位区域，前者比后者多0.81分钟)，因为重型机比中型机的推出开车时间更长；②从方程(6)和(11)可看出，落地航空器比起飞航空器对航空器拥堵滑出时间的影响更大，因为前者占用跑道时间更长；同时机型的尾流等级越高，影响越大，因为其占用跑道时间和开车时间均更长；

4)预测误差产生原因分析。①样本数据中缺乏部分航班的起降信息和穿越36R跑道的航班信息，数据的完整性受到影响；②航班运行时刻的统计单位没有精确到秒，数据统计的精确性受到影响；③虽剔除了约1%的异常数据，仍有部分数据受到天气、航路流量控制和更换跑道等因素的影响；

5)后续研究。在进一步完善样本数据收集基础上，建立更加精确的航空器地面滑出时间预测模型，为后续开展航空器在廊桥推出率的智能控制策略研究奠定基础。