椭圆切线的一种尺规作图新方法
2022-02-28重庆市铜梁二中邮编402560
重庆市铜梁二中 李 波 (邮编:402560)
以下是2021年5月高中数学联赛新疆赛区初赛的一道题目:在平面直角坐标系xoy中,曲线C1:(x+1)2+y2=16,曲 线过M(-1,0)斜率不为零的直线与C1交于A、B,N(1,0),线段AN、BN的 垂直平分 线分别 为l1、l2,求证:
(1)l1、l2均与C2相切;(2)l1、l2的交点P在定直线上.
不难看出,M、N恰好是椭圆C2的左、右焦点,圆C1的圆心是C2的左焦点且半径为C2的长轴长.那么,若将M、N的条件放宽成x轴上关于原点对称的点,结论是否成立呢?
1 推广
性质1如图1,设椭圆b> 0 ),圆C1:(x+m)2+y2=(2a)2(0 <m<a),过M(-m,0 )的斜率不为零的直线交C1交于A、B、N(m,0),线段AN、BN的垂直平分线分别为l1、l2,则
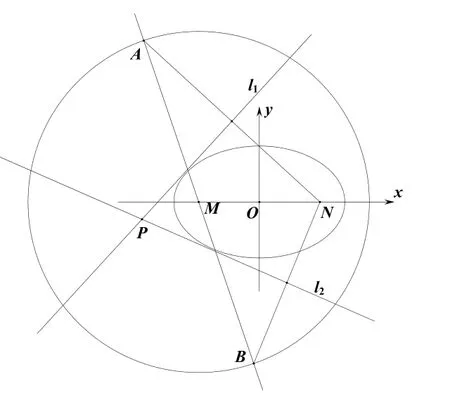
图1
(1)l1、l2均与C2相切当且仅当m=c,这里
(2)如果m=c,那么l1、l2的交点P在C2的左准线上.
证明(1)令∠AMx=θ(θ≠0),则A(2acosθm,2asinθ),AN的中点的坐标为(acosθ,asinθ).
当AN的斜率不存在时,l1的方程为y=那么,l1与C2相切当且仅当b=得m=c.此 时 ,A(c,±2b).由 于A、B关于M对称,得B(-3c,∓ 2b),则l2的方程为若l1的方程为y=b,则若l2的方程为y=-b,则结论成立.
当AN的斜率存在时由,则l1的方程为,与C2的方 程联 立 ,整 理 得[b2sin2θ+(m-acosθ)2]x2+2a(m-acosθ)(a-mcosθ)x+a2[(a-mcosθ)2-b2sin2θ]=0.于是,判别式
△=4a2b2sin2θ[b2sin2θ+(m-acosθ)2-(a-mcosθ)2]=4a2b2sin2θ(a2-b2-m2).
由于l1与C2相切等价于△=0,即a2-b2-m2=0,得m=c.
仿照上面的做法,可证l2与C2相切的情形.
(2)由于A,B关于M对称,则B(-2acosθm,-2asinθ).将 ① 中 的 sinθ,cosθ换 成-sinθ,-cosθ,得l2的方程因为m=c,由①-②整理得,
性质1的第一部分,也可以用几何方法证明.
如图2,F1、F2是椭圆1(a>b>0)的左右焦点,圆C1:(x+c)2+y2=(2a)2,过F1的斜率不为零的直线交C1交于A、B,线段AF2、BF2的垂直平分线分别为l1、l2.

图2
设直线AB与C2交于Q、H.连接QF2,则QF1+QF2=2a.因 为QF1+QA=2a,所 以QF2=QA,即Q在l1上.因此,Q是C2和l1的一个交点.在l1上任取异于Q的点Q′,连接Q′F1,Q′F2,则Q′F1+Q′F2=Q′F1+Q′A>AF1=2a,故Q′在椭圆C2之外.因此,l1与C2相切于点Q.类似地,l2与C2相切于点H.
双曲线也有类似的结论,即
性质2F1、F2是双曲线的左右焦点,过F1的斜率不为零的直线交圆C1:于A、B,线段AF2,BF2的垂直平分线分别为l1,l2,则
(1)l1、l2与C2相切;(2)l1、l2的交点在左准线上.
下面将利用性质1,得到如下结论.
性质3设椭圆的左、右焦点分为F1、F2,P是椭圆上异于左、右顶点的动点射线F1P与圆C1:(x+c)2+y2=(a+c)2交于点N,线段PF2与圆C2:(x-c)2+y2=(a-c)2交于点M,则线段MN的垂直平分线与椭圆E相切于点P.
证明因为|PF1|+|PF2|=2a,|MF2|=ac,所以|PF1|+|PM|=2a-(a-c)=a+c=|F1N|.于是|PN|=|PM|,即△NPM为等腰三角形.
如图3,作圆C3:(x+c)2+y2=(2a)2,并延长F1N交C3于点Q,连接QF2.由于QN=QF1-NF1=a-c=MF2,则进 而QF2//MN.因此,△NPM与△QPF2是一对相似的等腰三角形,则它们的底边的垂直平分线重合.另一方面,由性质1第一部分的几何证明过程可得:线段QF2的垂直平分线与椭圆E相切与点P.于是,结论成立.
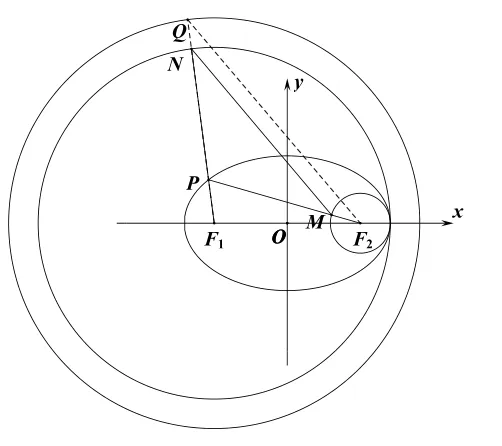
图3
事实上,性质3给出了用尺规作图求椭圆上一点(不是左右端点)切线的方法.设椭圆)的左、右焦点分为F1、F2,
第一步 分别以F1、F2为圆心作半径为ac,a+c的圆O1、O2;
第二步 在椭圆E上任取一点P,连结PF2交O2于M;作射线F1P交O1于N;
第三步 作线段MN的垂直平分线l;
由性质3,l是E在点P处的切线.
性质4设双曲线的左、右焦点分为F1、F2,P是双曲线E右支上异于右顶点的动点线段F1P与圆C1:(x+c)2+y2=(a+c)2交 于 点N,线 段PF2与 圆C2:(x-c)2+y2=(c-a)2交于点M,则线段MN的垂直平分线与双曲线E相切于点P.
2 相似椭圆的一个性质
在图1中,圆C1与x轴正半轴的交点与点N关于椭圆C2的右顶点对称,这样使得C1的半径始终是C2的长轴长.受此启发,发现了相似比为1:2的椭圆的一个性质.
性质5设M(-m,0),N(m,0),过M的斜率不为零的直线交C2于A、B,线段AN、BN分别与C1交于P、Q,则S△ABN=2S四边形MQNP.
证明如图4,设圆O:x2+y2=r2(r>0 ),圆M:(x+m)2+y2=(2r)2(-r<m<r,m≠0 ),M(-m,0),N(m,0),过M的斜率不为零的直线交圆M于A、B,线段AN、BN分别与圆O交于P、Q.连接OP,则AM=2OP.在△MNA和△ONP中,由余弦定理,得


图4
双曲线也有类似于性质5的结论.
性质6设双曲线
M(-m,0),N(m,0),过M的斜率不为零的直线交C2于A、B,线段AN,BN分别与C1交于P、Q,则S△ABN=2S四边形MQNP.
