2021年全国新高考数学Ⅰ卷第17题的解法探究和教学启示
2022-02-28广东省汕头市潮南区砺青中学郑灿基邮编515135
广东省汕头市潮南区砺青中学 郑灿基 (邮编:515135)
1 问题提出
(2021年新高考Ⅰ卷第17题)已知数列{an}满足
(1)记bn=a2n,写出b1、b2,并求数列{bn}的通项公式;
(2)求{an}的前20项和.
本题以“奇偶项交织”的递推关系考查数列的基本知识,注重基础,但形式新颖,解题方法较为丰富.
2 解法赏析
2.1 第(1)问解答
解法1由题设得b1=a2=a1+1=2,b2=a4=a3+1=a2+2+1=5.
因为bn+1=a2(n+1)=a2n+2=a2n+1+1=(a2n+2)+1=a2n+3.又bn=a2n,所 以bn+1=bn+3 即{bn}是以首项b1=2,公差为3的等差数列.
所以bn=2+3(n-1)=3n-1.
解法2由题设得b1=a2=a1+1=2,b2=a4=a3+1=a2+2+1=5.
b3=a6=a5+1=(a4+2)+1=5+3=8,于是猜测bn=2+3(n-1)=3n-1.
下面利用数学归纳法证明:
当n=1时,b1=2=3×1-1,显然成立;
假设当n=k时,bk=3k-1成立;
则当n=k+1时,
bk+1=a2k+2=a(2k+1)+1=a2k+1+1=(a2k+2)+1=a2k+3=bk+3=3(k+1)-1成立;
综上所述,bn=3n-1.
2.2 第(2)问解答
解法1
a1=1,a3=a1+3=4,a5=7,a7=10,a9=13,a11=16,a13=19,a15=22,a17=25,a19=28;
a2=2,a4=5,a6=8,a8=11,a10=14,a12=17,a14=20,a16=23,a18=26,a20=29.
设{an}的前n项和为Sn,
则S20=a1+a2+a3+···+a20=(1+4+7+···+28)+(2+5+···+29)
解 法 2由(1)得a2n=3n-1,又a2n=a(2n-1)+1=a2n-1+1,
所以a2n-1=a2n-1=3n-2.
(或a2n+1=a2n+2=3n+1)
又a1=1,所以a2n-1=3n-2.
设{an}的前n项和为Sn,
所以S20=a1+a2+a3+···+a20=(a1+a3+···+a19)+(a2+a4+···+a20)
=145+155=300.
3 解法探究
3.1 解法总结
按照题目的设计思路,结合以上解法,不难得出解题的思路是:首先是将奇偶项间的关系,转化为纯粹的偶数项的关系,进而发现偶子数列是等差数列,求出偶数项的通项公式a2n;其次是将a2n“返代”回递推式,求出a2n+1或a2n-1,进而可写出an的表达式.而实际上,我们也可以先研究奇子数列的关系.思路具体如下:
由 题 意 得a2n+1=a2n+2=a2n-1+1+2=a2n-1+3,即a2n+1-a2n-1=3.所以{ }a2n-1是以首项为1,公差为3的等差数列.所以a2n-1=1+3(n-1)=3n-2.所 以a2n=a2n-1+1=3n-1.

因此,关于“奇偶项交织”的递推关系求解通项这类问题的通性解法可以归纳:首先是将奇偶项间的关系,转化为纯粹的偶数项(或奇数项)的关系,求出偶数项(或奇数项)的通项公式a2n(或a2n-1);其次是将a2n(或a2n-1)“返代”回递推式,求出a2n-1(或a2n),进而可写出an的表达式.
3.2 试题内容的等价形式
本题中提供的数列递推模型中,当n为奇数时,an+1=an+1;当n为偶数时,an+1=an+2;由于数列 1,2,1,2,…,1,2,…可写成···,其通项公式为因此本题中数列递推模型可写成可以利用累加法求出其通项公式,即:
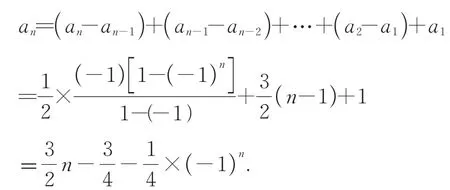
不难得到 ,a2n=3n-1,a2n-1=3n-2,所以{an}的奇子数列和偶子数列都为等差数列.
3.3 试题的拓展
由于递推公式的类型较多,下面主要以an+1=pan+f(n)(p为常数)进行分析举例.在an+1=pan+f(n)中,若f(n)中含有(-1)n这个结构,根据以上分析,可以将“奇偶项交织”的递推关系用分段形式进行表达呈现,例如:

类型an+1=■■■an+1,n为奇数,an+2,n为偶数.an+1=■■■an+n,n为奇数,an+n+1,n为偶数.an+1=■■■2an-2,n为奇数,2an+1,n为偶数.an+1=■■■2an+n-2,n为奇数,2an+n+1,n为偶数.类型等价形式an+1=an+3 2+1 2×()-1 n an+1=an+n+1 2+1 2×()-1 n an+1=2an-1 2+3 2()-1 n an+1=2an+n-1 2+3 2()-1 n求通项的方法3.1中总结的通性解法3.1中总结的通性解法3.1中总结的通性解法3.1中总结的通性解法累加法累加法构造数列为等比数列构造数列为等比数列
以上所举类型,通过等价改写,不仅解法上是多样的,而且对问题的本质、题目的思路设计都有很好的指导意义.但需要指出的是,以“奇偶项交织”的递推关系类型,有时等价写成“合二为一”的递推模型进行求解,并不利于解题,相反,可能会将问题复杂化.例如可以等价写成但是这样的改写,不能简化解题.相反,如果题目条件是以的形式呈现,我们反而要写成“奇偶项交织”的递推关系利用本文3.2中总结的通性解法进行求解.
3.4 举例说明
例1(2012年全国卷理第16题)数列{an}满足an+1+(-1)nan=2n-1,则 {an}的前 60 项和________.
解由题意得由a2n+1=-a2n+4n-1=-(a2n-1+2(2n-1)-1)+4n-1=-a2n-1+2.所以a2n+1-1=-(a2n-1-1),不 妨 设a1=t,若t=1,所 以a2n-1-1=0 即a2n-1=1,所 以a2n=a2n-1+4n-2-1=4n-2.所以S60=30×1+
若t≠1,{a2n-1-1}是以首项t-1,公比为-1的等比数列.所以a2n-1-1=(t-1)(-1)n,所以a2n-1=(t-1)(-1)n+1.所以a2n=a2n-1+2(2n-1)-1=(t-1)(-1)n+4n-2.
设{an}的前n项和为Sn,则S60=30×1+
点评由a2n-1=(t-1)(-1)n+1和a2n=(t-1)(-1)n+4n-2.可以看出求{an}的前n项和为Sn时,当n为偶数时,Sn的结果与a1的值无关,因此本题采用特殊法,取a1=1进行求解,过程会更简单些..
4 高考题对教学的启示
4.1 把脉高考命题方向
立足高中课程标准,研究高考真题,把脉高考命题方向是每位高中数学教师在进行高三复习迎考时的一项重要工作.从近几年的高考数列考查内容和方向来分析,变化不大,保持了较高的稳定性.建议在数列复习教学中,师生继续体悟数列的基本概念、基本性质、常用公式,能够熟练掌握研究数列通项公式与前n项和的基本方法,着重培养学生的逻辑推理、数学运算等数学核心素养.
4.2 提高数学运算能力
4.2.1 掌握求数列通项公式的常用方法
高考数列试题常以等差、等比数列的基础知识及综合运用为主.要会用“基本量思想”求解等差、等比数列的通项公式;能由具有特定特征的递推关系式求解通项公式(如累加法、累乘法等),并会通过“构造新数列”(如加常数、取倒数等)研究数列的通项公式;会利用an与Sn的关系求通项公式;会用归纳猜想的方法研究数列的通项公式,并能用数学归纳法证明之.同时,还应熟练掌握一些基本方法(如因式分解、配方法).
4.2.2 理解与掌握求数列前n项和的方法
要会熟练使用公式法、错位相减、裂项相消、分组求和、奇偶分析和并项求和等方法研究数列前n项和.这些方法中,有的方法是教材中公式推导所使用的方法,建议在数列复习教学中重视对公式的推导并借机发挥;有的方法是教材所配习题所需要使用的研究方法,师生也应积极交流并巩固认知.
4.2.3 加强运算能力的训练
数列解答题的计算量一般来说不大,但若涉及错位相减求和、奇偶分析和并项求和等方法,计算量会变大,非常容易出错.为了提高计算的速度和准确率,在平时教学中既要暴露计算问题,更要用充足的时间进行计算训练.
4.3 促成学生转化应用能力
纵观数列试题的命制,其考查内容离不开定义和性质,但考查的形式和角度不再单一化,而呈多样化的趋势.有时把数列知识巧妙渗透在数学文化中,考查学生分析问题和解决问题的能力,培养学生理论联系实际的能力;有时会给出新定义和新情景,要求考生在新定义和新情景中明晰数列知识的角色参与.这些题目的备考重点是学生要理解好数列的本质内涵,熟悉数列知识的背景,灵活利用已知解决未知,实现知识间的相互转化.
