航空发动机典型弯管的模态分析

2022-02-27王志国

中国民航大学学报 2022年6期

王志国

（中国民航大学工程技术训练中心，天津 300300）

管路振动已成为航空发动机系统安全运行的主要障碍之一。据统计[1]，90%的航空发动机故障与管路振动相关，且50%的航空发动机空停事件与其管路振动引起的结构失效有关，探究航空发动机核心机外部系统管路在发动机工作状态下的振动特性对于保障航空发动机正常运行具有重要意义。

国内外学者对航空发动机系统管路振动开展了相关研究。在理论研究方面：Mikota 等[2]针对液压管路振动构建了流体参数对管路振动特性影响的模型；孙欢[3]基于充液卡箍管路分析对称布局管路的振动模态及Von Misses 应力分布，并着重分析了管路长度对管内压力波动的影响；文献[4-5]针对复杂空间载流管路系统建立管路与基础、管路与管路的弹性连接结构模型，研究多个管路间的耦合振动规律；文献[6-7]引入黏弹性系数和脉动流因素建立加速度激励下的非线性流固耦合管路振动模型，研究重要流体参数对管路振动特性的影响；谭博欢等[8]以流体动力学方法获取的管内流体瞬时数据为激励建立管路的谐响应分析模型，重点研究管路振动瞬态特性。在试验研究方面：文献[9-11]通过锤击法振动试验研究基于实际尺寸模拟的管路粘结管接头及波纹管振动特性；文献[12-13]搭建空间管路系统试验台，使用锤击法开展输流管路的振动试验，研究管路在流固耦合作用下的振动模态变化规律；刘清友等[14]建立弯管试验台架开展振动试验，获取了单弯管关键部位的应变和振幅变化规律；于韶明等[15]针对航天器系统管路开展低量级的随机振动试验，分析高频振动环境对管路振动的影响特性；Hellstrom 和Fuchs[16]通过数值计算分析长流管振动特性；权凌霄等[17]将理论与试验结合分析充液管路振动激励特征和振动控制方法。当前研究多以普通管路为研究对象，针对弯曲结构管路的振动特性研究较少。Hambric 等[18]基于90°弯管研究了紊流对管路结构冲击的影响；文献[19-20]采用振动试验、数值模拟等方法研究充液弯管和塑性弯管的振动特性。

综上，以上研究主要关注航空发动机管路的数值计算与振动试验的高效性与适应性，较少涉及基于弯曲位置、弯曲程度等结构特征参数对管路振动特性的研究。为满足弯管结构设计标准要求[21]，降低发动机系统运行不安全事件发生率，本文提出以振动模态试验方法研究不同弯角、不同弯头长度（管路总长度保持不变情况下管路起点到弯曲处距离）的航空发动机系统弯管模型，通过研究弯管振动特性和管路振动变化规律，可为航空发动机系统管路的结构设计、适航维修提供技术支持。

1 管路振动特性理论分析

航空发动机管路系统的复杂性决定了管路振动特性的影响因素不是单一的，包括管路的固定形式、外观尺寸、结构特征等。为减少计算规模和难度，本文所研究管路不通入流体并简化管路的固定形式，选取两端固支，从管路结构特征角度分析弯管振动特性。

管路受外界振动激励时，管路振动特性包括管路固有频率变化和结构振型等表征。对于航空发动机管路系统，受发动机转子振动或外界振动激励时，系统运动方程可表示为

式中：M、C、K 分别为管路系统的质量矩阵、阻尼矩阵和刚度矩阵；分别为管路系统振型的位移、速度和加速度矢量；F（t）为管路系统受振动激励施加在管路系统上的外载荷，可表示为

式中：F0为初始激振力；i 为虚数单位；ω 为激振力频率；t为激励时间。

管路系统固有频率、阻尼比、响应静振型分别表示为

建模过程[6]采用分块兰索斯（Block Lanczos）法，该方法可用于视为壳体单元的管路计算方法分析。

2 弯管结构特征参数基本要求

发动机管路管径、弯曲半径存在限制和规范。依据文献[22]规定，要尽量减少航空发动机管路系统中管材、管径、导管弯曲半径、焊接方法等的规格和种类要求。与直管相比，弯管的结构特征参数主要体现在弯头长度l'和弯角α（或弯曲半径R）。而文献[22]附录B 规定钢和铝合金导管的最小弯曲半径应严格遵守文献[21]关于导管弯曲半径的要求。

（1）导管外径DN与导管弯曲半径R、最小弯曲半径Rmin之间关系的部分数据[21]如表1 所示。

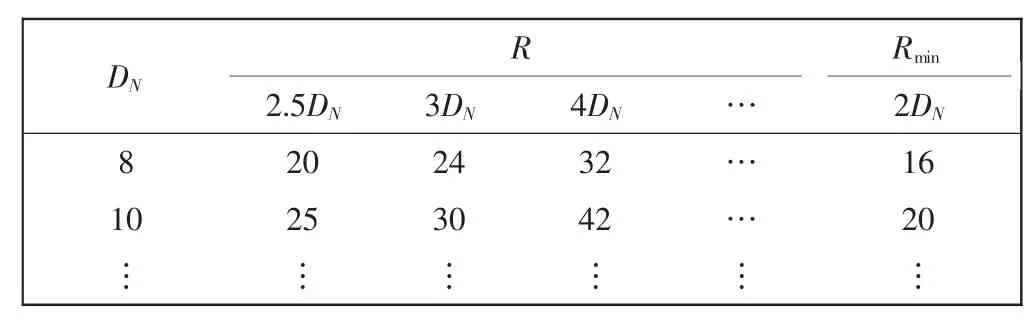
表1 导管弯曲半径Tab.1 Bending radius of catheter mm

（2）导管外径DN与弯头直线段l关系[21]为：当DN≤16 mm 时，l≥25 mm；当DN＞16 mm 时，l≥1.5DN。

（3）文献[23]关于螺纹管件弯头有明确要求：管路弯头弯角为45°、90°；同时根据工程需要，还存在135°，但各种弯头对流体流动的压降损失和受外界振动影响存在差异。

3 弯角变化的弯管振动特性

3.1 弯管模型构建

以弯头长度l'、弯角α 为弯管结构特征参数。基于管路易弯度、结构振动受阻尼影响小等实际要求，被测系统选取铝合金管材6061-T6（Al-Mg-Si 合金），该材料杨氏模量Ex=70 GPa、密度ρ=2 800 kg/m3、泊松比μ=0.33。选取直线段长度l=480mm，外径φ1=9.7mm，内径φ2=5.9 mm，厚度Δ=1.9 mm 为基本弯管模型，并以半径为25 mm 的弯管器形成半径R=26.67 mm 的不同结构弯管模型，如图1 所示。

图1 不同弯角的弯管模型Fig.1 Bending pipe models of the different bending angles

图1 中，保持弯头长度l'为210 mm 不变，建立弯角α 分别为0°、45°、90°、135°的4 个不同弯曲程度的弯管模型，设为弯管模型1～4。该弯管模型通过弯管器弯曲形成，在弯管模型1 基础上弯曲，拉伸长度Δl在0～6 mm 之内。

对照弯管结构特征参数基本要求，检验形成的弯管模型是否满足规范要求：

（1）弯管外径DN=9.7 mm、弯曲半径R=26.67 mm，满足表1 中DN∈（8，10）的导管弯曲半径、最小弯曲半径的要求；

（2）弯管外径DN=9.7 mm（≤16 mm），弯头长度l'最小值为80 mm（≥25 mm），满足导管外径与弯头直线段的关系要求；

（3）弯管弯角取为0°、45°、90°、135°也符合规范要求。

3.2 弯管振动特性趋势仿真分析

针对大长细比、薄厚度的层状壳体结构管路，选取Solid Brick 8 node185 单元类型，以Mechanical ADPL 15.0 分别构建弯管模型1～4 仿真模型，其中弯管模型4（弯头长度l'=210 mm、弯角α=135°）的仿真图如图2 所示。

图2 弯管模型4 仿真图Fig.2 Simulation diagram of bending pipe model 4

设置弯管模型1 网格尺寸分别为0.5、1.0、2.0 mm等，采用Manual Size 以面划分网格，得到的节点数分别为8 117、40 331、286 693；结构约束为带吸盘卡箍，约束线为管路两端各37 mm 长度上的8 条线，其中管路一端4 条对称约束线在管路圆形截面的18.02°、161.98°、198.02°、341.98°位置处，在两端固定约束加载，如图3 所示。

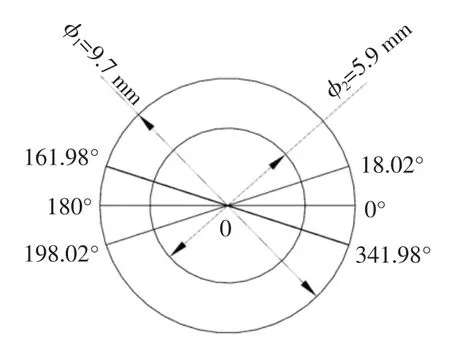
图3 管路约束线位置Fig.3 Location of constraint lines for pipes

采用Block Lanczos 法求解，计算3 种网格尺寸下管路前12 阶（结构模型受影响振动时产生的多个固有频率）固有频率，如图4 所示。

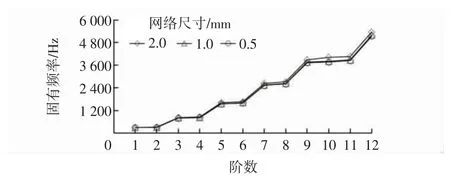
图4 不同网格划分的模型1 固有频率值Fig.4 Natural frequency value of model 1 with different mesh partitioning

由图4 可知，不同网格尺寸下，前8 阶中，3 种网格划分得到的结果比较一致；在后4 阶中，取2.0 mm 尺寸划分网格的计算结果与取0.5、1.0 mm 尺寸划分网络的计算结果差异较大，分别为4.41%、5.42%，3.06%、4.07%，3.04%、4.02%，5.13%、6.47%，远大于1%；而取1 mm 尺寸划分网格的计算结果与取0.5 mm 尺寸划分网格的计算结果差异较小，分别为1.01%、1.42%、1.06%、1.04%，接近1%；同时，取0.5 mm 尺寸划分网格得到的节点数比取1 mm 尺寸划分网络多了246 362 个节点，计算难度较大。为使计算结果准确，同时尽可能降低计算难度，取1.0 mm 为网格标准尺寸。

依据弯管模型1 的仿真建模方法，分别对弯管模型2～4 仿真建模，计算各模型振动模态参数值。由于管路振动同阶振型在x 和y 方向均对称显示，为计算简单，并与3.3 节弯管振动试验激励相应方向一致，取y 方向振动特性值计算，即显示奇数阶振动特性值（第1、3、5、7、9、11 阶），弯管模型1～4（弯角分别为0°、45°、90°、135°）固有频率如图5 所示。

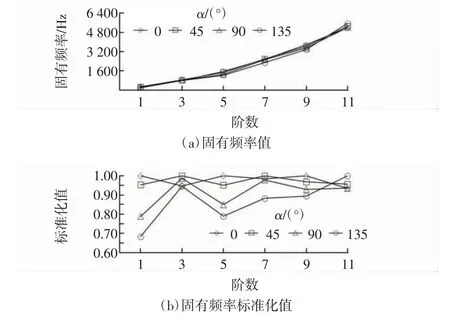
图5 不同弯角下弯管模型固有频率变化趋势Fig.5 Change trend of natural frequency of bending pipe model with different angles

从图5（a）可知，弯头长度（l'=210 mm）不变时，随着弯角α 增大，弯管模型1～4 固有频率存在变化，但差异较小；为精确分析各模型固有频率的变化关系，将各模型多阶固有频率值标准化处理，即弯管模型各阶固有频率值归一到（0，1）内，如图5（b）所示。从图5（b）可知，在弯头长度l'不变时，随着α 增加，弯管模型1～4 同阶固有频率值随弯角增大基本呈减小趋势，但减小趋势存在差异，减小幅度在（45°，90°）范围内显著增加，在（0°，45°）和（90°，135°）范围内减小幅度较小；但在第3 阶和第11 阶存在突变，减小幅度在（45°，90°）范围内增加不明显，甚至第11 阶固有频率不减反增至最大。这种振动特性主要由于管路弯曲拉伸过程中产生的结构损伤、阻尼等引起的，但不影响弯管模型1～4固有频率变化的总体趋势。

通过仿真计算可得到弯管模型1 中1～12 阶的结构振型，其中1、3、5 阶仿真结果与试验结构振型如图6 所示。由于试验结构振型仅存在1～3 阶，分别与仿真计算得到的1、3、5 阶相对应，因此，本文中只需对比分析仿真结果1、3、5 阶和试验结果1、2、3 阶结构振型即可。

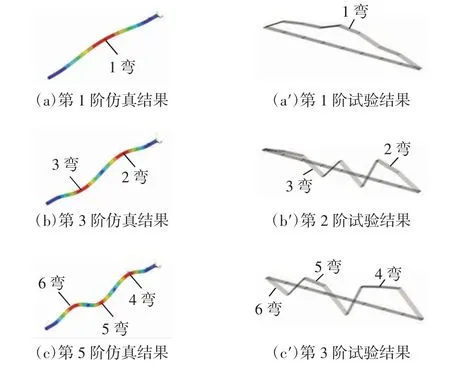
图6 弯管模型1 的结构振型图Fig.6 Structural deformation diagram of bending pipe model 1

从图6 可知，弯管模型1 的结构振型存在规律性，即结构振型从1～6 弯，弯曲方向含y+、x+、y-、x-等，在同一弯曲振型中，不同方向的弯曲振型共存形成扭转振型，即“从1～5 扭”，即从y+向x+扭转、从x+向y-扭转、从y-向x-扭转、从x-向y+扭转。

参考弯管模型1 的分析方法，分析弯管模型2～4，如图7～图9 所示。在弯头长度l'不变时，随着弯角与阶数增加，弯管结构振型从1 弯增加至6 弯，扭转从1扭增加至5 扭，弯曲段的弯、扭振型叠加呈现；同时，主结构弯曲与扭转振型、弯曲段弯扭振型程度逐步增加，对弯管非弯曲段的影响也呈累加增大趋势。从结构振动原理可知，不同弯角的结构特征影响使非对称的弯管结构以及非对称约束加载下的管路结构阵型在弯曲与扭转叠加中变化，呈现复杂性。

图7 弯管模型2 的结构振型图Fig.7 Structural deformation diagram of bending pipe model 2

图9 弯管模型4 的结构振型Fig.9 Structural deformation diagram of bending pipe model 4

3.3 弯管振动特性试验分析

搭建两端固支弯管模型管路试验系统，包括被测系统和测试系统如图10 所示。被测系统包括不同结构参数的弯管、用于固支管路的吸盘、TST3810 应变适调器；测试系统包括力锤、TST5912E 动态信号测试系统、TSTMP 模态分析系统、动态信号测试仪。

图10 振动测试与模态分析系统Fig.10 Vibration testing and modal analysis system

弯管模型1～4 的试验方案：在管路顶端沿轴向从左至右分别采集7、10、10、9 个测点，在弯曲段均匀设置3 个测点，弯管两端用吸盘式卡箍固支，将2 个应变片垂直粘贴在距弯管左端120 mm 处；各测点以力锤沿y-方向连续敲击给出激励；基于大长细比管路的结构特征，将弯管顶端测点数据赋给投影在xoy 平面上弯管水平两端的节点，以弯管水平投影平面替代真实弯管建模并示出结构振动振型，完成弯管模型1～4的振动试验。弯管模型1～4 试验得出的结构振型如图6～图9右侧图所示，固有频率值如表2 所示，并将其与仿真结果比较。

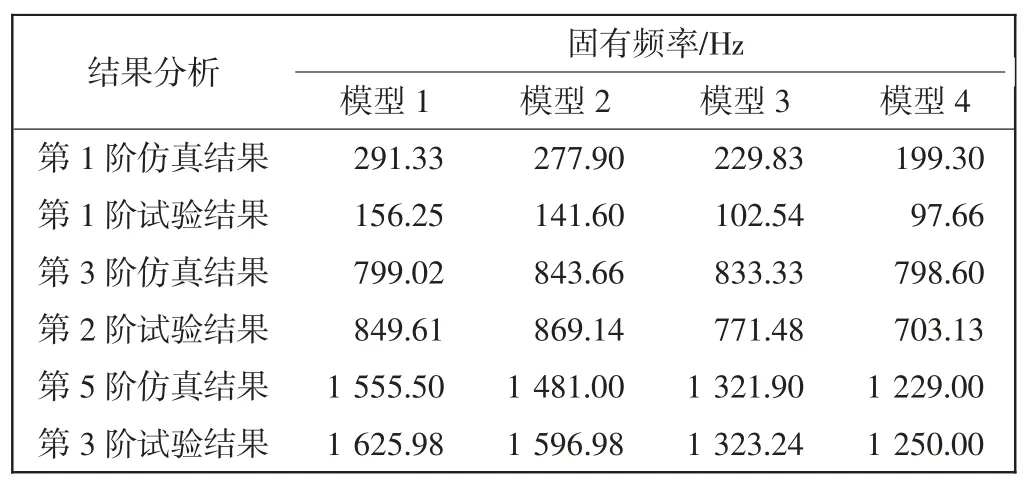
表2 弯角不同的弯管模型固有频率值Tab.2 Natural frequency value of the bending pipe models with different angles

从表2 分析可知，弯管模型1～4 第1 阶固有频率仿真结果与试验结果误差较大，在50%左右，主要是因为各模型的第1 阶固有频率绝对值较小，实际上各模型的误差绝对值只在100 Hz 左右；弯管模型1～4 的其他阶固有频率仿真与试验误差基本在10%内，只有弯管模型4 的第2 阶试验结果与第3 阶仿真结果误差超过10%，可能是卡箍不完全约束造成的。由此可得出，仿真得到的弯管模型固有频率值具有可靠性，可作为重要参数分析弯管模型振动特性。

其次，从图6（a'）—图6（c'）分析试验测得的弯管模型1 的振动结构振型，试验得到的1～3 阶主振型分别是1 个弯、2 个弯和3 个弯，与仿真得到的结构振型基本保持一致，存在的差异是试验得到的第2 阶振型由于卡箍的不完全约束，导致存在部分小振型；从图7（a'）—图7（c'）分析弯管模型2 的振动结构振型，试验得到的1～3 阶主振型分别是2 个弯+弯曲段1 个弯、2 个弯+1 个扭+弯曲段1 个弯、2 个弯+弯曲段2 个弯，与仿真得到的结构振型基本保持一致，存在的差异是试验得到的1～3 阶振型存在部分小振型，这也是由于卡箍的不完全约束及试验精度引起的；从图8（a'）—图8（c'）分析弯管模型3 的振动结构振型，试验得到的1～3 阶主要振型主要显示在y方向上，而x、z方向由于试验模态分析系统只能同时示出一个方向的局限而在振型上无法示出，故试验得到的1～3 阶主振型主要在与弯曲段接触的近端，为1 个弯、2 个弯、3个弯，没有示出扭转振型，振型在弯曲段显现，与得到的y方向的仿真结果保持一致；从图9（a'）—图9（c'）分析弯管模型4 的振动结构振型，试验得到1～3 阶主振型分别是2 个弯、2 个弯+1 个扭、2 个弯+2 个扭，与仿真得到的结构振型保持一致，存在的差异也是试验得到的1～3 阶主振型存在部分小振型，由卡箍不完全约束及试验精度引起的。因此，从模型的结构主振型看，仿真计算得到的弯管模型结构振型具有可靠性，可分析弯管模型振动特性。

图8 弯管模型3 的结构振型Fig.8 Structural deformation diagram of bending pipe model 3

由此确定试验得到的各模型结构振型比较复杂：如第1 阶主振型出现在第1 弯与第2 弯之间，并随着弯角增加出现结构扭转，同时，试验得到的结构振型伴随着大量的小振型；第2 阶主振型为2 个弯，随着弯角增加，逐步出现1 个扭转，弯曲段还出现1 个弯，结构振型也伴随着大量的小振型；第3 阶主振型在第2 个弯与第3 个弯之间，随着弯角增加，逐步出现2个扭转，弯曲段出现1 个弯、2 个弯振型。故从主振型角度分析，弯头长度l'不变时，随着弯角α 增加，当阶数从1 阶增加到3 阶时，弯管模型结构主振型从1 弯、2 弯变化到3 弯，扭转从1 扭变化到2 扭，弯曲段结构振型也从1 弯变化到2 弯，结构振型总体呈现出弯曲、扭转、弯曲段弯曲程度不断增大的累加趋势，与弯管模型1～4 仿真计算结果呈现的变化趋势基本一致。

弯管模型1～4 固有频率及标准化处理结果如图11 所示。从图11（a）可知，随着α 增加，弯管模型1～4的第1、2 阶固有频率变化较小，只是在第3 阶存在明显差异，但难以显示差异；从图11（b）分析各模型的固有频率标准化值的变化趋势，各模型的1～3 阶固有频率多随着α 增加而减小，只在第2 阶弯管模型1、2 间固有频率值增加，可能是因为从弯管模型1 的直管转变为弯管模型2 的弯管，拉伸因素使弯管结构刚度、阻尼等不规则变化引起的，同时，当α 在（45°，90°）范围内，与（0°，45°），（90°，135°）相比，各模型的同阶固有频率标准化值变化差异较大。

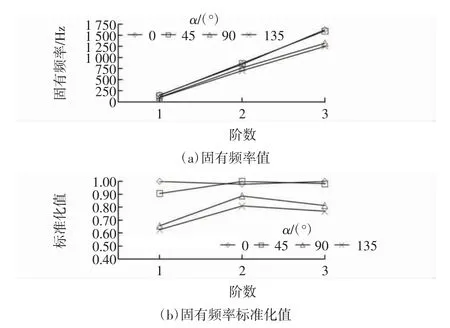
图11 不同弯角弯管模型振动试验固有频率变化趋势（α 变化）Fig.11 Change trend of natural frequency of bending pipe model vibration test with different angles(α change)

基于固有频率振动试验，在弯头长度l'不变时，随着弯角α 增加和阶数从1 阶增加到3 阶，弯管模型同阶固有频率总体上减小，但减小幅度在（45°，90°）范围内显著增加，在（0°，45°）和（90°，135°）范围内则减小幅度较小。这与弯管模型1～4 仿真计算结果呈现的变化趋势基本一致，故可确定数值仿真计算出的弯管振动特性是可靠的。

4 弯头长度变化的弯管振动特性

参照弯角α 变化得到弯管振动特性的方法，计算基于弯头长度l'变化的弯管振动特性。

按照图1 设置“弯头长度l'=210 mm 不变、弯角α变化”的弯管模型的方法，设置“弯角α=45°不变、弯头长度l'变化”的弯管模型5～9，如图12 所示。各模型弯头长度l'为80、160、240、320、400 m，分别采用5 个480 mm 长的直管拉伸弯曲45°制成，拉伸长度Δl 均为3 mm。

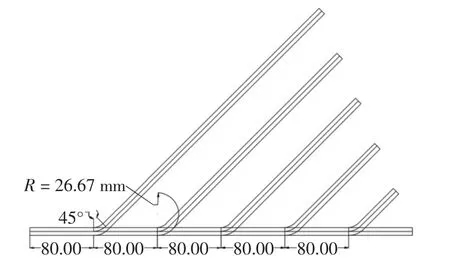
图12 不同弯头长度的弯管模型Fig.12 Bending pipe model with different head lengths

以ANSYS 仿真软件计算弯管模型5～9，得到全约束固支状态下不同弯头长度模型的振动固有频率值和结构振型，如图13 和14 所示。图13（a）为弯管模型5～9 的各阶固有频率值（基于弯管结构振型x、y 方向的重叠性显示，在此示出相关的第1、3、5、7、9、11阶）；图13（b）为将弯管模型5～9 固有频率值同阶标准化处理后的相对值；图14 为模型5～9 第1 阶和第11 阶结构振型图，图14（a）—图14（e）中左侧为第1 阶结构振型图，右侧为第2 阶结构振型图。

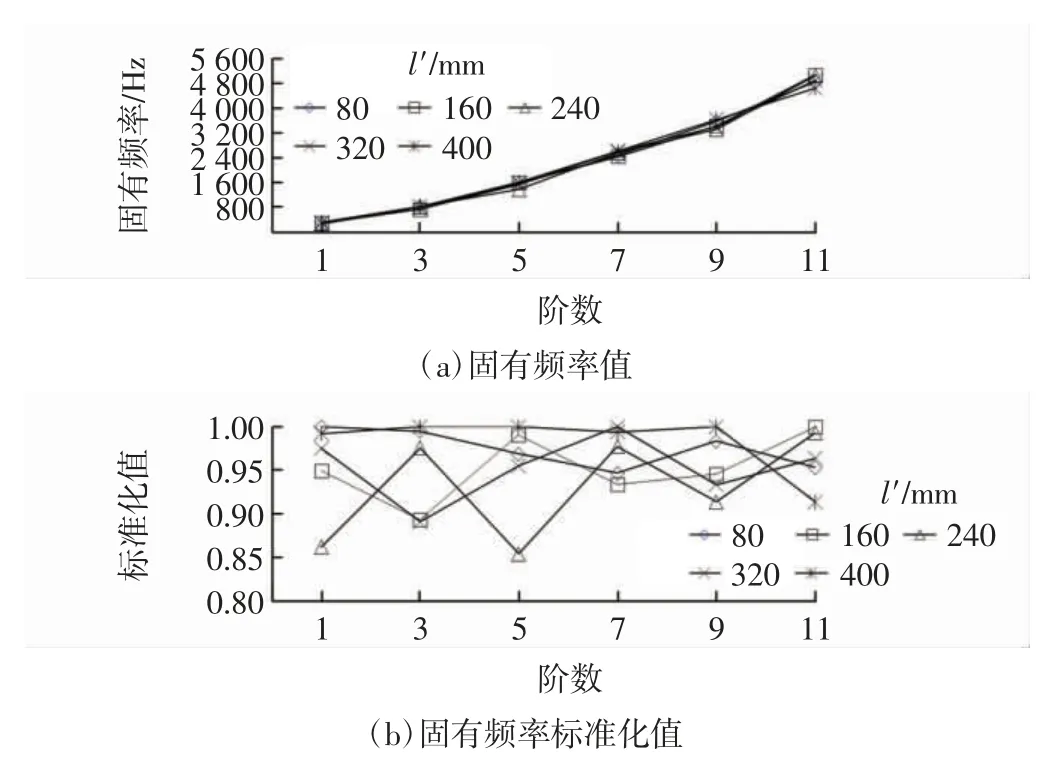
图13 弯管模型固有频率变化趋势（l′变化）Fig.13 Change trend of natural frequency of bending pipe model（l′change）

图14 不同弯头长度弯管的结构振型（第1 阶和第11 阶）Fig.14 Structural deformation of the bending pipes with different head lengths(1st and 11th steps)

从图13（a）可知：随着弯头长度l'和阶数增加，弯管模型5～9 的各阶固有频率存在差异但区分度同样较小；从图13（b）可知：随着l'和阶数增加，各模型同阶固有频率标准化值基本呈先减小后增加趋势，在l'=240 mm 时固有频率最低，这一趋势在第1、5、9 阶特别显著；但在第3、7、11 阶，随着l'增加，弯头长度l'左右两端对应的弯管模型，标准化值固有频率值接近，且在l'=240 mm 处固有频率居于其他模型之间，总体呈现对称模型固有频率标准化值一致、固有频率减小增加交替变化复杂变化态势。

从图14 可知，弯管模型5～9 结构振型是弯曲（多个）与扭转（多个）叠加。随着l'和阶数增加（以第1、11阶为例），振型从1～6 弯、1～5 扭，弯曲段振型弯曲与扭转振型叠加、个数逐渐增加、幅度逐步增大；同时，由于240 mm 处为管路中心，l'≤240 mm 模型与l'≥240 mm模型结构振型对称，呈现向远端移动与近远端振型交错。

5 航空发动机管路弯管段实例分析

选取两种金属材料的燃油管路，如普通不锈钢1Cr18Ni9Ti（20 ℃时，该材料的密度ρ= 7 900 kg/m3、杨氏模量Ex=184 GPa、泊松比μ=0.3）和航空航天专用管材TA18（20 ℃时，该材料的密度ρ=4 470 kg/m3、杨氏模量Ex=96 GPa、泊松比μ=0.39）。依此建立弯管模型10～15。

弯管模型10 采用1Cr18Ni9Ti，模型11 采用TA18材料。2 个模型管路尺寸一致，外径φ1=9.7 mm，内径φ2=5.9 mm，厚度Δ=1.9 mm，弯头长度l'=60 mm，弯管处弯曲半径R=30 mm，弯角α=45°，弯曲后管长为50 mm，通过弯管器弯曲后管路伸长量Δl=0.6 mm。

模型12 采用1Cr18Ni9Ti，模型13 采用TA18材料。2 个模型管路尺寸一致，且除弯头长度l'=80 mm外，其他尺寸与模型10、11 一致。

模型14 采用普通不锈钢材料，模型15 采用TA18材料。2 个模型管路尺寸一致，且除弯角α=45°、通过弯管器弯曲后管路伸长量Δl=1 mm 外，其他尺寸与模型10 和模型11 一致。

对弯管模型10～15 仿真建模，按照图4 的全约束加载方法加载计算，得到各模型的模态参数值。图15为弯头长度不同的两种材料弯管模型的固有频率各阶变化图，图16 为弯曲角度不同的两种材料弯管模型的固有频率各阶变化图。

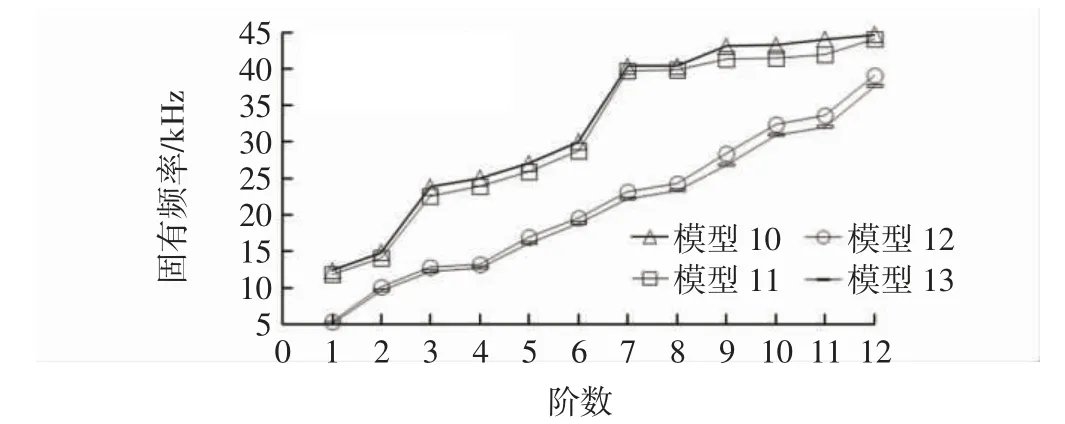
图15 弯头长度不同的弯管模型固有频率变化Fig.15 Variation of natural frequency of bending pipe model with different bending heads

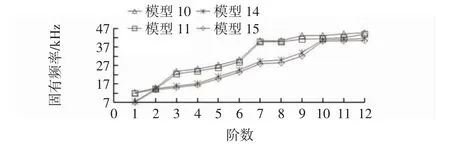
图16 弯角不同的弯管模型固有频率变化Fig.16 Variation of natural frequency of bending pipe model with different angles

从图15 可知，相同尺寸的弯管模型，TA18 和1Cr18Ni9Ti 材料相比，前者的各阶固有频率值都比后者小。当其他尺寸一致时，随着弯头长度增加20 mm时，各阶固有频率值显著下降，且两种材料的弯管模型均呈现该变化趋势，与图13（b）所示管路振动特性符合。

从图16 可知，相同尺寸的弯管模型，TA18 和1Cr18Ni9Ti 材料相比，前者的各阶固有频率值都比后者小。当其他尺寸一致时，随着弯曲角度在（45°，90°）增加时，各阶固有频率值显著下降，但在第2、10、11阶差距较小，但也保持下降趋势，且两种材料的弯管模型均呈现该变化趋势，与图5（b）所示的弯管振动特性符合。

同时，弯管模型9 和模型10 的各阶结构振型与图11—图14 在振型类型、振型峰值位置等存在复杂的关系，这与图6—图9 所示管路振动特性变化趋势相似，基于篇幅限制不再赘述。

从以上不同材料弯管的固有频率与振型的分析比较可知，使用TA18 航天专用管材的管路具有固有频率普遍小的特征，且在受到振动影响时结构振动特性变化复杂。