基于PSO-Elman神经网络的激光雷达径向风速预测

林家泉，宋德龙，庄子波，李金凤

（中国民航大学a.电子信息与自动化学院；b.飞行技术学院；c.经济与管理学院，天津 300300）

飞机起降过程受风的影响较大，尤其是周边地形复杂的机场，受太阳辐射、地形及复杂天气系统等因素的影响，近地面的风场会呈现出强烈的非线性。大气湍流强度大，其非线性、非平稳性、时变性突出，这将导致飞机无法正常降落，严重时会导致飞行事故，较大地影响飞行安全和飞行效率。因此，提供更加精细的风场信息及为湍流预警提供支撑一直是研究的热点和难点。

目前，相干激光雷达已经广泛用于民航机场湍流探测和预警中，是晴空条件下探测风场的有效手段[1-3]。张战盈等[4]通过3 台激光雷达组成的探测系统进行风场反演，其探测结果与传感器相比，具有良好的一致性。在测风方面，激光雷达在探测过程中可能会漏报小尺度湍流，且激光通过湍流区域时，将引起光强闪烁，导致接收端光信号随机衰落，严重时会引起激光信号消失，对风速的测量造成影响[5]。

神经网络在建立非线性数据间的函数映射、预测方面应用广泛[6-7]。在风速预测方面：Kumar 等[8]运用前向神经网络进行天气预报，但其网络结构比较简单，预测精度较低；叶瑞丽等[9]基于改进的Elman 神经网络对短期风速序列进行了预测，其结果与实测数据具有较好的一致性；Mishra 等[10]应用逆神经网络对风速序列进行预测，在输入层使用LP（legendre polynomial）函数对训练数据进行处理，并应用多种内核函数提升网络预测性能，但在极端天气条件下，尤其是在风速骤变或湍流发生时，实际风场呈非线性变化。上述条件下，神经网络在训练过程中产生过拟合或发散等情况，导致泛化能力降低，网络预测出的风速与实际风速相差较大。

综上所述，为提供更丰富的风场信息，降低湍流预警的漏报率，在雷达探测现有数据的基础上，对风速进行预测，实现精细化风场的目的，降低网络自身的不足与极端天气对风速预测带来的负面影响。本文结合激光雷达的多组回波信号数据，将粒子群（PSO，particle swarm optimization）算法与Elman 神经网络结合，对湍流风场的非线性和高时变性的风速进行预测。将雷达测出的谱宽、信噪比、回波距离作为粒子群优化Elman 网络的输入，通过PSO 算法优化Elman 神经网络，避免在训练初始时对内部权值、阈值进行随机赋值，提高了风速预测模型的预测精度。

1 风速预测模型的相关理论

1.1 Elman 神经网络

Elman 神经网络是一种动态的、反向传播机制的神经网络，其优势在于网络内部有一层特殊的反馈神经元（状态层），可将隐含层的输出进行延时与储存，反馈至隐含层的输入，从而解决动态建模的问题。风速的变化与其上一时刻的风速有较大的相关性，通过构建状态层提高神经网络处理风速动态信息的能力。因此，为准确预测出径向风速，选择Elman 神经网络建立风速预测模型，其中：隐含层的传递函数为tansig（）；输出层的激活函数为purelin（）；训练函数为traingdm（）。

在训练中Elman 神经网络存在过拟合、梯度发散等问题，因此，在Elman 神经网络上使用正则化策略并增加惩罚因子，适当地减小权值幅度，进一步提升预测风速的泛化能力。

1.2 粒子群优化Elman 神经网络

Elman 神经网络是由数据驱动、以梯度下降的原则进行传播的。虽然单一网络对于变化较小的风场有良好的预测效果，但在训练开始前网络内部的权值、阈值是随机赋值的，可能会导致网络无法对变化剧烈的数据进行有效预测。在数据量一定的情况下，需要风速数据对内部的权值、阈值进行调节，但当风速变化剧烈尤其是湍流发生时，单一网络不能充分地学习风速信息，其预测效果受到了一定的影响。

为提高Elman 神经网络在湍流发生时的预测精度，需要得到适应于实际风场Elman 神经网络的参数。因此，将Elman 神经网络与粒子群结合，运用粒子群对网络训练初始时的权值、阈值进行优化，将其最优解应用于Elman 神经网络中，再对Elman 神经网络进行训练，提升该网络针对风速变化大、湍流发生时预测的有效性。

粒子群算法是一种模拟鸟类集群觅食的寻优算法[11]，算法的步骤如下。

步骤1在预设维度的解空间内，以适应度函数fg（t）作为评价指标进行寻优求解，fg（t）为Elman 神经网络中最小均方差代价函数[12]，表示为

式中：M为训练数据总数；vi为测量风速；yi为网络预测输出；t为迭代步数。

步骤2在每次迭代中求出每个粒子的位置、速度和个体最优解pb，i（t），并将所有的个体最优解进行比较，选出误差最小的pb，i（t）作为此次迭代下的全局最优解gb（t），其计算[13]如下

步骤3根据gb（t）和pb，i（t），对下次迭代中粒子i的速度Vi（t+1）、位置Li（t+1）进行更新[13]，即

式中：ω为惯性系数；c1、c2为加速因子；r1、r2为[0，1]的随机数。

步骤4根据预设的迭代步数与结果误差终止计算，得出寻优结果。

将粒子群搜寻出的全局最优位置作为Elman 神经网络的权值和阈值。粒子群优化Elman（PSO-Elman）神经网络的算法流程如图1 所示。

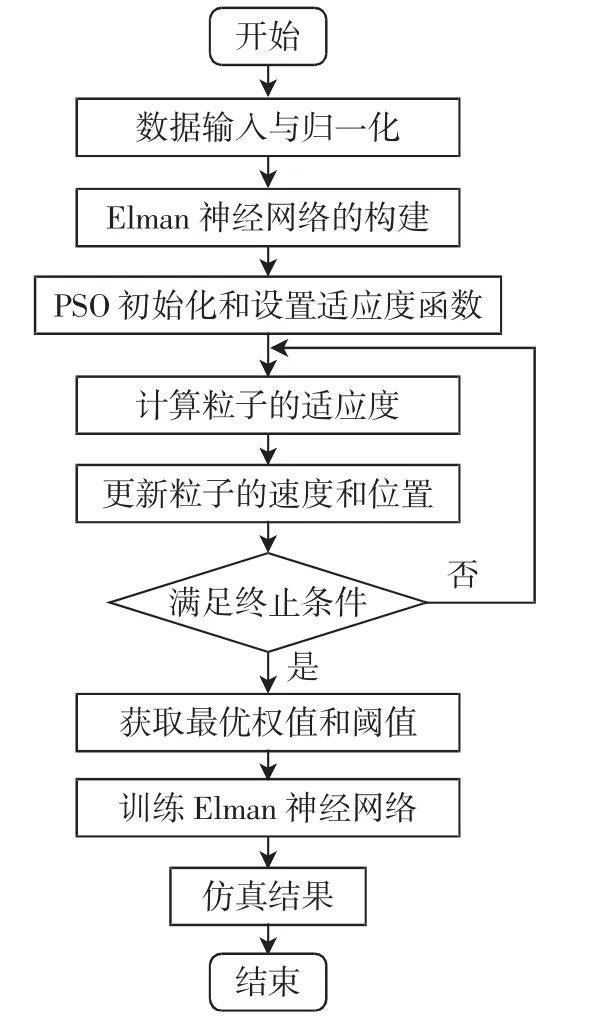
图1 PSO-Elman 神经网络预测风速的算法流程Fig.1 Flow chart of predicting wind speed by PSO-Elman neural network

为验证模型预测性能，将PSO-Elman 与Elman 神经网络进行比较，结果如图2 所示。

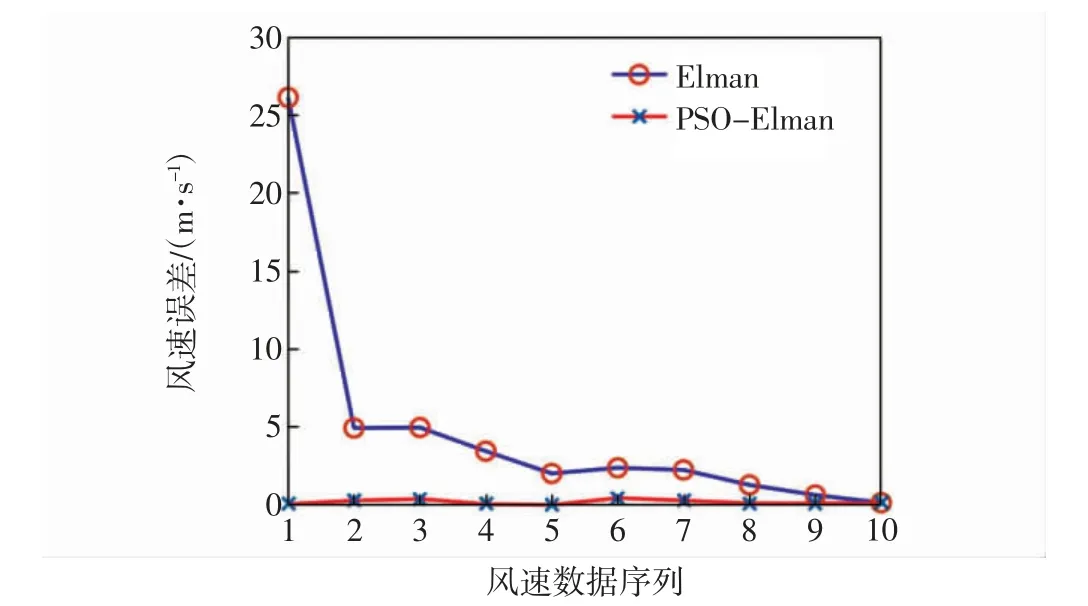
图2 两种风速预测模型的误差分析Fig.2 Error analysis of two wind speed prediction models

从图2 可以看出：相比于单一的Elman 神经网络，PSO-Elman 神经网络使得模型更加贴近实际情况，在收敛速度与预测精度上得到了提高。

2 预测模型建立

2.1 输入数据的相关分析

径向风速由激光雷达所接收回波信号的多普勒频移反演得出。回波信号的谱宽、信噪比和回波距离都会影响反演风速的精度。因此，认为这3 类数据的组合与所测的风速有复杂的非线性映射关系，所以将多维输入数据用于PSO-Elman 神经网络进行训练后，对径向风速进行预测。

谱宽表征取样体积内散射粒子多普勒速度与平均值的偏差程度。雷暴、风切变、湍流等极端天气条件下的风速与时间呈非线性关系，且信号呈高谱宽现象[14]。空域内有大气湍流等多变天气时，往往会导致回波信号谱宽的不规则变化。另一方面，根据文献[14]，采用激光雷达探测风速，经过计算得出湍流的耗散率，而文献[15]采用谱宽得出湍流耗散率，认为谱宽与径向风速存在一定的函数关系。因此，采用谱宽作为神经网络的输入。

信噪比是激光雷达系统中数据处理的重要参数，且影响回波信号的多普勒频移精度，其表示[16]为

式中：Ps表示雷达在一定时间内接收回波信号的光电子数；PN表示在同样时间内雷达收集的所有噪声光电子数。激光雷达将回波光子进行累积反演出径向风速，因此，信噪比影响雷达系统对径向风速的反演。另一方面，由文献[17]提出的激光雷达信噪比与最大似然离散谱峰值估计（ML-DSP）概率密度的关系，信噪比越大，信号估计的标准差越小。在实际测量中，信噪比的大小表示测量点所测信息的可信度，信噪比越大，风速误差越小。因此，采集信噪比作为神经网络的输入。

相对于雷达不同的距离，接收的回波信号也并不相同。因此，不同的距离和风速的变化有着一定的相关性，认为距离的变化对模型风速的预测有一定的辅助作用。另一方面，激光回波功率大小由激光朗伯体反射传输模型[18]得到，即

式中：Pr是激光回波功率；Pt是激光发射功率；St是目标反射率；Tr是接收系统效率；Tt是发射系统效率；Ar是接收光学面积；θ 是入射光线与法线的夹角；R是回波距离；Ua是大气衰减系数。激光雷达在工作中功率恒定，由式（6）可知，Pr与R2呈反比。R增大，Pr降低，会减少雷达望远镜接收回波信号的光子数量，进而对风速测量产生一定影响[19]。近似认为回波距离与当前风速有一定的拟合关系，采用回波距离作为神经网络的一个输入量。

综上所述，将激光雷达的这3 类数据作为PSOElman 神经网络输入数据进行风速预测，其部分神经网络输入和输出数据示例如表1 所示。

表1 部分神经网络输入和输出数据的示例Tab.1 Illustration of partial input and output data of neural network

2.2 数据归一化

激光雷达在探测过程中，受雷达本身累计误差等因素影响，造成某点与其临近测量点数值量纲上差异过大，会降低网络的预测精度。因此，应用归一化方法将输入数据转化为[0，1]范围内，使所有的测量点统一在同一数值量纲级别，降低网络波动，并保留数据信息的完整性，归一化的公式如下

式中：x为待归一化的输入数据；xmax、xmin为输入数据中的最大值和最小值；y为归一化后的数据。

2.3 PSO-Elman 神经网络参数设置与结构建立

为提高Elman 神经网络的预测性能，降低预测风速与测量风速之间的误差，隐含层节点数计算如下

式中：I为输入节点数；O为输出节点数；α 为0～9 的整数。由式（8）得出隐含层节点数的范围为[2，11][20]，通过分别构建不同S值的网络仿真实验，得出不同隐含层数目的网络平均误差，如表2 所示。

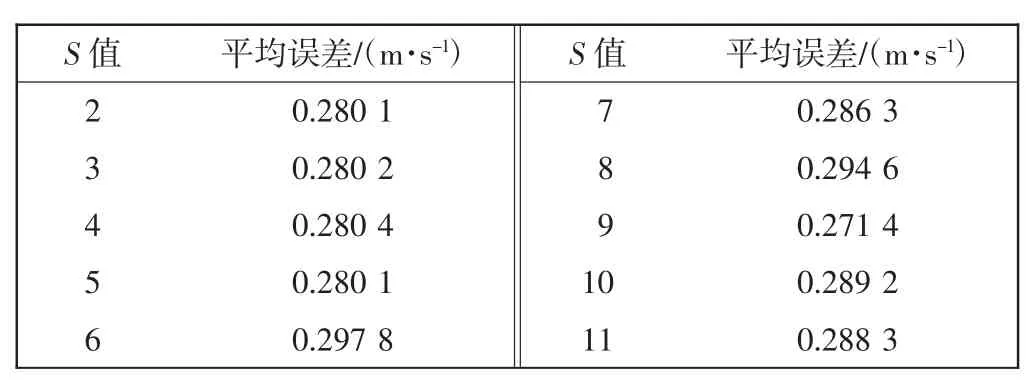
表2 不同S 值所对应的Elman 神经网络平均误差Tab.2 Network average error corresponding to different S values

由表2 可知，S=9 时，神经网络的平均误差最小，因此，本文选取的隐含层个数为9。又因Elman 神经网络隐含层的节点都相应地与状态层的节点连接，所以状态层的节点数目与隐含层的节点数目一致。由构建好的Elman 神经网络结构可以得出粒子群解空间维度为127，在确立粒子群解空间的维度后，将粒子群优化得出的最优解依次分配给Elman 神经网络结构，网络结构如图3 所示。其中，W1={W1，1，W1，2，…，W1，81}是状态层的权值（节点数与隐含层一致）；W2= {W2，1，W2，2，…，W2，27}是输入层权值（节点数为3）；W3={W3，1，W3，2，…，W3，9}是输出层权值（节点数为9），且该网络阈值数与每层的节点数相同。

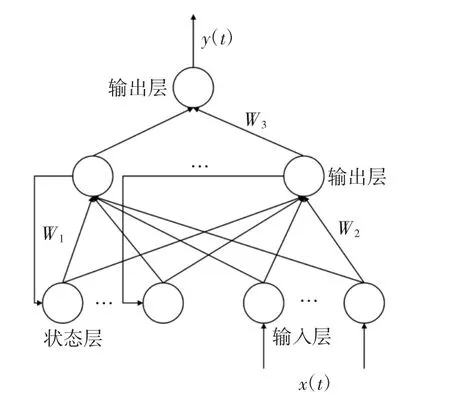
图3 Elman 神经网络结构Fig.3 Structure of Elman neural network

3 实验验证

本文采用位于兰州中川国际机场的1.55 μm 相干激光测风雷达进行实验测量。激光雷达实验装置如图4 所示，激光雷达的相关参数如表3 所示。

图4 激光雷达实验台Fig.4 Lidar experiment platform

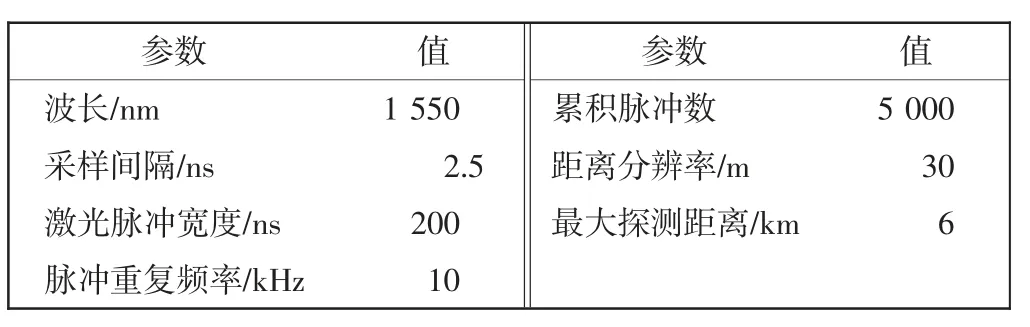
表3 激光雷达的相关参数Tab.3 Related parameters of lidar

激光雷达采用平面显示（PPI，plan position indicator）的扫描方式，在仰角不变的条件下进行全方位扫描，获取二维平面下的风速信息。图5 所示为PPI 扫描示意图，激光雷达位于圆心位置。

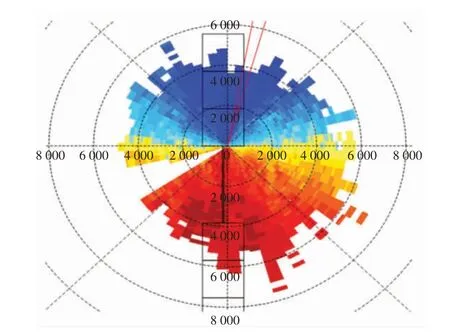
图5 PPI 扫描方式Fig.5 Illustration of PPI scan

选取上述激光雷达实验平台在2018年5月某天的遥感数据作为风速预测模型的输入数据，并在PSOElman 神经网络上进行训练。为验证PSO-Elman 神经网络的收敛性，将数据集的540 组数据分为490 组训练数据和50 组测试数据。将数据集中50 组测试数据输入至训练后的网络中，如图6 所示。

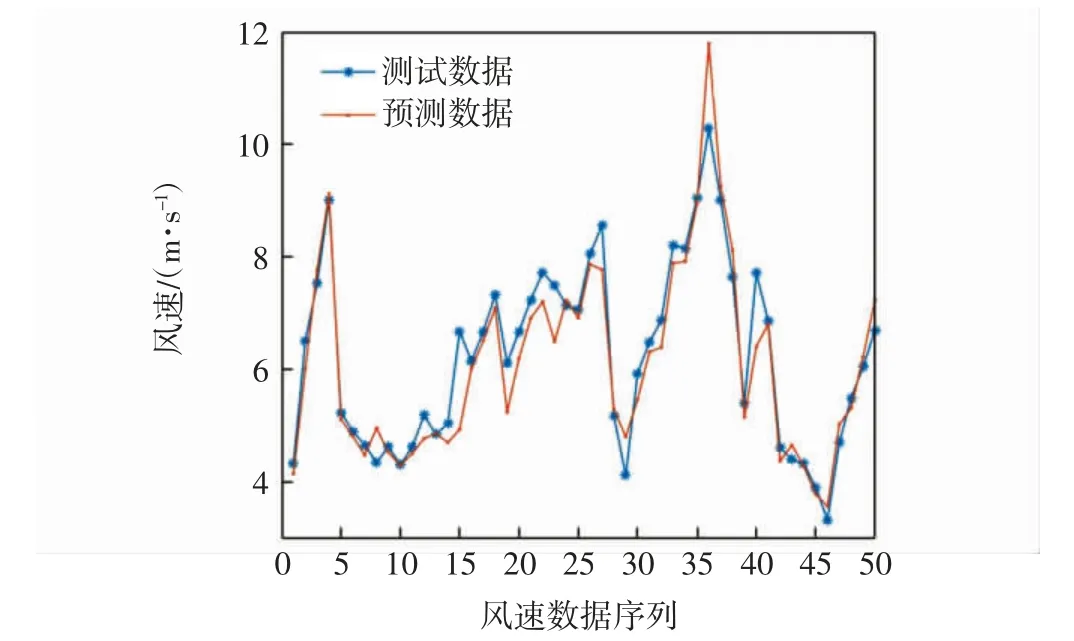
图6 测试与预测风速对比Fig.6 Comparison of test and predicted wind speed

从图6 中可看到PSO-Elman 神经网络预测的风速与测试数据的风速趋势基本一致，二者误差较小，且相对误差为4.37%，表明经过训练后模型与实际风场模型相关度较高，拟合程度较好。比对过程证明了经过训练后PSO-Elman 神经网络能够有效地对实际风速进行预测。

在激光雷达风速反演的基础上，在每个距离门中点添加由网络预测出的风速，实现精细化风场的目的。风速精细化反演示意如图7 所示。

图7（a）为原始雷达所测风速场，每个纵向距离门的间距为30 m，将距离门预测出的风速置于原始风场中，此时每个纵向距离门的间距缩至15 m，如图7（b）所示。原始风场和精细化后的风场风速变化趋势、凹凸程度一致，但后者风速信息更丰富，为后续的湍流预警提供数据支撑。

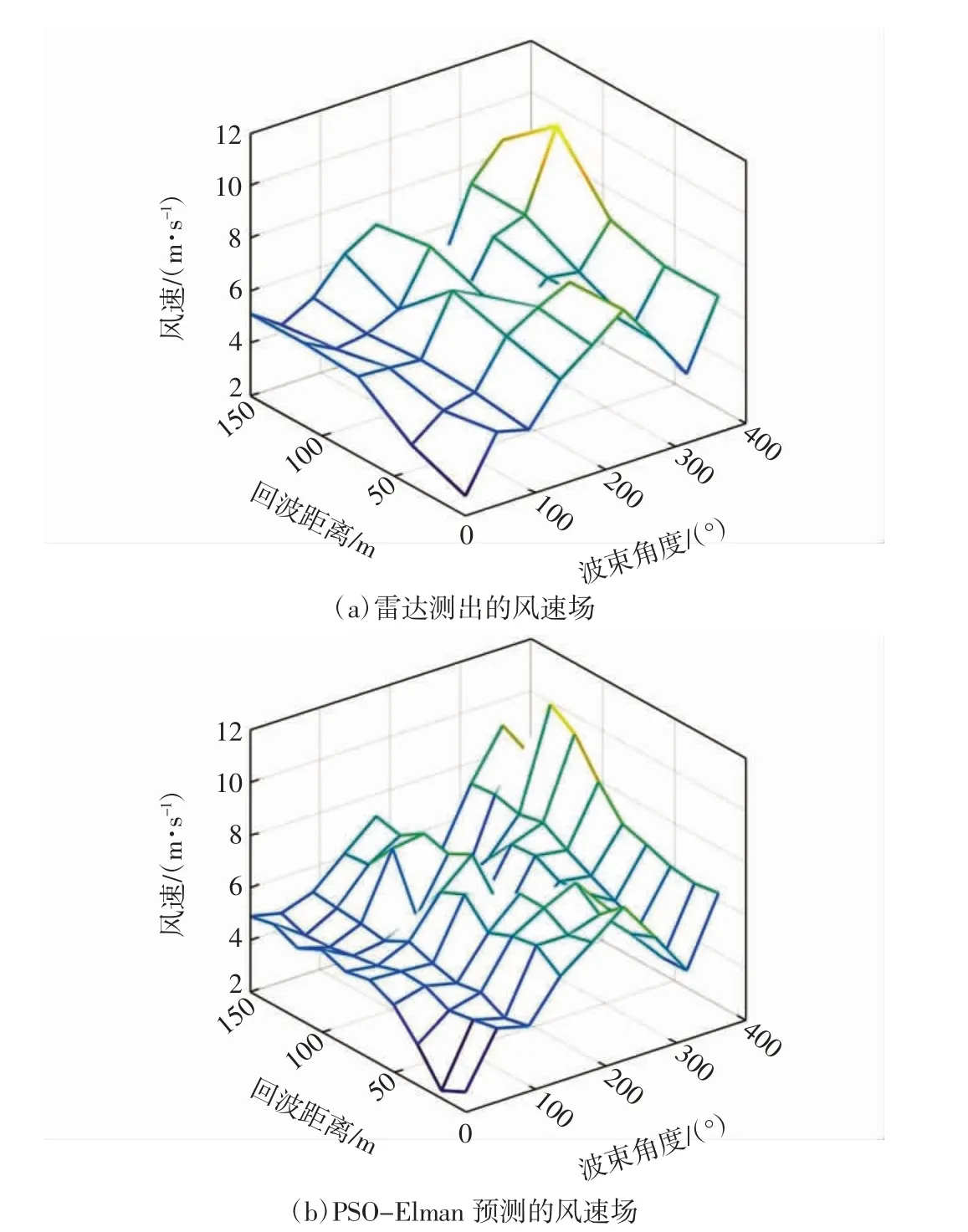
图7 风速精细化反演示意Fig.7 Inversion diagram of wind speed refinement

由于激光雷达的技术参数限制，导致现有数据不足。根据谱宽、信噪比、径向风速拟合出每个预测点的值，实现对验证数据的扩展，将扩展后的验证数据输入预测模型中，其结果如图8 所示。

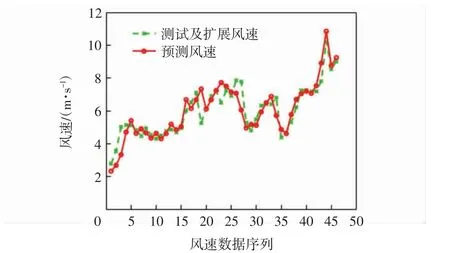
图8 测量及扩展与预测风速对比Fig.8 Comparison of measured and extended wind speed with predicted wind speed

结果表明，测量及扩展风速与预测风速之间的平均相对误差为6%。尽管测试集中的风速有突变的情况，但该模型能够有效地预测出相对于测量误差较小的风速，验证了算法的精度与有效性。

将激光雷达测量风速与本文算法预测出的风速进行线性回归分析，如图9 所示。

图9 预测风速与真实风速线性回归分析Fig.9 Linear regression analysis of predicted wind speed and true wind speed

从图9 中可看出，二者的回归曲线、散点图的趋势近似一致，相关系数为0.919，表明预测和测量的风速之间关联性较强，决定系数为0.842，表明网络对真实风场能拟合至84%左右，证明了由算法得出的权值、阈值更符合实际要求，泛化与映射能力强，预测的结果较为精确。

4 结语

本文建立了一种基于PSO-Elman 神经网络的激光雷达径向风速预测模型。此模型预测出风速与测量及扩展风速的相对误差为6%，激光雷达所测与预测的风速间的相关系数达到了0.919。表明该模型预测风速和测量风速相关度较高，误差较小，预测精度较高，训练后的模型与实际风场贴合程度较高，进而一定程度上提高了风场的网格密度和激光雷达的测风分辨率，实现了为湍流预警提供精细化风场数据的目的。