基于SelBagging算法的CFM56-7B发动机故障诊断
2022-02-27曹惠玲成宝荣
曹惠玲,成宝荣
(中国民航大学航空工程学院,天津 300300)
发动机作为飞机的重要组成部件,其工作环境恶劣,经常发生各种故障,严重时会影响飞机的安全可靠运行[1]。由于航空发动机的复杂性,单一的故障诊断方法会存在误诊和漏诊的情况,如何有效提高现有智能诊断方法的准确率已成为研究重点[2],因此对于集成学习的研究受到越来越多的关注。但集成学习也存在固有缺点,如通过生成多个基学习器来提高整体的泛化性能会增加程序的运行时间和空间消耗;另一方面,集成模型中泛化性能差的基学习器会影响整个集成系统的泛化性能[3]。针对以上集成学习的缺点,文献[4]提出了选择性集成,其思想是通过筛选出更少的基学习器进行集成,获得相同甚至泛化性能更强的集成效果,降低程序的运行时间和空间消耗。
针对如何对个体学习器进行选择,学者们提出了很多有代表性的方法。文献[5]通过遗传算法对选择过程进行优化,但个体学习器差异性的存在使得优化的搜索空间变得十分庞大,导致算法的运算时间过长。文献[6]通过剔除最差的基学习器来对集成进行层次修剪,虽大幅提高了算法的运行时间,但未考虑个体学习器间差异性的影响,只是缩短了程序运行时间,算法性能的提高并不明显。针对集成学习在选择阶段需要独立设置验证集而损失一定训练数据的缺点,文献[7]提出了一种快速剪枝选择集成算法,将基学习器个体评估融入原始数据本身,获得了集成运行时间上的优势,该算法和单独设置验证集的快速剪枝选择集成算法相比在正确率上有明显提高,但在部分数据集上的表现仍逊于传统Bagging 算法。因此,本文以排序法为基础,同时考虑基学习器的表现和差异性,结合Bagging 算法,提出SelBagging 算法,并建立多分类的SelBagging 发动机故障诊断模型,以期将该方法用于航空发动机的故障诊断中,提高诊断准确率。
1 基学习算法的选择
集成学习一般分为两个步骤[8]:①生成多个有差异性的基学习器;②使用某种方法对各基学习器分类结果进行合成。Bagging 算法主要用来产生有差异的Bootstrap 子集,基学习器主要对各种分类算法进行数据挖掘,因此,需要先选择基学习器所用的基学习算法。对于本文所用的Bagging 算法,其常用的基学习算法有决策树、神经网络等,因此,本文选择决策树和神经网络两种算法进行改进Bagging 算法的研究。
Cart 算法是决策树的一种[9],其对训练集的变化比较敏感,采用基尼(Gini)系数最小化准则来进行特征选择。假设样本集为D,Ck是属于第k(k=1,2,…,N)类的样本子集,|Ck|为第k个类别的样本数量,|D|表示数据集的数量,pk表示第k个类别的概率,则概率分布的基尼系数定义为
假设使用特征A将数据集D划分为D1和D2两部分,那么特征A的基尼系数为
当以决策树作为Bagging 算法的基学习器时,无需对决策树进行剪枝处理[10]。
神经网络处理单元可分为3 类:输入单元、输出单元和隐单元。设输入层节点数为n,隐层节点数为g,输出层节点数为m,wik为第i个输入层节点到第k个隐层节点的权值,vkj为第k个隐层节点到第j个输出层节点的权值,θk、γj分别为第k个隐层节点和第j个输出层节点的阈值,f1、f2分别为隐层、输出层的激活函数,则输入X=(x1,x2,…,xn)T,输出Y=(y1,y2,…,ym)T,隐层输出为Z=(z1,z2,…,zg)T,那么隐层第k个节点的输出为
输出层第j个节点的输出为
样本的网络期望输出yj与真实输出dj的误差函数为
式中e为误差向量。
神经网络模型的主要缺点是易陷入局部极小,而该特性对神经网络集成泛化能力的提高却起到了重要作用[10],这是因为如果各神经网络互不相关,则在学习中会陷入不同的局部极小,从而增加了集成的差异度,减小了泛化误差。
以上两种算法中,决策树学习能力强、训练快,但易陷入过拟合状态,常用于搜索排序中;神经网络可实现任何复杂非线性映射的功能,但收敛速度慢、计算量大且易收敛到局部最优,常用于图像处理中。由于两种算法各有优缺点,后续将结合实际数据对这两种算法进行进一步对比。
2 Bagging 算法
Bagging 算法是并行式集成学习方法最著名的代表[11],在给定包含N个样本点的数据集中,进行有放回的重采样过程。由式(6)可知对每个基学习器,训练时原始训练集中约有36.8%的样本未被使用,以此构造基学习器有差异的输入。
通过对样本子集分别采用相同的算法进行训练获得相应的基学习器,最后将这些基学习器结合得到强学习器[12],即Bagging 算法模型,如图1 所示。
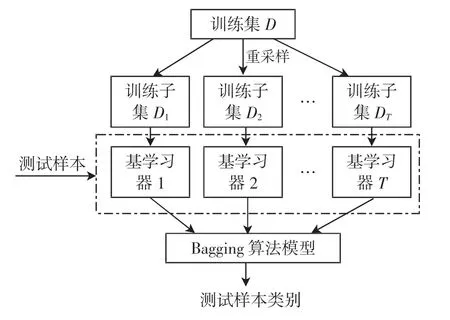
图1 Bagging 算法流程图Fig.1 Flow chart of Bagging algorithm
Bagging 算法的另一个重要步骤是模型融合。通常采用相对多数投票法来聚合多个模型。投票的目的是结合多个基学习器的输出从r个类别标记{c1,c2,…,cr}中得到最终类别,对于基学习器集合{h1,h2,…,hT}中的任意ht,其输出结果为一个r维的标记向量(ht1(x),ht2(x),…,htr(x))T,对于示例x,htb(x)∈{0,1}为基学习器ht在类别标记cb上的预测输出,若ht预测类别为cb,则ht=1。此时的集成输出标记可表示为
Bagging 算法特别适用于大规模集成场景,当Bagging 算法应用在小样本集上时,可通过重复计算来提升小样本的精度,这对故障数据较少的设备来说,是一种建立故障诊断模型的好方法。Bagging 算法也有不足,如训练时会产生表现差且冗余的基学习器这一现象及无法确定合适的集成规模等。由于集成差的基学习器及集成错误率相关的基学习器会降低Bagging算法模型的性能表现,所以本文对Bagging 算法模型进行改进研究,提出SelBagging 算法模型。
3 SelBagging 算法
通过第2 节的分析,实际的Bagging 算法中存在表现差且冗余的基学习器,这些基学习器不利于集成效果的提升,并且会占用过多的储存空间,所以需对训练出的基学习器集合进行筛选。选择的目的是通过某种度量准则选出差异度大且准确率高的基学习器子集进行集成(这里“差异度”定义为“对新的样本,各基学习器做出不同错误的趋势”)。
将选择性集成方法中的排序法作为传统Bagging算法的改进方法,排序法通过某种度量标准对基学习器集合进行评价并排序,然后在排序后的基学习器中按顺序选择一定比例的基学习器进行集成,排序法的一个关键问题是集成模型中基学习器个数的选择,采取固定保留个数的基学习器;对于排序法,恰当的排序标准是关键,模型性能的“好”可使用分类准确率代替,但个体学习器间多样性的度量方法有很多,本算法选用文献[10]中的KW(Kohavi-Wolpert)方差作为评估分类器集成多样性的度量指标。考虑一个分类器模型,y 是h 要预测的类别,则KW 方差公式为
式中:zj(j = 1,2,…,N)为N 个样例中的第j 个样例;l(zj)为对zj正确分类的分类器的数目;T 为总的分类器数目。当所有的分类器都给出相同的分类结果时,KW=0,该集成系统的多样性程度最低;当有一半的分类器正确分类、一半的分类器错误分类时,KW=0.25,集成系统的多样性程度最高。确定了集成多样性的评估标准后,SelBagging 算法步骤如图2 所示。
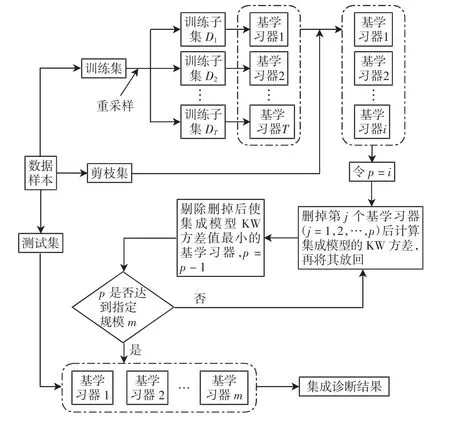
图2 SelBagging 算法流程图Fig.2 Flow chart of SelBagging algorithm
具体步骤为:①首先通过Bagging 算法在训练集上构造多个Bootstrap 子集,在这些子集上使用同种算法训练出对应的基学习器,在剪枝集上计算这些基学习器的分类准确率;②将这些基学习器按准确率进行排序,保留前i 个基学习器作为排序法的初步筛选结果;③对剩余基学习器依次去除掉每个基学习器,并在计算此时集成模型的KW 方差后将其放回;④剔除删掉后使集成模型KW 方差值最小的基学习器,判断剩余基学习器个数是否达到指定规模m,如未达到则返回步骤③,否则进行下一步;⑤通过相对多数投票法对剩余基学习器子集投票。对每个新样例点x,使用相对多数投票法的集成诊断结果为
式中:m 为最终集成规模,ht(x)为每个基学习器上的结果。
4 基于SelBagging 算法的应用
发动机指印图是在对以往发动机故障诊断经验总结和大量故障数据统计分析的基础上建立起来的发动机小偏差量的样条图(见图3),在发动机气路故障诊断方面具有较高的准确性。
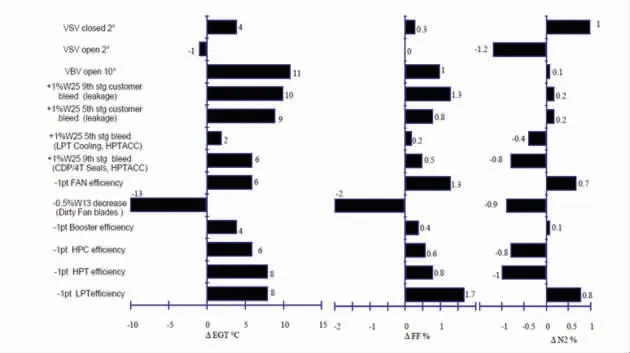
图3 CFM56-7B 发动机指印图Fig.3 Fingerprint map of CFM56-7B engine
本文采用文献[13]中的比值系数法与文献[14]中的单位向量法作为指印图数据的处理方法,对指印图处理后的数据如表1 所示,比值系数法中两列值分别为ΔEGT/ΔN2、ΔFF/ΔN2;单位向量法中3 列值分别为、。其中:ΔEGT 为发动机排气温度变化量;ΔFF 为燃油流量变化量;ΔN2 为发动机高压转子转速变化量。

表1 比值系数法与单位向量法故障标识Tab.1 Fault identification of ratio coefficient method and unit vector method
由于实际的发动机性能参数偏差量会因测量、读取和计算等过程的存在而产生各种误差,所以为了提高数据的覆盖范围,需对处理后的数据进行扩充加噪,这里按照原数据的分布规律添加一定程度的高斯白噪声以增加模型的鲁棒性。
需注意的是在加噪时应添加与自身数据呈一定比例的偏差。此处扩充数据量为2 160 个,其中1 300个实例作为训练集,430 个实例作为剪枝集,430 个实例作为测试集。图4 分别展示了两种数据处理方法下,在1 300 个实例上使用10 交叉验证得到的噪声幅值对单个决策树、单个神经网络分类准确率的影响。其中决策树的特征选择标准为Gini 系数,决策树最大深度及其他参数采用默认值,固定随机状态参数的值;神经网络中采用Relu 函数,并使用两个隐层,每个隐层包含100 个单元,alpha 设置为0.001,其他参数默认,同样固定随机状态参数的值。
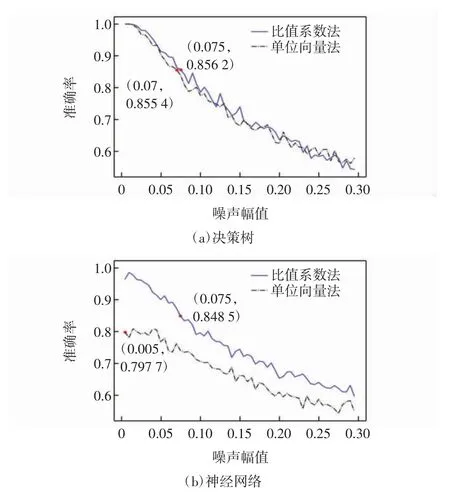
图4 不同算法下噪声幅值对准确率的影响Fig.4 The influence of noise amplitude on accuracy under different algorithms
在加噪过程中,添加噪声过大可能使某些故障类型的数据相似度过大,更加难以区分;添加噪声过小虽然能得到较好的分类模型,但模型的泛化能力可能会大打折扣,考虑到后续建模时集成模型对基学习器的改善效果,选取使基学习器分类精度达到0.85 附近时的噪声幅值。由图4 可知,数据处理方法不同,适宜添加噪声的幅值也不同,在单位向量法处理的数据上使用神经网络算法,无论噪声添加得多小,其诊断效果依然不理想,所以不采用这种组合。表2 展示了保留的3 种分类算法和数据处理方法的组合以及在不同组合下适宜添加的噪声幅值,并计算了对应组合的分类准确率和训练时间。
表2 中,组合1 代表在通过比值系数法处理指印图数据后添加0.075 噪声幅值扩充的数据集上使用决策树算法训练的模型,以下依此类推。
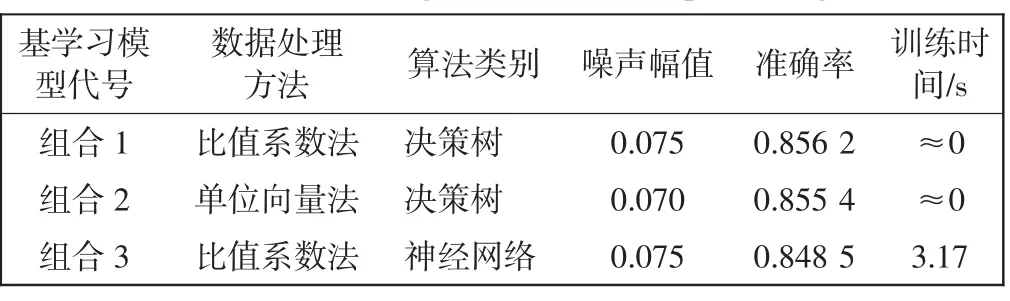
表2 不同算法与数据处理方法组合适宜添加的噪声幅值Tab.2 The noise amplitude suitable to be added under the combination of different algorithms and data processing methods
为讨论基学习器个数对集成的影响,在已获取基学习算法及数据来源的基础上,固定随机种子数,决策树和神经网络的拓扑参数与表2 中单个模型的拓扑参数相同,使基学习算法在不同的Bootstrap 子集上进行充分训练,得到不同组合下基学习器个数对传统Bagging 算法模型的影响,如图5 所示。
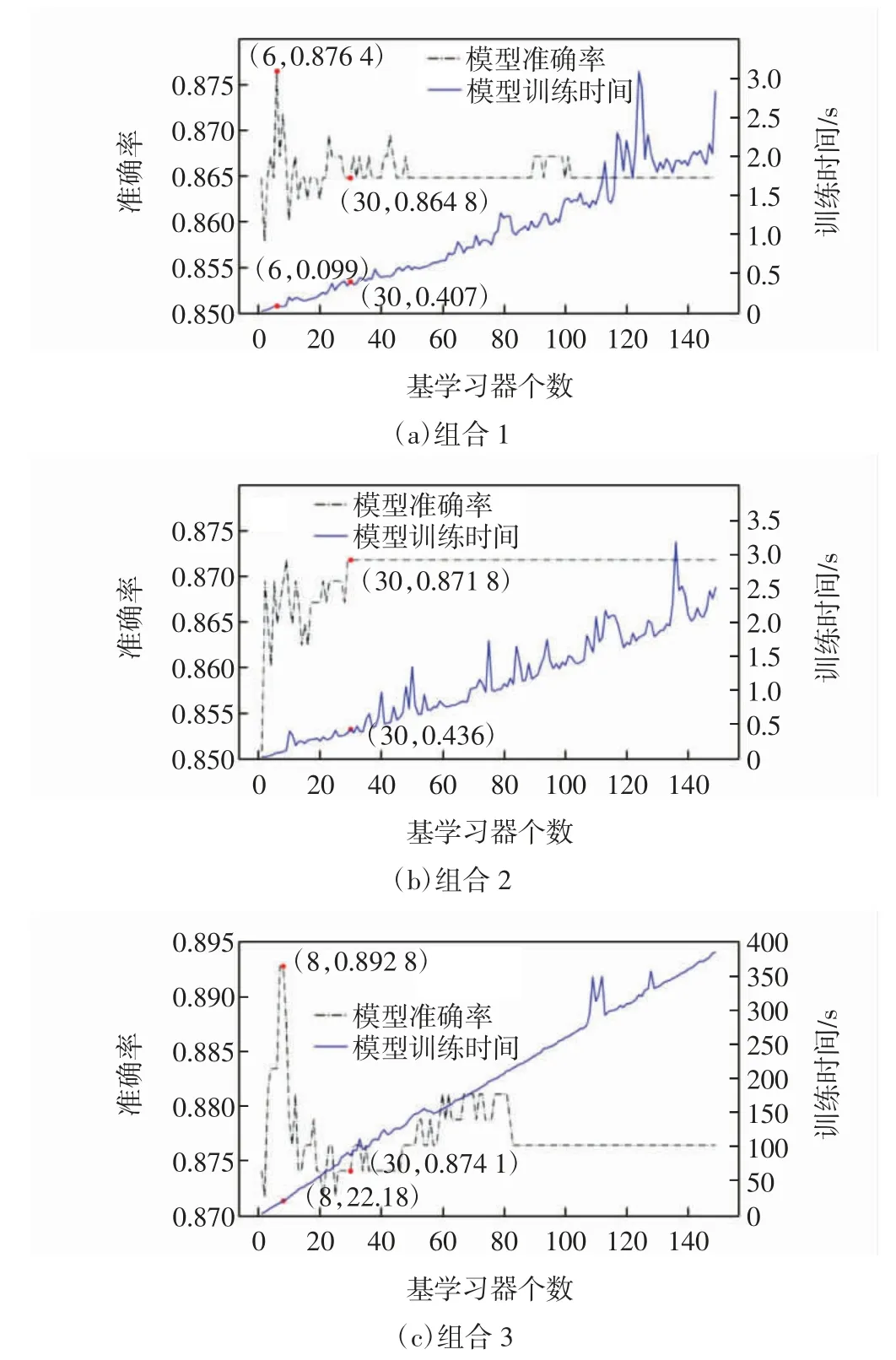
图5 不同组合下基学习器个数对Bagging 算法模型的影响Fig.5 The influence of the number of base learners on the Bagging algorithm under the different combination
由图5 可看出:集成模型的训练时间几乎与基学习器个数呈正比;但并不是基学习器个数越多准确率越高,基学习器个数在一定范围内会对集成模型的准确率产生影响,当个数增加到一定值时,集成模型的准确率趋于稳定,这是因为后面训练的基学习器和某些已完成训练的基学习器过于相似,并不能对集成模型的性能产生有益影响;以决策树作为基学习器比以神经网络作为基学习器的集成模型训练时间少的多,可以看到当集成规模增大时,决策树算法的这种优势将进一步加大;另外,最佳的基学习器个数并不是一个定值,基学习器个数不同甚至可以得到分类性能相当的集成模型。
以上讨论了数据处理方法、算法类别、噪声幅值及基学习器个数对集成的影响,下面依据第3 节Sel-Bagging 算法,进行选择性集成运算。在进行选择性集成之前,首先确定初始基学习器个数T=500,由图5可知,3 种组合方式下的基学习器个数在30 以内时,集成模型准确率的波动较大,当个数大于30 时,基学习器个数的增加对集成效果的增益并不是很大,故设置初步保留规模i=30。初步选择后,剩余基学习器个数越少,剔除过程所用的时间将会越多。表3 对比了3种组合方式下,传统Bagging 算法模型(基学习器个数为500)和SelBagging 算法模型在最终集成规模为10、15、20 时的分类准确率及响应时间。
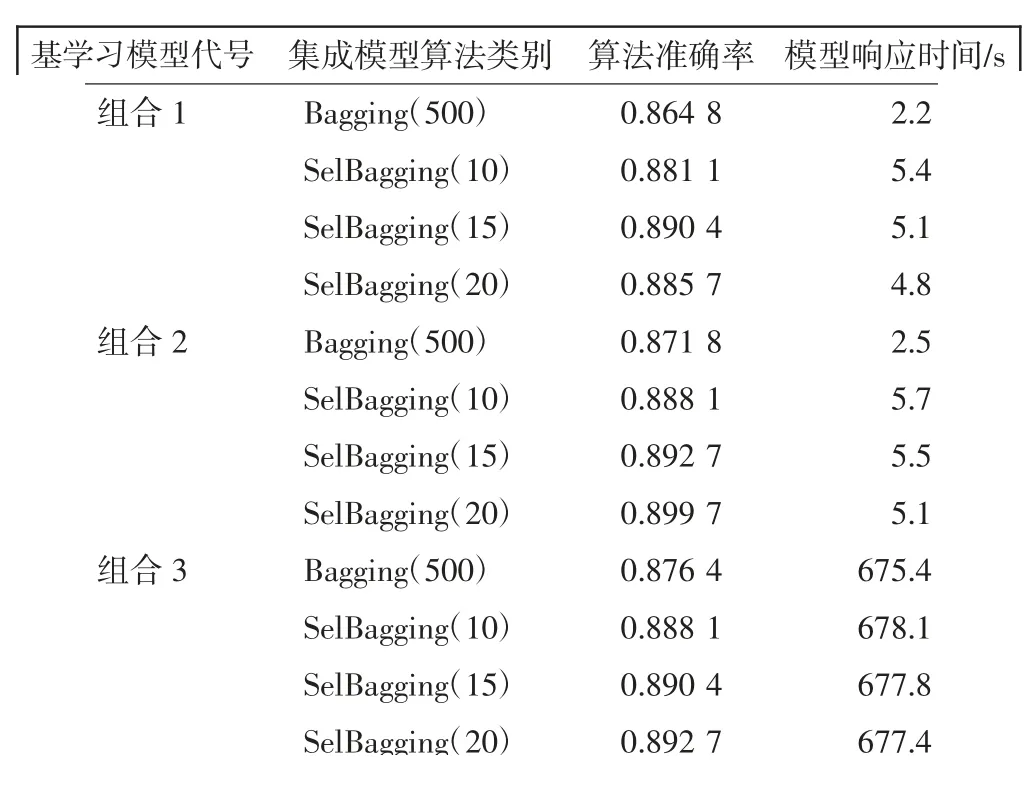
表3 Bagging 算法与SelBagging 算法性能对比Tab.3 Comparison of performance between Bagging algorithm and SelBagging algorithm
由表3 可见,经过选择性集成后,本文提出的Sel-Bagging 算法相较传统Bagging 算法在3 种组合方式上都有较大的性能提高;而选择过程所用的时间并未像预想中的那样长,甚至与训练多个决策树所用的时间相差无几;综合时间和性能考虑,如在实际应用中需要根据故障数据做即时的训练并诊断时,使用决策树作为基学习器算法能够在相对较短的时间内做出较为理想的诊断决策。若不考虑训练时间,神经网络作为基学习器算法也能取得较好的集成效果。
以一个航空发动机故障案例对SelBagging 算法进行实际应用的检验。由航空公司某起发动机状态不正常的故障案例,通过监控软件获取发动机主要性能参数值,参考文献[12]计算得到该故障下发动机性能参数小偏差量:ΔEGT=15 ℃,ΔFF=1.62%,ΔN2=-0.95%。将偏差量输入SelBagging 诊断模型中,在组合1 上设置模型的最终集成规模为15,组合2、组合3 上设置模型最终集成规模为20,得到诊断结果为:在3 种组合方式上建立的发动机故障诊断模型都能将该发动机故障参数偏差量诊断为表1 中的第12 类故障,对应的故障类别为-1pt HPT efficiency,即高压涡轮间隙控制阀门故障。后续飞机排故表明该故障是由于高压涡轮间隙控制活门失效导致的高压涡轮组件性能损失。
由此可见,3 种组合下建立的SelBagging 诊断模型在实际应用中都能给出较好的诊断结果,在实际使用中也可以将3 种集成模型都用来进行故障诊断,并对3 种集成模型的输出再进行投票,以进一步提高诊断的准确率。
5 结语
航空发动机的故障诊断对于其维修及安全运行具有重要意义,为提高发动机故障的诊断准确率,本文通过对传统的Bagging 算法进行改进,提出了SelBagging 算法,并得到以下结论:①数据处理方法及数据噪声的幅值都会对模型准确率以及泛化能力有影响,在实际中应进行合理斟酌;②某些情况下(如基学习器个数不同时),传统Bagging 算法并非一定能大幅提高集成模型的分类准确率,而通过排序法及差异性度量指标进行选择性集成,剔除掉基学习器子集中表现差且冗余的基学习器通常可以使模型的集成效果得到较为理想的改善;③实际应用中,建立的多个集成模型依然可以使用投票法进行集成;④不同的集成模型有不同的最佳基学习器个数,在应用中,通过绘制基学习器个数对集成的影响图来寻找最佳集成规模进行模型的融合通常不实际,而对选择性集成来说,该问题可以通过筛选找到1 组分类性能好且有足够差异性的基学习器子集,使该子集的集成逼近甚至超越最佳基学器个数子集的集成来解决。
