基于应变率变化的爆破块度预测模型及应用
2022-02-23翟小鹏陈占扬陈忠辉
翟小鹏,杨 军,陈占扬,汤 宇,陈忠辉
(1.北京理工大学爆炸科学与技术国家重点实验室,北京 100081; 2.北京奥信化工科技发展有限责任公司,北京 100040)
岩石在高速冲击、爆炸等动态载荷的作用下会碎成很多小块,该过程是一个复杂的物理过程,块度尺寸不仅与岩石的性质有关,与载荷的加载方式也有很大关系。
在爆破实践活动中,影响块度的因素有很多,主要包括爆破参数和岩体性质两方面。已有大量的学者对爆破破岩机理和工程应用开展了相关研究,提出了很多的块度预测模型。根据模型的假设条件和理论基础,可以分为应力波模型、经验函数模型、能量模型、分形理论模型和神经网络模型五类。应力波模型是根据应力波在岩体中的传播规律,以不同的破岩理论为依据对爆破过程进行分析,计算单元应力状态,并将其应用于爆破块度预测。应力波模型主要包括:HARRIES模型[1]、BMMC模型[2]、BCM模型[3]、能流分布模型[4],该类模型的特点是能够对爆破过程进行定量的计算,但普遍将岩体假设为均质材料,不考虑岩体构造的影响,计算结果与实际爆破结果往往存在较大的差异。经验函数模型是以函数形式表示爆破块度的总体分布情况,可以全面了解产物的破碎程度。常见的分布函数模型有:KUZ-RAM模型[5]、BOND-RAM模型[6]、别兹马特类赫模型[7],该类模型建立了爆破参数与爆破块度的关系,计算简便、快捷,但计算精度普遍较低。能量理论模型以破碎功理论为基础,提出爆破块度预测的经验公式。能量理论模型主要有: GAMA模型[8]、JUST模型[9]等,该类模型需要进行大量大爆破试验来确定相关参数,而且计算精度较低。分形理论模型认为岩石内部的断裂形状具有自相似性,局部裂纹的扩展即可得到岩体整体的破碎形态,建立了分形维与爆破块度的关系[10-11],但该方法还不成熟,在爆破领域使用较少。神经网络模型将影响块度的因素进行整合简化,通过机器学习来获得块度分布相关参数[12-13],该类模型块度预测准确,但由于神经元网络基于风险最小化原则,所以容易出现训练速度慢、过拟合等理论上难以解决的问题[14]。同时,神经网络模型的应用需要大量的数据样本作为支撑,也影响了它的使用和推广。
在爆破块度预测方面,已经有很多包含了台阶爆破参数的经验和半经验模型,但大多数参数均为爆破参数,即使考虑到岩体性质也只是给出岩石试件的力学参数,并不能全面反映岩体的性质。爆破块度主要是由岩体内部的构造裂隙扩张产生的,岩体构造才是控制爆破块度的主要因素[11]。因此,建立一种能够反映岩体整体性质的块度预测模型,对矿山生产有着重要意义。
1 理论计算
1.1 应变率-块度分布模型
目前学界普遍认为,岩石的动态断裂是材料内部微裂纹的扩张和传播的造成的。Grady等[15-16]通过对岩石的动态破碎过程进行了研究,认为岩石破碎后的尺寸与应变率存在指数关系,并得出以下计算公式:
(1)
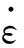
Grady等[15-16]给出的断裂模型指示岩石的断裂的块度尺寸与应变率相关,且与应变率的-2/3次方成正比。即岩石在高应变率加载的情况下,碎裂的块度与应变率存在指数关系。相关学者也进行了大量的研究,结果表明岩石的断裂尺寸和应变率存在指数关系[17-18]。因此,岩石爆破破碎的块度可以参考此结论建立模型。
在爆破作业中,爆区块度由炮孔近区至远区依次增大,而应变率是依次减小。因此,对于露天台阶爆破块度分布规律,可以建立一种基于应变率变化的块度分布的模型,函数表达式为
(2)
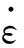
通过这种方式可以将块度预测模型推广到更广泛的工况当中,来解决实际工程中的块度预测问题。p、q为该块度预测模型中的核心参数,在不同的工程条件下,这两个参数只对特定的爆破对象具有一定的精度。因此,需要根据不同的工况来确定参数。
1.2 炮孔近区应变率变化规律
一般而言,炮孔近区指的是30~50倍孔径范围内的岩体[19]。由于爆炸作用高强度冲击波及高温、高压气体的作用,在炮孔近区很难测得应变率的变化规律。因此,利用柱面波协调方程,引入柱坐标下径向应变率与振动速度参数的表达式[20]:
(3)
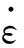
由式(3)可知,若已知爆炸作用下炮孔近区各点峰值速度的径向衰减规律,便可求得该点应变率的值。依据波动理论,柱坐标系下应力波在介质中的传播同时满足质量及动量方程:
ρ0D=ρ1(D-v1)
(4)
P1=ρ0Dv1
(5)
式中:D为冲击波波速,m/s;P1为扰动岩体内部的压力值,kPa;ρ0、ρ1分别为扰动前后岩体密度,kg/m3;v1为扰动岩体的质点速度,m/s。
由Hugoniot方程可知,岩石中冲击波传播速度与质点的振动速度具有如下关系[21]:
D=a+bv
(6)
式中:a、b为与岩石力学性质有关的参数;a与声波在岩石内传播的速度基本相同,m/s;b的取值范围为1.0~1.5。
由于露天台阶爆破一般情况下为耦合装药,因此,爆生气体只有等熵膨胀状态,炮孔壁的压力值为[22]
(7)
式中:pr0为炮孔壁的压力峰值;ρe为炸药密度;D为炸药爆速;k为绝热指数,一般取k=3;n为冲击波碰撞压力增大倍数,n=8~11,取n=8。
联立式(4)~式(7)可得炮孔壁初始质点最大振动速度:
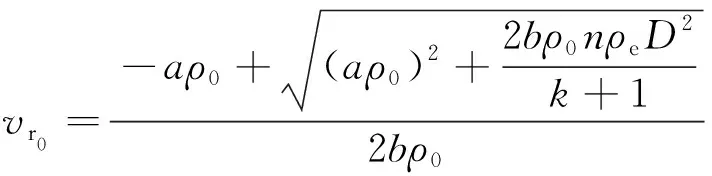
(8)
式中:vr0为炮孔壁质点最大振动速度;ρ0为扰动前岩体密度;其余参数同前。
对于冲击波及应力波的传播与衰减问题,通常采用指数函数来表示[23]:
(9)
(10)
式中:σr为柱坐标系下距离炮孔中心r处的压力峰值;νr为距离炮孔中心为r处的质点速度;α为冲击波或应力波衰减指数,α的取值为1.5~3.0;r0为炮孔半径;r为质点距离炮孔中心的距离。
由式(10),质点振动速度随径向距离的增大呈指数型衰减,对式(10)求偏倒数近似求得柱坐标系下炮孔近区岩体应变率的计算公式:
(11)

由式(11)可以看出,炮孔近区的应变率随距离的增加呈指数衰减,衰减速率不仅与炸药的特性有关,与岩体性质也有很大的关系。台阶爆破过程中,近区岩体的径向应变率值大于环向应变率,所以采用较大的径向应变率表征质点的应变率。该公式能够给出炮孔近区不同范围内应变率的解析解,这对于解决炮孔附近块体破碎的块度预测问题有着重要意义。
1.3 爆孔近区块度分布规律
在露天台阶爆破过程中,影响爆破块度的因素有很多,其中最重要的就是台阶爆破参数与岩体性质。爆破设计的各项参数容易获得,而矿山岩体的地质条件变化颇大,岩体内部存在大量性质不同、产状各异的裂隙,不仅影响着岩体力学性质,也影响着岩体破坏形式。相关研究表明,对于节理发育的岩体,岩体构造才是影响爆破块度的主控因素。即在合理的爆破参数下,岩体的性质对块度的最终分布起着决定性的作用。
在工程实践过程中,通常是爆破后通过筛分或图像分析的方式对岩块大小进行统计分析,得出块度分布规律,进而评价爆破效果的优劣。在爆破施工前,一般是通过经验公式对块度进行预测,该方法简洁高效,但存在很大误差。相同的爆破参数,不同的岩石的爆破效果千差万别。因此,建立一种与岩体性质相关的块度预测模型,对于快速高效地对露天台阶爆破进行预测,指导矿山实际生产有着重要意义。
建立炮孔近区的块度分布模型,实现对爆破近区的块度预测。将式(11)代入式(1)得出炮孔近区块度分布函数:
y=
(12)
式中:y为炮孔半径r处块度的大小;p、q为相关系数,其取值与岩体结构特性相关(包括各种结构面、弱面的分布情况及弱面的充填物性质)。其余参数同前。
式(12)中除p、q外,所有参数都容易获得。而p、q的取值往往只对特定的对象具有较高的精度,并不具有广泛的适用性,在不同的工程条件下需要单独考虑。在爆破参数固定的情况下,影响p、q取值的最主要因素便是岩体组成、结构特性。因此,对于指定矿山,只要针对某种岩体提取爆后块度信息,即可很方便地获取p、q,从而对该种岩体的爆后块度进行预测。
2 工程应用
湖山铀矿位于纳米比亚Erongo地区的纳米布沙漠,西部毗邻大西洋,矿区距离科普斯瓦蒙德镇约60 km,与ROSSING铀矿相邻。湖山铀矿是世界开采规模最大的铀矿,年开采剥离量1.4亿t,年处理矿石1 500万t,设计年产量6 800 t U3O8,矿区总体储量可以满足20台百万千瓦级核电机组近40年的天然铀需求,主要为中广核集团在国内运营的核电站提供铀原料。
地质工程师尝试对当地已有的地层单元进行详细划分,建立以岩性为标识的细分地质模型,但由于岩性组合复杂多变,未能实现这一目标。现场的地质情况很复杂,每个地层都不同的层序,各地层之间接触关系纷杂,部分地区褶皱发育,覆盖层最大厚度大15 m。湖山铀矿地层及岩性如表1所示。
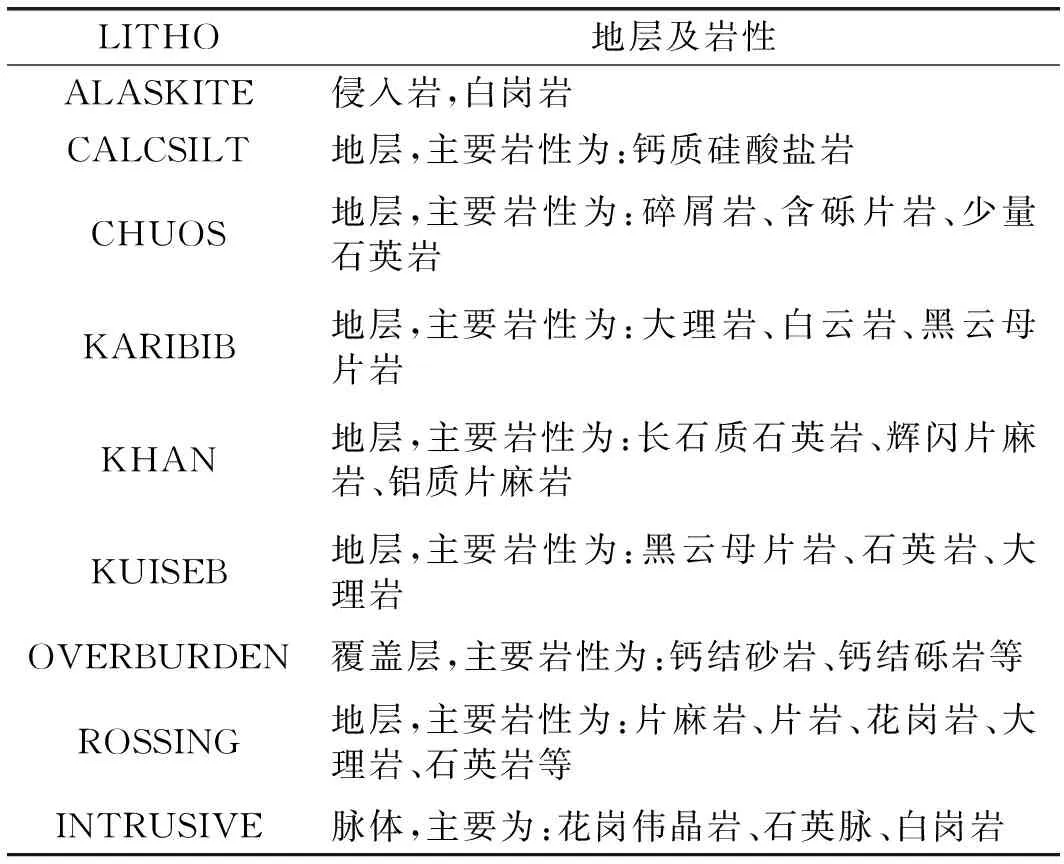
表1 湖山矿地层及岩性
湖山铀矿共包含CALCSILT、CHUOS、KARIBIB、KHAN、KUISEB、ROSSING 6个地层,侵入岩为白岗岩,脉体为花岗伟晶岩、白岗岩和石英岩。
以2号坑1期的2B31D015台阶为例,对露天台阶爆破块度预测方法进行验证。台阶位2号坑1期,坡底标高为15 m,台阶长度83 m,宽度为35 m,共有炮孔126个。2B31D015台阶岩性主要为白岗岩。2B31D015台阶的爆破设计参数、白岗岩及炸药参数分别如表2、表3所示。将相关参数代入式(12),得:
(13)
式中:y为岩块尺寸,m;r为距离炮孔中心距离,m;p、q为与岩体结构相关的参数。
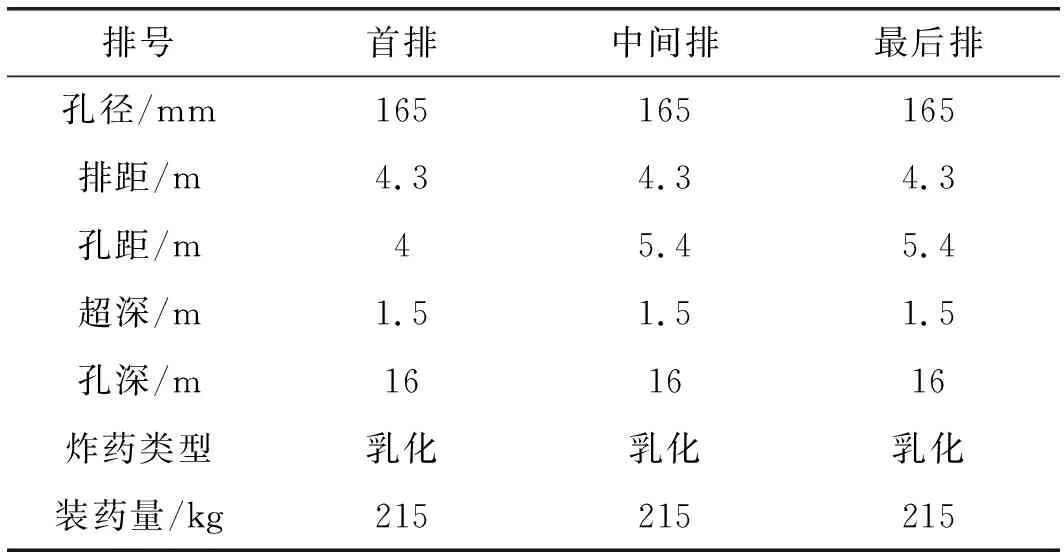
表2 2B31D015爆破设计参数
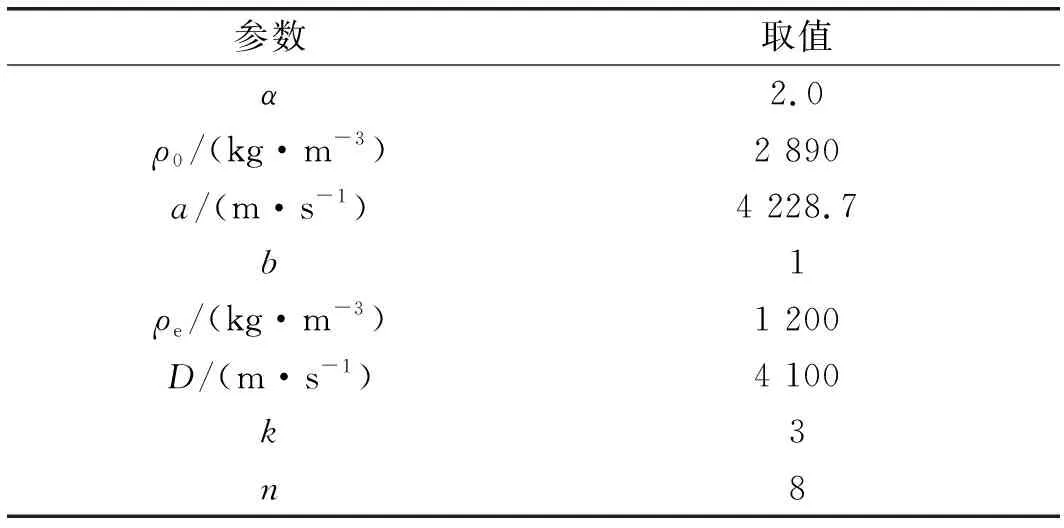
表3 白岗岩及炸药参数
单孔负担体积V=a(孔距)×b(排距)×H(台阶高度),2B31D015台阶a=5.4,b=4.3;根据单孔负担体积计算不同尺寸岩块所占累积比例:
(14)
式中:F为块度累积百分比,x为岩块尺寸,m。
2号坑1期的2B31D009、2B31D010、2B31D012、2B31D013、2B31D014台阶均为白岗岩,而且爆破设计参数相同。对上述5个爆区的爆破后的不同阶段的开挖面设置参照物,并进行图像拍摄。最后利用Split-desktop 4.0软件对爆破的块度进行分析,得出各台阶的块度分布曲线,利用数据回归的方式得出式(14)中参数p=0.98,q=—1.334 8,将p、q代入式(14)得出在白岗岩的块度分布特征函数:
F=1.025x0.499,x≤0.952 5
(15)
式(15)即为白岗岩在表2、表3的爆破参数下的块度预测公式。当爆破参数发生改变时,将调整后的参数代入式(12)中重新计算公式,即可得出新的块度预测公式。将p、q的值代入到式(12)中即可得到炮孔近区块度分布的规律。即可得出在表2、表3的爆破参数下白岗岩炮孔近区的块度分布公式:
y=0.172r4.004 4,x≤30r0
(16)
台阶实测孔位坐标如图1所示,虚线标记处为一自由面,其他三面夹制。爆区采用乳化炸药现场混装车进行装药,孔内管、地表管均为ORICA公司生产,起爆弹为SASOL公司生产的Pentolite型起爆弹。地表管孔间延时42 ms,排间延时100 ms。起爆网路如图2所示。

图1 2B31D015台阶实测孔位坐标Fig.1 Hole coordinates ofbench 2B31D015
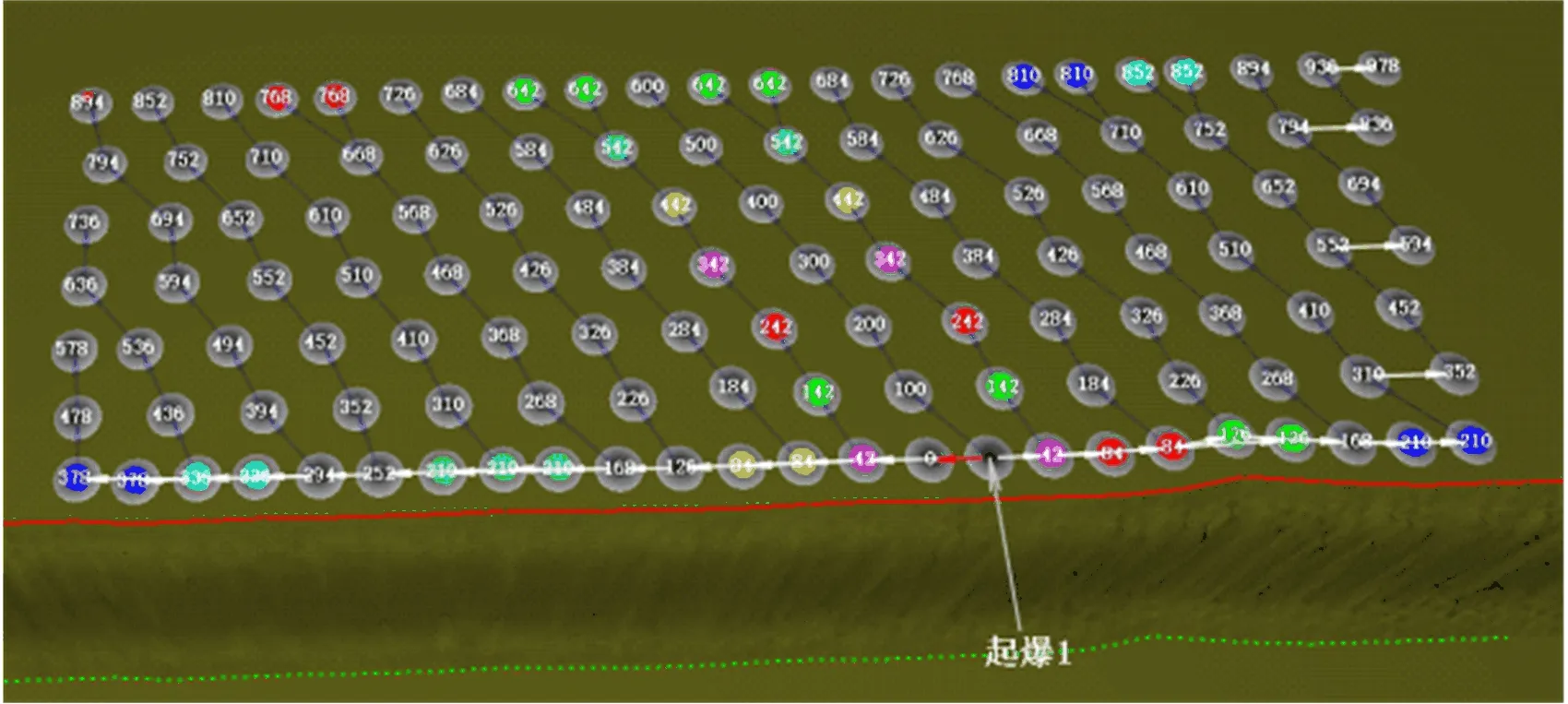
图2 2B31D015台阶爆破网路Fig.2 Firing circuit of bench 2B31D015
2B31D015台阶爆破后,以直径25 cm的篮球作为标记物,对不同时间的8个开挖面拍摄。利用Split-desktop 4.0对图像进行块度分析(见图3),其中蓝色表示岩块之间界线,红色表示岩粉,淡绿色为不分析区域(岩墙、地面等)。

图3 块度分析Fig.3 Block analysis
对块度分析结果进行统计分析,最终得出爆堆的块度整体分布数据和曲线。2B31D015台阶的块度分布如图4所示。
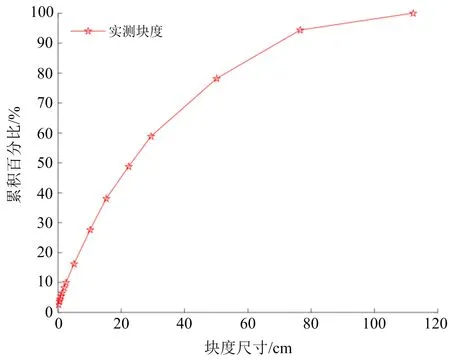
图4 2B31D015台阶的块度分布Fig.4 Fragmentation distribution curve of bench 2B31D015
利用式(15)白岗岩的块度预测公式绘制块度分布曲线,与现场统计的块度曲线进行对比,结果如图5所示。
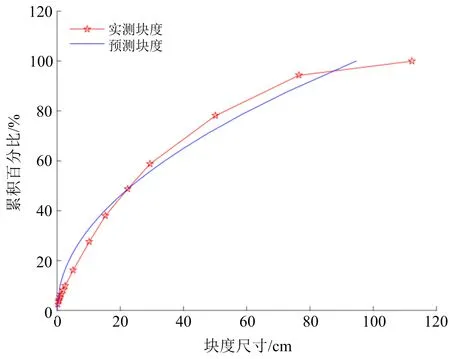
图5 2B31D015台阶实测与预测块度对比Fig.5 Comparison of measured and predicted Fragmentation size of bench 2B31D015
由图5可以看出,预测块度曲线与实测块度曲线趋势基本一致,能够反映爆破块度的分布特征。将块度预测值与实测值进行对比,分析预测误差(见表4)。结合图5与表4可知,F30及以下预测误差偏大;F40~F60有最高的预测精度,平均误差为8.1%;F70~F100也有较高的精度,平均误差为16.17%,预测结果与实测结果基本一致。总体而言,预测误差在工程可接受的范围内。
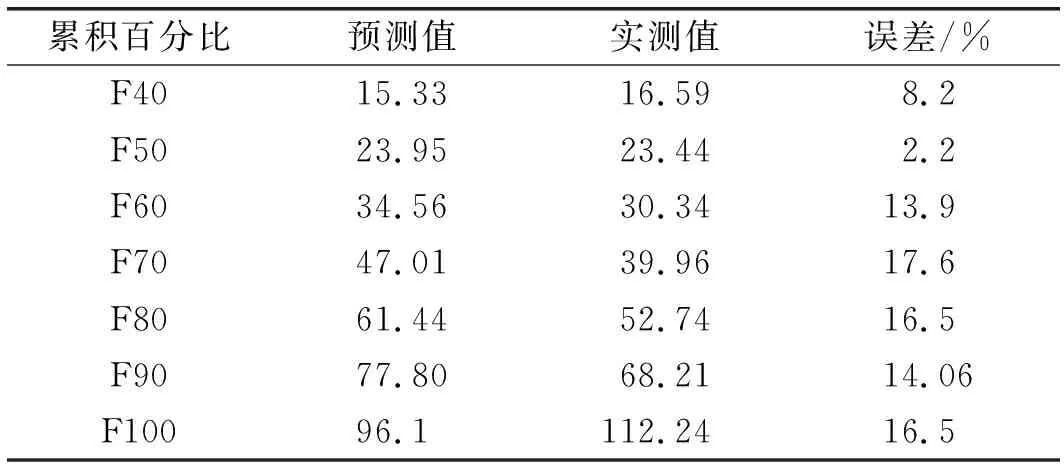
表4 块度预测误差分析
3 结论
1) 对现有的块度预测方法,根据模型的理论基础和假设条件,可以分为应力波模型、经验函数模型、能量模型、分形理论模型和神经网络模型。并对其优缺点进行了评述,认为岩体构造是控制爆破块度的主要因素。
2) 从理论上分析了炮孔近区应变率的变化规律,结合炮孔近区块度的分布函数,推导了应变率-块度的分布模型。对不同岩性的爆区,通过数据回归的方式获得了块度分布函数的相关参数。该函数考虑了岩体结构对爆破块度的影响,不仅能够对块度的整体分布进行预测,同时也能够定量计算炮孔近区不同范围内岩块的尺寸。
3) 针对现场爆破效果,采用对爆堆的不同开挖面进行拍照和图像分析的手段,得到实际的块度分布曲线。通过验证分析得知,基于应变率变化的块度预测模型的F50~F80的平均误差为12.5%,能够较为准确地预测爆破块度。
