爆破作用下含后缘裂隙岩质边坡的断裂力学分析

宋 娟，王 晋，胡 敏，贺龙喜

(邵阳学院城乡建设学院，湖南 邵阳 422000)

爆破开挖是目前岩质边坡施工最主要的手段之一。爆破产生强烈的冲击和振动作用，会造成边坡岩体的松动变形以及原生裂隙的张开。随着边坡向下延伸，频繁的爆破引起岩体损伤累积，这会使得岩体原生裂隙不断扩展并相互贯通，进而引发边坡滑坡。因此，探究爆破作用下岩质边坡的稳定性情况，揭示边坡岩体裂隙扩展规律，对于边坡工程的建设具有重要意义。

目前关于爆破作用下边坡失稳机理的 研究，已有大量研究成果。周子涵等[1]基于突变理论，揭示了爆破作用下边坡的失稳机制。王秀杰等[2]研究了锦屏一级水电站高边坡在爆破开挖作用下的失稳机理。王来贵等[3]分析了爆破作用下边坡岩体内应力场的调整规律。陈明等[4]深刻阐述了爆破作用下边坡岩体内裂隙扩展规律。吴新霞等[5]研究了爆破荷载作用下边坡稳定性控制方法。上述研究大多基于极限平衡法理论，在一些工程问题中的计算结果往往误差较大。近几十年来，随着断裂力学的不断发展，其越来越广泛的应用于分析边坡滑坡问题[6-7]。王栋等[8]运用断裂力学相关理论推导了含后缘裂隙岩质边坡在重力和裂隙水压共同作用下的稳定性计算公式。ZHANG等[9]基于断裂力学将复合应力强度因子与断裂韧性的比值定义为边坡安全系数。WU等[10]从断裂力学的角度出发研究了不同后缘裂隙长度边坡的破坏模式演变规律。

综上研究，目前关于爆破作用下岩质边坡失稳破坏机制的研究成果颇为丰富[11-14]，但鲜有从断裂力学角度出发探究爆破作用下岩质边坡失稳破坏机理的研究。基于此，本文利用断裂力学相关理论，推导了爆破作用下岩质边坡后缘裂隙尖端复合应力强度因子计算公式，进一步将裂隙尖端应力强度因子与边坡岩体的断裂韧度的比定义为边坡稳定性系数，分析了结构面几何参数对边坡稳定性的影响和裂隙扩展方向变化规律，最后通过现场实例进行验证。

1 爆破作用下边坡后缘裂隙扩展的力学模型

边坡岩体裂隙的形成和发展是内外动力耦合作用的结果。复杂的地质构造运动和外界荷载的扰动作用使的在边坡坡顶形成深度不一的张裂隙，工程上称后缘裂隙[3]，同时在边坡前缘会形成近水平或缓倾坡外的裂隙，中间未破坏区域对边坡稳定性具有控制作用。频繁的爆破开挖作用会进一步加剧边坡后缘裂隙的发展，边坡滑坡的发生往往是这些后缘裂隙不断扩展与坡体下部近水平或缓倾坡外的裂隙贯通所引发。

边坡岩体裂隙构造复杂，且呈现空间分布。因此，在三维空间内很难利用理论分析方法来研究爆破作用对裂隙的扩展影响。本次研究将三维裂隙简化为二维平面应变问题来处理(见图1)。一岩质边坡中存在一条长度为z的张开型后缘裂隙，受到滑体自重应力在裂隙表面产生的法向应力σn和切向应力τn的作用，且裂隙面与水平方向的夹角为α，同时并受到爆炸应力波SV(P)波的作用。

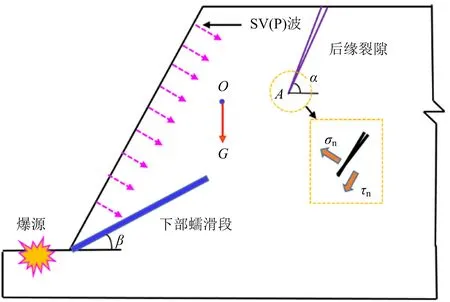
注：O为滑体重心位置；A为边坡后缘裂隙尖端；G为滑体重力，kg；α为后缘裂隙与水平方向的夹角,°；β为下部裂隙与水平方向的夹角，°。图1 边坡后缘裂隙扩展的计算模型Fig.1 Calculation model of crack propagation at the back edge of slope

根据应力强度因子叠加原理，线弹性范围内，多个荷载作用下裂隙尖端应力强度因子等于各单个荷载作用下裂隙尖端应力强度因子之和。因此。受爆炸应力波和滑体自重共同作用下边坡后缘裂隙尖端应力强度因子等于爆破荷载产生的动态应力强度因子和滑体自重产生的静态应力强度因子之和：

KS=K动+K静

(1)

式中：KS为考虑爆破作用后缘裂隙尖端总的应力强度因子，MPa/m1/2；K动为爆炸应力波作用下后缘裂隙尖端应力强度因子，MPa/m1/2；K静为滑体自重作用下后缘裂隙尖端应力强度因子，MPa/m1/2。

1.1 爆炸应力波对边坡后缘裂隙扩展的影响

在实际爆破工程现场，爆炸应力波通常为柱面波，为实际应用可行而将问题简化处理为平面波，爆炸应力波在岩体中传播的主要为弹性P波和SV波。根据文献[15]的研究结果可知，P波和SV传到岩体裂隙表面时，不仅在裂隙尖端产生I型动态应力强度因子，而且产生II型动态应力强度因子。

本次研究主要探讨爆炸应力波在裂隙面上产生的剪切破坏，剪切破坏主要受裂隙尖端II型应力强度因子控制，SV波产生的II型应力强度因子在同等强度下是最大的，因此下文主要对SV波进行研究。这里令：

m=ω/c

式中：ω为SV波的圆频率，Hz；c为波速，m/s；m为波数，具有1/长度的量纲。

爆破应力波-SV波在裂隙尖端产生的应力强度因子为[15]：

(2)

其中

τm=μm2ψ0

(3)

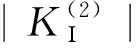
1.2 滑体自重对边坡后缘裂隙扩展的影响

边坡滑动概化力学模型如图2所示，O为滑体重心位置；A为边坡后缘裂隙尖端；α为后缘裂隙与水平方向的夹角,°；β为下部裂隙与水平方向的夹角，°；G为滑体重量，kg；M为滑体自重在裂隙尖端产生的弯矩，kN/m；h为平均高度，m；a为重心到裂隙尖端的水平距离，m；b为裂隙尖端到重心的垂直距离，m；z为后缘裂隙的长度，m。

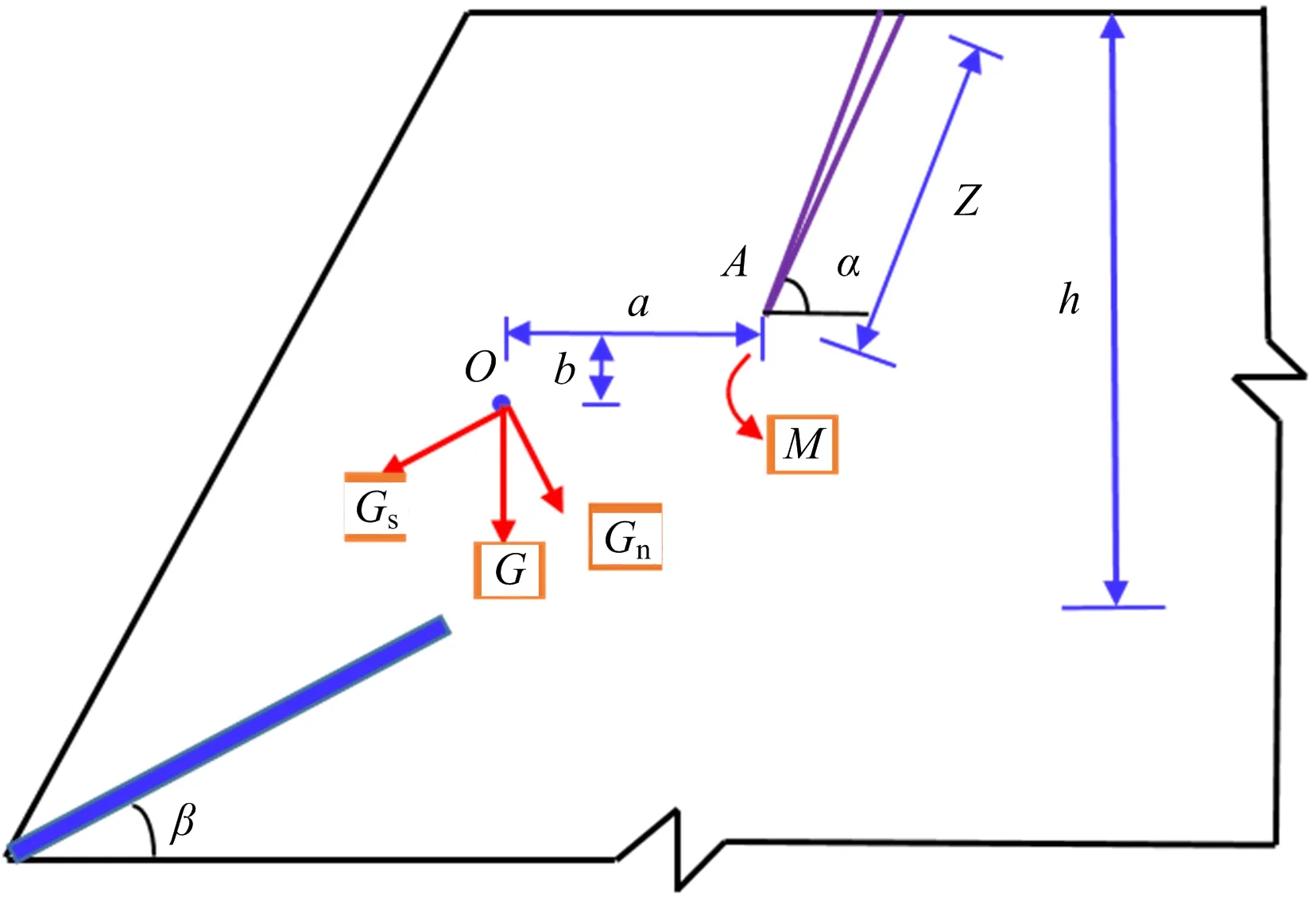
图2 边坡概化力学模型Fig.2 Generalized mechanical model of slope

定义滑体重力G在下部裂隙平行方向产生的力为Gs，滑体重力G在垂直于下部裂隙方向产生的力为Gn，进一步将其分解为沿后缘裂隙的切向力Gτ和法向力Gσ，各个力的具体表达式为

Gs=Gsinβ

(4)

Gn=Gcosβ

(5)

Gτ=Gscos(α-β)+Gnsin(α-β)

(6)

Gσ=Gssin(α-β)-Gncos(α-β)

(7)

G=γV

(8)

式中：Gs为作用于下部裂隙的蠕滑力，kN；Gn为作用于下部裂隙的剪切力，kN；Gσ为作用于后缘裂隙面上的法向力，kN；Gτ为作用于后缘裂隙面上的切向力,kN；γ为岩体容重，kN/m3；V为单位长度滑体体积,m3。

边坡裂隙概化模型，边坡滑体中心O在后缘裂隙尖端A产生的力矩M为

M=Ga

(9)

边坡后缘裂隙扩展的断裂力学模型如图3所示，根据应力强度叠加原理可将滑体自重作用下裂隙扩展模型受力状态分解为①～③，分别为拉应力、剪应力和弯矩，各自受力状态下的裂隙尖端应力强度因子为

(10)

(11)

(12)

(13)

(14)

(15)

图3 裂隙尖端应力强度因子叠加原理Fig.3 Superposition principle of stress intensity factor at crack tip

式中：KΙ1为滑体自重作用下后缘裂隙面上拉应力在裂隙尖端产生的I型应力强度因子，MPa/m1/2；KΙΙ1为滑体自重作用下后缘裂隙面上剪应力在裂隙尖端产生的II型应力强度因子，MPa/m1/2；KΙ2为滑体中心在后缘裂隙尖端弯矩产生的I型应力强度因子，MPa/m1/2；σ为滑体自重在裂隙面上产生的拉应力，MPa；τ为滑体自重在裂隙面上产生的剪应力，MPa；σmax为弯矩裂隙面上产生的最大拉应力，MPa。其他参数同前。

因此，对于边坡后缘张拉裂隙在滑体自重作用下的应力强度因子可表示为

(16)

式中：KΙ静为滑体自重作用下后缘裂隙尖端产生的I型应力强度因子，MPa/m1/2；KΙΙ静为滑体自重作用下后缘裂隙尖端产生的II型应力强度因子，MPa/m1/2。

将式(4)～(15)代入式(16)可求得边坡后缘张拉裂隙在滑体自重作用下的应力强度因子：

(17)

将式(2)和(16)代入式(17)可求得考虑爆破作用边坡后缘张拉裂隙尖端总的应力强度因子：

(18)

2 边坡稳定性分析

边坡后缘裂隙受滑体自重和爆破荷载的共同作用，可分解为沿裂隙的剪切应力和垂直裂隙的拉应力，可简化为拉剪裂隙扩展模型(见图4)，属于Ⅰ-Ⅱ复合型断裂模型，，裂隙尖端极坐标应力分量表达式为[16]

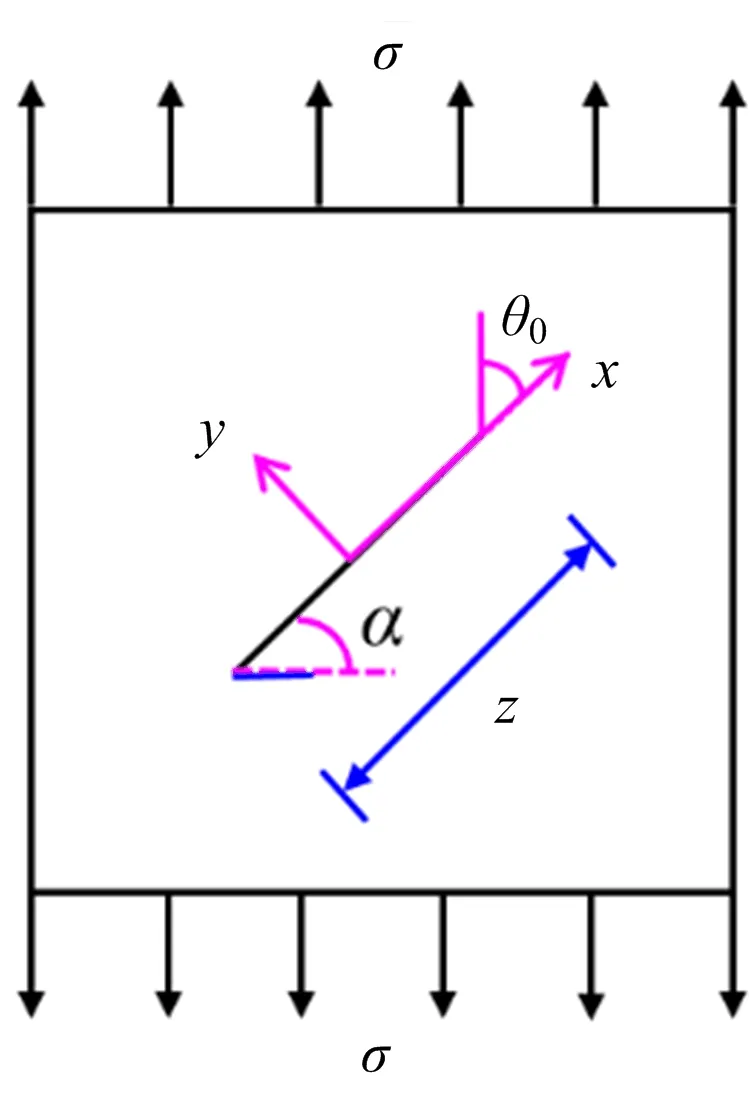
图4 拉剪裂隙扩展模型Fig.4 The model of tension-shear crack propagation

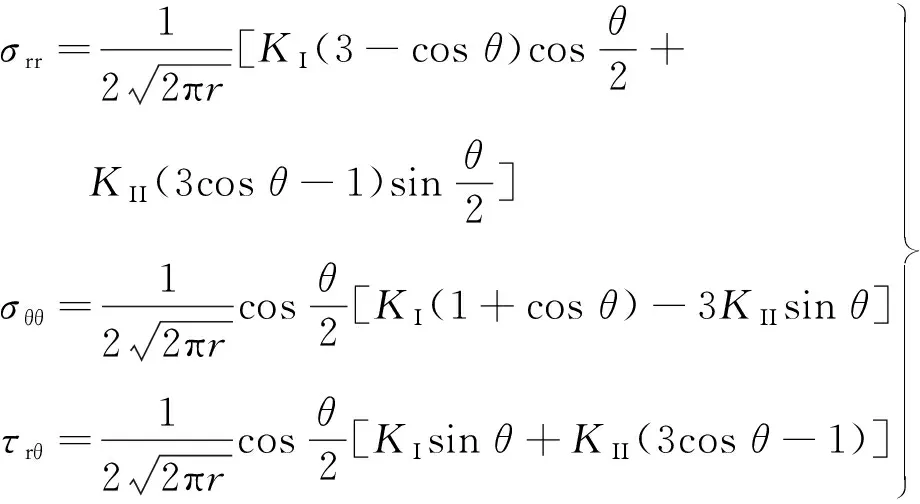
(19)

式中：σrr为径向应力，MPa；σθθ为轴向应力，MPa；τrθ为剪切应力，MPa；θ为裂隙尖端裂隙扩展方向，°；r为裂隙尖端到裂隙上任一点的距离，m；KΙ为裂隙尖端Ⅰ型应力强度因子，MPa/m1/2；KΙΙ为裂隙尖端Ⅱ型应力强度因子，MPa/m1/2。

根据最大轴向拉应力准则，Ⅰ-Ⅱ复合型裂隙会沿着最大拉应力σθθmax的方向扩展，岩体裂隙尖端起裂角θ0满足方程[16]：

KΙsinθ0+KII(3cosθ0-1)=0

(20)

进一步可求得裂隙起裂角为

(21)

式中：θ0为裂隙尖端起裂角，°。

将式(18)代入式(21)便可求得考虑爆破作用时边坡后缘裂隙的起裂角。

边坡后缘裂隙处于拉剪应力状态下，边坡岩体的I型断裂韧性KΙc决定着裂隙是否起裂，岩石KΙc可通过室内力学实验测得。依据最大轴向应力准则，拉剪应力状态裂隙扩展可等效为纯I型裂隙，因此其复合应力强度因子KΙe可表示为：

(22)

将式(18)代入式(22)便可求得考虑爆破作用时边坡后缘裂隙复合应力强度因子KΙe：

(23)

依据断裂力学相关概念，定义边坡稳定性系数为考虑爆破作用时边坡后缘裂隙复合应力强度因子KΙe与岩石断裂韧性KΙc的比值，即：

FS=KΙc/KΙe

(24)

式中：FS为边坡稳定性系数；KΙe考虑爆破作用时边坡后缘裂隙复合应力强度因子，MPa/m-1/2；KΙc为岩石断裂韧性，MPa/m-1/2。

可通过FS的大小来判断边坡是否稳定。当FS<1时，裂隙开始起裂，伴随频繁爆破作用，边坡失稳；当FS>1时，裂隙不会起裂，边坡处于稳定状态；当FS=1时，边坡处于临界失稳状态。

3 边坡稳定性影响因素分析

前文求得了边坡在滑体自重和爆破荷载共同作用后缘裂隙尖端复合应力强度因子和裂隙起裂角的表达式，定义了边坡稳定性系数。边坡后缘裂隙角度对边坡稳定性和起裂角的影响如图5所示。从图5a可知，稳定性系数随后缘裂隙角度的增大先减小后增加，在裂隙角度在76°时稳定性系数达到最小值。从图5b可知，裂隙起裂角随后缘裂隙角度的增大而呈现非线性增大，这表明随着裂隙角度的变大，所形成滑面长度增加，裂隙越有利于向坡面方向扩展。起裂角的变化范围较大，表明裂隙角度对起裂角的影响较大。

图5 后缘裂隙角度对边坡的影响Fig.5 The influence of the angle of the back edge crack on the slope

边坡后缘裂隙长度对边坡稳定性和起裂角的影响如图6所示。从图6a可知，稳定性系数随裂隙角度的增大呈现非线性减小，这表明裂隙越长，边坡越容易失稳，和现场规律相一致。从图6b可知，裂隙起裂角随裂隙角度的变化而保持不变，这表明起裂与裂隙长度无关。

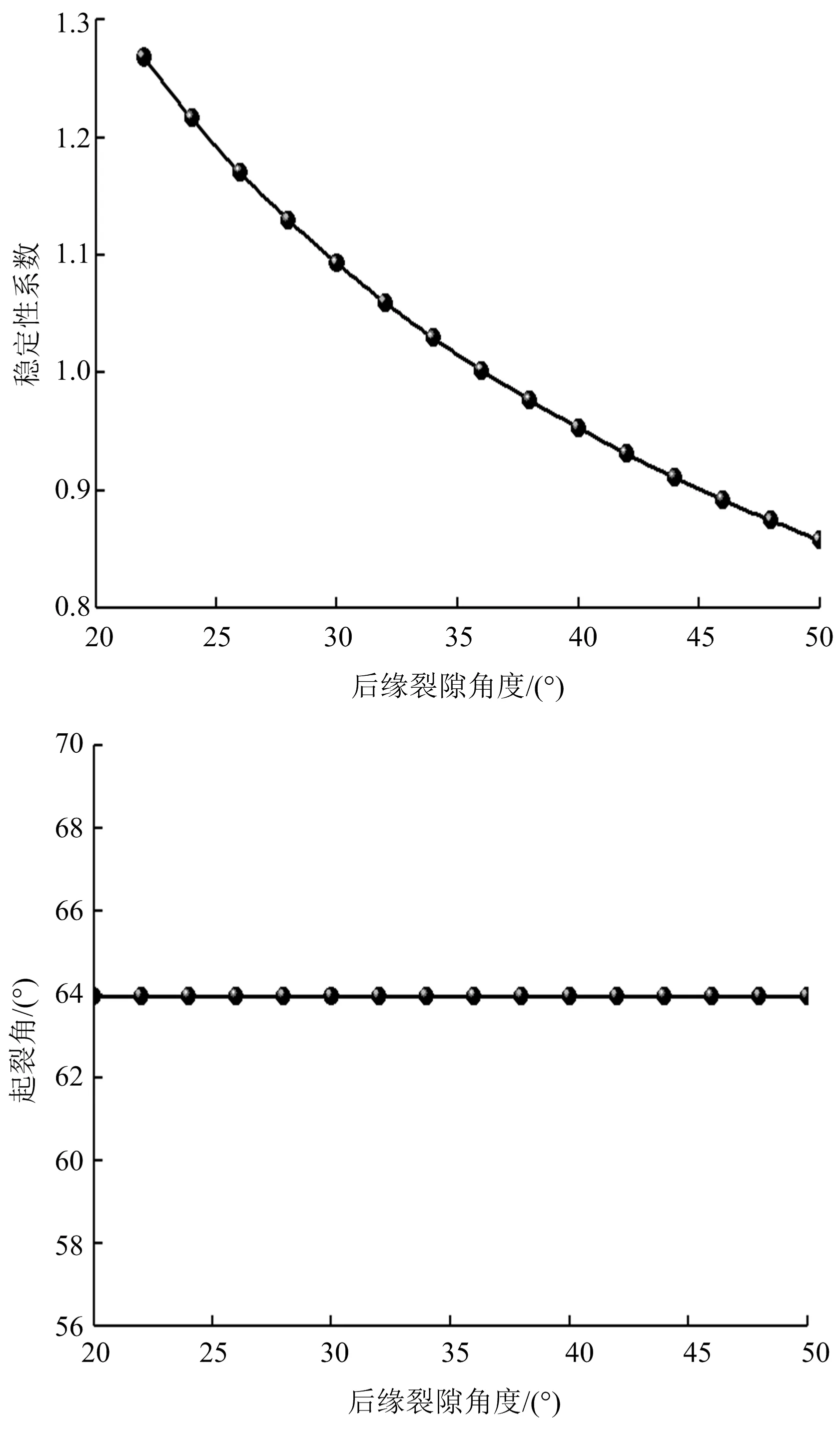
图6 后缘裂隙长度对边坡的影响Fig.6 The influence of the length of the back edge crack on the slope

边坡平均高度对边坡稳定性和起裂角的影响如图7所示。从图7a可知，稳定性系数随平均高度的增大先呈现线性增加，这表明平均高度越大，滑面越长，边坡越稳定。从图7b可知，裂隙起裂角随平均高度的增大呈线性减小，这表明平均高度越小，裂纹越来越趋向于坡面扩展，且滑面的长度较小。

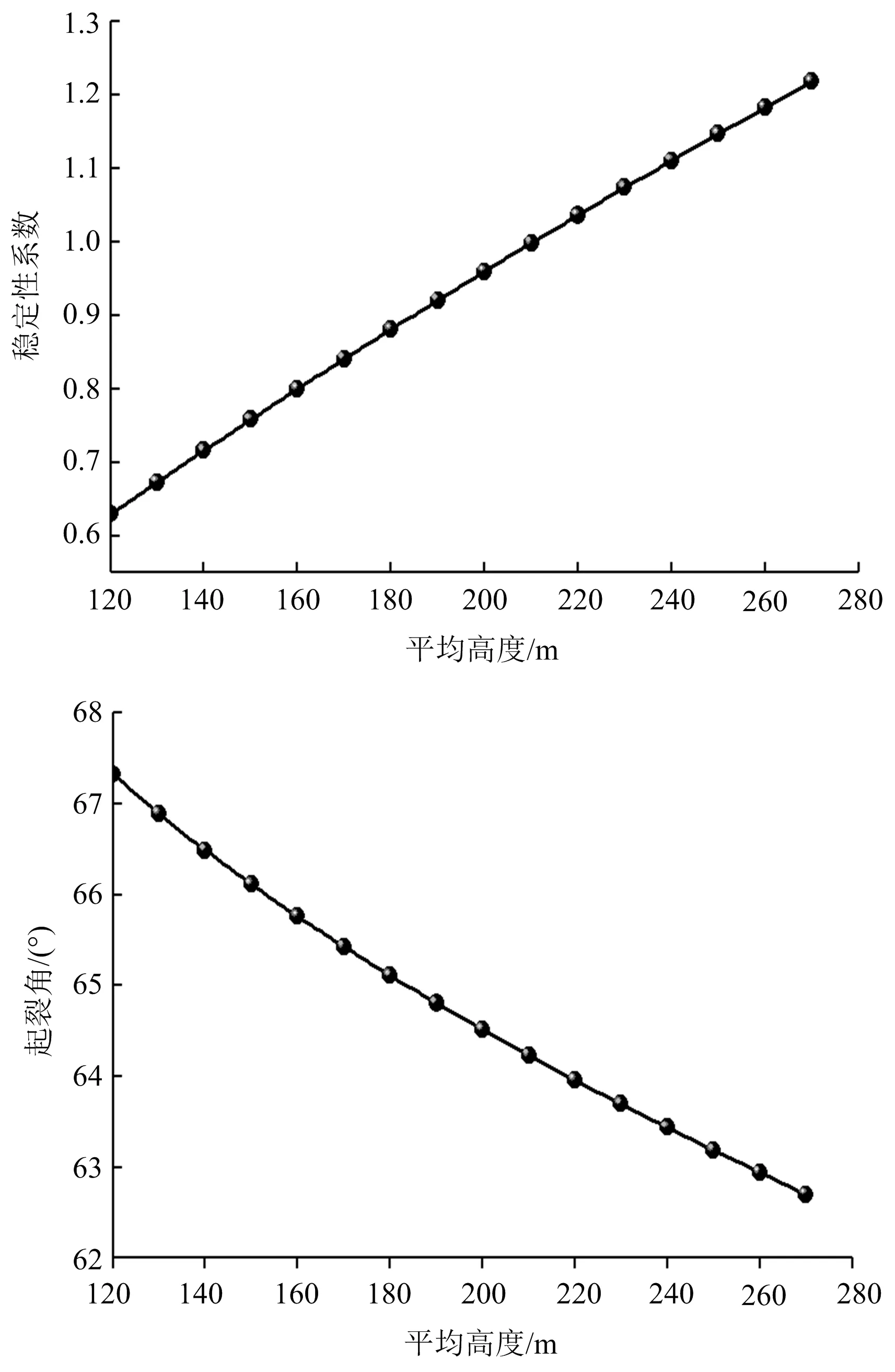
图7 平均高度对边坡的影响Fig.7 Influence of average height on slope

爆炸应力波的圆频率对边坡稳定性和起裂角的影响如图8所示。从图8a可知，稳定性系数随频率的增大先呈现线性减小趋势，这表明频率越大，边坡受爆破影响的程度越大，越容易失稳，这和现场实际相吻合。从图8b可知，裂隙起裂角随平均高度的增大呈线性减小，这表明平均高度越小，裂纹越来越趋向于坡面扩展，且滑面的长度较小。

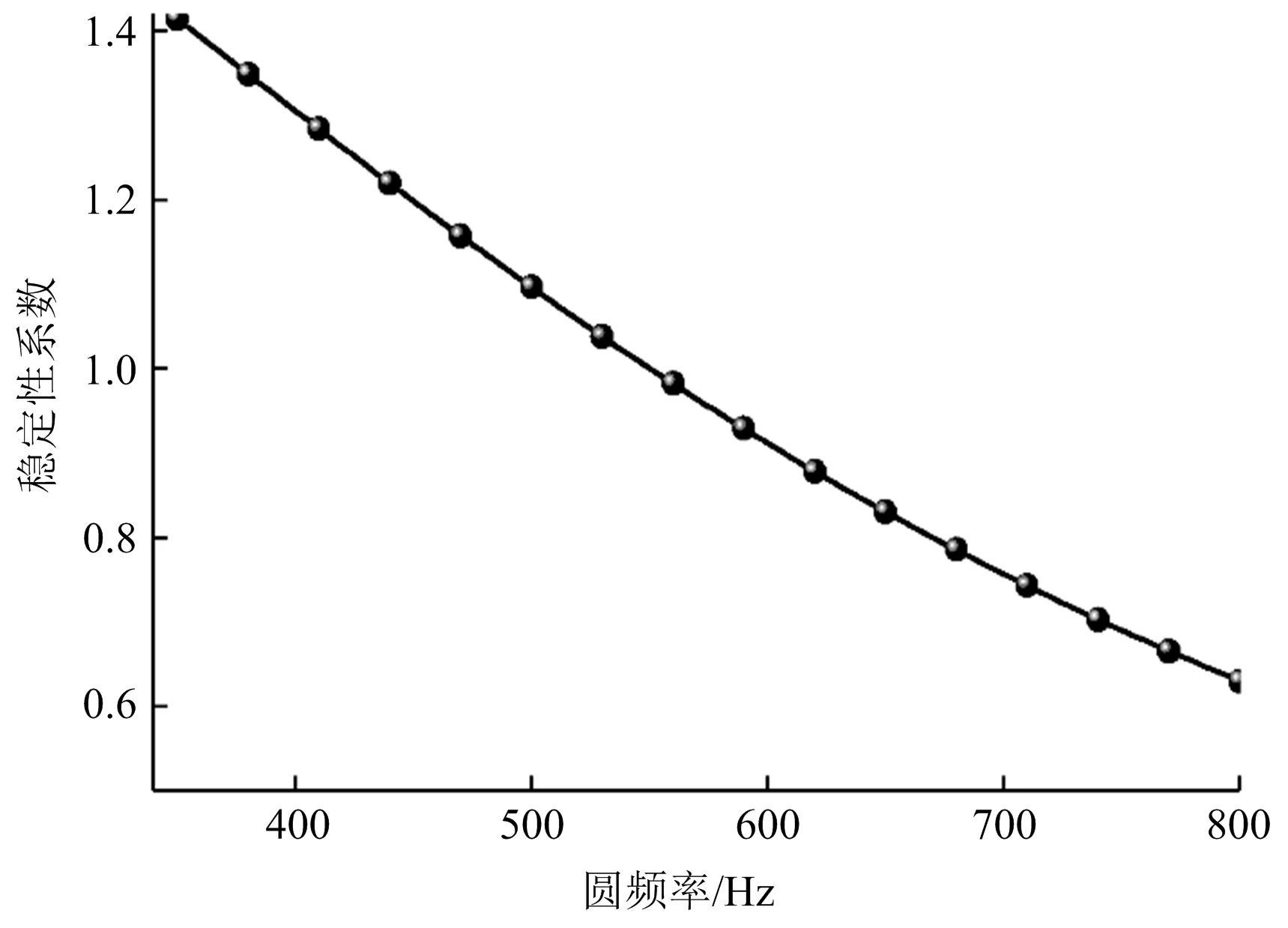
从上述分析结果可知，后缘裂隙几何参数和爆破参数不同，裂隙尖端复合应力强度因子不同，边坡稳定性系数和起裂角也不同。裂隙角度、裂隙长度、平均高度和爆破应力波频率对边坡稳定性系数和起裂角的影响不同。起裂角和边坡稳定性系数随裂隙倾角在40°～80°范围内的变化趋势相反，在80°～90°范围内的变化趋势相同；边坡稳定性系数随裂隙长度的增大而减小，裂隙长度对起裂角不产生影响；起裂角和边坡稳定性系数随平均高度的变化趋势相反；边坡稳定性系数和起裂角随爆破应力波的圆频率的变化趋势相同。

4 工程实列分析

为验证本理论在实际工程中的合理性，对一实际边坡进行分析。该实例为某露天矿西北帮一处局部滑坡区域，该滑坡区域倾向西南，最大坡角42°，边坡裂隙较为发育，岩体较为破碎，地质结构简单，岩性以混合岩为主，局部有裂隙较为发育的绿泥石英岩，频繁的爆破开挖和地质构造作用使得边坡后缘出现明显的裂隙(见图9)。滑坡区域前缘存在明显的蠕滑结构面，工程地质剖面及裂隙概化模型如图10所示。

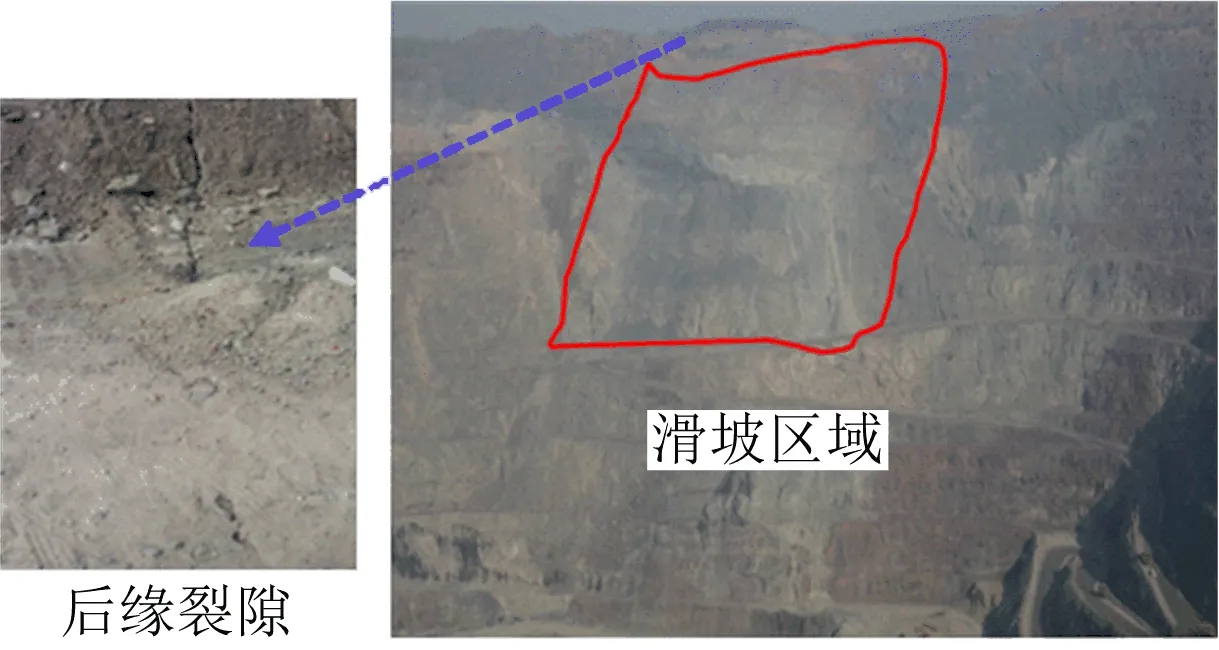
图9 边坡滑坡现状Fig.9 Current situation of slope landslide

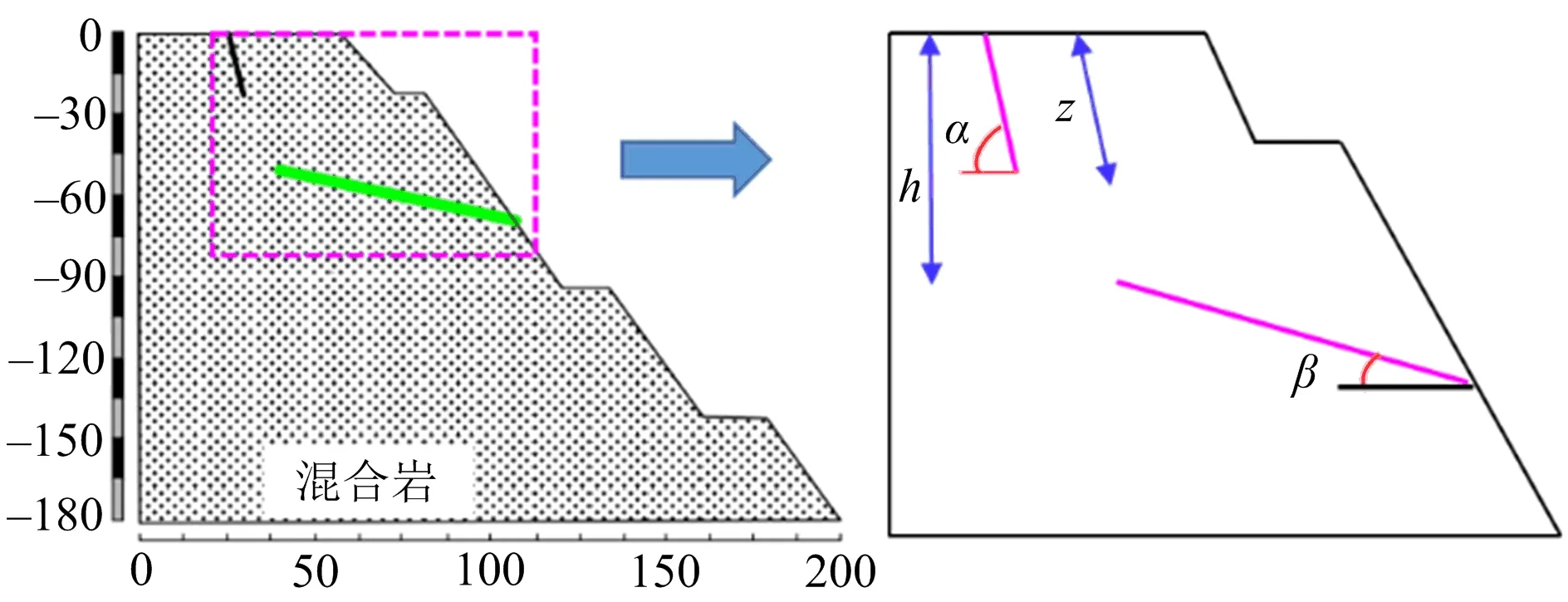
图10 工程地质剖面及裂隙概化模型Fig.10 Engineering geological section and fracture generalization model

将上述参数代入式(23)可得到边坡在爆破作用下和正常工况下的复合应力强度因子为1.48和1.19，进一步代入式(24)可得到边坡在爆破作用下和正常工况下稳定性系数为1.29和1.60，联立式(17)、(18)和(21)可得边坡在爆破作用下和正常工况下后缘裂隙起裂角为-52.7和-51.8。依据文献[6]中极限平衡法计算边坡在爆破作用下和正常工况下稳定性系数为1.42和1.83。

从上述计算结果可知，采用本文所推导方法和极限平衡法计算边坡安全系数的结果相差不大，这说明了本文所采用方法的合理性。本文所推导方法比极限平衡法计算结果偏小，这表明采用断裂力学法对边坡稳定性的判断更加安全可靠。

5 结论

1)基于断裂力学理论，推导了爆破作用下边坡后缘裂隙尖端复合应力强度因子表达式，重新定义了边坡稳定性系数计算方法。

2)爆破荷载的作用，改变了裂隙尖端应力场的分布情况，增加了裂隙尖端复合应力强度因子，降低了边坡稳定性系数。

3)后缘裂隙角度、平均高度、裂隙长度和爆炸应力波圆频率对裂隙起裂角和边坡稳定性系数有重要影响。后缘裂隙角度越大、裂隙越长、频率越大和平均高度越小，边坡越不稳定。

4)采用断裂力学法对边坡稳定性的预测更加安全可靠，且能准确计算出裂隙起裂角的大小和方向，裂隙长度对裂隙起裂角无影响。