爆破振动下隧道初支混凝土振速衰减规律

唐先习，张春洋，王要武，李旦合，高毅仁，李明泽

(1.兰州理工大学土木工程学院，兰州 730000；2. 中铁二十一局集团第二工程有限公司，兰州 730000)

现今国内山岭隧道的掘进开挖多采用钻爆法，该方法开挖隧道具有经济高效的优点；但开挖过程中附带的爆破振动效应会影响隧道的支护结构和围岩的稳定性，隧道初支混凝土喷层作为紧邻隧道钻爆掘进面的支护结构，受爆破振动的影响最大，国内外学者对爆破振动对隧道结构影响进行了不同的研究。饶增[1]通过试验研究分析了棋盘山隧道爆破振动衰减规律，在此基础上研究了爆破振动对喷射混凝土的作用机理，给出了网喷混凝土最大安全振速的建议值。郑明新等[2]运用现场测试技术与数值模拟研究了爆破振动对邻近高铁隧道衬砌结构的振动影响。卢文波等[3]利用波函数展开法，分析了爆破振动对邻近圆形硐室的影响，并得到爆破振动下圆形地下硐室围岩的应力和位移表达式，并分析了不同因素下硐室围岩安全振速。范凯亮[4]利用MIDAS/GTS NX有限元软件建立有限元模型，研究爆破施工对短龄期初支混凝土喷层的破坏范围，给出了不同龄期下初支混凝土喷层的安全振速建议值，指导隧道钻爆开挖和初期支护的施工。本文结合成昆铁路扩能工程沈家坝1号隧道的实际工程情况，采用理论分析、现场试验等方法围绕爆破振动对隧道初支混凝土喷层力学特性展开研究，实现钻爆施工现场爆破振动控制，具有重要的理论价值和实际工程意义。

1 爆破振动对短龄期初支混凝土影响机理

隧道初支混凝土由喷射混凝土构成，喷射混凝土强度形成过程和普通模筑混凝土相同，依靠水泥的水化作用形成水化硅酸钙，凝结骨料并填充骨料之间的空隙，从而形成一个密实结构体。喷射混凝土施工过程中采用喷射机械压缩空气或其它方式产生动力，将混凝土和速凝剂或其它外加剂同时从喷射枪中高速喷射出，挤压紧贴于需要加固的喷射面上，如建筑物、围岩、边坡等地方。喷射混凝土相较普通混凝土其最大的特点是早强特性，初凝时间一般在1～3 min左右，终凝时间一般在3～9 min，凝结硬化时间较普通混凝土很短，较短时间内有较高的强度增长，其波阻抗短时间内也有较高的增长，所以研究爆破振动对早龄期初支混凝土的影响必须考虑速凝剂的影响。除此之外，喷射混凝土材料中碎石粒径较小，具有较好的柔性，但初支混凝土仍为脆性材料，其抗拉强度只有抗压强度的1/18～1/8。爆破动载作用下在喷射混凝土内部产生拉应力对其受力状态是极为不利的。关于爆破振动对初支混凝土影响机理如下：

1)初支混凝土凝结硬化期间胶凝材料的凝聚强度不够高，爆破产生的应力波在喷射混凝土内部传播的过程中会在喷射混凝土内部产生切向拉应力，当拉应力过大的时候会造成胶凝材料和骨料之间的开裂，形成贯通性裂缝，造成结构的整体性变差、抗渗性降低，过量频繁的爆破也会造成初支混凝土结构内部产生初始缺陷，影响结构后期的强度增长。

2)初支混凝土经过空气挤压喷射附着在围岩壁面上，喷射混凝土和围岩壁之间的黏结力随混凝土的凝结硬化不断增强，但凝结硬化期间喷射混凝土和围岩壁之间的黏结力相对较弱，且凝结硬化期间喷射混凝土的波阻抗小于围岩波阻抗，此时喷射混凝土和围岩之间的黏结面是一层薄弱不耦合界面，当较强的爆破应力波在不耦合界面上传播时，会造成喷射混凝土和围岩黏结面的脱开和开裂。

3)初支混凝土通常和钢筋网片、钢拱架结合构成隧道初期支护的一部分，凝结硬化期间喷射混凝土和钢筋、钢拱架之间的黏结作用处于发展阶段，较大的爆破动载作用会造成喷射混凝土和钢筋、钢拱架之间的脱空。

2 沈家坝1号隧道爆破振动监测试验

2.1 工程概况

沈家坝1号隧道工程位于四川省凉山州冕宁县成昆铁路复线峨眉至米易段，隧道里程DK388+375～DK389+602，全长1 227 m，为单洞双线隧道，线路纵坡为8‰的单面下坡。隧道穿过花岗岩地层，最大埋深210 m。隧道围岩级别：Ⅴ级827 m，Ⅳ级180 m，Ⅲ级220 m。隧道所处位置属中山河谷地貌，地形起伏大，沟谷下切深，相对高差在60～200 m，位于安宁河谷右岸，为一侧傍山隧道。

2.2 爆破设计方案

上台阶断面面积为80 m2，炮孔按照位置不同作用不同可分为：一级掏槽、二级掏槽、辅助孔、内圈孔、周边孔、底板孔、大块解小。爆破设计参数：钻孔深度3 m，循环进尺3 m，炮孔利用率95%，单耗1.19 kg/m3。炮孔用专制炮泥填塞，填塞长度不小于60 cm。炸药使用2#岩石乳化炸药，药卷密度0.95～1.25 g/cm3，炸药密度1.00～1.25 g/cm3，爆速≥4.0×103m/s，猛度≥12 mm，殉爆距离≥3 mm，做功能力≥240 ml。爆破段位使用数码电子管控制，延迟精度可控制在1 ms。炮孔孔底填塞水袋，确保粉尘浓度降低90%。Ⅲ级围岩上台阶炮孔布置如图1所示。

图1 Ⅲ级围岩上台阶炮孔布置
Fig.1 Layout of upper bench blast holes in classⅢ surrounding rock

2.3 试验方法及测点布置

爆破振动试验仪器选择TC-4850爆破测振仪，采样频率1～50 kHz之间多档可调；频响范围0～10 kHz；记录方式为连续触发记录，可记录128～1 000次；记录时长在1～160 s可调。量程最大值为39 cm/s；记录精度为0.01 cm/s，本试验测振仪外接三轴向速度传感器监测初期支护振动响应。

根据掌子面开挖后的碎石坡脚现场结果显示，掌子面爆破后的碎石主要集中在距掌子面0～10 m范围。为防止传感仪器受到飞石影响，距掌子面10 m范围内不设测点。测点布置如图2所示，结合本隧道的工况情况，隧道属大断面隧道，隧道拱顶位置较高，测点布置在拱顶对于仪器的摆放收取极为不便。拱脚振速太小，其结果反映初期支护振动响应代表性不足，因此仪器摆放在拱腰下侧的位置，测点高出下台阶面1 m，拱顶6.5 m。安装时保证传感器的x方向垂直指向爆心，y向垂直指向初期支护，z向垂直朝上，并要保持传感器水平。

图2 爆破振动监测点布置Fig.2 Layout of blasting vibration monitoring points

3 爆破振动信号时-频分析

由爆破振动试验采集得到的信号(见图3)可知，爆破振动信号有11个波峰，波形较大的峰值出现在第一波峰和第二波峰(见图3d)，峰值最大位置出现在第二波峰。第一波峰对应3段一级掏槽爆破，第二波峰对应4段二级掏槽爆破。在炸药用量上，二级掏槽爆破用的炸药量最多，一级掏槽爆破炸药量第二。因此由二级掏槽爆破引起第二个波峰的峰值最大，一级掏槽爆破引起的第一个波峰次之。从不同炮孔面对的自由位移面讲，掏槽爆破仅有一个临空面，炸药做功释放能量时，爆破时岩石对炸药释放能量的过程有很大的夹制作用，这样造成炸药做功释放的能量有很大一部分会以地震波的形式传播，由此掏槽爆破引起振动响应最大，爆破振动最大的2个峰值出现在一二波峰位置，对应在3、4段位上的一二级掏槽。

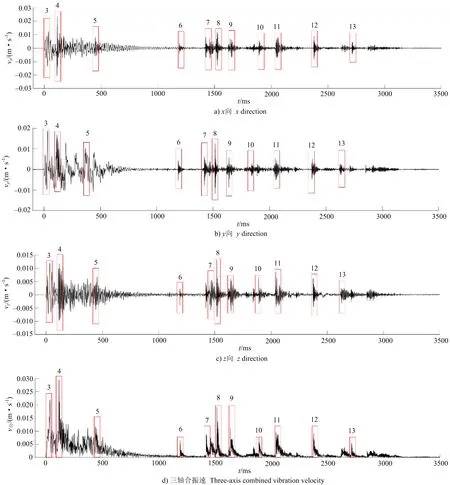
图3 爆破振动原始信号波形Fig.3 Original signal waveform of blasting vibration

全面分析爆破振动对隧道初支的影响，需要对爆破振动信号进行时-频特征分析。查阅爆破振动信号时-频分析资料，发现小波变换的方法在爆破振动信号的时-频分析中应用成熟广泛，而且方便易用。

使用小波变换对爆破振动信号的时-频分析的理论基础可简述为：对爆破振动信号进行分层重构，得到不同频带上爆破振动能量分布和振动强度的时间变化规律。分析过程中，很重要的一步就是振动信号的分解层数和小波基函数的选择，当采用二进小波时，函数f(t)的分层关系如下：

f(t)=A1(t)+D1(t)=A2(t)+D2(t)+D1(t)=…=An(t)+Dn(t)+…+D1(t)

(1)

式中：Ai(t)(i=1,2,…,n)为f(t)分解的低频部分；Di(t)(i=1,2,…,N)为f(t)函数高频部分；n为分解层数。

当f(t)爆破振动信号为x(t)时，有x(t)=f(t)，式(1)简化形式为

(2)

信号分解层数确定，试验仪器对爆破振动信号采样时采样频率为8 000 Hz，由采样定理可知该信号的最大频率4 000 Hz，结合式(1)和式(2)，爆破振动信号小波变换分解如图4所示，从而确定需要对爆破振动信号进行n=9层分解。

图4 爆破振动信号9层小波变换分解Fig.4 9-layer wavelet transform decomposition of blasting vibration signal

小波基函数选择根据原始振动信号和重构信号之间的相对误差判定：

(3)

式中：δ为相对误差；x0(t)为原始爆破振动信号；xr(t)为重构的爆破振动信号。

本试验使用小波变换对爆破振动信号进行时-频分析时选用db8小波基函数。分解过程采用MATLAB语言程序调用小波工具箱，使用db8小波基函数对图3中x轴向振速信号进行小波变换分解，9个频带上的结构如图5所示。

由爆破振动信号分解至各频带上的幅值情况(见图5)可知，振动能量主要集中的频带为31.25～62.5 Hz、62.5～125 Hz、125～250 Hz，爆破振动信号的能量分布在低频带范围，这和文献[5]给出爆破振动信号的能量主要集中在低频范围内结论一致；从时域上对爆破振动信号振动能量集中的主频带分析，可看出主频带能量振动信号幅值出现在0～300 ms，进一步证明爆破振动信号的能量主要由掏槽爆破产生。

4 振动试验数据回归分析

4.1 数据回归分析方法

爆破振动数据的回归必须依赖可靠的经验公式，使用经验公式法研究隧道初支爆破振动衰减规律方面，根据我国《爆破安全规程》(GB 6722-2014)[14]萨道夫斯基经验公式：

(4)

式中：v为质点振动速度, cm/s；Q为炸药量，分段爆破时为单段最大炸药量, kg，一次起爆为整体装药量, kg；R为测点到爆心的距离；k为公式系数；α为衰减指数。k、α取值和地质地形条件相关。关于不同岩性k、α建议取值，我国的《爆破安全规程》(GB 6722-2014)根据不同的岩性给出了建议范围(见表1)。

表1 不同岩性的k、α值

根据萨道夫斯基经验公式对试验数据进行回归分析，求解经验公式中的k、α值。Matlab软件中有多重线性函数，只需编辑程序语言对其调用即可。在对试验数据进行线性回归分析的时候，需要将萨道夫斯基经验公式转换程线性方程。将式(4)左右两端同时取对数得到式(5)。

(5)

(6)

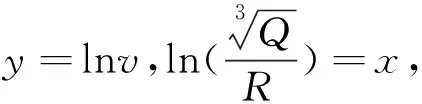
y=ax+b

(7)

式中：a=α，b=lnk。

式(7)可用一元线性回归进行求解：

(8)

(9)

式(8)和式(9)式的相关系数：

(10)

在MATLAB软件中多重线性回归函数公式可直接实现式(8)和式(9)对式(10)式线性方程进行求解，得到a、b值。MATLAB软件中的多重线性回归函数公式如下：

[b,Bint,r,Rint,Stats]=regress(y,X,alpha)

(11)

式中：b为回归系数估计值；Alpha为显著水平；Bint为回归系数估计值置信区间；R为各系数的残差；Rint为各系数的残差置信区间；Stats为向量值，其中向量值分别代表相关系数的平方、F值和显著性概率P。

使用MATLAB软进行多重线性回归函数求解时，首先要对爆破振动数据进行对数化预处理：

(12)

式中：v等于vx、vy、vz、v合。

按照式(12)对爆破振动数据进行对数化处理，得到爆破振速数据回归分析对数化预处理结果如表2所示。

表2 爆破振速数据回归分析对数化预处理结果

使用MATLAB调用多重线性回归函数，对表2的数据进行求解处理，得到方程y=ax+b的系数值a、b。由上文知萨道夫斯基经验公式的k、α与a、b之间的关系为α=a，lnk=b。由此各轴向振速的萨道夫斯基经验公式得以确定。根据回归解求得的萨道夫斯基经验公式，拟合沈家坝1号隧道初支混凝土喷层的爆破振动和炸药量爆心之间关系，从而得到初支混凝土喷层的爆破振动衰减规律。

4.2 初支混凝土喷层爆破振动衰减规律

根据爆破振动数据回归分析的方法，求解得到各轴向振速的萨道夫斯基经验公式：

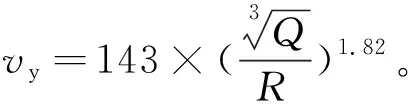
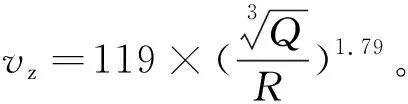
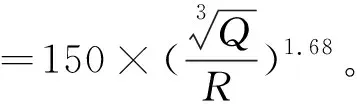
对得到的萨道夫斯基经验公式k、α参数(见表3)统计，与表1中不同岩性k、α值进行对比。求得的k在119～150之间，α在1.68～1.82之间。振动试验监测区段里程在DK389+020～DK389+240之间，围岩性质是Ⅲ级围岩，围岩性质较好，岩石性质介于中坚硬岩石之间。根据表3可知，中坚硬岩石k取值范围在50～250之间，中硬岩石α取值范围在1.3～1.8之间。现场爆破振动监测试验求得萨道夫斯基经验公式的k、α参数和《爆破安全规程》(GB 6722-2014)[14]给出不同岩性k、α建议值之间比较契合。

表3 萨道夫斯基经验公式k、α

为了能更好地分析初支混凝土喷层爆破振速衰减与炸药量、爆心距之间的关系。将炸药量R和爆心距Q进行捆绑，对萨道夫斯基经验公式进行改写。

Y=k(X-1)α

(13)

根据式(13)对求解得到各轴向振速的萨道夫斯基经验公式进行改写，结果如下：

x轴向振速的衰减曲线为Y=139(X-1)1.73。

y轴向振速的衰减曲线为Y=143(X-1)1.82。

z轴向振速的衰减曲线为Y=119(X-1)1.79。

三轴向合振速的衰减曲线为Y=150(X-1)1.68。

将各轴向的振速衰减曲线进行对比，结果如图6所示。

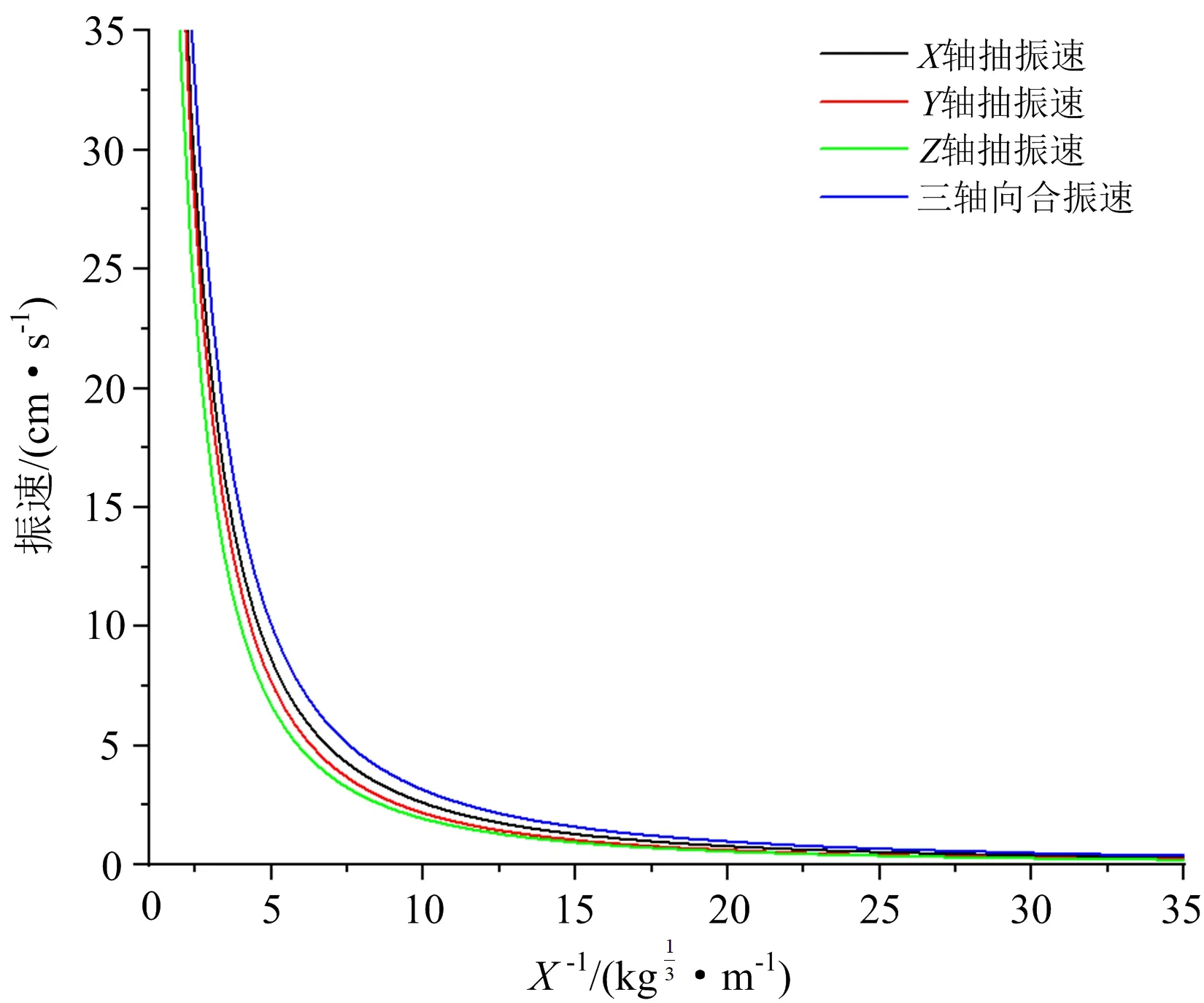
图6 各轴向振速衰减规律对比Fig.6 Comparison of attenuation laws of axial vibration velocity

由图7可知，相同的炸药量，初支混凝土喷层试验测点位置各轴向振速表现为：三轴向合峰值振速>x轴向峰值振速>y轴向峰值振速>z轴向峰值振速。传感器x向指向爆心，y向垂直指向初支混凝土喷层，z轴向垂直于地面，根据爆破地震波作用下隧道的变形分析可知，试验测点位置初支混凝土喷层主要受纵向拉压位移和横向拉压位移影响较大。根据以上分析还可知，三轴向合振速峰值最大，用三轴向合振速描述初支混凝土喷层振动响应情况更具有代表意义。

5 结语

通过对沈家坝1号隧道的爆破振动监测试验，得到初期支护振动响应。根据掌子面爆破参数与峰值振速的分析，爆破作用下初期支护振动响应最大峰值位置由掏槽爆破产生，分析原因一级掏槽爆破临空面最少，爆破承受较大岩石夹制压力，二级掏槽爆破炸药用量最多，从而带来隧道初支结构振动响应最大。使用小波变换法对爆破振动信号进行了时-频分析。根据萨道夫斯基经验公式对初期支护爆破振动数据进行回归分析得到了隧道初支的爆破振动衰减规律。