基于CDEM的岩石基坑爆破效果的数值模拟
2022-02-23任慧敏唐昊天张大帅赵红华
任慧敏,冯 春,唐昊天,张大帅,王 彪,赵红华
(1.工业装备与结构分析国家重点实验室,辽宁 大连 116024;2.大连理工大学工程力学系,辽宁 大连 116024;3.中国科学院力学研究所流固耦合系统力学重点实验室,北京 100190;4.中铁八局集团有限公司城市轨道交通分公司,成都 610000)
随着基坑开挖深度的不断增加,开挖面临的地质条件也更加恶劣,开挖到岩石层的基坑工程大多采用了延时爆破施工[1-4]。延时爆破又称为毫秒爆破,它在控制地震效应、扩大爆破规模、控制爆破块度和提高爆破效果方面,以及充分利用爆能、降低药耗等方面均起着重要作用。孔间毫秒延时间隔的长短是影响延时爆破效果的重要参数,国内外研究学者已经做过很多关于爆破效果相关的研究工作。杨仁树等[5]采用新型试验系统,用有机玻璃代替脆性岩石进行了延时爆破裂纹试验,验证了延时时间对爆生裂纹扩展有显著影响。Yan等[6]根据连续介质力学原理和动力非线性有限元理论,推导了炸药和岩石的控制方程,采用罚函数法结合腐蚀算法,建立了相应的有限元方程,并利用LS - DYNA分析了海底硬岩在延时爆破下的动力响应和爆破动力学特性,结果显示,合理采用排间延时爆破,可使矿石得到彻底破坏,从而提高岩石爆破质量。Choudhary等[7]利用粒径为3~7 mm的骨料或筛分钻屑和合理的行间延时时间,减少钻铤产生的巨砾,增加淤泥堆的松散度,从而提高爆破效率及其效果。Wang等[8]基于哈里斯爆破数学模型和叠加法,提出了一种装药结构多平面检测优化算法(MDO),并通过大直径深孔爆破作业验证MDO算法能改善岩石破碎,提高炸药能量利用率。Yuan[9]等建立1个带有2个圆形孔的矩形颗粒组合体模型,以相邻两孔间距和延时爆破延迟时间为主要变量,分别考虑系数为1.5的不耦合装药,发现孤立粒子或约束弱化粒子的碰撞作用对裂隙网络的形成起着至关重要的作用。潘博等[10]对不同节理角度的试件进行SHPB试验,并结合核磁共振成像系统得到最利于岩石破碎的荷载与节理的成角范围。
从以上研究成果可以看出,目前针对岩石基坑爆破效果方面数值模拟研究的成果仍然不多。因此,本文依托大连地铁 5 号线虎滩公园站基坑爆破工程,利用连续非连续方法CDEM中的块体动力学软件(GDEM-BlockDyna),研究岩石基坑模型在延时间隔时间和炮孔间距2个变量下的爆破效果及规律,并通过应力、振动速度、平均破碎尺寸、极限破碎尺寸、大块率及系统破裂度等指标进行综合分析。
1 连续-非连续数值模拟方法及力学模型
1.1 方法概述
GDEM 力学分析软件,以连续-非连续数值模拟方法(CDEM)为基础,通过 GPU/CPU的并行加速,可以分析材料在各类静、动荷载作用下的损伤破裂过程,实现工程尺度下材料的渐进破坏过程。CDEM是一种网格粒子高度融合的连续-非连续显式数值分析方法。该方法将连续介质数值方法与非连续介质数值方法进行深度融合,在能量层面实现了有限元、离散元及无网格算法的统一。该方法以Lagrange方程为理论基础,其表达式为
(1)
式中:ui,vi为广义坐标和广义速度;L为Lagrange函数,它是系统的能量;Qi为广义力。
由于是在积分意义下讨论连续-非连续计算过程,并没有考虑离散格式,所以无论是网格还是粒子(见图1),只要在其上引入积分点,就可以开展相应的工作。这就是连续-非连续方法囊括了有限元、块体离散元、颗粒离散元以及无网格等众多网格粒子这一类统一方法的原因。
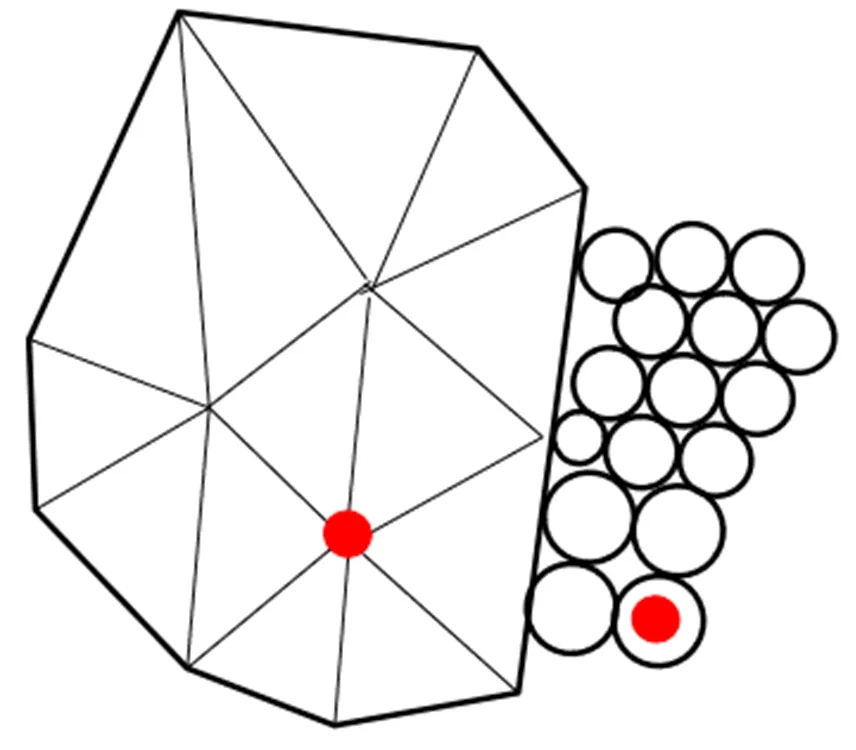
图1 网格及粒子积分点Fig.1 Grid and particle integral points
GDEM块体动力学软件(GDEM-BlockDyna)是一款基于多核CPU并行的显式动力学高效数值仿真软件,利用JavaScript的各类函数进行求解流程的精确控制。该软件以CDEM为计算核心,利用块体表征材料的连续介质特性,利用块体间的界面表征材料的非连续介质特性,块体边界及内部产生断裂,完成材料渐进破坏过程的仿真过程。该软件已经在岩土、采矿、爆破、隧道、油气、水利、地质等多个领域成功应用,服务于相关行业的科研及生产。
1.2 JWL点火爆炸模型
BlockDyna程序描述高能炸药爆轰产物压力-体积关系采用JWL状态方程[11]。高能炸药爆轰产物的单元压力p由状态方程(2)求得,具体可表述为
(2)
式中:V为相对体积;E0为初始内能密度,J/m3;A、B、R1、R2、ω为圆筒试验确定得出的常数[12-14]。
根据王鸿运[15]的研究成果,本次模拟中JWL状态方程各参数取值如表1所示。选择2号岩石乳化炸药[16]进行爆破模拟,计算所得炸药参数如表2所示。

表1 炸药JWL 状态方程参数

表2 炸药参数
爆炸模型的计算流程如图2所示。
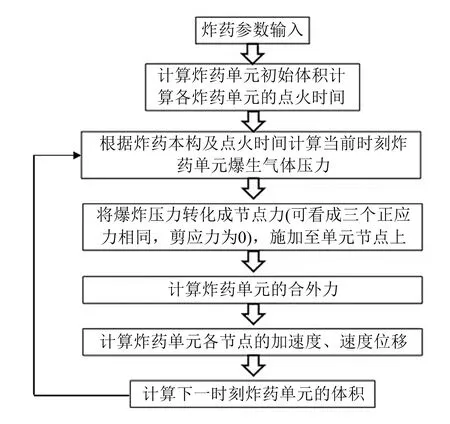
图2 爆炸模型计算流程Fig.2 Calculation procedure of explosion model
1.3 本构模型
采用岩体损伤破裂的力学模型,该模型由单元及虚拟接触面组成,即单元采用线弹性模型进行描述,输入包括密度及弹性模量等材料参数;单元间的虚拟接触面采用断裂能模型进行描述[17-18],输入参数包括黏聚力、内摩擦角、抗拉强度、法向连接刚度、切向连接刚度、拉伸断裂能、剪切断裂能。一般情况下,单元及虚拟接触面上的黏聚力、内摩擦角、抗拉强度的取值一致。
单元线弹性本构模型为
(3)
式中:σij为应力张量;Δσij为增量应力张量;Δεij为增量应变张量;Δθ为增量体应变;K为体积模量;G为剪切模量;δij为Kronecker记号;t1为下一时步;t0为当前时步。
接触面的损伤断裂计算首先要确定界面上下一时步的法向及切向试探接触力:
(4)
式中:Fn、Fs分别为法向、切向接触力;kn、ks为单位面积上法向、切向接触刚度,Pa/m;Ac为接触面的面积;Δdun、Δdus为法向、切向相对位移增量。
采用式(5)判断是否发生拉伸破坏、修正法向接触力及抗拉强度,为
(5)
式中:σt0、σt(t0)及σt(t1)为初始时刻、当前时刻及下一时刻接触面上的抗拉强度;Δun为本时刻接触面上的法向相对位移;Gft为拉伸断裂能,Pa/m。
采用式(6)判断是否发生剪切破坏、修正切向接触力及黏聚力,为
(6)
式中:φ为接触面的内摩擦角;c0、c(t0)及c(t1)为初始时刻、当前时刻及下一时刻接触面上的黏聚力;Δus为本时刻接触面上的切向相对位移;Gfs为剪切断裂能,Pa/m。
2 数值计算
2.1 工程概况
大连地铁5号线全长23.8 km,设车站18座,其中虎滩公园站为全线第二站。车站中心里程 YK2+646.963,车站起点里程 K2+577.963,车站终点里程K2+756.958,长178.995 m,宽约 20.0 m,高约18 m,设计底板高程-14.30 m,覆土厚 1.6 ~ 4.8 m,拟采用明挖法施工。
2.2 计算方案
在基坑开挖的过程中,最上层的素填土采用机械开挖方式,素填土的深度为3 m;对于强风化石英岩和中风化石英岩,采用爆破开挖方式,强风化石英岩和中风化石英岩的深度分别为1.5 m和22.5 m,本文着重分析中风化石英岩部分。由于爆破计算所划分的网格尺寸在厘米量级,若是建立三维数值模型,计算规模及耗时都是巨大的。故为了节约计算时间及成本,建立尺寸为20 m × 10 m的二维平切面模型(见图3)。该爆破模型内设置3个起爆点,炮孔直径设为250 mm,药包间距为L。模型的顶面设置为自由面,炮孔到自由面的距离为5 m,剩余的侧面以及底面设置为无反射边界条件(黏性边界),避免爆炸在外边界产生的应力波进行虚假反射,图3a中模型上半部红色边框范围内为爆破块度统计区域(域A)。在BlockDyna中导入ABAQUS软件划分的模型网格(见图3b),在起爆点周围进行网格的局部加密。
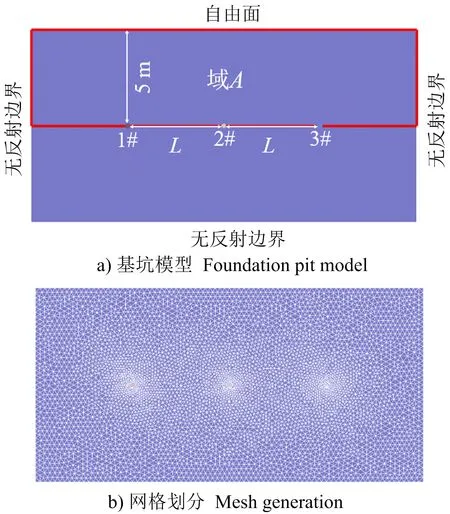
图3 爆破模型Fig.3 Blasting model
单纯考虑不同延时时间影响时,固定孔距L=5 m,目前国内部分延时爆破工程中多采用Δt=15~75 ms[19-20],经研究确定了合适的延时爆破时间,间隔时间依次是25、35、50、75 ms。
单纯考虑不同炮孔间距影响时[21-22],固定延时间隔时间为35 ms,炮孔间距依次取为3、4、5、6、7 m。
根据岩土的勘察报告,给出了中风化石英岩物理力学指标参数(见表3)。

表3 岩石参数
2.3 爆破效果评价指标
本文在考虑岩石基坑质点应力时程及峰值振速的同时,为了评定不同爆破参数对岩石的爆破效果,结合爆破后爆破块度统计区域的块度大小分布特点进行计算分析,采用4个评价指标[23]。利用脚本文件输出块体级配曲线信息,对数据进行整合后得到各指标具体数值[24-27]。
1) 平均破碎尺寸(d50):块体级配曲线信息中通过率为50%时相应的特征尺寸;该值与岩石的爆破碎块尺寸平均值成正比,该值越小表示模型破碎效果越好。
2) 极限破碎尺寸(d90):块体级配曲线信息中通过率为90%时相应的特征尺寸;该值与岩石爆破后的大碎块尺寸成正比,该值越小表示模型破碎效果越好。
3) 系统破裂度(Fr):数值模型虚拟界面产生破裂的面积占总面积的比值;该值越大表示模型破碎越完整。
4) 大块率(Br):块体级配曲线信息中特征尺寸大于0.9 m的岩石体积之和与模型总体积的比值,该值与模型破碎效果成反比。
3 计算结果分析
岩石基坑模型在基坑稳定线弹性分析的基础上施加爆炸冲击荷载,调用BlockDyna开展显式动力学模拟,设定每100时步向平台推送计算结果,可得到模型单元位置处位移、速度、加速度、应力等云图信息。在计算模型2、3炮孔连线中点与顶部自由面的交点处设置监测点,并开展数值计算分析。有关CDEM方法计算爆破的精度及合理性已经被大量文献验证[28-29],此处不再赘述计算的可靠性。
3.1 延时时间的影响
4种延时爆破模型监测点处的最大主应力时程曲线特性趋于一致,选取延时35 ms的应力时程曲线(见图4)进行表述,可以看出,选取的监测点处所受到的最大正应力正向峰值明显高于负向峰值,岩体以拉应力破坏为主导。最大主应力峰值分别为7.585 1、7.351 54、5.802 1、5.847 9 MPa,均大于爆破区域岩石的抗拉强度1.4 MPa,能达到岩石破坏的要求。延时时间对爆破前期作用的峰值差别不大,监测点的最大主应力峰值在第2个炮孔起爆附近,爆破后期曲线的跃增逐渐减小。间隔时间为25 ms和35 ms监测点处应力波波形产生重叠,岩石受叠加应力而易于破碎,爆破效果更好。
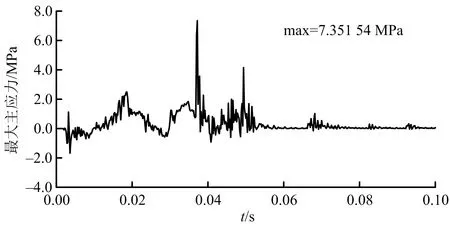
图4 延时35 ms的应力时程Fig.4 Stress time-history of 35 ms delay
4种延时爆破模型监测点处y方向(垂向)振动速度时程曲线如图5所示,在第二个炮孔起爆后振动速度急速增长,测点在y方向速度最大值分别为:17.32、16.67、18.89、17.03 m/s,此后速度基本保持不变。各模型速度最大值分别出现在41、53、67、106 ms,均延迟于第2炮孔起爆时间,说明测点位置处应力波持续冲击,使岩石块体加速产生位移。4种延时爆破模型监测点处振动速度最大值在16.67 ~18.89 m/s,相差最大约2.22 m/s,采用35 ms的延时间隔时间质点振速最小。
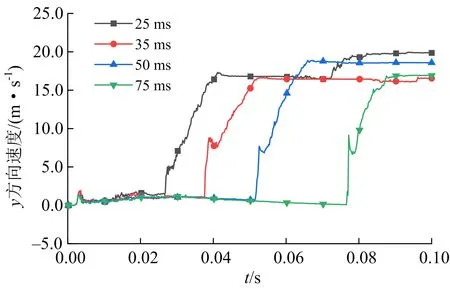
图5 y方向不同延时的振动速度Fig.5 Vibration velocity with different delay in y direction
分析监测点的应力曲线、振速曲线可知,延时35 ms时岩石爆破效果较好,因此选取延时35 ms分析岩石爆炸破碎的演化过程(见图6)。由图可知,第1个药包起爆后,冲击波自爆源向四周传播,炮孔附近的岩石被挤压粉碎,裂纹沿着网格呈放射性布满炮孔周围;随着时间的推移,冲击波衰减为压应力波,使岩石质点产生径向位移,在高压气体的膨胀、挤压作用下形成倒锥形裂纹;35 ms时第2个炮孔开始起爆,炮孔间应力波相互叠加,以致大块岩石被击碎成细小的粉粒;当时间大于86 ms后,破碎基本形成。
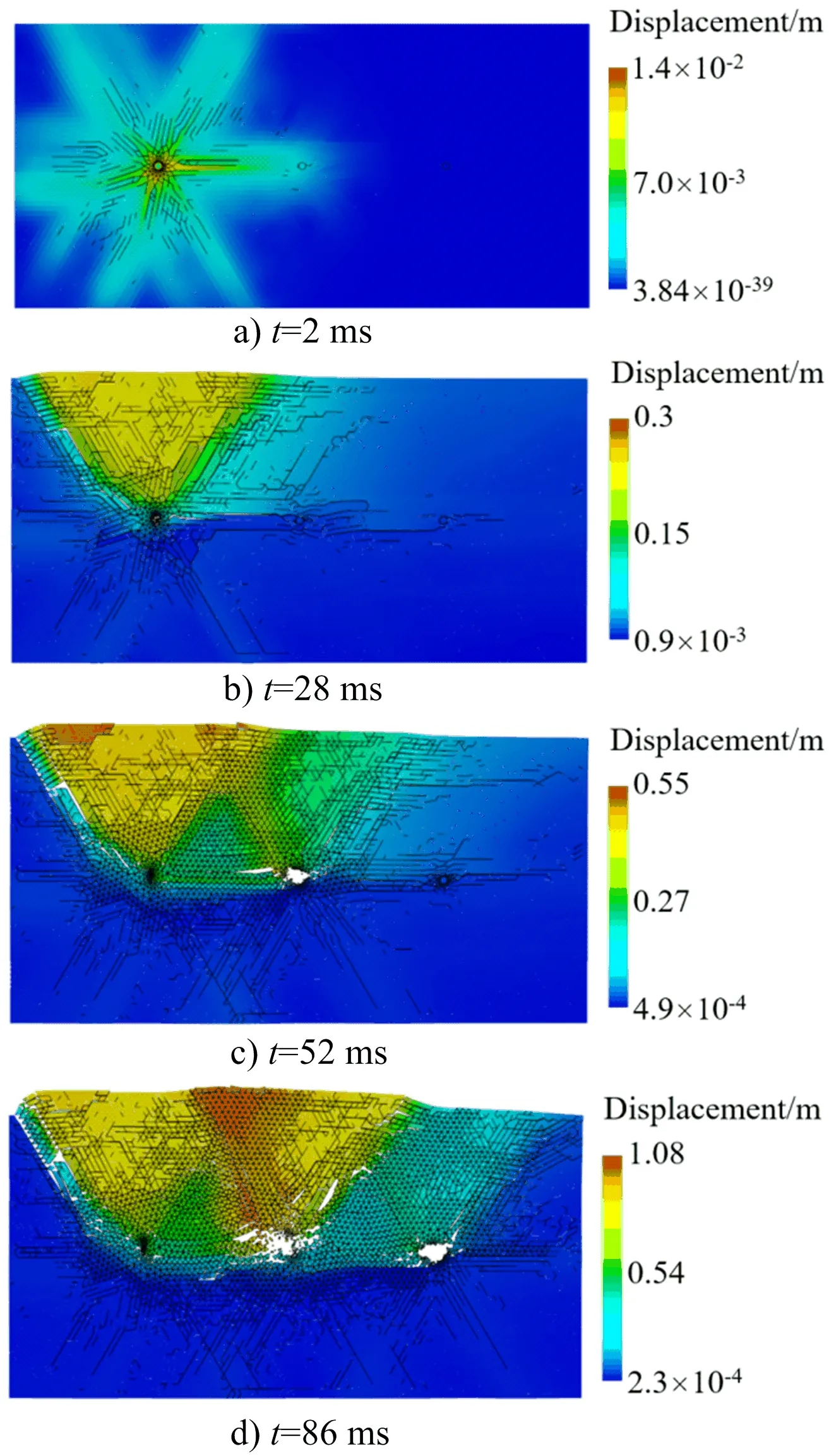
图6 延时35 ms时不同时刻的总位移云图Fig.6 Displacement contours at different time with 35 ms delay
延时35 ms爆破时,基坑模型的最终破碎形态如图7所示。由图7可知,逐孔起爆激活了几乎所有的预设虚拟界面,纵横交错的裂隙将岩石切割破碎,炮孔上侧的岩石破碎效果明显,下侧岩石局部产生拉伸裂隙,爆区顶部地表有大范围的隆起、位移。由模型爆破的最终形态可以看出,当延时间隔为35 ms时,岩石破碎块体较致密,爆破效果最好。延时25 ms爆破效果最差,较短的延时间隔不利于应力波在岩石裂隙内的传播和衰减,导致岩石局部产生过于破碎情况,而其他区域破碎不充分。

图7 延时35 ms的爆区破碎效果Fig.7 The fragmentation effect in blasting area of 35 ms delay
不同延时爆破的块体级配曲线如图8所示。随着特征尺寸的增大,块体的通过率逐渐增大;当延时间隔为35、50、75 ms时,通过率达到100%时的特征尺寸依次增大,岩石爆破效果逐渐变差,其中延时25 ms时的爆破效果最差(大块较多)。将监测数据进行处理得到平均破碎尺寸、极限破碎尺寸、系统破裂度、大块率等评价指标如表4所示。可以看出,延时为35 ms时,岩石破碎充分,碎块尺寸较小,爆破效果最好。
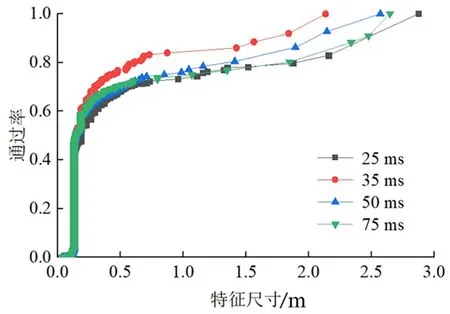
图8 不同延时间隔的块体级配Fig.8 Grading of blocks with different delay intervals
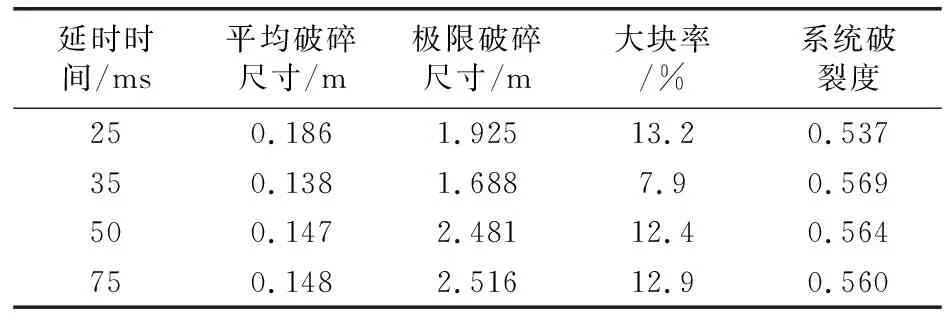
表4 不同延时的爆破破碎评价指标取值
不同延时爆破模型爆破块度统计区域的系统破裂度时程曲线如图9所示,分析可知:系统破裂度随着时间的增加而逐渐增大,曲线在每一个炮孔起爆后均有突变且破裂度增加速度加快;爆炸初期系统破裂度增加速度较快,当最后一个炮孔起爆后,破裂度的曲线斜率迅速变缓; 爆破完成后,25、35、50、75 ms延时爆破模型最终的系统破裂度分别为53.7%、56.9%、56.4%、56.0%,延时35 ms的系统破裂度较大,表征爆破效果更佳。
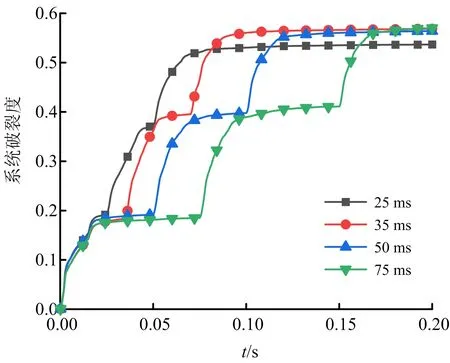
图9 不同延时下系统破裂度时程Fig.9 Time history of system fracture degree under different delay
3.2 炮孔间距的影响
炮孔间距L=5 m爆破后监测点处的最大主应力时程曲线如图10所示。不同炮孔间距下,监测点最大主应力分别为5.900 1、8.008 3、8.262 0、6.138 7、 11.957 3 MPa,均超过岩石抗拉强度。在第2个炮孔起爆后的一段时间内,测点处应力波动密集;L=5 m和L=6 m时,监测点处应力波重叠效果明显,受到的拉伸破坏作用加强,岩石裂纹发育充分。
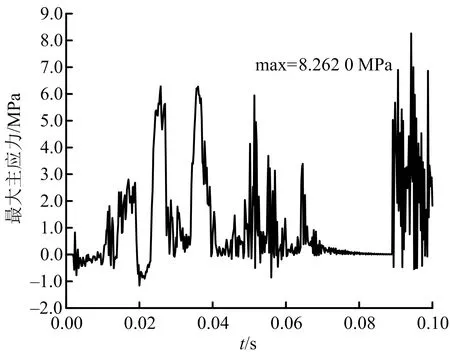
图10 炮孔间距5 m的应力时程Fig.10 Stress time-history of 5 m hole spacing
5种炮孔间距监测点处y方向振动速度时程曲线如图11所示,曲线整体走势一致呈上升状态,测点在y方向速度最大值分别为:20.16、19.02、17.82、14.61、11.97 m/s;随着L的增大,测点处y方向峰值振动速度逐渐减小,相较于L=3 m,相差最大约8.19 m/s。
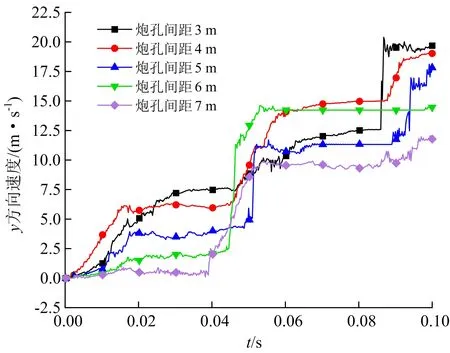
图11 y方向不同炮孔间距的振动速度Fig.11 Vibration velocity with different hole spacing in y direction
不同炮孔间距下的基坑模型的最终破碎形态相似,选取L=5 m进行表述(见图12)。由图可知,随着孔距的增加,爆区裂纹扩展更加充分,碎块尺寸更加均匀。当L=3 m时,由于炮孔间距过小,阻碍了应力波的传播,导致岩石局部产生过于破碎情况,而其他区域破碎不充分。当L=7 m时,由于炮孔间距过大,爆炸应力破坏效应减弱,导致炮孔周围出现较密集区域,其他区域碎块尺寸较大。由模型爆破的最终形态可以得出,当L=5 m和6 m时,岩石破碎块体较致密,爆破效果最好。
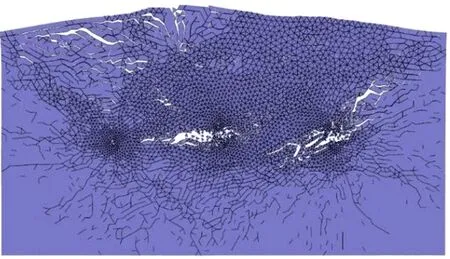
图12 炮孔间距5 m的爆区破碎效果Fig.12 The fragmentation effect in blasting area of 5 m hole spacing
不同炮孔间距的块体级配曲线如图13所示。可以看出块体的通过率随着特征尺寸的增大逐渐增大;随着炮孔间距的增大,通过率达到100%时的特征尺寸越小,岩石碎块越均匀;其中L=6 m时的特征尺寸略小于L=7 m的特征尺寸。将监测数据进行处理得到平均破碎尺寸、极限破碎尺寸、系统破裂度、大块率等评价指标如表5所示。从表5可看出,当L=6 m时,岩石破碎充分,碎块尺寸较小且均匀,爆破效果最好。
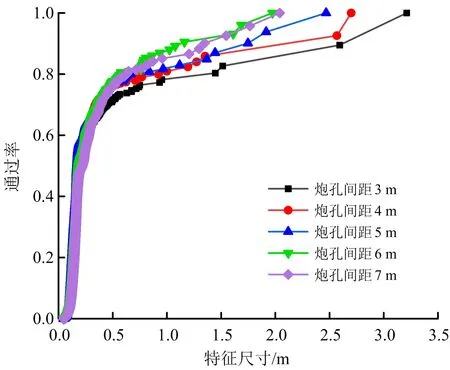
图13 不同炮孔间距的块体级配Fig.13 Grading of blocks with different hole spacing
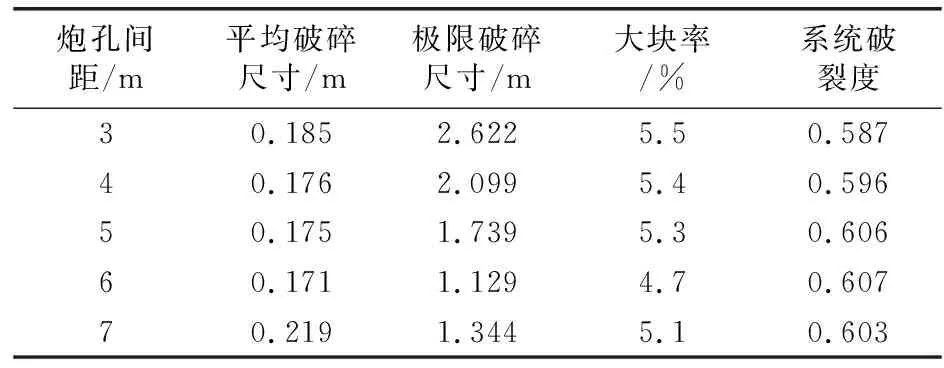
表5 不同孔距的爆破破碎评价指标取值
不同炮孔间距下系统破裂度时程曲线如图14所示,分析可知:系统破裂度随着时间的增加而逐渐增大,不同孔距的突变点大致相同;爆破完成后,5种炮孔间距爆破模型最终的系统破裂度分别为58.7%、59.6%、60.6%、60.7%、60.3%,L=6 m和L=7 m的系统破裂度较大,表征爆破效果更佳。
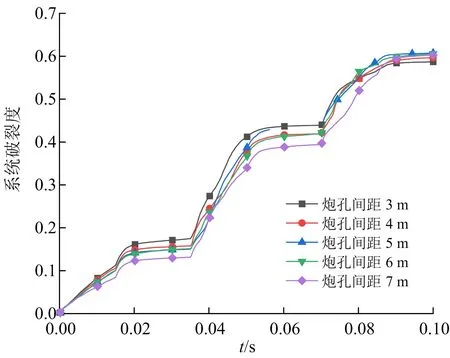
图14 不同孔距下系统破裂度时程Fig.14 Time history of system fracture degree under different hole spacing
4 结论
1)对不同延时爆破的计算模型进行爆破应力及振动速度分析,根据模拟结果,测点振动速度最大值在16.67~18.89 m/s,延时25 ms和35 ms均可获得较好的破碎效果,而延时35 ms引起的峰值振速较小。根据地铁基坑工程的爆破要求,延时35 ms的模型爆破效果更好。
2)延时35、50、75 ms时,平均破碎尺寸、极限破碎尺寸、大块率随着延时间隔的增大逐渐增大,系统破裂度随着延时的增大逐渐减小。从各指标可以看出,岩石爆破模型的损伤破裂效果随着孔间延时的增大而逐渐变差,延时25 ms爆破效果最差,较短的延时不利于应力波在岩石裂隙内的传播和衰减,导致岩石局部产生过于破碎情况,而其他区域破碎不充分。
3)炮孔间距L=5 m和L=6 m时,所选取的监测点所受应力波叠加破坏作用明显;测点振动速度最大值在11.97~20.16 m/s,测点处y方向振动速度峰值随着炮孔间距L的增大逐渐减小,故炮孔间距L=6 m的爆破效果优于L=5 m的爆破效果。
4)炮孔间距L=3、4、5、6 m时,平均破碎尺寸、极限破碎尺寸、大块率随着炮孔间距的增大逐渐减小,系统破裂度随着炮孔间距的增大逐渐增大。可以得出,随着炮孔间距的增大,破碎块体的均匀性逐渐提高,但炮孔间距L增加到7 m时,岩石的平均破碎尺寸达到最大,炮孔间距过大使得应力叠加效应减弱。
5)改变炮孔间距相对于改变延时时间大块率从7.9%到4.7%降低了3.2%,系统破裂度从56.9%到60.7%提高了3.8%,改变炮孔间距的爆破效果优于改变延时时间的爆破效果。
