不耦合系数对水下爆破破岩效果影响的数值分析

陈 涛，汪海波，王丽敏，吕 闹，宗 琦

(安徽理工大学土木建筑学院，安徽 淮南 232001)

水下爆破岩石，炮孔中会有水的存在，但经过爆破后会发现，炮孔中有水的存在，爆破会取得更好的爆破效果，即炮孔中有水的存在，爆破会更节省炸药。对于水下爆破工程，实际操作受到许多限制，因而对实际水下爆破工程中采用的孔网参数进行数值模拟十分有必要[1]。

李书萱等[2]分析了3种不耦合系数的试件内部裂纹数量及分布、粉碎区大小等情况，证明了存在一个最优的不耦合系数使爆破产生的能量达到最大。金鹏等[3]应用数值模拟的方法，证明了水不耦合装药结构增强了使岩体破碎和产生裂纹的效果。当岩体处于不同的地应力时，均对应着使爆破效果达到最佳不耦合系数。张迅[4]对固、液、气3种不同耦合介质的装药结构进行了数值模拟，确定了最优不耦合系数的范围。赵建平等[5]对不同工况进行数值模拟，证明了当地应力为0时，随着孔距的增大，炮孔连线的应力扩展范围逐渐增加，垂直炮孔连线的方向应力扩展范围逐渐减小；损伤面积与钟形曲线类似，因而存在最优的炮孔间距使得裂纹数量及破碎的范围达到最大。李洪伟等[6]对不同孔距的裂纹扩展及损伤半径进行了分析，当孔距不断增大时，炮孔周围的损伤更为充分，破碎面积增大，主裂纹增多，当产生的应力波发生叠加时，此时使裂纹扩展的更为充分。

基于此，以某微风化英安岩水下爆破工程为例，采用数值模拟的方法，对水下爆破工程用不耦合系数的有效应力分布进行数值模拟，得到不同不耦合系数时单孔爆破典型位置处有效应力峰值与水平距离的关系，确定炮孔间距的取值范围及最优不耦合系数，并分别对不同炮孔间距建模分析，从而获得符合可以使微风化英安岩破碎的孔网参数，为实际工程提供理论依据。

1 数值模拟

1.1 模型的建立

模型采用多物质ALE流固耦合算法，水、空气和炸药采用ALE算法，岩石采用LAGRANGE算法，空气的直径是炮孔直径的10倍。炸药、空气和水视为流体，为了实现能量的传递，炸药与空气间采用共节点来实现，岩石视为固体，流体与固体间采用流固耦合*CONSTRAINED_LA-GRANGE_IN_SOLID，从而实现爆炸能量在流体与固体之间的传播[7-8]。计算模型要能真实反映出爆炸时的应力分布，为实际操作提供理论支持，更直观的体现应力的传播，因而假定计算模型中的材料是各向同性、均质和连续的材料。为了方便研究间，模型采用厚度为1 cm薄片型，装药炮孔同时起爆。数值模型采用映射网格划分，选用SOLID_164实体单元，计算采用通用单位制cm-g-μs。考虑到爆炸应力波扩展过程需要时间，计算时间设为1 000 μs，每0.90 μs输出一步结果文件[9]。

在水下爆破工程实践中通常采用柱状装药，炮孔的直径大于药包的直径，即炸药与岩体之间有水的存在，为水不耦合装药。首先将计算模型简化为平面有限元问题，如图1所示，应用有限元软件，建立二维单孔爆破计算模型，统一单孔爆破模型尺寸为400 cm×400 cm，得到有效应力在岩石中的传播特性，拟合出关于距药柱不同的水平距离与峰值应力的关系曲线。在模型的四周设无反射边界条件，可以吸收剪切波和膨胀波来减小应力扩展到边界后反射所带来的干扰，使模型更加贴近于在无限岩体中的受力状态[10]。

图1 单孔水不耦合装药爆破计算模型Fig.1 Calculation model of single hole water decoupled charge blasting

1.2 材料参数

岩体采用MAT_PLASTIC_KINEMATIC，可以应用于应变率效应各向同性随动塑性强化的材料，微风化英安岩的动态抗压强度测试结果表明岩石平均动态抗压强度达到75 MPa以上时，认为岩石的破碎状态良好。即数值模拟时炮孔连心线上的测点Von-Mises应力达到75MPa以上，可认为岩石破坏[11]。模量采用的微风化英安岩具体物理力学参数如表1所示。

表1 岩石的材料参数

空气选用的是*MAT_NULL空材料模型，同时为了更加接近实际，使用LINEAR_POLYNOMIAL线性多项式来描述空气的状态方程：

p0=C0+C1ξ+C2ξ2+C3ξ3+(C4+C5ξ+C6ξ2)E1

(1)

(2)

式中：C0、C1、C2、C3、C4、C5和、C6为状态方程的参数；E1为单位体积内能；V0为初始相对体积。

空气状态方程参数如表2所示[12-13]。

表2 空气的状态方程参数

炸药选用*MAT_HIGH_EXPLOSIVE_BURN材料模型，并且配合JWL状态方程准确描述爆炸所产生的能量特性，式(3)为JWL方程爆轰压力的表达式：

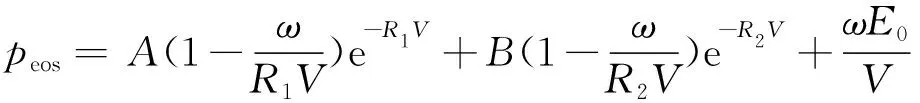
(3)

式中：peos为爆轰压力；A、B为炸药的材料常数，Pa；R1、R2、ω为炸药的材料常数，无量纲；E0为爆轰产物的初始内能；V为爆轰产物相对体积，无量纲。

炸药材料及JWL状态方程参数如表3所示[13-14]。

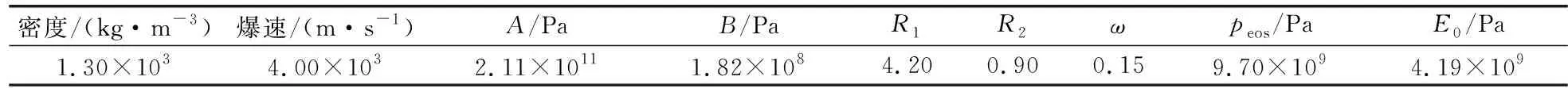
表3 炸药的状态方程参数

水选用的是LS-DYNA中的NULL空白材料模型，且满足GRUNEISEN状态方程为

(γ0+aμ)E0

(4)

式中：p为压力；E0为初始内能；c为剪切—压缩波速曲线的截距；S1、S2、S3为剪切—压缩波速曲线的斜率因数；γ0为GRUNEISEN常数；α为初始体积修正因数；ρ0为材料初始密度；μ为动力黏性系数，μ=ρ/ρ0-1。

水的具体参数如表4所示[15]。

表4 水的材料参数

1.3 计算工况设计

由于炮孔直径受钻孔设备的限制，因而会存在一些固定尺寸，典型的水下爆破工程地质条件、钻孔参数和装药参数如表5所示，可见不耦合系数大多在1.2～1.5。而数值模拟的诸多结果表明水不耦合装药其最佳不耦合系数取值范围为1.5～1.75，与实际水下爆破工程存在明显差别。选取具有代表性的实际水下爆破工程中常用的不耦合系数(K=1.21、1.28、1.35、1.44)，即炮孔直径115 mm，药包直径分别为95、90、85、80 mm进行数值模拟。

表5 典型水下爆破工程

2 模拟结果与讨论

首先对选取实际水下爆破工程中具有代表性的4组不耦合系数(K=1.21、1.28、1.35、1.44)，分别建立单孔模型进行计算，优选出最优的不耦合系数。采用最优的不耦合系数建立双孔的爆破计算模型，研究不同孔距对爆破破岩效果的影响。

2.1 单孔模型应力分析

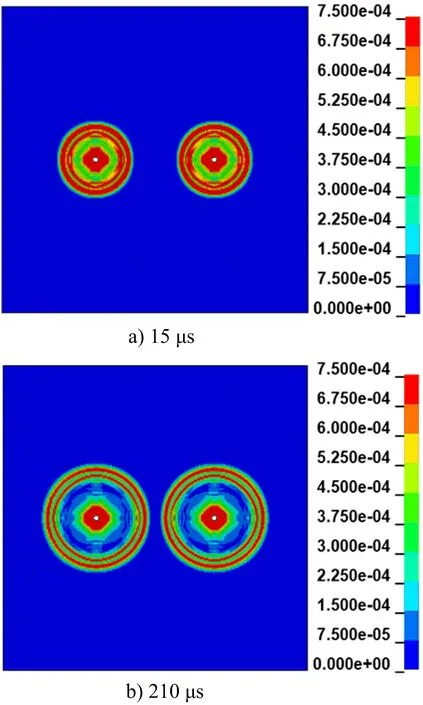
得到不同时刻单孔水不耦合装药爆破的应力云图如图2所示，在150 μs时，炮孔附近有效应力峰值在100 MPa以上，单元的峰值应力在距药柱水平距离125 cm以内衰减的较快，此后有效应力衰减的较为缓慢。

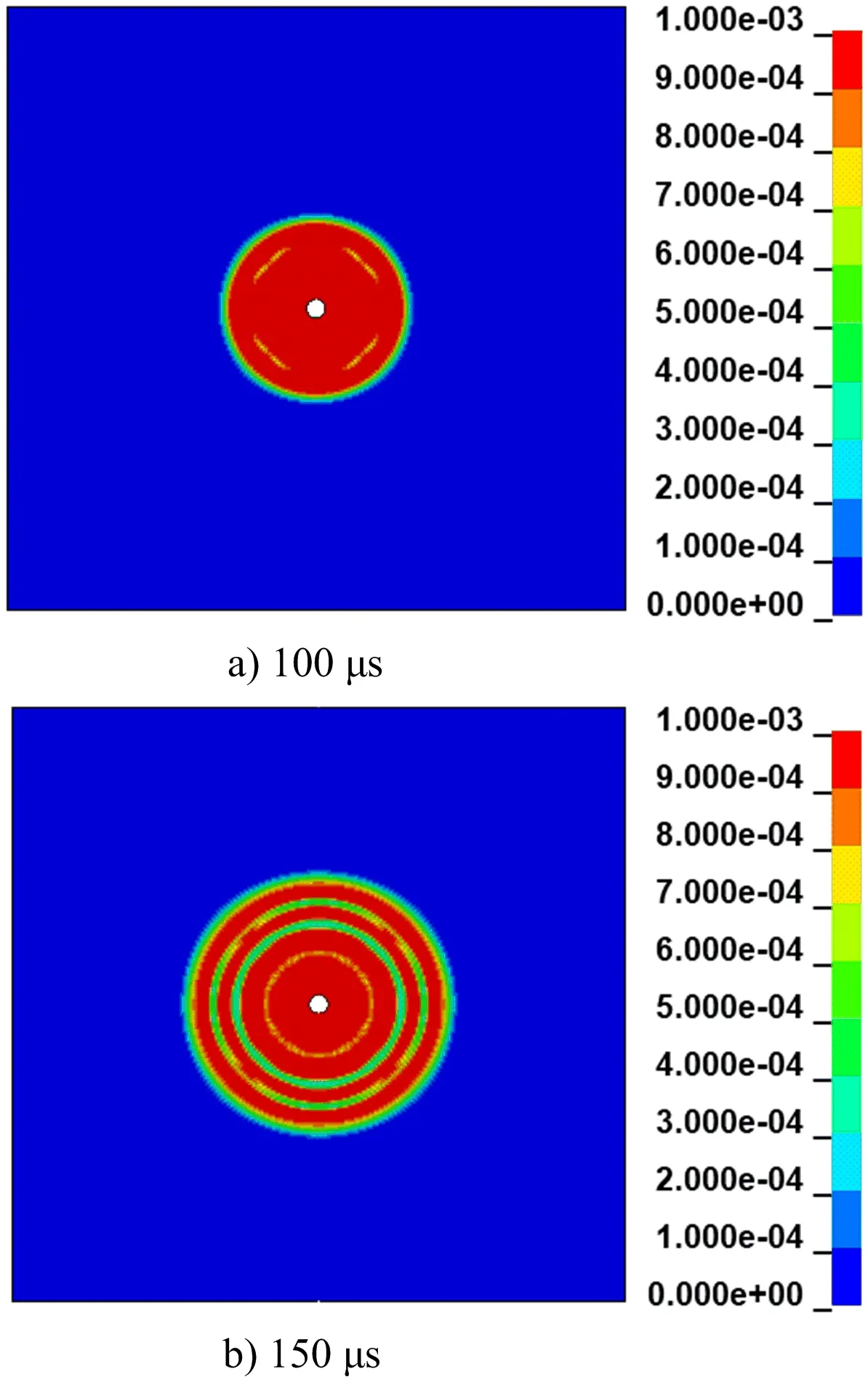
在计算模型炮孔一定距离处布置测点，如图3所示；不同不耦合系数下测点的峰值应力拟合出的曲线如图4所示，不同耦合系数炮孔孔壁的有效应力如图5所示。在岩石和水介质的交界处孔壁所受到的峰值应力最大，测点的峰值应力随着距药柱的水平距离的增大，峰值应力呈指数函数的形式衰减。结论表明在水下爆破常用的不耦合系数中，当不耦合系数K=1.21时，炮孔周围和孔壁的峰值应力始终最大，且随着不耦合系数的增大，炮孔附近的峰值应力有所减小。从而得出结论当不耦合系数在1.21～1.44时，随着不耦合系数的增大，炮孔周围的峰值应力和孔壁所受到的峰值应力呈现减小的趋势，因而双孔爆破模型使用不耦合系数K=1.21。通过单孔水不耦合装药的应力分布云图，取单元的有效应力的峰值，当峰值应力大于岩石的平均动态抗压强度认为岩石破碎状态较为良好。对不耦合系数K=1.21的单孔水不耦合装药爆破模型里面单元的峰值应力进行分析，测点的峰值应力在叠加后均达到75 MPa以上左右认为岩石破碎状态良好，块度较小。

图3 单孔测点的布置Fig.3 Layout of singlehole measuring points

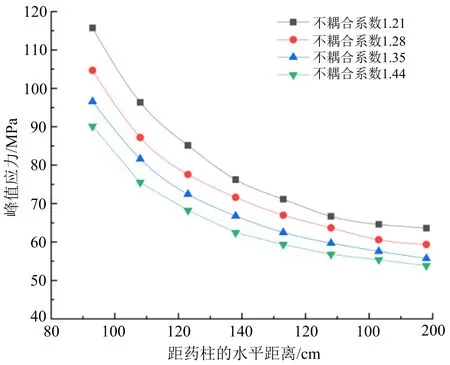
图4 峰值应力-距药柱距离关系Fig.4 Relationship between peak stress and distance from charge column with different uncoupling coefficionts

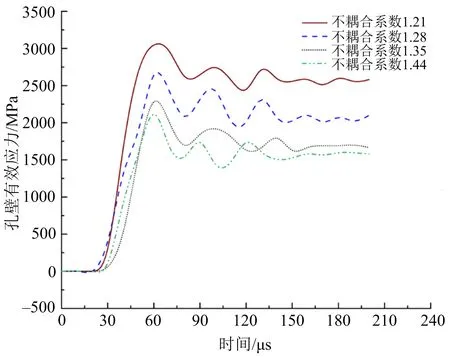
图5 不同不耦合系数孔壁应力-时间关系Fig.5 Relationship between hole wall stress and time with different uncoupling coefficients

2.2 双孔模型应力分析

双孔爆破计算模型需要考虑到两炮孔间有效应力的叠加，因而距药柱的水平距离为120～180 cm为初步确定满足微风化英安岩破碎的范围。根据应力叠加原则确定炮孔间距在240～360 cm时满足水不耦合的装药结构下使微风化的英安岩破碎。因而分别对炮孔间距为240、280、320、360 cm分别进行建模，取两炮孔单元的峰值应力，从而确定最优的炮孔间距。统一双孔爆破计算模型，尺寸为720 cm×720 cm，不耦合系数K=1.21，得到不同炮孔间距不同时刻应力云图。由应力云图可以发现，装药起爆后的一段时间内炮孔周围的岩体之间的受力是互不干扰的。不同炮孔间距，孔心线出现应力叠加的时间也不同，每当间距扩大40 cm，炮孔间出现应力叠加的时间延迟40 μs。随着炮孔间距的增大，孔心线中点处峰值应力也随之变小，对比不同炮孔距的应力云图，发现双孔爆破会在炮孔连线中点处形成能量积聚和应力叠加，使双孔间的区域更易破碎。随着孔间距的增大，沿孔心线方向应力逐步扩展变大，垂直于孔心线方向应力逐渐变小，存在一个最佳孔间距使岩石破碎范围最大，当孔间距为280 cm时如图6所示，炮孔间的有效应力峰值均在75 MPa以上，垂直孔线方向影响范围也为最大。

为了探究模型在相同装药的装药结构下，岩石在不同炮孔间距，炮孔连线上的有效应力的传播规律和峰值应力大小，取5个测点如图7所示，对比不同炮孔间距上测点的峰值应力大小。根据图8和图9可以获得测点的峰值应力最小点为距两炮孔中心10～30 cm左右的范围。由图8可知，孔距为240 cm，在400 μs时两炮孔中心的峰值应力最大达到106.49 MPa，测点的最小峰值应力为87.61 MPa；孔距为280 cm，在440 μs时炮孔中心的峰值应力最大达到95.96 MPa，测点的最小峰值应力为76.18 MPa；孔距为320 cm，在470 μs时炮孔中心的峰值应力最大达到86.48 MPa，测点的最小峰值应力为67.95 MPa；孔距为360 cm，在500 μs时炮孔中心的峰值应力最大达到75.12 MPa，测点的最小峰值应力为58.75 MPa。因而，可以得出结论当炮孔间距为280 cm时，炮孔连心线上的所有单元大于75 MPa，故为最优的炮孔间距。

图7 炮孔间距280 cm的测点布置Fig.7 Layout of measuring points with hole spacing of 280 cm

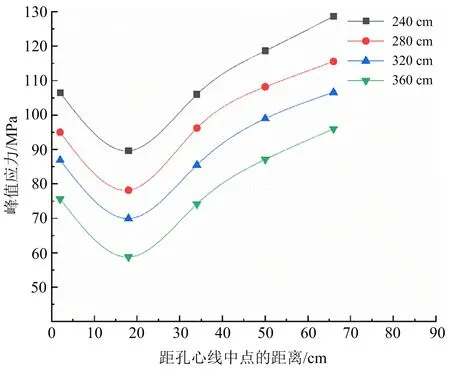
图9 不同炮孔间距测点的峰值应力Fig.9 Peak stress of measuring points with different hole spacing

根据双孔爆破模型的数值模拟计算结果显示当不耦合系数为K=1.21时，爆破时炮孔间的有效应力最大，确定炮孔的布置为梅花形，即炮孔直径115 mm、药包直径95 mm，孔距280 cm，排距240 cm。数值模拟结果显示炮孔间单元的峰值应力均可达到75 MPa以上，大于微风化英安岩的平均动态抗压强度，因而可以使岩体破碎。通过了解水下爆破工程中常用的炮孔直径，结合本文的数值计算结果，当岩石性质与微风化英安岩相似时，通过数值模拟给出以下推荐使用的孔网参数如表6所示，供实际的水下爆破工程参考。

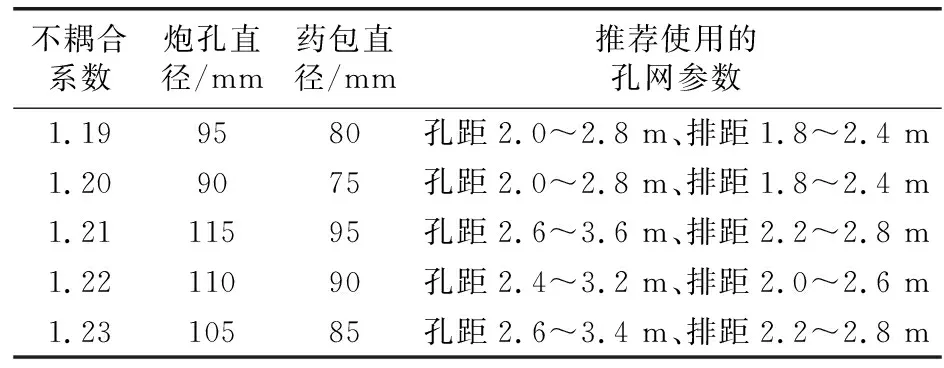
表6 水下爆破推荐使用的孔网参数

3 结语

1)对比水不耦合装药的四组不耦合系数(K=1.21、1.28、1.35、1.44)的数值模型，结果表明在不耦合系数K=1.21时孔壁和炮孔周围所受到的峰值应力最大，能量的传递效率最高，在不耦合系数为1.21～1.44范围内，随着不耦合系数的增大，孔壁与炮孔周围的有效应力峰值不断减小。

2)水下岩石为微风化英安岩，分析了不耦合系数K=1.21时水不耦合装药的四组不同孔距的爆破模拟结果，当考虑单元峰值应力，在炮孔间距为280 cm时，孔心线上的测点的应力峰值均达到了75 MPa以上，故岩石破碎状态良好，且块度较小，为最优的炮孔间距，炮孔的布置为梅花形故排距为240 cm。

3)在工况相同的情况下，改变爆破的孔网参数会改变了爆炸应力波的叠加效果。不耦合系数K=1.21时，分析不同炮孔间距爆破效果，应力云图显示随着孔间距增加，孔心线间的有效应力峰值随之减小，每当两炮孔间距增大40 cm，测点的峰值应力减小10 MPa左右，且双孔爆破所产生的应力并非单纯的单孔爆破模型所产生的应力叠加而产生的，而是由冲击波和爆生气体所产生的复杂的应力场。

4)水不耦合装药相对于空气不耦合装药增加了爆轰产物作用于岩体的时间和峰值，同时增加了能量传递的效率。水不耦合装药在爆炸时由于水相对于空气的压缩性相对较小，当其作为传递爆轰能量的耦合介质时，可有效提高爆炸能量的利用率，使得岩体受力更加均匀，使得岩石的有效破碎面积增大。