基于EMD分解的爆破振动信号主成分提取与分析

张声辉，高文学，刘江超，李小帅，胡 宇，张小军

(北京工业大学城市建设学部，北京 100124)

由于爆炸能量的瞬间释放，产生的爆炸应力波迅速沿着介质传播，致使很大范围内的周边建(构)筑物都会受到爆破振动的影响，所以其带来的隐患一直以来皆受到学者们的重点关注[1-2]。爆破振动监测可作为施工方案和参数设计优化的衡量手段，对工程的经济安全生产有着重要的指导意义和反馈价值[3]。

爆破振动信号受到复杂环境条件和监测仪器自身的限制，具有瞬时非平稳性的特点，基本都会包含噪声和基线偏移等杂乱的干扰信号成分，而它们为信号的关键分析带来较多困难[4-7]。现如今，各领域信号的处理方法和分析研究也渐为深入。由刚开始的傅立叶变换(FFT)，随继出现短时傅里叶变换(STFT)、小波变换(WT)、小波包变换(WPT)、希尔伯特-黄变换(HHT)等技术，这些方法皆被应用到爆破振动信号领域[8-15]。邱贤阳等[9]针对金铜矿边坡爆破获取了单段振速信号，利用EMD分解和Hilbert能量谱得到并探讨了不同延时下两段叠加信号的振动特性，分析了短延时爆破在不同条件下的信号叠加降振；曹晓立等[10]基于Hilbert-Huang 变换分析很好地反映了鲁坨路路堑边坡爆破信号的时频特征及能量分布情况；张其虎等[11]利用HHT法与EMD分解研究了不同药量对金沙矿业官房矿段地下浅孔爆破振动多参量的影响；钱守一等[12]和龚敏等[13-14]也将HHT瞬时能量对延时爆破的振动信号进行了精确识别与分析。上述学者也通过研究证明EMD分解相较于小波(包)分析有无需选定基函数的优点，因此，近年来通过HHT分析爆破振动信号较为广泛。

本文结合希尔伯特-黄(HHT)分析方法自适应性好的优点，基于崇礼国家跳台滑雪中心边坡岩体爆破现场振动监测采集的信号，通过EMD分解算法去除高频噪声和低频趋势项来实现爆破振动信号主成分的重点提取，并对爆破振动信号主成分展开了分析研究。

1 爆破振动监测试验

1.1 工程概况

崇礼国家跳台滑雪中心是2022年冬奥会主要比赛建设场地，距离城区20 km左右。施工建设区域的主要岩性为不同分化程度的花岗岩，根据局部山体开挖设计要求，崇礼跳台滑雪中心北侧边坡由上而下逐级采用台阶爆破开挖。台阶高度为10 m，边坡坡率为1∶0.9和1∶0.5，高程1 692 m的台阶宽度为4 m，其余均为2 m；爆破开挖的边坡设计如图1所示。

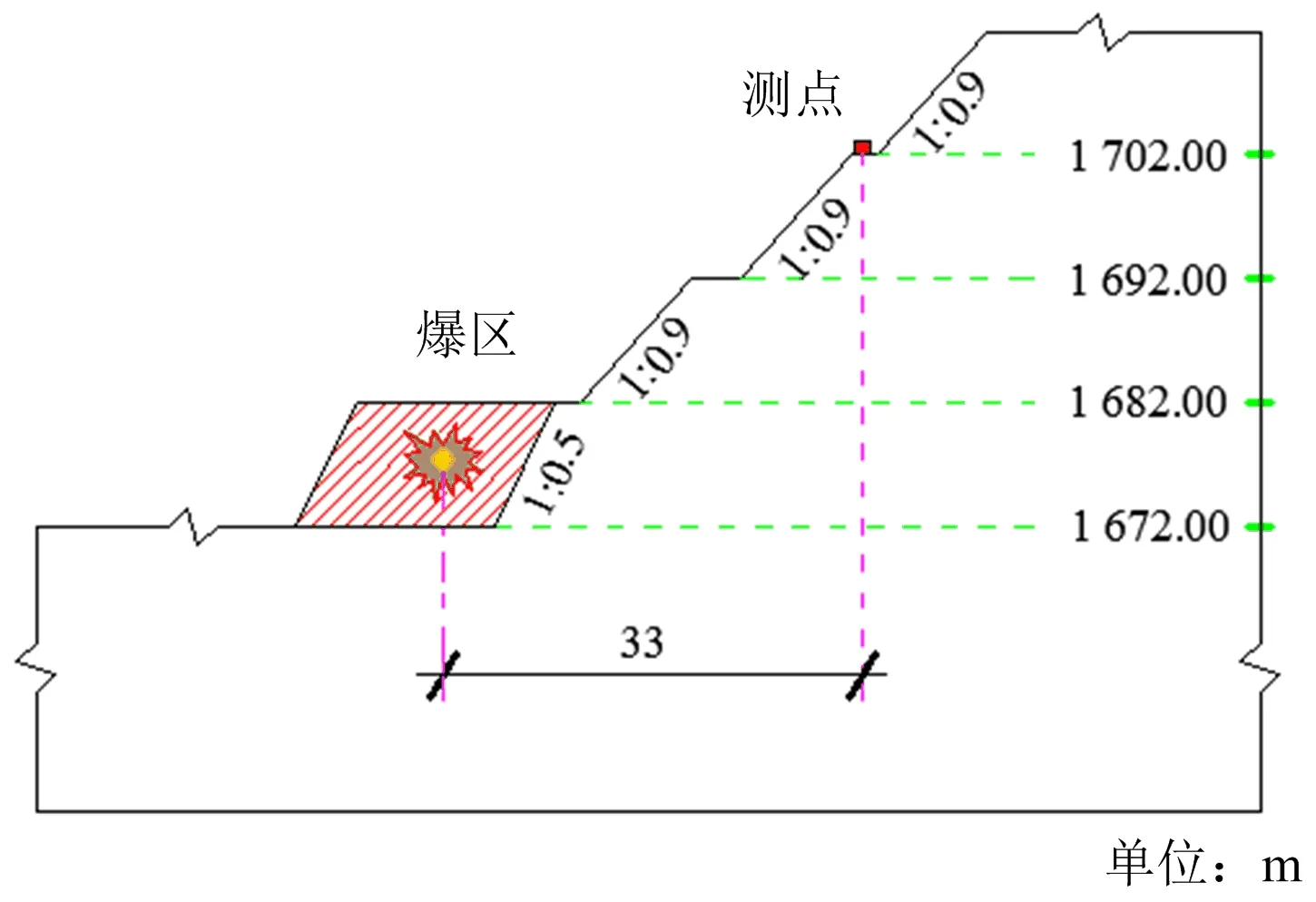
图1 爆破开挖边坡横断面Fig.1 Cross section of slope excavated by blasting

此次爆破开挖采用梅花形布孔方式和2#岩石乳化炸药，炸药单耗q=0.4 kg/m3，密度1.1 g/cm3，炮孔直径90 mm，孔深10 m，超深1 m，填塞3.0 m左右，孔距3.0 m，排距2.5 m。预裂孔间距1.0 m，线装药密度0.5 kg/m。采用逐排起爆网路，最大段药量550 kg。

1.2 爆破振动监测信号

爆破振动信号用TC-4850N型测振仪进行采集，测点布置在爆区上部边坡高程1 702 m台阶平台上，且距离坡顶1 m的位置处，位置确定后，将传感器用石膏固定粘在清理干净的基岩上，以保证监测效果的良好性。采集到的爆破振动信号如图2所示。

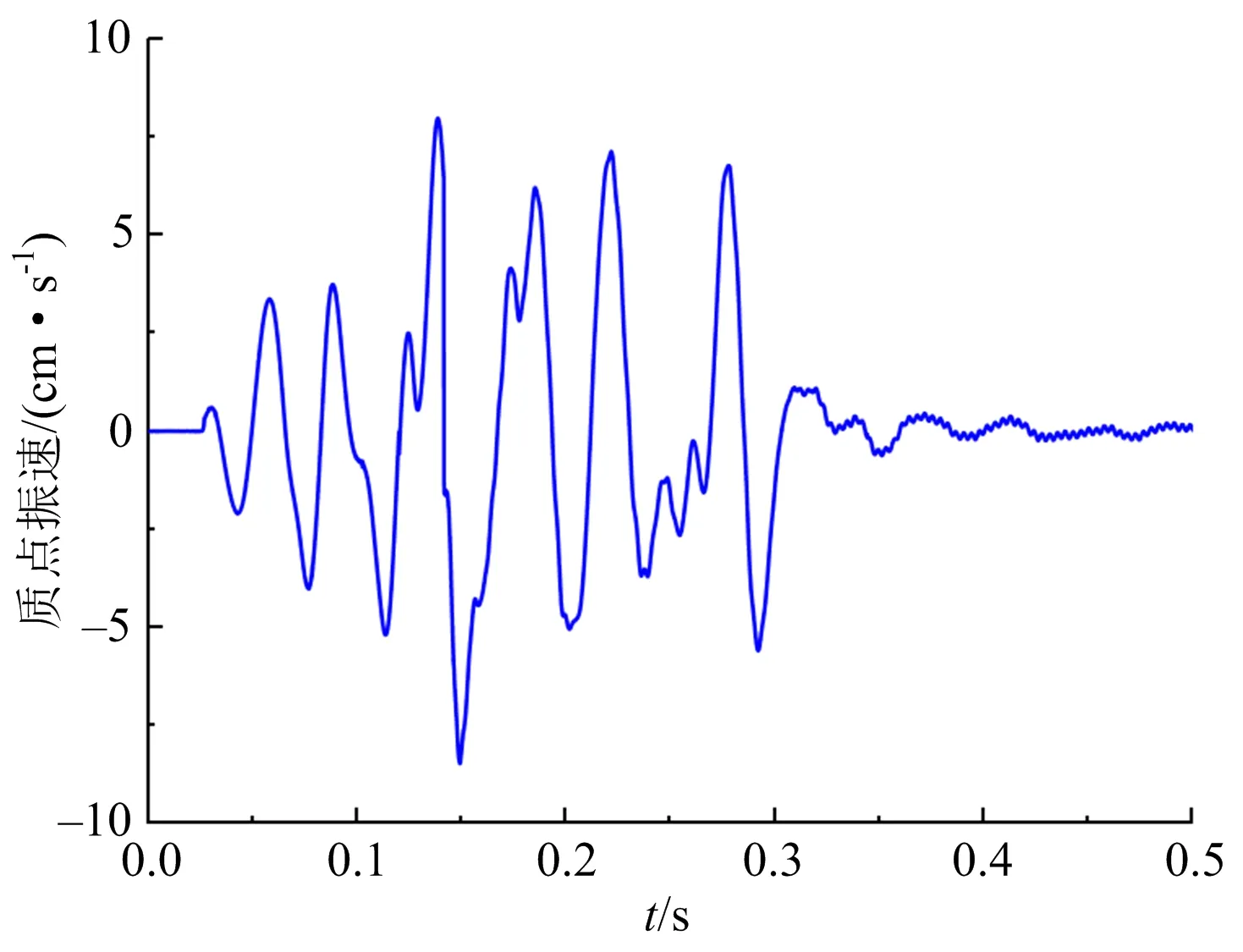
图2 爆破振动监测信号Fig.2 Blasting vibration monitoring signal

2 HHT变换原理

2.1 经验模态分解算法与去噪

HHT分析方法是由Norden E Huang等[16]提出，该方法可针对非平稳随机信号实现对称与平稳化的技术处理，在信号分析领域取得了关键突破。假设有一爆破振动信号，可利用HHT法将此信号通过EMD分解，即可得到若干表征信号的固有模态函数(IMF)，而其中所有IMF都是单分量幅值或者频率调制信号，再对IMF分量通过Hilbert变换处理后获取信号时频和能量分布特征，进而也可局部分析爆破信号在时间与频率中的不同能量分布规律。

为研究如爆破开挖产生的瞬态且非平稳振动信号，频率应该假定为与时间相关的函数，对监测的爆破振动信号进行EMD分解的要求是一步步筛选而获得IMF。IMF是要符合以下假设[17]:①信号数据序列中极值点与零点个数的差值为0或±1；②信号任一点通过局部极大值得到的上包络线与极小值得到的下包络线的均值是0。

EMD分解算法[17]是对监测振动信号X(t)求解其一切极值点，利用三次样条插值函数曲线对极大、小值点各自求插值，拟合得到爆破振动信号X(t)的上、下包络线Xmax(t)、Xmin(t)，再求它们均值线m1(t)为

m1(t)=[Xmax(t)+Xmin(t)]/2

(1)

h1(t)=X(t)-m1(t)

(2)

信号的不一样也许使h1(t)是一个IMF分量，但如若不是，此时应将h1(t)当成原信号重复上述步骤k-1次，则有

hk(t)=hk-1(t)-mk(t)

(3)

根据IMF假设和筛选停止的准则[17]，直到可把hk(t)认为是第一阶IMF，记为c1(t)，残差r1(t)=X(t)-c1(t)，并记为第二次筛选的爆破振动信号，重复n次运算，当cn(t)或rn(t)小于设定误差阈值，或残差rn(t)变成单调函数时，此时分解便终止不再继续。至此，原信号X(t)可由n阶IMF分量和残差rn(t)组成，也就是

(4)

信号经EMD分解得到由各频段构成的信号ci(t)，去除噪声高频信号分量，可组合不同频段的IMF分量实现提取我们所需要的爆破振动主成分信号。

2.2 Hilbert变换与谱

对上述EMD分解的爆破振动信号IMF分量的Hilbert变换：

(5)

式中：PV为柯西主值，构造如下解析信号为

z(t)=c(t)+jH[c(t)]=a(t)ejΦ(t)

(6)

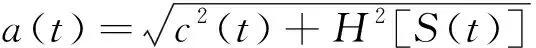
在相位函数的基础上定义瞬时频率为

(7)

IMF分量经Hilbert变换之后，爆破振动信号Hilbert谱可写成：

(8)

式(8)省去了残余函数r，Re为取实部。若H(ω,t)对时间积分，即可得到Hilbert边际谱：

(9)

边际谱表示了爆破振动信号各频率在全局上累加的幅值或能量，同时，可定义Hilbert瞬时能量为IE(t)；实际上，若振幅的平方对时间进行积分，则能获取Hilbert能量谱，再在能量谱基础上定义Hilbert边际能量为E(ω)，两者表达式如下：

(10)

(11)

这里，瞬时能量和边际能量分别提供了信号能量随时间和频率的变化情况。

3 爆破振动信号主成分提取结果分析

3.1 爆破振动信号主成分提取

基于现场爆破振动监测采集的信号(见图2)，采用上述EMD分解算法编制MATLAB程序进行运算，所得的各阶IMF分量呈现出的模态(见图3)，且具有明晰的物理意义，并计算了不同IMF分量能量分布特征如图4所示。

图3 EMD分解后的各阶IMF分量Fig.3 IMF components of each order after EMD decomposition

图4 IMF各阶分量能量分布Fig.4 Energy distribution of each order IMF component

由图3和4可知，监测的爆破振动信号经EMD分解得到c1～c9及余量共计10个IMF分量。一般情况下，这些IMF各阶分量是按局部频带区间由高至低依次排列，研究结果充分说明了EMD分解具有可使信号反映出局部性强的特点；c1分量作为高频噪声，出现在整个信号采集的过程中，其波形震荡密集并表现出高频、低幅值、波长短等特点，是原始信号在复杂环境监测条件下受到噪声干扰的成分，而残余项曲线呈现了振动监测过程中产生的零点漂移与信号偏离基线的趋势，归为振动信号成分中的低频趋势项。c2～c6分量的振速幅值比较大，涵盖了信号的绝大部分能量，该些分量会对周围边坡岩体与建(构)筑物造成一定强度的扰动，不可与其他分量等同视之，而应加大关注；c7～c9分量的爆破振动频率衰减较快，波长也随之拉大，直至降至成微弱的振速和能量。

3.2 爆破振动信号主成分分析

为对爆破振动信号主成分提取后的结果展开研究，在上述对信号经EMD分解得到的IMF分量的前提下，对c2～c9的IMF分量进行重构，得到去噪和消除残余项的主成分信号(见图5)，再通过Hilbert变换能求解爆破信号能量与时间或频率之间的对应关系，得到Hilbert能量谱(见图6)、瞬时能量(见图7)和边际能量(见图8)。

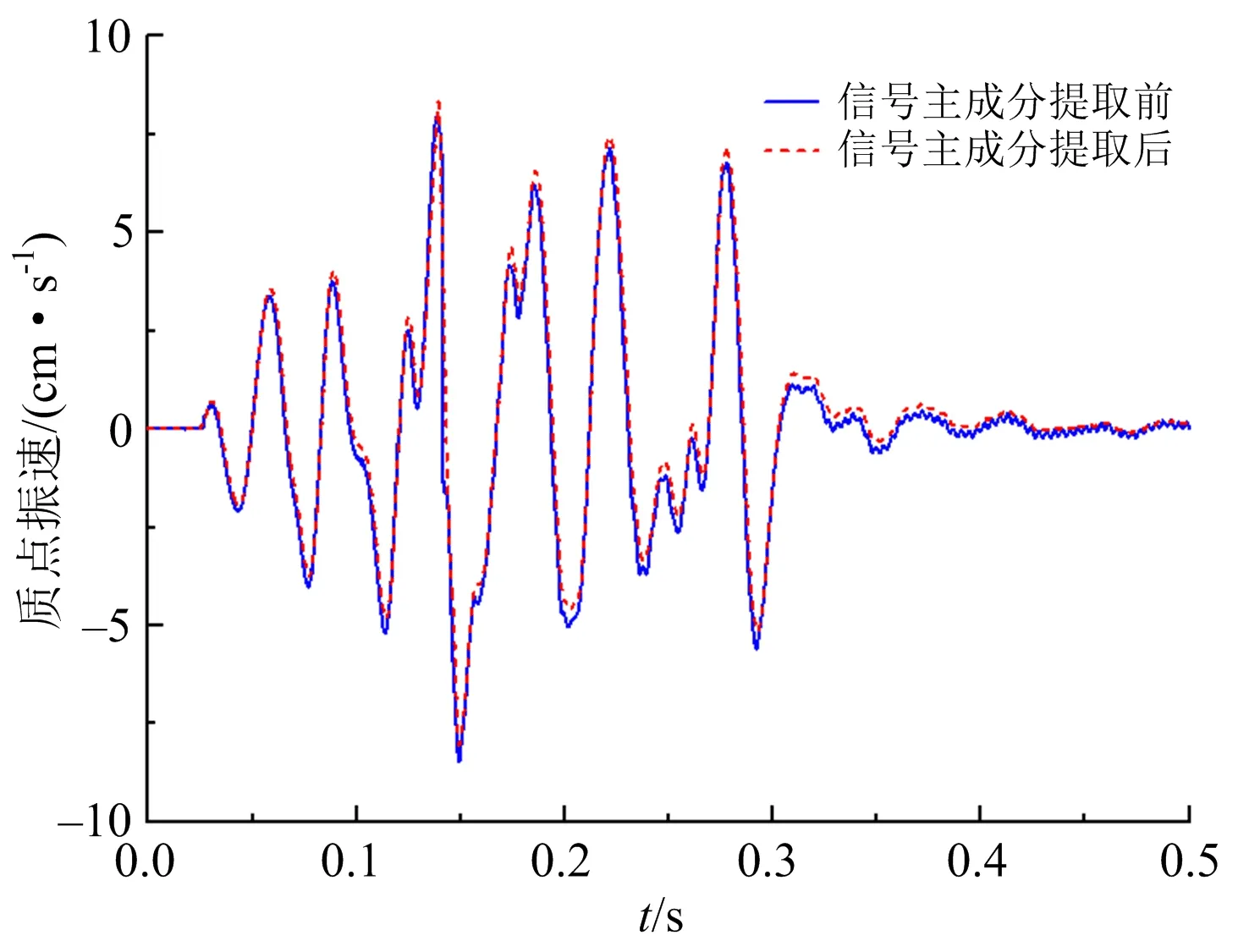
图5 爆破振动监测信号主成分提取后的对比情况Fig.5 Comparison of blasting vibration monitoring signal after extracting principal components

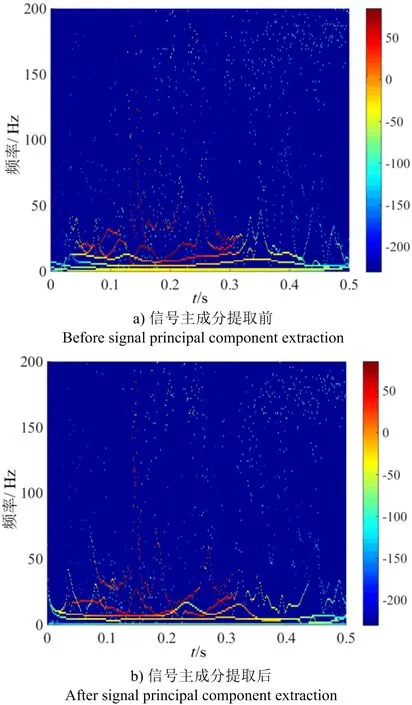
图6 Hilbert能量谱Fig.6 Hilbert energy spectrum

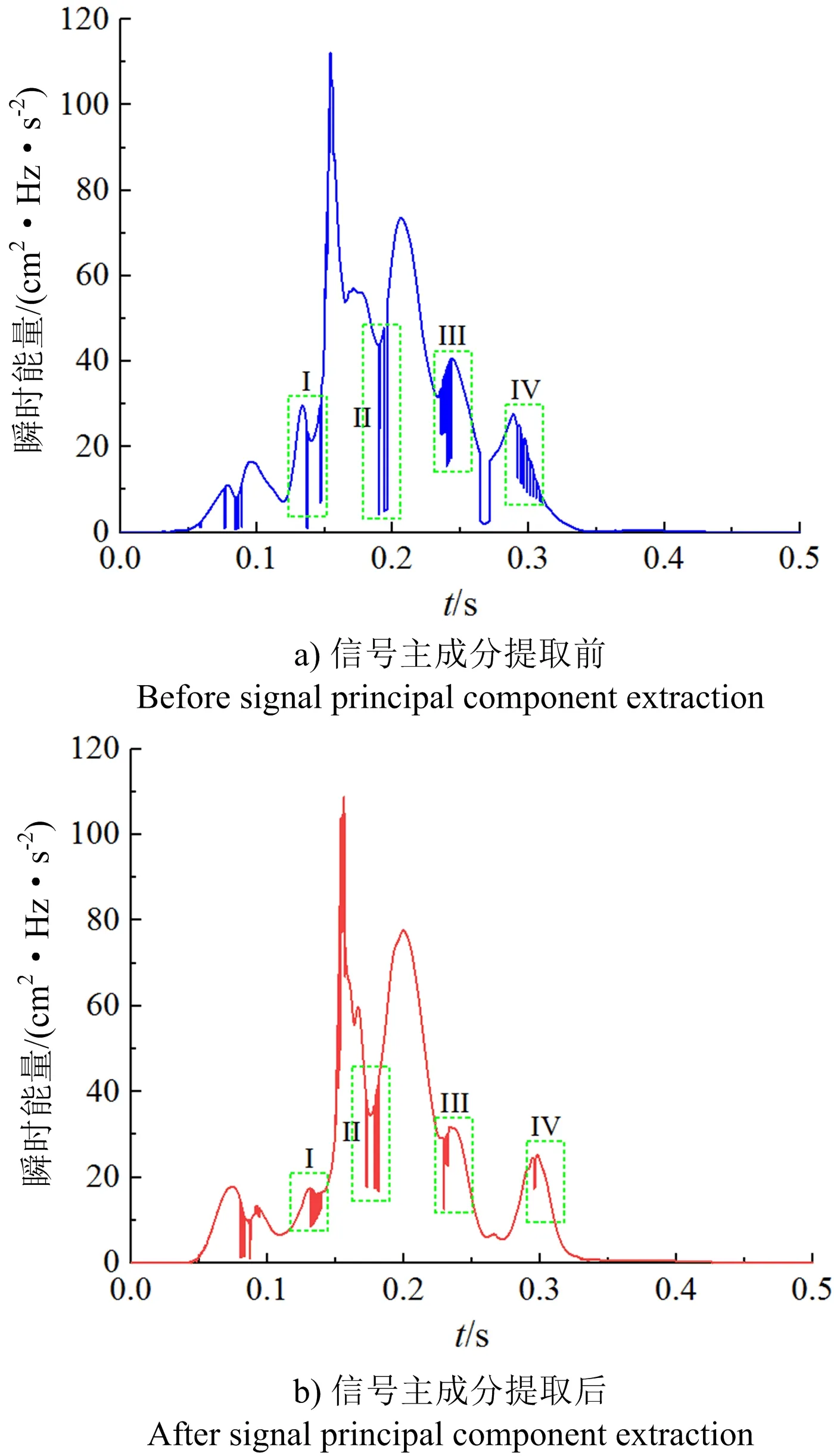
图7 瞬时能量Fig.7 Instantaneous energy

由图5可知，在爆破振动监测信号尾振段有很明显的高频振荡噪声干扰成分，信号主成分提取后的峰值振速变化很小，有效地保留了信号的形态与且曲线光滑性提高，爆破振动信号主成分提取效果比较理想。

由图6可知，岩质边坡爆破振动信号的频率较为丰富，其Hilbert能量谱中偏红色点对应的频率主要集中在60 Hz以下，说明高频分成能量较少；爆破振动信号主成分提取前后的Hilbert能量谱在频率为10 Hz以下的颜色有明显的改变，研究发现提取了爆破振动信号主成分的能量降低了，可以表明是消除了低频趋势项的结果。

由图7可以看出，瞬时能量随监测时间的变化情况，爆破振动信号主成分提取前后的瞬时能量峰值均出现在0.155 s左右，分别为112.12、108.70 cm2·Hz/s2，误差为3%左右，相对较小，研究结果与原始爆破振动信号峰值振速分布规律基本一致；同时信号的瞬时能量主要集中在0.1～0.3 s，结果和图2的监测波形或图6的Hilbert能量分布情况一样，有良好的对应效果；爆破振动信号主成分提取前的瞬时能量在I，II，III，IV处的光滑性较差，经过去噪和消除趋势项的处理之后，即信号主成分提取后的瞬时能量在I，II，III，IV处的光滑性有一定的改善，其曲线整体过渡性光滑度有所提高，信号主成分的提取效果良好。

由图8可知，信号主成分提取前后边际能量在频段内有一些波动，但它们都主要集中在60 Hz以下，爆破振动信号主成分提取后的频率分布稍有变窄，且在10 Hz以下的边际能量显著降低，与Hilbert能量谱的分析结果一致。

图8 边际能量Fig.8 Marginal energy

因此，在分析和评估边坡岩体爆破开挖产生的振速和能量时，我们应充分考虑并对信号高频噪声与低频趋势项进行剔除，获取爆破振动信号主成分，可提高信号的局部时频特征，以准确评估建(构)筑物的爆破振动，并为保证爆破施工安全与边坡稳定提供参考依据。

4 结论

1)EMD分解的各阶IMF分量在局部频带区间从高到低依次排列，呈现出一定尺度范围的模态，具有明晰的物理意义，去除高频噪声和低频趋势项可以实现爆破振动信号主成分的重点提取。

2)Hilbert能量谱能直观体现信号能量与时频之间的关系，信号能量主要在60 Hz以下的低频段和0.1～0.3 s的时间段，爆破振动信号主成分提取前后的瞬时能量峰值分别为112.12、108.70 cm2·Hz/s2，相对误差较小。

3)提取主成分后的爆破振动信号频率分布稍有变窄，且在10 Hz以下的边际能量显著降低，而瞬时能量和振动速度曲线整体过渡性光滑度有所提高，信号主成分提取效果良好。因此，在分析边坡岩体爆破开挖产生的振速和能量时，获取爆破振动信号主成分，可提高信号的局部时频特征，以准确评估建(构)筑物的爆破振动，并为保证爆破施工安全与边坡稳定提供参考依据。