某小型客车侧翻简化模型关键结构优化设计

莫易敏，刘青春，高 烁，吕俊成

（1.武汉理工大学机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545007）

1 引言

近年来，虽然在汽车事故中侧翻所占的比例并不大，但侧翻的死亡率高达正面、侧面碰撞的6倍［1］。相比正碰、侧碰事故，在侧面翻滚事故中，车体变形更大，严重侵入乘员生存空间，导致侧翻对乘员的伤害程度远大于其他几种事故［2］。因此对侧翻生存空间侵入量的研究对降低乘员伤害程度具有重要的社会和经济意义。

由于对整车侧翻性能的影响规律研究需要大量数据支撑，若对整车有限元模型进行多次修改计算的工作量巨大，进行仿真求解耗时过长，无法获取大量数据，因此用原始有限元仿真方法不适合研究车身关键结构对整车侧翻性能的影响。因此需要建立简化模型，大大缩短仿真计算时间，有利于研究侧翻关键结构对侧翻性能的影响及优化。

近些年，文献［3］对客车的车身局部段进行研究，在结构变形量最大的部位采用外部加强结构，增强客车侧翻安全性能，但存在局限性，需要根据车辆实际结构情况制定方案，处理复杂。文献［4］通过选择不同的材料进行侧翻安全性研究，研究结果表明，客车的被动安全性的高低与车身上部结构的屈服极限呈正相关性。上述主要研究侧翻结构或者材料单一因素，针对多因素的优化分析较少。综上提出以A柱、B柱、上边梁的厚度和材料作为研究对象，采用拉丁超立方对三者厚度和材料六个设计变量抽样，根据每组样本点对侧翻简化仿真模型进行修改并提交计算，以最大侵入量和总质量为设计目标，获取25组样本点，构建Kriging近似模型，运用非支配排序遗传算法NSGA-Ⅱ进行多目标优化，并得到计目标的Pareto前沿。将所得的优化方案中各参数带入有限元模型进行仿真计算验证，最终在提升侧翻安全性的同时兼顾了轻量化。

2 侧翻试验设计与对标

2.1 试验设计

按GB/T 17578《客车上部结构强度》法规：客车整车侧翻试验，如图1所示。车身锁止于侧翻平台上，距离地面的高度差为800mm，在整车轮胎处一侧放置限位挡块，限制侧翻过程中车辆侧向滑动，挡块高度不得超过侧翻车辆轮辋部位与翻转平台表面间距离的2/3，长度最小值为500mm［5］。

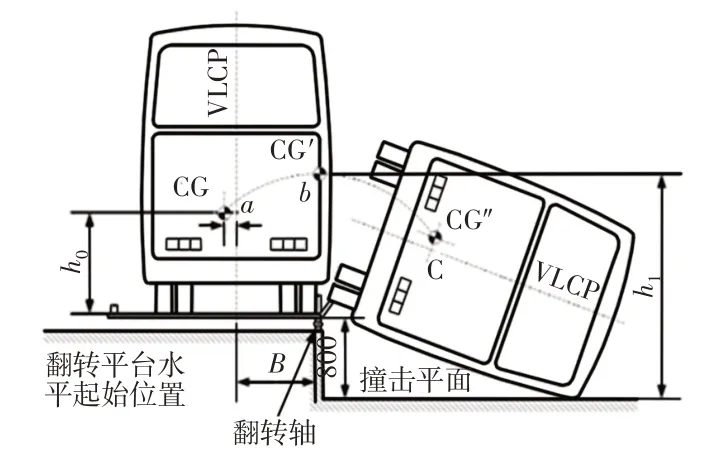
图1 客车整车侧翻试验示意图Fig.1 Schematic Diagram of Passenger Car Rollover Test

试验过程：侧翻试验采用的是副驾驶侧着地，以车轮和翻转平台接触平面为旋转轴，平台绕轴缓慢旋转升举车辆至临界失稳位置，初始角速度为0.078rad/s，旋转过程角速度不超过0.087rad/s（5°/s），在重力作用下绕转轴运动，翻转至干燥且平整的水泥地面，在客车开始翻滚至临界失稳位置期间不能产生晃动和动态效应［6］。图1中ɑ点为客车在翻转平台水平起始质心高度位置，b点为临界失稳状态位置，c点为触地瞬间位置。

2.2 有限元模型的建立

2.2.1 有限元模型的设计方案-能量守恒

根据能量守恒定理，在忽略空气阻力等影响因素前提下，整车在临界点的动能与势能和在触地瞬间的总能量是相等的，此时轮胎与挡板脱离为非接触状态［7］，计算公式见式（1）～式（5）：

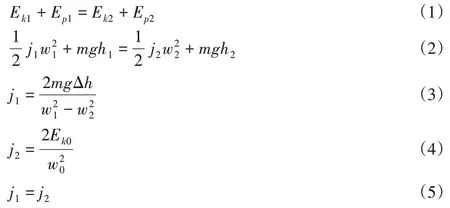
式中：Ek1和Ep1—整车在临界失稳（图1中b点）位置的动能和势能；Ek2和Ep2—整分别是车在触地瞬间（图1中c点）位置的动能和势能；j1和j2—整车分别在b点和c点处的转动惯量；w1和w2—整车分别在b点和c点处的翻转角速度；h1和h2—整车在b点和c点处质心距离地面的高度；w0—整车初始翻转角速度，可以为任意值，选取w0与w1相等。

注释：w1必须满足法规要求，不大于0.087rad/s，w0在提交模型计算一个时间步长后在结果AST文件中获得。

从临界失稳到触地瞬间的侧翻时间大约占所有非碰撞时间的（60～75）%，此过程车身基本无任何变形发生，能量守恒方案简化此段侧翻过程，可以极大节省模型计算时间，仿真效率有很大提升，有利于获取优化侧翻关键结构前的大量抽样数据，同时对侧翻结果的影响不大。

2.2.2 有限元模型的建立

在建立侧翻简化模型钱，首先将UG中构建的整车模型导入软件HYPERMESH中，在保证精度的前提下，适当简化模型，合理设置网格大小，设置侧翻模型中关键结构的网格尺寸为8mm，如A柱、B柱、上边梁等，其他尺寸为10mm。赋予所需材料和属性，定义COMPONENT间连接和接触，由于翻转初始角速度不得超过0.087rad/s（5°），选取初始角速度为8.7e-05rad/s，构建整车的原始有限元模型［8］。在LS-DYNA中提交计算，与试验进行对比验证仿真模型的准确性，获取整车原始模型在触地瞬间时整车模型XYZ方向平动和转动的速度、加速度等运动参数。

其次调整整车模型初始状态为整车原始模型运动到触地瞬间时的状态，并将获取的运动参数赋予给整车简化模型，保证整车简化模型与原始模型的翻转角度、速度、加速度，之整车质心坐标等相同，实现无碰撞过程的简化，利用“Load Collectors”加载设置功能中“InitiaVel”（*Initial Velocity Generation）类型加载便可实现初始状态设置，最后将整车简化模型提交计算。侧翻有限元模型，如图2所示。侧翻整车原始模型初始状态，如图2（a）所示。简化模型初始状态，如图2（b）所示。

图2 侧翻有限元模型Fig.2 Flip Finite Element Model

根据法规，建立生存空间，以SR为基础点，网格尺寸设置为50mm，采用Xtranode将其与车内底板连接，施加与整车一致的翻转工况，法规中生存空间示意图，如图3（a）所示。生存空间模型示意图，如图3（b）所示。

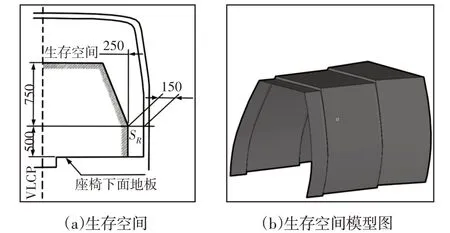
图3 生存空间示意图Fig.3 Schematic Diagram of Living Space

将侧翻模型控制卡片中Termin的ENDTIM由原来的3000缩减为1500，使得计算时间大大缩短，相比原始仿真模型仿真效率提升47%。

2.3 评价指标

为了更好更方便研究侧翻的安全性，侧翻试验主要从以下两个方面进行评判：最大侵入量L表示侧翻整个过程中车体结构向车内的最大侵入量，反映的是侧翻过程中生存空间是否会被侵入。侧翻关键结构最大侵入量测量点，测量点主要涉及A柱（A1-A11点）、B柱（B1-B5点）和上边梁（M1-M6点）部分，如图4所示。试验前，除了标记A、B以及上边梁外板等，还对A、B、C、D柱以及上边梁外板和B柱内板、车门进行变形点标记，利用三坐标测量仪进行各标记点的坐标测量，与试验后数据对比得到各标记点变形量。同时随着人们环保意识的提升，汽车油耗性能要求也愈发严格，轻量化也成为车身结构设计中的重要课题［9］。因此有必要将质量Mass作为评判标准之一。

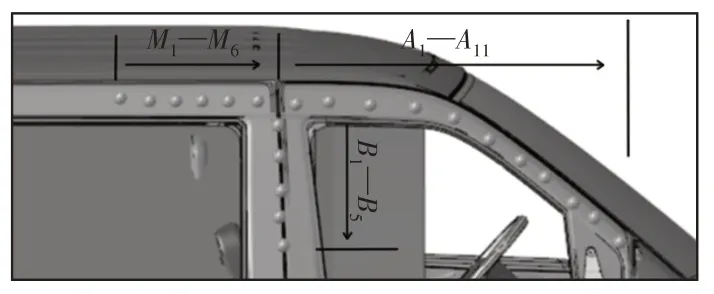
图4 最大侵入量测量点Fig.4 Maximum Intrusion Measurement Point

2.4 侧翻试验与有仿真简化模型对标

2.4.1 关键结构

试验与仿真结果表明，侧围上端和车顶左侧连接处受挤压变形严重，生存空间被侵犯。将仿真模型与试验整车进行对比分析，结构变形对比，如图5所示。侧翻挤压变形一致，如图5（a）所示。关键结构A柱、B柱、上边梁中段受到变形，位置相同，验证了模型的可靠性，如图5（b）、图5（c）所示。说明生存空间受到侵入，如图5（d）所示。

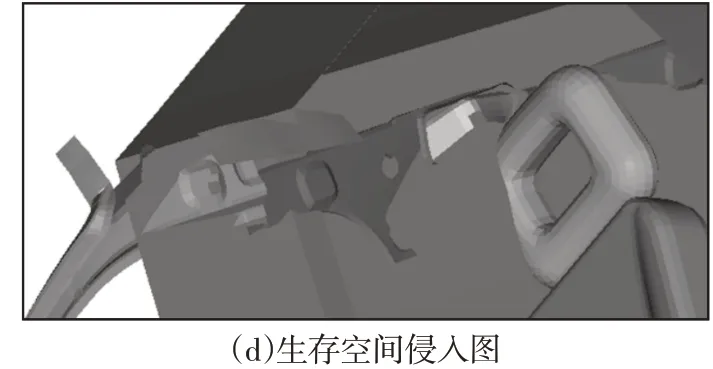
图5 结构变形对比Fig.5 Structural Deformation Comparison

2.4.2 最大侵入量

在客车侧翻过程中，最大侵入量是最直接判断生存空间是否被侵入的评价指标，也是验证试验与仿真模型变形一致性的标准。侧翻关键结构主要为A柱、B柱和上边梁，试验中最大侵入量为158.658mm，仿真中为153.523mm，试验与仿真模型误差在±7mm之内，仿真模型准确，如表1所示。

表1 试验与仿真关键结构最大侵入量对比Tab.1 Comparison of Maximum Intrusion of Key Structures in Test and Simulation

3 基于Kriging近似模型的侧翻关键结构优化

3.1 侧翻关键结构多目标优化问题

将A柱、B柱和上边梁作为侧翻关键部件作为研究对象，以A柱材料M1、厚度t1；B柱材料M2、厚度t2；上边梁材料M3、厚度t3作为侧翻耐撞性优化问题的六个设计变量，确定各设计变量取值的选取范围，如表2所示。

表2 设计变量取值选取范围Tab.2 Design Variable Value Selection Range

侧翻关键结构优化问题属于耦合问题，在增强耐撞性的同时不增加质量，由于设计目标相互影响以及目标函数的连续性，找不到绝对最优解和所有非劣解，但是可以根据由非劣解组成的Pareto前沿寻到相对最优解。构建多目标优化的数学模型见式（6）：

式中：Mɑss—A柱、B柱、C柱三者总质量；Lz—Z方向最大侵入量；—A柱、B柱、上边梁厚度取值上下界，其中—0.6mm、1.0mm—1.0mm、1.4mm—1.0mm、1.4mm；Mi—选取5种常见材料，如表2所示。

3.2 拉丁超立方试验抽样

拉丁超立方是在约束条件下随机且均匀生成样本点的试验设计，具有拟合非线性响应等优点。在建立准确的近似模型，选取六个设计变量组成的样本空间进行采样，得到25组样本点数据。根据样本点修改整车侧翻关键结构对应属性和材料，并使用LS-DYNA计算修改的25组模型，得到对应样本点A柱、B柱、上边梁最大侵入量L和三者质量之和Mass。正交试验设计与优化目标对应值部分列举，如表3所示。其中，0组数据为初始数据，用于与优化结果对比，获取最优结果

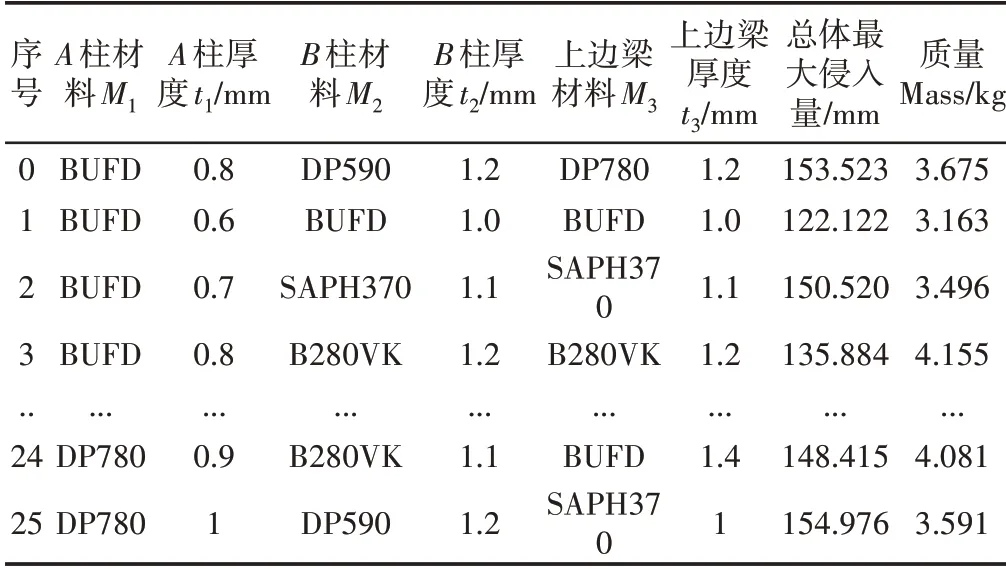
表3 拉丁超立方抽样Tab.3 Latin Hypercube Sampling

3.3 Kriging近似模型

客车耐撞优化属于高度非线性问题，Kriging可以在约束区域内对区域化变量进行无偏最优估计，不依赖随机误差的存在，能在高度非线性情况下拟合较高精度的近似模型。根据表3中25组样本数据构建Kriging近似模型，近似模型误差评价指标有：

相对平均绝对误差（Average）、最大绝对误差（Maximum）、均方根误差（Root Mean Square）和确定性系数（R-Squared），前三项评价指标数值越小、同时最后一项评价指标数值越接近1代表模型精确性越高［10］，如表4所示。以上四项精度指标默认可接受范围分别为：（0～0.2）；（0～0.3）；（0～0.2）；（0.9～1.0）；由表4可知，构建的Kriging近似模型的误差均在可接受范围内，该近似模型可以用于A柱、B柱、上边梁优化分析。

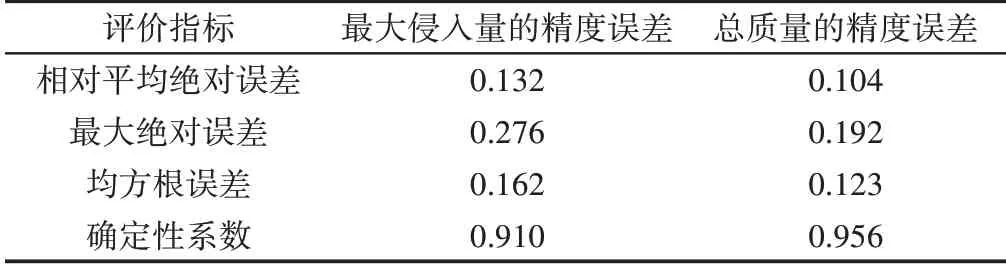
表4 近似模型误差分析Tab.4 Approximate Model Error Analysis

3.4 NSGA-Ⅱ算法优化

多目标遗传算法NSGA-Ⅱ在NSGA算法基础上引入了精英策略，对共享变量进行改进，降低计算消耗，解决在高维问题中收敛速度慢甚至难以收敛问题［11］。

在多目标优化过程中，将优化问题转化为确定关键结构厚度和材料为最佳组合时使得侧翻试验中总体最大侵入量最小，又满足轻量化要求。采取NSGA-Ⅱ算法对Kriging近似模型进行优化计算，得到由非劣解集构成的500次迭代Pareto前沿并趋于稳定，如图6所示。利用最小距离法选取一个相对最优解，选取对应的设计变量为：A柱厚度0.6mm，材料4，B柱厚度1.1mm，材料4，上边梁厚度1.2mm，材料5。

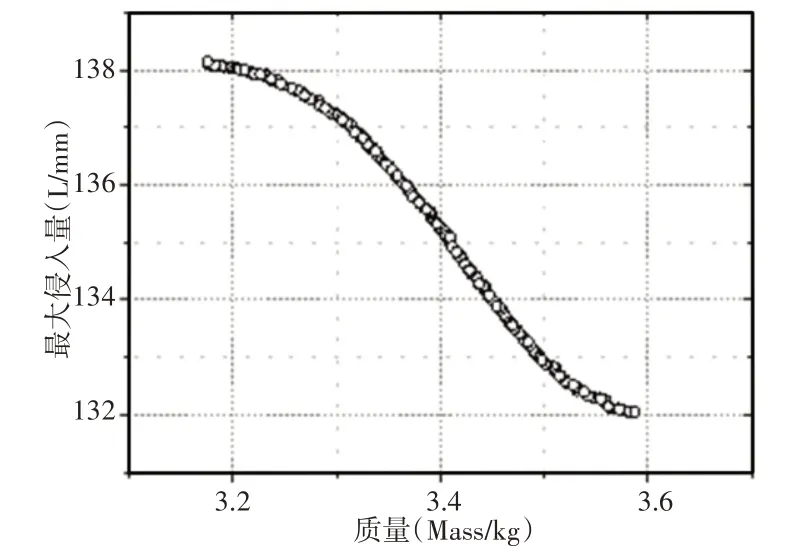
图6 500次迭代Pareto前沿Fig.6 Pareto Frontier of 500 Iterations

3.5 基于有限元简化模型的结果验证

将优化后的设计变量代入侧翻简化模型并提交计算，如图7所示为整车关键结构挤压结果对比，改进之后侧围上端的变形明显减小、生存空间未受到侵犯，整车最大变形变形量由最初的153.523mm减小到132.05mm，总质量由3.675kg减小到3.508kg，满足了GB17578-2013国标要求和轻量化要求。

图7 结果验证Fig.7 Results Verification

4 结论

（1）在研究整车侧翻时，忽略试验过程中空气阻力，轮胎与地面摩擦力等因素的前提下，整车能量守恒，即在临界点的总能量与触地瞬间总能量相等，将侧翻简化模型原始状态调整为原始模型在触地瞬间时的状态，并代入对应的几何参数，使得侧翻简化模型从触地瞬间开始计算，节省了原始模型从临界点到触地点的翻转时间，大大提高仿真计算效率，同时模型仿真难度没有增加。提出的简化侧翻方案对提高侧翻仿真效率提供参考。

（2）以A柱、B柱、上边梁的材料和厚度为设计变量，以最大侵入量和总质量为设计目标，构建近似模型进行优化，获取满足GB17578-2013国标要求兼顾轻量化要求的相对最优解。优化结果表明，整车最大变形变形量由最初的153.523mm减小到132.05mm，总质量由3.675kg减小到3.508kg。所提出的优化方案对提高侧翻安全性提供参考。