应用SVM算法的相位—三维坐标标定方法

张 瑞，王亚龙，张伟豪，朱振伟

（郑州大学机械工程学院，河南 郑州 450001）

1 引言

在智能产线中，为便于进行质量跟踪进行，对所有工件逐一分拣，进行工序间检测是基础要求。国内外现有的分拣技术多通过视觉系统，对每个工件进行定位，再通过机械臂抓取每个工件［1］。已有视觉系统多采用立体视觉技术，如双目视觉技术［2］、结构光三维测量技术等。需要确定每个毛坯工件的空间位姿，且对定位精度有极大的要求。故采用不易受外界条件影响、定位精度更高的光栅投影视觉系统。

光栅投影立体视觉技术对目标物体进行三维重构，关键点即为标定目标物表面特征点的相位与三维坐标的映射关系，其对系统的精度、工作效率等有很大的影响，受到了很多研究人员的关注，但已有的相位高度映射关系研究有以下问题：（1）有的光栅投影视觉模型采用建立显式函数或者隐式表达式的方式求解映射关系，涉及到采用大量数据来近似拟合公式中的系数，计算过程中都会引入标定中累积的误差［3］。（2）有的标定模型中，引入LUT查找表的方法，需要预先计算查找表中的每个像素对应的值，预处理工作量提高，且计算精度也会受到影响。（3）有的相位高度标定过程中，使用高精度标定量块和精密平移台的辅助，增加了标定成本，降低了标定的效率。（4）国内外已有的通过神经网络方法，对相位高度映射关系进行标定中，隐含地使用了样本无穷多的假设条件。使用该方法需要采集大量的数据，提高了数据处理量，降低了效率［4-5］。

根据工程要求通过视觉方法求得目标物体上特征点的精确位置，即其在相机坐标系下的三维坐标。同时为了避免以上已有光栅投影视觉系统中的问题，现提出一种基于相机坐标系与投影仪坐标系空间关系，及相位与三维坐标的非线性映射关系，并应用小样本、高效率的SVM算法，建立空间点相位—三维坐标映射关系的标定模型，并通过实验验证该标定模型的有效性以及精度。

2 视觉系统模型

根据实际应用搭建的，单目相机与投影仪组合成的视觉系统结构示意图，如图1所示。调节单目相机与投影仪在工作台上有公共视野，它们相对位置没有严格要求，只需保证相对位置固定即可。图中所示工作台上坐标系O-XYZ由相机和投影仪公共视野确定，可根据工程实际情况调节位姿。用物块等效替代在物料框中的某一毛坯工件。

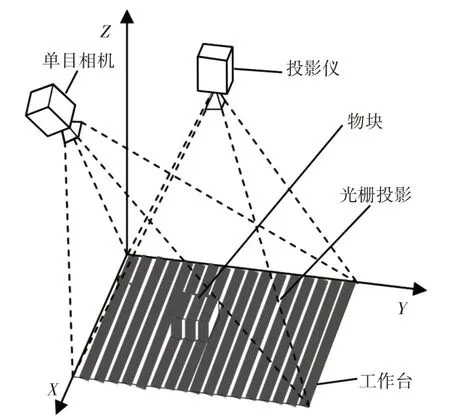
图1 光栅投影的视觉系统结构示意图Fig.1 Visual System Structure Sketch of Grating Projection

设相机与投影仪的镜头畸变、外界环境因素的影响都不存在，可有如下理论计算分析：

图1中单目相机拍摄表面有正弦条纹的目标物，条纹由投影仪投射在工作区域平面上。通过建立相机和投影仪坐标系，可得光栅投影视觉系统的空间坐标系示意图，如图2所示。

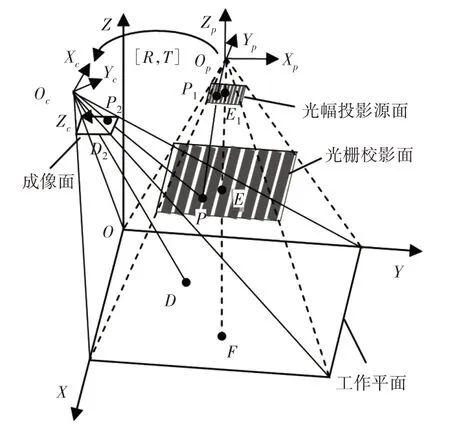
图2 光栅投影视觉系统空间坐标系示意图Fig.2 Grating Projection Vision System Space Coordinate System Diagram

单目相机与投影仪的位置固定，它们之间的位置关系也唯一确定，相机与投影仪坐标系之间的转换矩阵可以表示为［R3×3，T3×1］。假设相机坐标系为Oc-XcYcZc，相机光轴OcD交成像面于D2点，交工作面于D点；投影仪坐标系为Op-XpYpZp，投影仪光轴OpE交光栅投影源面于E1点，交空间中与由源面投射的、且与之平行的光栅投影面于E点，交工作平面于F点，因工作平面与光栅投影面实际上都是空间中的虚拟平面，可设投影仪坐标系Yp轴、工作平面X轴与光栅条纹平行。由上图2可得，空间中某一点P可以看作是相机发射的射线与光栅平面的交点，即两个坐标系下的公共点，OpP交成光栅投影源面于P1点，OcP交成像面于P2点。而点P在两个坐标系下的坐标值可通过转换矩阵［R3×3，T3×1］进行转化，该矩阵具体表达，如下式（1）所示。投影仪坐标系下点P（xp，yp，zp），其在相机坐标系下坐标值可以表示为（xc，yc，zc），两者关系可以用下面式（1）表示。

式中：R3×3—两坐标系坐标值转换的旋转矩阵；T3×1—平移矩阵，两矩阵中的元素在相机与投影仪安装固定之后，即为确定值，可通过标定得出。由图2可得投影仪坐标系下空间点分布，如图3所示。

图3 投影仪坐标系下空间点分布Fig.3 Spatial Point Distribution in Projector Coordinate System

光栅投影源面就是存于投影仪中的、已知相位与尺寸信息的正弦光栅图像。投影仪坐标系下的空间可以分成若干层相互平行的光栅平面，每一层都可看作由光栅投影源面投射出来。同时也可理解为从投影仪原点发射出无数条射线，通过透镜成像。光轴上线段OpE1即为投影仪焦距，长度为fp，设点P，E，P1，E1在投影仪坐标系中的坐标值分别为（xp，yp，zp）、（xe，ye，ze）、（xp1，yp1，zp1）、（xe1，ye1，ze1），各点相位分别为θp、θe、θp1、θe1，则有xe＝ye=xe1=ye1=0，zp1=ze1=fp，zp=ze。

连接P、E两点，得PE垂直于投影仪光轴，连接P1与E1两点，可得PE与P1E1平行，则△OpEP∽△OpE1P1，由三角形相似原理，空间点P的相机坐标值与投影源面中的P1的坐标值具有一定的比例关系，每一层光栅平面都与原始图像都是按照一定比例放大，线段长度具有一定的相似比。则可得如下式（2）。每一层光栅平面上，由于光栅条纹方向平行于投影仪坐标系的Yp轴，故任一条纹上相位相等，则同一光栅投影平面上P与E点的相位与横坐标应满足具有线性关系，根据正弦光栅投影性质，由投影仪投射出的任一条射线上各点的相位相等，可得式（3）。

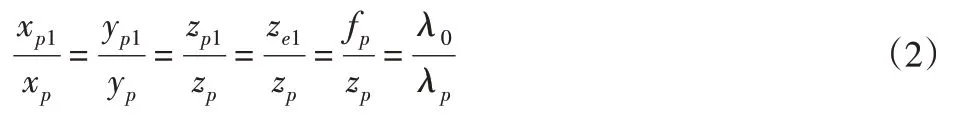
式中：λ0—光栅源平面上的光栅节距，即每个周期的长度；λp—光栅投影平面上的节距，它们的也保持比例关系。

式中：θp1与θp—一条射线上两点P与P1的相位，故它们相等；θe1与θe—同理相等。

联立式（2）、式（3）式可得式（4）。

式中：fp—投影仪的固定焦距；θe—光栅源面中心的相位，可得在投影仪坐标系下，空间任意一点P的坐标值xp，zp与相位θp之间符合该式非线性关系［6］。

由图2可得下图4所示，相机坐标系从原点发射出无数条射线，通过透镜成像，线段OcD2即为相机焦距，长度为f，点D2、P2在成像面坐标系中的坐标分别为（u0，v0），（u，v）；点P，P2在相机坐标系下坐标值分别为（xc，yc，zc）、（x，y，f）。

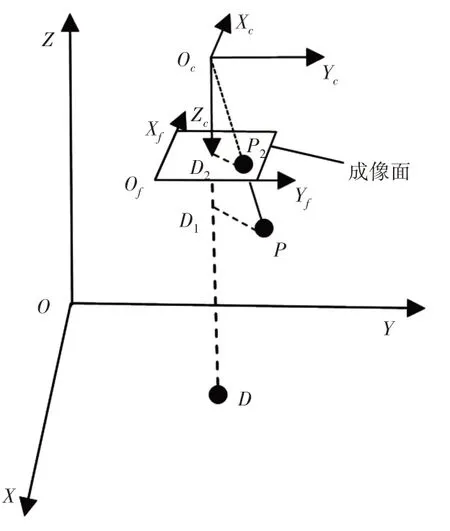
图4 相机坐标系下空间点分布Fig.4 Spatial Point Distribution in Camera Coordinate System

过点P做光轴的垂线，交于D1点，连接P2与D2两点，得PD1与P2D2平行，则△OcD2P2∽△OcD1P，同样，根据投射原理及三角形相似原理，空间点P的相机坐标值与成像面中的P2的坐标值具有一定的比例关系，可得如下式（5）。

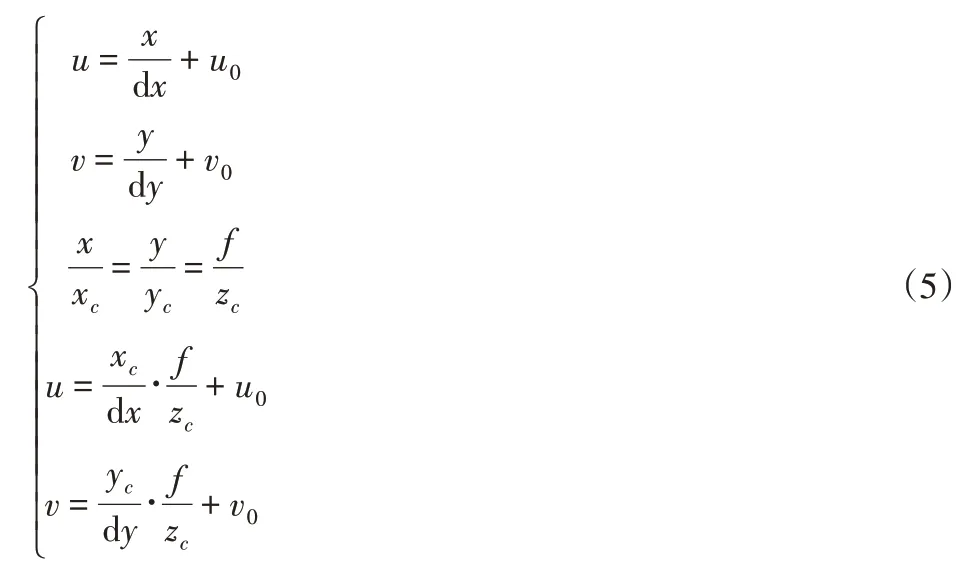
式中：u，v；u0，v0—P2、D2点在成像面坐标系下的横纵坐标值，单位为像素，dx，dy—每个像素在相机坐标系中Xc轴与Yc轴上的尺寸，均为相机的内参。

通过上面分析，综合式（1）、式（3）、式（4）即可得到如下的方程组（6）。使用xc，zc表示xp，zp。即可以将投影仪坐标系下的xp，zp与θ的关系转化在相机坐标系中，得到xc，zc与θ之间的关系。

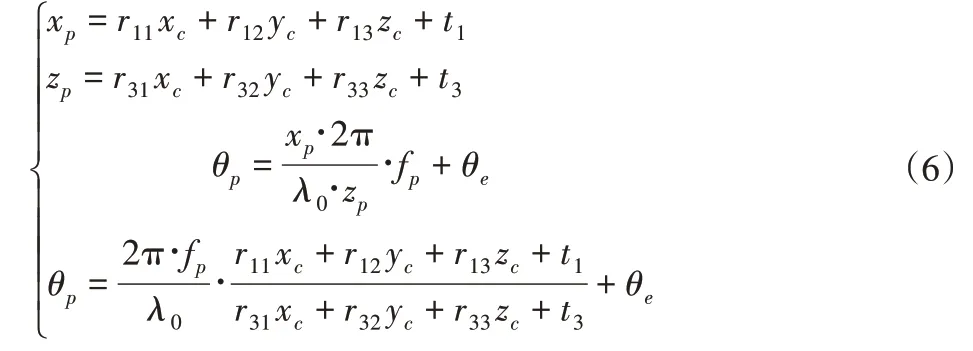
通过上面方程组与式（5）联立，即可得到（u，v，θ）与（xc，yc，zc）之间的映射关系，如式（7）所示。

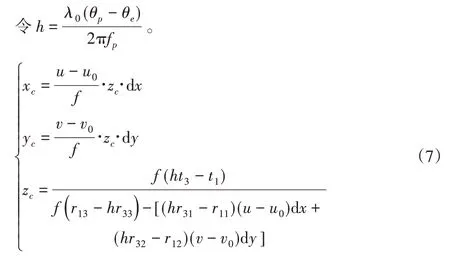
其中，可通过相机采集的图像可得到像素坐标（u，v），空间任意一点相位θ可通过求解绝对相位得到，相机焦距f、投影仪fp、光栅投影源面的节距λ0、相机光轴上点的图像坐标（u0，v0）等系统参数，旋转矩阵中的元素r11、r12、r13、r31、r32、r33，平移矩阵中的元素t1、t3可以通过Zhang氏标定法结合OpenCV工具库进行求解，现有算法可达到亚像素级精度。

上述标定模型是采用理想的数学模型，忽略了一些实际的影响因素，如上述光栅视觉系统中，相机与投影仪由于环境因素产生的畸变等，均不能很好的消除。这给标定工作带来了很大的不便，同时大大降低标定精度。因此对相机—投影仪视觉系统进行标定时，针对摄像机以及投影仪标定过程中复杂的成像和畸变模型，提出了基于SVM算法的光栅投影相位—三维坐标标定模型［7-9］。

3 SVM标定模型建立

根据上面分析，可得空间中任意一点P在图像中P2坐标（u，v）、绝对相位θ与其在相机坐标系下的三维坐标（xc，yc，zc）存在复杂的非线映射关系。SVM是一种有坚实理论基础的小样本学习方法，可以逼近任意复杂的非线性系统，利用SVM算法的学习功能，可以在图像坐标、空间点相位和三维相机坐标之间建立非线性映射模型，且不受任意位姿的物体的表面复杂度的影响；在建立相机图像和投影仪图像对应关系时，算法中自动补偿了投影仪非线性引起的相位误差，对光栅图像的正弦性要求不高，稳定性强。

将相位—三维坐标映射关系标定问题转化为SVM回归问题，其基本思想是通过一个非线性映射φ，将数据x映射到高维特征空间D，并在这个空间进行线性回归。如下式（8）所示［10-11］。

式中：b—阈值；ω—权向量。采用ε不敏感损失函数，对应的支持向量机采用ε-支持向量机，通过对其约束优化问题，引入拉格朗日函数，转化为对偶问题并进行求解，可得对应的SVM回归模型：

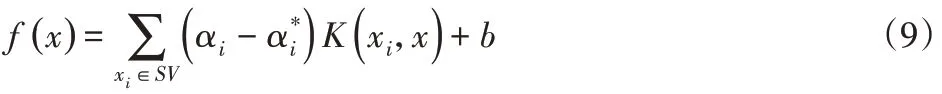
其中径向基函数：

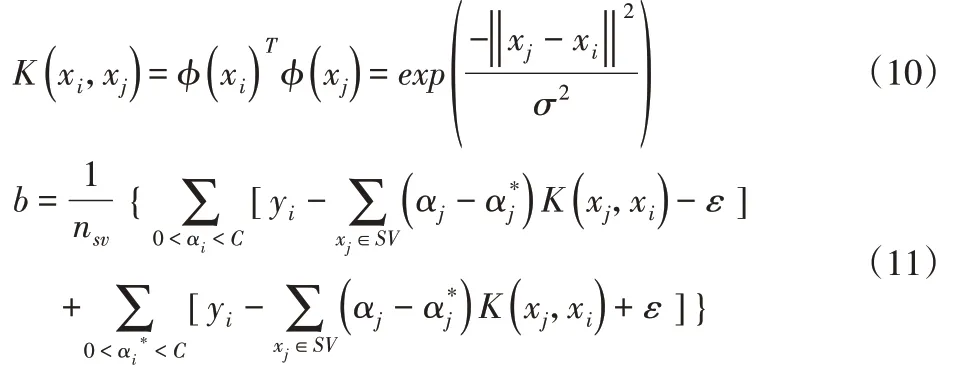
式中：σ2—核密度参数；αi，（i=1，2，…l）—拉格朗日乘子；αi只有一小部分不为0，对应的样本就是支持向量（Support Vector，SV）；nsv—支持向量的个数；K(xi，xj)—核函数。

为了估计预算出样本点对应的在相机坐标系下的三维坐标，就需要求得SVM回归目标函数，即上面的式（9），最关键的在于C，ε，σ2三个参数的确定，这里采用k折交叉验证法与粒子群（PSO）算法结合的方式，进行参数寻优。

将一个样本点的图像坐标（u，v），绝对相位θ三个特征量作为一个输入向量，将所有数据分成训练集和测试集两部分，用训练集进行模型训练，得到的模型再用测试集来衡量模型的预测表现能力。以径向基函数为核函数，k折交叉验证误差作为SVM参数选择的目标值，在D维解空间内随机初始化随机粒子｛C，ε，σ2｝，这些粒子在D维解空间内以某种规律移动，经过若干次迭代后找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个是粒子本身的最优解Pid。另一个极值是整个粒子群目前找到的最优解Pgd。找到这两个极值后，每个粒子根据式（12）、式（13）更新自己的飞行速度和位置。

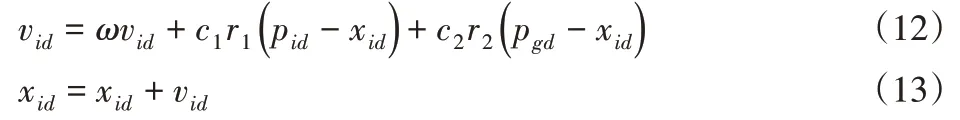
式中：i=1，2，…，m，m—粒子种群大小；d=1，2，…，D，D—空间维度为D维，即自变量的个数；ω—权重因子；c1，c2—学习因子，为非负常数；r1和r2是［0，1］之间的随机数［12］。

由以上步骤主要参考林智仁教授、李洋老师等编写好的SVM工具箱，对相关函数和MATLAB程序进行了适当的变形和改进，得到更精确的模型参数，使得SVM回归预测模型具有估计无偏性，可以有效避免过拟合，更稳定和精度更高。

4 实验验证与误差分析

实际应用中，对毛坯工件的定位精度要求达到0.3mm。根据上述理论方法，需要通过实验验证方法的精度是否符合工程需求。故进行以下实验的步骤。实验中用来标定的系统由巴斯勒相机、DLP投影仪、固定支架以及工作台等组成。调节视角使两者有公共视野，对着如下图5所示的圆点标定板进行图像采集。样本数据采集过程如下：（1）计算绝对相位。如下图5所示，对光栅图像应用八步法相移法，差分原理求解绝对相位。（2）单目相机标定。通过对标定板图像分析，得到相机内参和不同位置的外参。（3）对（1）（2）中得到的相位和坐标结果进行数据处理、存储。将同一标定点的相位值，图像坐标值，相机坐标系下三维坐标值对应起来，得到数据集（ui，vi，θ）i（xci，yci，zc）i。（4）在相机视野内，任意变换标定板的空间位姿。重复（1）（2）（3）三个步骤，得到尽可能覆盖整个测量空间的样本数据。因为每一个标定板上即可读取49个样本点，为了提高标定速度，同时保证标定精度，选用5个标定板上的样本点即可。

图5 标定数据集采集步骤Fig.5 Acquisition Procedures of Calibration Data Set

利用上述样本数据对上面的SVM回归预测模型进行训练，从而得到SVM标定模型。取得空间中的目标物表面的特征点50个，读取其相位值、图像坐标值，将其输入标定好的标定模型中，可得如下SVM回归模型预测结果显示。三个坐标轴的实际值（original）与回归预测值（predict）对比情况，如图6所示。

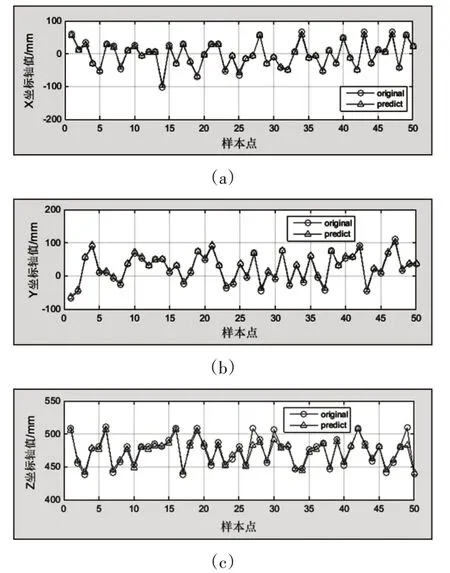
图6 三坐标轴实际值与回归预测值对比折线图Fig.6 Comparing the Actual Values of Three Coordinate Axes with the Predicted Values of Regression

三坐标值的回归预测计算值与实际的值对比，处理计算后可得三坐标轴值误差情况，如图7所示。

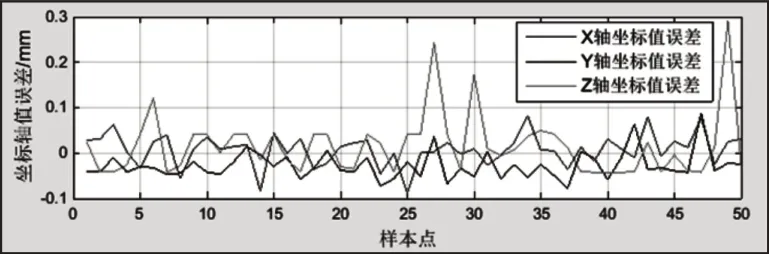
图7 三坐标轴回归预测误差值折线图Fig.7 Error Value of Three-Coordinate Axes Regression Prediction

分析数据时发现，回归预测数据与实际数据拟合情况良好。

回归预测误差的平均值AME为：

回归预测误差的最大值MAXE为：

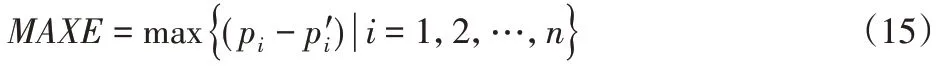
回归预测误差的均方误差MSE为：

平方相关系数r2为：

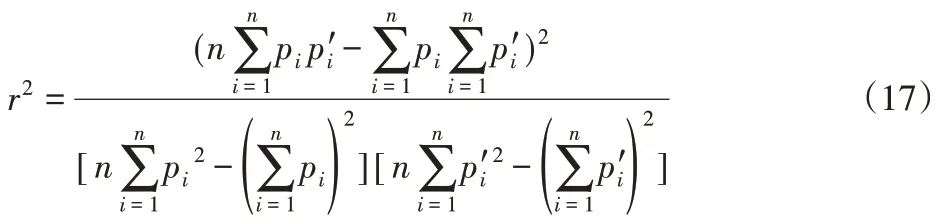
式中：pi、p′i—三个坐标轴回归预测值、真实值；n—样本个数。

空间任意一点预测坐标偏离实际坐标的距离d为：

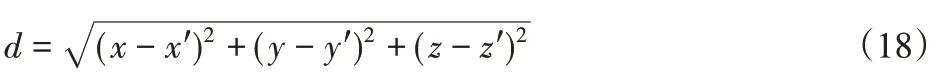
式中：x、y、z—预测值；x′、y′、z′—真实值。

三个坐标轴回归预测的误差值都取绝对值，将误差值的平均值、最大值、均方误差及平方相关系数都列出来，如表1所示。

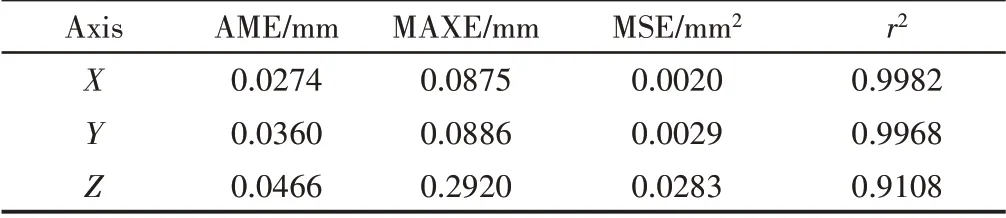
表1 三坐标轴值误差分析Tab1.Three-Coordinate Axis Error Analysis

由上表和式（16）、式（17）可得，三个轴的预测值的均方误差很小，相关系数都达到0.9以上，说明该标定模型较稳定。回归预测点位置与实际位置最大距离，即取三个坐标轴值误差代入公式，得到最大距离为0.32mm，而工程要求毛坯工件特征点空间定位精度需要达到0.3mm，并未达到要求精度。但是通过计算可得预测点与实际点平均距离为0.075mm，远远＜0.3mm，达到了工程需求。分析最大距离偏差较大的原因，可能是未对光栅图像进行进一步校正，引入了新的误差，下一步可对其进行深入分析。

5 结论

通过对上述视觉系统建立模型，并使用改进的粒子群算法，在MATLAB中，对采集到的数据集进行相位—三维坐标标定，并通过对比分析实验数据结果，可得以下结论：（1）应用SVM算法的相位—三维坐标标定方法是确实可行的，可以应用于实际工程，在光栅投影轮廓术进行三维重构的过程中进行精确的三维坐标的计算，对项目提供理论上的支持。（2）在误差允许范围内，以上应用SVM算法的相位—三位坐标标定模型精度工程要求。对实验数据进一步预处理后，定位精度可达到0.3mm。（3）以上单目相机与投影仪组合使用的视觉系统具有一定的稳定性，并可广泛适用于多种应用场景。