麦弗逊悬架主销轴线对半轴滑移的影响
2023-03-03李海亮涛LiHailiangFengBiChenTao
李海亮,冯 毕,陈 涛Li Hailiang,Feng Bi,Chen Tao
麦弗逊悬架主销轴线对半轴滑移的影响
李海亮,冯 毕,陈 涛
Li Hailiang,Feng Bi,Chen Tao
(北京汽车研究总院有限公司,北京 101300)
麦弗逊悬架由于结构紧凑、占据空间小,以及易于安装横置发动机,所以在轿车和轻型客车上应用广泛。利用MATLAB建立和求解某款车型的麦弗逊悬架运动学模型,通过调整摆臂外点位置改变主销轴线内倾角和后倾角,分析不同状态下悬架的跳动和转向对半轴移动节位移和摆角的影响,为后续悬架调整提供理论依据。
麦弗逊悬架;主销轴线;半轴滑移;MATLAB
0 引 言
麦弗逊悬架具有结构紧凑、占据空间小、成本低廉及维护方便等优点,在轿车和轻型客车上得到广泛应用。麦弗逊式独立悬架的运动学特性不仅影响汽车操纵稳定性、乘坐舒适性、行驶平顺性和轮胎使用寿命等方面,而且对半轴的滑移和摆角也有较大影响。
整车设计布置中,理论上半轴固定节的中心与主销轴线重合[1],但实际中由于各种原因,半轴固定节的中心与主销轴线有一定距离,本文在麦弗逊悬架模型上,引入半轴的运动模型,通过调整下摆臂外点的、坐标改变主销轴线,并分析对半轴位移和摆角的影响,为后续调整提供理论依据。
1 麦弗逊悬架模型
麦弗逊悬架结构如图1所示,提取硬点进行简化后如图2[2]所示。
为研究主销轴线对半轴滑移的影响,调整悬架点的、坐标,使半轴固定节节心点过悬架的主销轴线,调整后整备状态下各悬架硬点坐标如图3所示。
在软件CATIA中根据图3建立左悬架模型(左右悬架对称),并给出相应约束,完成DMU(Dynamic Model Update,动态模型更新),直线为主销轴线,设置跳动控制点为轮心点的坐标值,转向控制点为拉杆内点的坐标值。

图1 麦弗逊悬架结构

注:A为滑柱上点;B为滑柱下点;C为控制臂外点;D为控制臂前点;E为控制臂后点;F为转向拉杆外点;G为转向拉杆内点;H为轮心点;I为半轴固定节节心;J为半轴移动节节心;CK与DE垂直。

图3 悬架各硬点坐标值
通过悬架运动学结构特性[3-5],分析各个空间点的相对关系,利用MATLAB建立数学模型[2],计算出各硬点的空间坐标。
2 主销轴线变化对位移和摆角的影响
2.1 半轴固定节节心I在主销轴线上
图3中点在主销轴线上,根据MATLAB硬点坐标模型,进行转向和跳动模拟,得到半轴位移摆角曲线如图4所示。

图4 半轴位移摆角曲线(半轴节心通过主销轴线)
该状态的主销轴线内倾角为13.799°,主销后倾角为7.001°。图4中不转向跳动、左极限跳动、右极限跳动曲线基本重合,由此可知:当固定节节心与主销轴线重合时,转向对半轴的位移摆角曲线无明显影响。
2.2 控制臂外点C的X坐标前移
将图3中控制臂外点的坐标值正向移动5 mm和10 mm,得到半轴位移摆角曲线如图5所示。
当点的坐标值增加5 mm,主销后倾角减小0.404°;当点的坐标值增加10 mm,主销后倾角减小0.808°;二者的主销内倾角均没有变化。两种情况下,半轴固定节中心到主销轴线的距离分别为4.046 mm和8.098 mm。由图5可知:不转向跳动、左极限跳动和右极限跳动曲线随坐标值变化较明显,对于左悬架,车辆左转时半轴轴杆拉伸,车辆右转时半轴轴杆压缩;当坐标值变化5 mm时,左转极限和右转极限的半轴轴杆相比图4分别移动2.6、2.1 mm(图5(a)中坐标值增加5 mm后的左转极限滑移曲线距离左侧滑脱限制线16.33 mm,图4中原始左转极限滑移曲线距离左侧滑脱限制线18.94 mm,则坐标值变化后左转极限的半轴轴杆移动距离为18.94 mm-16.33 mm=2.61 mm;图5(a)中坐标值增加5 mm后的右转极限滑移曲线距离右侧滑脱限制线12.22 mm,图4中原始右转极限滑移曲线距离右侧滑脱限制线14.34 mm,则坐标值变化后右转极限的半轴轴杆移动距离为14.34 mm-12.22 mm=2.12 mm;以下各图计算方法相同,不再逐一列出),当坐标值变化10 mm时,左转极限和右转极限时的半轴轴杆相比图4分别移动5.4、4.3 mm,坐标值变化越大,则半轴轴杆位移越大,考虑整车发动机运动以及悬架衬套的影响,此时半轴出现滑脱或者与节壳顶死的风险较大。
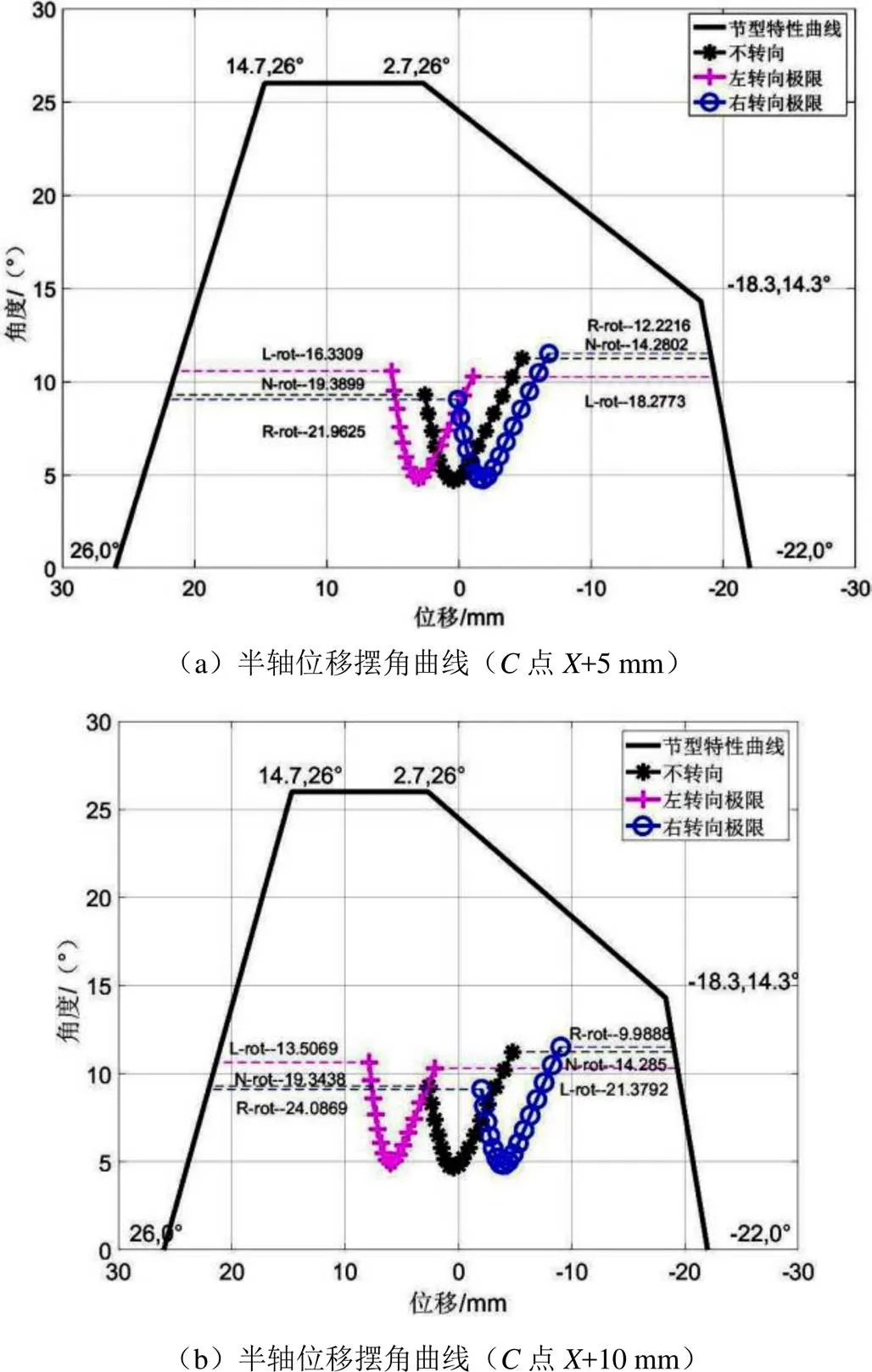
图5 半轴位移摆角曲线(C点X坐标值正向移动)
2.3 控制臂外点C的X坐标后移
将图3中控制臂外点的坐标值负向移动5 mm和10 mm,得到的半轴位移摆角曲线如图6所示。

图6 半轴位移摆角曲线(C点X坐标值负向移动)
当点的坐标值减小5 mm,主销后倾角增加0.403°;当点的坐标值减小10 mm,主销后倾角增加0.805°;二者的主销内倾角均没有变化。两种情况下,半轴固定节中心到主销轴线的距离分别为4.039 mm和8.072 mm,与图5类似,不转向跳动、左极限跳动和右极限跳动曲线随坐标值变化较明显,但与图5变化方向相反,对于左悬架,车辆左转时半轴轴杆压缩,车辆右转时半轴轴杆拉伸;当坐标值变化5 mm时,左转极限和右转极限的半轴轴杆相比图4分别移动2.4、2.0 mm,当坐标值变化10 mm时,左转极限和右转极限的半轴轴杆相比图4分别移动4.7、3.9 mm,坐标值变化越大,则半轴轴杆位移越大,考虑整车发动机运动以及悬架衬套的影响,此时半轴出现滑脱或者与节壳顶死的风险较大。
2.4 控制臂外点C的Y坐标内移
将图3中控制臂外点的坐标值正向移动5 mm和10 mm,得到半轴位移摆角曲线如图7所示。
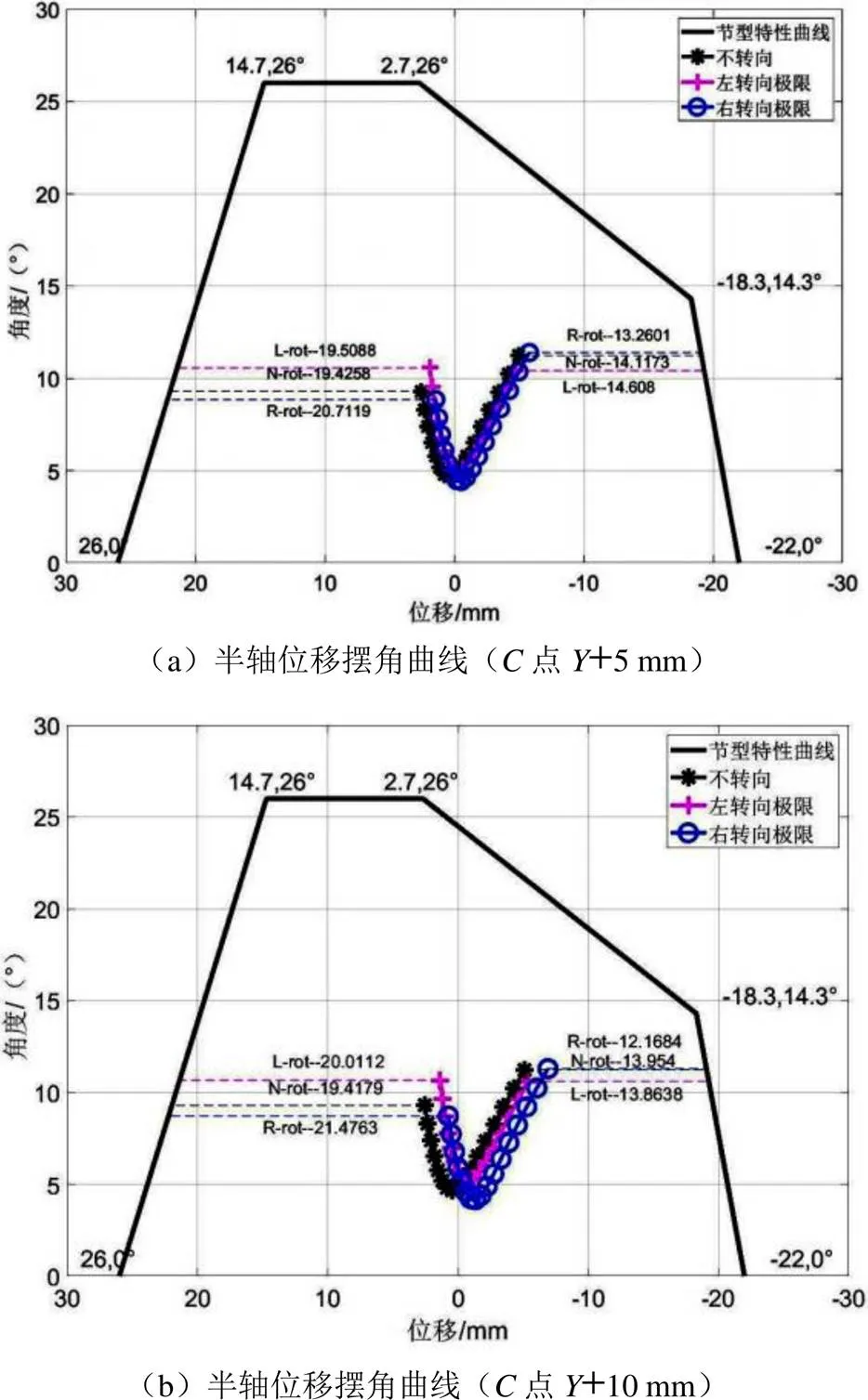
图7 半轴位移摆角曲线(C点Y坐标值正向移动)
当点坐标增加5 mm,主销内倾角减小0.387°;当点坐标增加10 mm,主销内倾角减小0.774°;二者的主销后倾角均没有变化。两种情况下,半轴固定节中心到主销轴线的距离分别为3.963 mm和7.937 mm。由图7可知:不转向跳动、左极限跳动和右极限跳动曲线随坐标值变化的幅度小于随坐标值变化的幅度;对于左悬架,车辆左转或右转半轴轴杆均压缩;当坐标值变化5 mm时,左转极限和右转极限的半轴轴杆相比图4分别移动0.5、1.1 mm,当坐标值变化10 mm时,左转极限和右转极限的半轴轴杆相比图4分别移动1.1、2.2 mm,坐标值变化越大,则半轴轴杆位移越大。
2.5 控制臂外点C的Y坐标外移
将图3中控制臂外点的坐标值负向移动5 mm和10 mm,得到半轴位移摆角曲线如图8所示。

当点坐标值减小5 mm,主销内倾角增大0.385°;当点坐标值减小10 mm,主销内倾角增大0.769°;二者的主销后倾角均没有变化。两种情况下,半轴固定节中心到主销轴线的距离分别为3.948 mm和7.884 mm,与图7类似,但变化方向相反,对于左悬架,车辆左转或右转半轴轴杆均拉伸;坐标值变化越大,则半轴轴杆位移越大,与图7中坐标值正向移动时的变化范围基本相同。
综上,得到主销轴线变化对半轴位移和摆角的影响,结果见表1。
由表1可知:(1)控制臂外点坐标值变化只影响主销后倾角变化,坐标值变化只影响主销内倾角变化,但前者对转向极限的半轴轴杆的位移影响更大,且前者的左右转向极限曲线位于不转向曲线两侧,而后者位于不转向曲线同侧;(2)随着控制臂外点坐标值变化幅度增大,主销后倾角变化幅度也增大,转向极限的半轴轴杆位移变化也增大,半轴轴杆与移动节壳间干涉或滑脱的风险也增加;随着控制臂外点坐标值变化幅度增大,主销内倾角变化幅度也增大,转向极限的半轴轴杆位移变化也增大,半轴轴杆与移动节壳间干涉或滑脱的风险也增加;(3)随着控制臂外点、坐标值由正向向负向变化,左右转向极限曲线在不转向曲线两侧的分布也发生了方向对换。

表1 主销轴线对半轴位移和摆角的影响
3 结束语
本文分析了麦弗逊悬架主销轴线的变化对半轴位移和摆角的影响,为后续车型开发中滑移曲线的优化方向提供参考,提高了开发效率。
[1]王霄锋. 汽车底盘设计[M]. 北京:清华大学出版社,2010.
[2]李海亮.麦弗逊悬架车辆半轴位移摆角图的Matlab实现[J].北京汽车,2022(2) :32-35.
[3]凌晨,韩权武,刘春梅,等.麦弗逊式悬架运动分析[J].汽车工程学报,2015,5(6):448-453.
[4]耿庆松,秦伟,黄勇刚,等.麦弗逊独立悬架空间运动学分析[J].机械设计与制造,2015(1):20-23.
[5]李晏,张姗,王威,等.麦弗逊悬架运动分析的空间解析法及MATLAB实现[J].中国工程机械学报,2015,13(1):16-21.
2022-10-11
1002-4581(2023)01-0001-05
U463.330.2
A
10.14175/j.issn.1002-4581.2023.01.001
