仿人机器人手臂动作模仿系统的研究与实现

刘世平，胡 竹，程 力，付 艳

（华中科技大学机械科学与工程学院，湖北 武汉 430074）

1 引言

随着微软Kinect体感设备的推出，国内外研究机构和科研人纷纷以此作为平台进行研究和开发，现已经将其应用于机器人［1-3］、医疗［4-5］、教育［6-7］、动画［8-9］、电子商务［10］和计算机［11］等领域。在研究人类智能的平台中，仿人机器人有着独特的地位，是一个多学科融合的复杂智能系统。经过半个世纪的发展，仿人机器人技术在机器人领域占有越来越重要的地位［12］。

随着Kinect技术的进一步成熟和充分挖掘，Kinect与仿人机器人结合开发的潜力受到越来越多的研究者关注，同时为人机交互带来了质的突破［13］。作为机器人学最重要的研究方向之一，人机交互最直观的实现方式就是模仿。机器人动作模仿系统的研究已取得了一定进展，华南理工大学的陈家顺利用动作交互技术实现了Nao机器人的动作模仿，但由于人体关节结构与Nao机器人关节结构存在差异性，通过动作交互的方式实现机器人动作模仿并不能达到示范者期望姿态［14］。重庆邮电大学的林海波教授等人利用Kinect的骨骼追踪技术计算了人体腰、肩、肘和腕四个关节的转动角度，将这四个角度与四自由度机械臂的四个关节一一对应，实现体感交互［15］，但其实现的是动作匹配而不是动作模仿。

这里首先建立起机器人系统，将系统各部分功能与设备进行介绍。不同于其他研究者使用产品化的仿人机器人，这里所做研究基于一款完全自主制造的仿人机器人。利用Kinect体感摄像机获取人体骨骼数据，并将其进行霍尔特指数平滑滤波处理后用于坐标转换。通过对机器人手臂重要关节的建模，实现将人体骨骼数据转换为机器人手臂相应伺服电机的转动角度。成功实现仿人机器人手臂动作模仿。这里所述建模方法，只需利用人体三个关节的三维坐标便可控制四个伺服电机的转动，数据处理的工作量小。实验结果表明，利用这里提出的建模方法进行坐标变换能够实现仿人机器人的动作模仿，并且效果良好，实时性较强。

2 机器人系统的构建

这里研究以四自由度仿人双臂机器人为对象，机器人系统包括信号采集系统、上位机、下位机、机械运动系统四个部分，如图1所示。

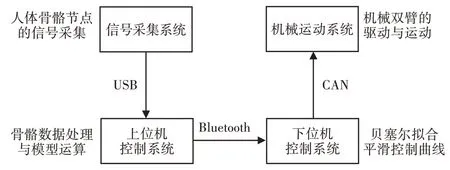
图1 机器人系统框图Fig.1 Robot System Block Diagram

2.1 信号采集系统

信号采集系统使用Kinect体感摄像头［16］。使用时，Kinect将安置在人的前方，采集人体骨骼节点信号，用于后续的数学建模中。Kinect安置高度没有固定标准，根据使用经验，使其略带俯视人体的初始高度与角度效果较好，这样的高度可以使获得的骨骼节点信号更加稳定。信号采集系统通过USB与上位机控制系统相连接，将采集到的人体骨骼节点信号传输到上位机控制系统。

2.2 上位机控制系统

上位机是一台普通PC，它将接收到的人体骨骼节点信号进行滤波处理，同时利用骨骼节点信号建立相应的数学模型，根据所建立的数学模型计算得出机器人手臂各关节的控制信息。上位机控制系统通过Bluetooth与下位机控制系统进行无线通信，将控制信息发送给下位机控制系统。

2.3 下位机控制系统

下位机使用的是STM32主控板。下位机控制系统接收到上位机控制系统发送过来的控制信息后，利用贝塞尔曲线对控制信息进行平滑处理。将平滑处理后的控制信息通过CAN总线发送到机械运动系统［17-18］，驱动机器人手臂各关节的电机运动。

2.4 机械运动系统

机械运动系统包含机械双臂与伺服电机及其控制器。这里所使用机械臂是一款完全自主设计的四自由度机械双臂，每个机械臂拥有四个自由度，包含两个在肩部的自由度，两个在肘部的自由度。机械臂正视图与自由度分布简图，如图2所示。手臂使用的电机为瑞士MAXON的RE系列伺服电机，控制器为MLDS3065C。

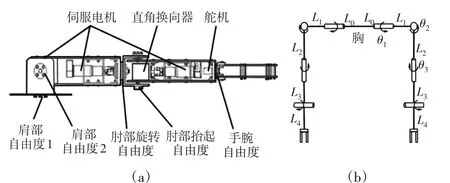
图2 机械臂正视图与自由度分布图Fig.2 Front View of Robotic Arm and Degree of Freedom Distribution Diagram

3 机器人手臂运动建模

在仿人机器人手臂动作模仿模型中，主要考虑肩部与肘部关节的运动。下面以左臂为例分别介绍机器人肩部与肘部的建模方法与思想。

3.1 机器人肩部关节建模

为便于电机的控制，这里采用发送角度数据的方式来控制仿人机器人手臂的运动。本模型重点在于将人手臂运动时肩部关节的一个角度，分解为仿人机器人肩关节的两个伺服电机所需要的旋转角度，并得到相应的数学关系。

这里在Kinect上建立了绝对坐标系，在操作者的肩部建立了相对坐标系。绝对坐标是指：人手臂骨骼点在Kinect CameraSpacePoint坐标系（以深度摄像头为原点）中的坐标，如图3所示。

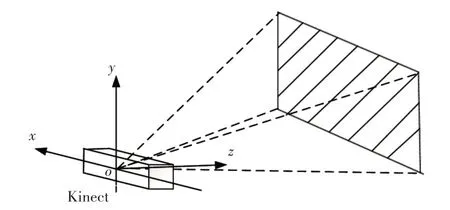
图3 Kinect绝对坐标系Fig.3 The Absolute Coordinate System of Kinect

相对坐标是指坐标系原点建立在操作者肩部的坐标系，如图4所示。图中：O点—左肩关节（SHOULDER_LEFT）；P点—左臂肘部关节（ELBOW_LEFT）；Q点—沿Y轴负方向，与O点距离为k的确定点（实际上最终结果与k毫无关系，这里只是为了便于表述）。建立相对坐标系是为了便于将操作者手臂的动作分解为适合机器人手臂各关节的运动量。

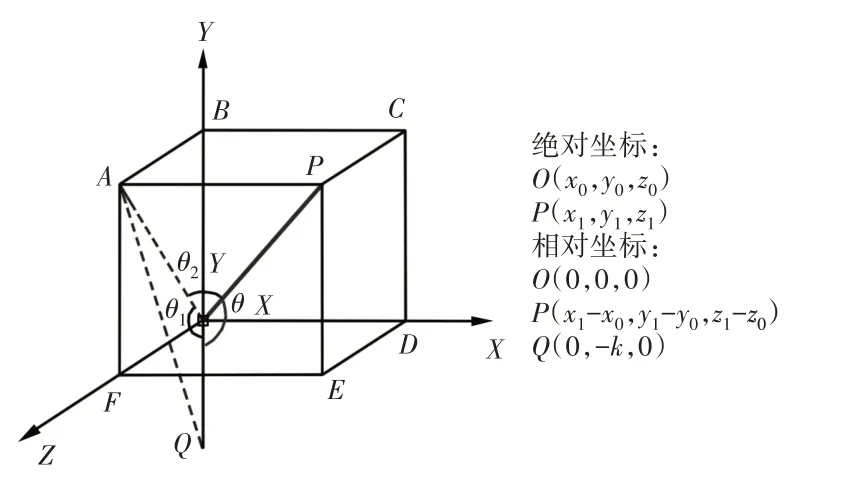
图4 相对坐标系Fig.4 The Relative Coordinate System

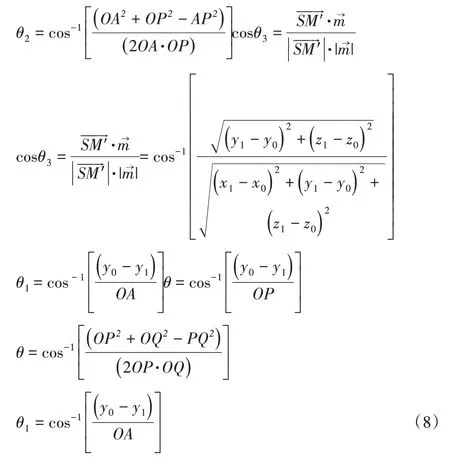
已知：OQ=k，通过Kinect可获得在绝对坐标系中各点的坐标分别为：O（x0，y0，z0），P（x1，y1，z1），Q（x0，y0-k，z0），则在相对坐标系中各点的坐标分别为O（0，0，0），P（x1-x0，y1-y0，z1-z0），Q（0，-k，0），令∠POQ=θ，∠AOQ=θ1，∠AOP=θ2；相对坐标系中取A（0，y1-y0，z1-z0），C（x1-x0，y1-y0，0）；

在△POQ中，

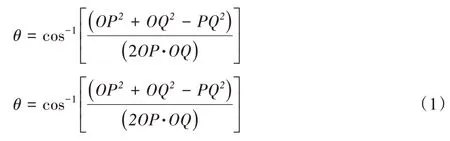
在△AOQ中，

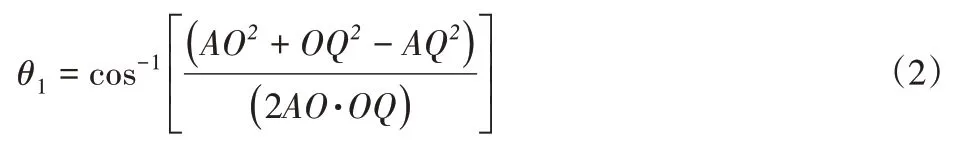
在△AOP中，

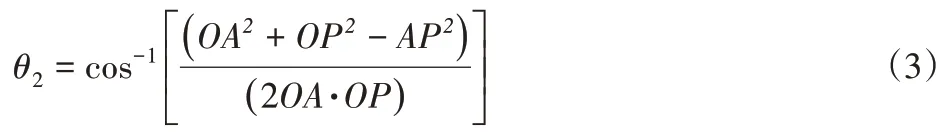
则：

式中：θ—人手臂运动时的角度；

θ1、θ2—电机所需的控制角度。

因此可以根据Kinect获取的绝对坐标来计算出相应的角度。分别控制肩部两个电机转动θ1、θ2来实现机械臂的运动，达到模仿人手臂动作的目的。

3.2 机器人肘部关节建模

肘部关节同样有两个自由度，假定θ1、θ2、θ3、θ4均不为0（θ1、θ2、θ3、θ4分别对应机械臂上的四个电机转动角度，从上到下依次编号）。

在肩部关节建立坐标系，如图5所示。图中：O′、P、M—人的左肩、肘部、手腕三个骨骼点，则：O′P与Y′轴负方向夹角为θ；O′P在Y′O′Z′面上投影与Y′轴负方向夹角为θ1；O′P与其在Y′O′Z′面的投影间的夹角为θ2。

图5 肩部关节角度变换Fig.5 The Shoulder Joint Angle Change

按图5箭头所示方向从左向右看，可得肘部关节坐标系，如图6所示。

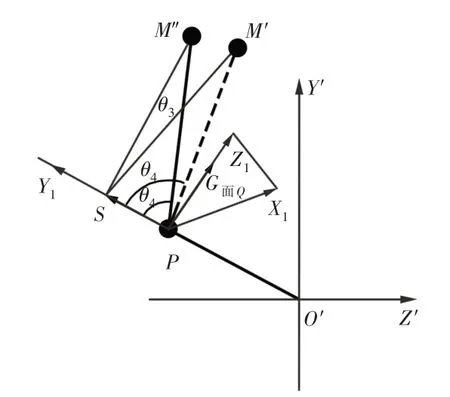
图6 手臂运动时肘部关节坐标系Fig.6 The Elbow Joint Coordinate System when the Arm Movement

图中：M′—手腕实际位置（此时θ3≠0）；M″—人为假设的手腕位置（此时θ3=0）；当手腕在M′′位置时，肘部关节点的坐标系为PX1Y1Z1。设初始状态时（即θ1、θ2、θ3、θ4均为0），肘部关节点的坐标系为P′X1′Y1′Z1′，如图7所示。

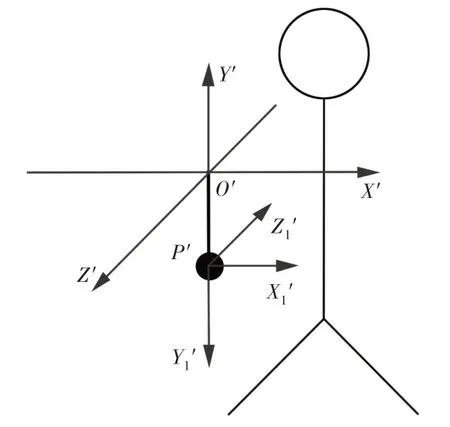
图7 手臂自然放下时肘部坐标系Fig.7 The Elbow Coordinate System when the Arm Natural Decline

对于图6，通过Kinect可得到O′、P、M′三点的绝对坐标，进而得到这三点在坐标系O′X′Y′Z′中的相对坐标，如下所示：

通过O′、P、M′三点坐标构造向量，由这两向量可以计算出θ4角度。

根据Kinect关节点坐标系的定义，Y1轴始终由父节点指向子节点（即由肩部关节点指向肘部关节点），所以Y1轴沿O′P；由于θ4θ4确定，故无论θ3为多少，PM′、PM′′与O′P延长线夹角都不改变，均为θ4，即肘部与手腕所在直线以Y1轴为旋转中心旋转，则，由O′P可得Y1轴的单位向量，故=(PM′*由此推得S点坐标，进而得到，若设面Ω垂直于直线O′P且经过P点，显然平行于面Ω。

需要注意的是，当手臂运动时，肩部坐标系是固定不变的，而肘部坐标系将随着手臂的运动而改变坐标系自身的状态。人手大臂（OP）运动时，肘部坐标系（PX1Y1Z1）发生旋转后的状态，如图8 所示。图中：Z1′′轴—Z1轴从肘部关节点平移到肩部关节点的表示。

图8 手臂运动时肩部坐标系旋转示意图Fig.8 The Shoulder Coordinate Rotation Schematic Diagram when the Arm Movement

在图8中，肩部关节的角度θ1会影响到Z1轴的方向，沿Z1′′轴方向向量由图8知的方向即为当手腕到达M′′位置时肘部关节点的Z1轴方向。

当θ3=0时，手腕在面Ω的投影在Z1轴上，为，可以用替代。由于第三个电机的轴在O′P上，所以θ3可在面Ω上进行计算得到：

4 实验设计与分析

4.1 实验任务

为了验证上文建立的机器人手臂运动模型，直接采用人机交互的方式进行实验。示教者站在原地连续挥动自己的手臂，Kinect实时采集所需关节（肩部、肘部、腕部）的数据。按照上述建模方法进行运算，得到电机转动的角度。通过上位机控制系统将角度信息发送至下位机控制系统，从而驱动伺服电机实现手臂动作模仿。

4.2 实验数据处理

实验过程中，出现了机器人手臂动作会有抖动的现象。这是因为人肢体形状复杂以及外界环境干扰导致Kinect直接采集的人体骨骼节点信号干扰多，数据处理复杂导致的。以肘部数据为例进行分析（肩部和腕部方法相同）。取肘部的3组原始数据，每组包含100个数据点，如图9所示。（横坐标表示数据点，纵坐标表示数据点对应的坐标值。）

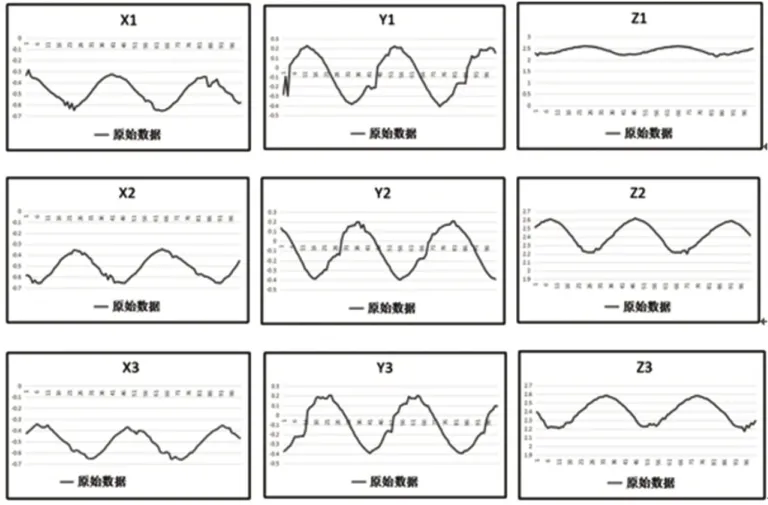
图9 肘部关节的空间三维坐标原始数据图Fig.9 Spatial Three-Dimensional Coordinates Original Data Figure of the Elbow Joint

由图9可知，肘部关节原始数据存在着明显的波动，因示教者站在原地挥动手臂，Z坐标变化幅度较大。为了获得更加平滑的数据，这里采用霍尔特指数平滑法［19］对原始数据进行滤波处理。通过滤波处理后的数据，如图10所示。

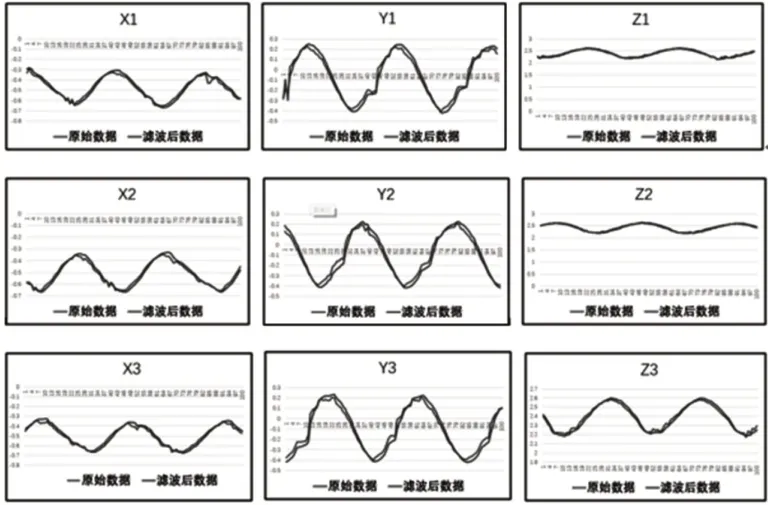
图10 滤波处理后数据与原始数据对比图Fig.10 After Filtering Processing Data Compared with the Original Data

图10中，肘部的X、Y、Z坐标经滤波处理后，得到的曲线相比于原始数据更加平滑。原始数据中的波动得到很好的处理，稳定性加强。

4.3 实验效果与分析

将滤波后得到的平滑数据用于计算相应伺服电机的旋转角度，控制相应电机。实验结果表明，这里所述建模方法能够达到使用要求，构建的基于Kinect 的仿人机器人手臂动作模仿系统可以实现实时连续动作模仿。实时动作模仿效果，如图11所示。

图11 实时动作模仿效果图Fig.11 Real-Time Imitation Rendering

5 结论

这里建立了仿人机器人系统，将系统各部分功能与设备进行介绍。利用Kinect体感摄像机的骨骼追踪技术，采集示教者的重要关节骨骼点三维空间坐标，利用霍尔特指数平滑滤波处理骨骼数据，有效解决了原始数据出现的波动现象，使数据更加平滑。基于骨骼数据建立仿人机器人手臂重要关节的数学模型。利用模型将人体骨骼数据转换为机器人手臂相应伺服电机的控制信息。通过主控计算机发送到机器人主控制器驱动各关节伺服电机转动。成功实现仿人机器人手臂动作模仿。这里所述建模方法，只需利用人体三个关节的三维坐标便可控制四个伺服电机的转动，每一个关节的角度求解都是通过简单的向量运算与三角运算实现，模型计算简单，因而可以使动作模仿的实时性较好。此外，利用人体骨骼数据来建立相应模型，能够让动作模仿的更加准确。实验结果表明，这里所述建模方法适用于仿人机器人手臂动作模仿系统，能够实现实时动作模仿，且运动平滑无抖动，动作模仿效果较好。