基于Bayes网络高性能滚动轴承失效影响因素可靠性评估方法

韩 兴，李 昌，陈正威，李云飞

（1.辽宁科技大学机械工程与自动化学院，辽宁 鞍山 114051；2.中国能建东电一公司，辽宁 沈阳 110179）

1 引言

滚动轴承是重大装备的关键基础零部件，尤其是对于精密机床、高速列车、航空发动机等重大核心装备，高性能滚动轴承的自主设计与制造，直接体现了一个国家高端制造的能力和水平。我国作为制造业大国，轴承产量居于世界前列，但以中低端轴承生产制造为主，对于高端轴承制造技术的掌握上还远远不够，高性能轴承仍大量依赖进口［1］。从滚动轴承使役全寿命周期来看，影响轴承使役性能的影响因素较多，开展对轴承失效机理的各种影响因素可靠性定量评估具有重要意义，可为高端轴承的控型控性制造以及延寿设计提供理论依据。

目前，对滚动轴承失效分析主要是基于轴承运行信号的测量，运用专家经验知识主观诊断［2］。因轴承结构、使役过程及使役环境动态变化的复杂性，轴承的失效故障征兆与引起故障的原因之间呈现一对多或多对一的复杂耦合性，不是简单的一一映射，轴承失效分析出现许多随机因素，导致失效分析过程产生大量现有方法难以解决的随机性问题。当使役轴承出现失效时，现有的故障树分析、可靠性框图等方法很难给出是哪种失效影响因素对轴承故障失效的条件贡献概率，而条件贡献概率对于准确了解滚动轴承的使役损伤机理具有重要的实践意义。

从20世纪60年代开始，国内外对轴承失效诊断进行了大量研究，采用如频谱分析法、冲击脉冲法、共振解调法、计算机分析软件以及人工智能与计算机技术相结合方法，但对失效影响因素定量评估的研究相对较少。导致轴承寿命降低的因素既有制造、材料缺陷，还有使用不当、维护和润滑不良等原因，贯穿轴承设计、制造、使役全周期。准确分析各种失效原因并对其发生概率进行定量评估，进而提出有效的预防措施，必将延长滚动轴承的寿命［3-4］。这里在对滚动轴承常见的失效特征、机理、影响因素系统分析基础上，总结了失效影响因素随机性来源，建立了高性能滚动轴承失效影响因素故障树模型，直接映射建立其Bayes网络模型，利用桶排除法对轴承失效概率及中间失效结点概率进行了计算，利用全概率公式对轴承失效过程各影响因素的条件概率进行了可靠性定量评估。

2 基于Bayes网络可靠性评估原理

Bayes网络又称为Bayes信念网络，是随机性知识表达和推理领域最有效的理论模型之一。1988年Pearl提出Bayes网络定义，几十年来一直是研究的热点。1763年所提出的贝叶斯理论是其重要理论基础。Bayes网络是一种带有条件概率的有向无环图DAG（Directed Acyclic Graph），它由代表变量的结点及连接这些结点的有向弧构成，其结点表示随机变量，结点弧反映了随机变量间的条件依赖关系，即相关影响概率。Bayes网络是基于概率分析和图论的一种定性知识表达和推理模型。直观来看，Bayes网络表现为一个赋值的复杂因果关系网络图，网络中的每一个结点表示一个变量（随机事件），各个变量之间的弧表示事件发生的直接因果关系。其网络结构反馈出对事件之间因果联系的定性表达，边缘概率和条件概率表明了原因对结果的定量影响程度。Bayes网络的计算推理过程实质上是基于Bayes概率理论的概率计算过程。Bayes网络依据随机变量间条件独立性，将一个联合概率分布直观的表达为一个图形网络结构，进而推导出一系列的条件概率表，经过变量消元计算出任意变量和部分变量的概率分布，在证据变量取值已知的情况下，可计算关心结点变量的条件概率分布［5］。

由Bayes公式可得出条件概率公式为：

式中：W—随机事件；B—条件事件；P—概率。

假设W变量存在n个状态情形，分别为（w1，w2，…，wi，…，wn），则由全概率公式可以计算得出：

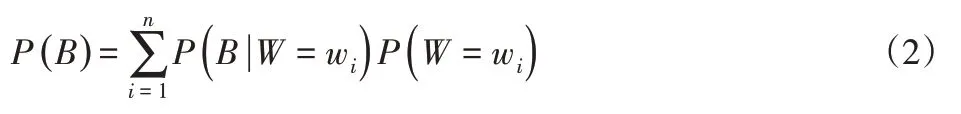
根据Bayes公式计算出后验概率P（W|B）。Bayes网络既可正向推理，从先验概率（原因）得出后验概率（结果），反之也可由结果推导原因，计算常用精确推理计算方法中的桶排除法。

3 高性能滚动轴承失效影响因素可靠性评估

3.1 滚动轴承失效影响因素Bayes网络的建立

从滚动轴承使役全周期来看，影响轴承使役寿命的主要因素可分为人为因素、事物因素、环境因素和管理因素。因此，对轴承失效因素分析应该从这四个方面入手，如图1所示。人为因素主要包括制造过程中的误差、材料选取的不合理导致材料缺陷以及安装使用过程中操作规范性不符合要求，甚至违规操作等。事物因素主要发生在使役过程中，轴承使役时间达到了设计的疲劳寿命极限而失效。

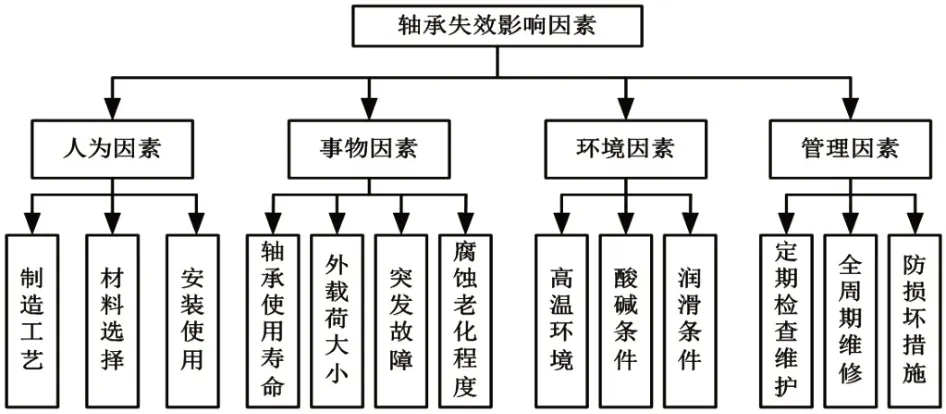
图1 轴承失效影响因素Fig.1 Bearing Failure Factors

轴承工作的外载荷对其失效产生重要影响，过大的外载荷会加速轴承的失效。轴承的腐蚀老化也会对轴承寿命产生影响，造成失效。环境因素主要是指轴承的工作环境对轴承寿命产生的影响，主要包括高温、高压、强酸、强碱、混合电磁场和粉尘颗粒较大的环境。管理因素主要包括定期检查维护和采取防损坏措施。滚动轴承的主要失效形式分为止动失效和精度丧失两种。止动失效是指轴承因失去工作能力而停止转动，例如：卡死、断裂等现象。精度丧失是指因轴承尺寸变化而致使其失去原设计精度，此时，轴承未失去转动能力，但属于非正常转动，例如：磨损、腐蚀［6-8］。对于航空发动机主轴上的滚动轴承来说主要失效形式有滚道表面烧伤、磨损，滚动体打滑，滚道表面疲劳剥落及保持架变形破裂。根据滚动轴承的失效形式和特征，可将其损伤机理分为：接触疲劳失效，摩擦磨损失效、断裂失效、变形失效、腐蚀失效和游隙变化失效等形式［9-11］。根据轴承失效形式，将轴承失效作为顶事件，将各种失效形式作为中间事件，再追究引起各类失效的根本原因，找到基本事件，通过联系上层事件，逐层剖析，得到基本事件与上层事件的逻辑关系，建立条理清晰的故障树，故障树模型［12-18］如图2所示。滚动轴承失效故障树事件，如表2所示。假设故障树的底事件间相互独立，并且底事件均只存在两种状态：失效发生和不发生。设定轴承失效基本底事件服从威布尔分布。

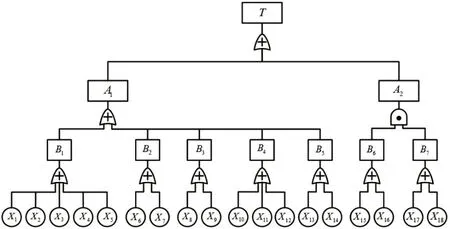
图2 轴承失效故障树Fig.2 Bearing Failure Fault Tree

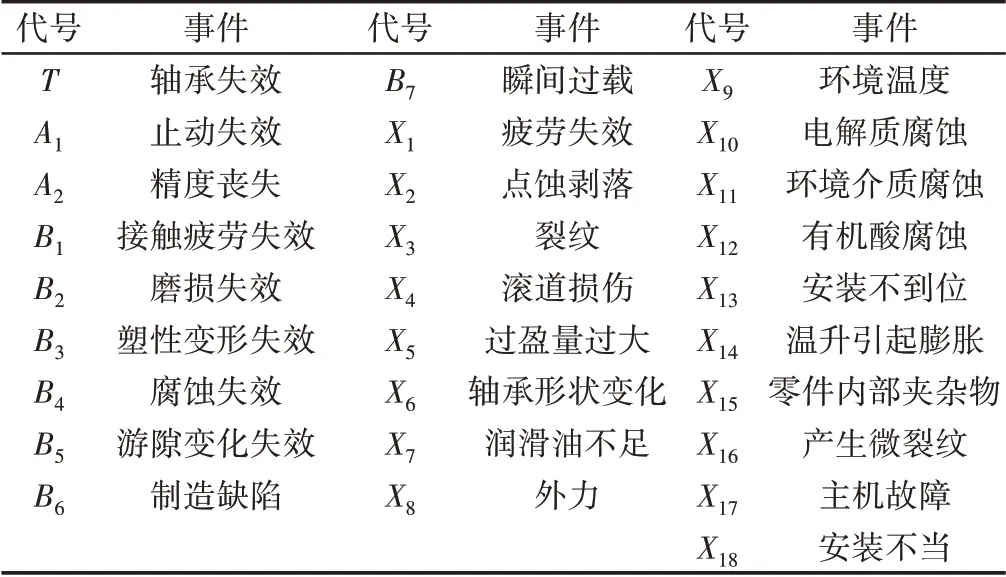
表2 轴承失效故障树事件Tab.2 Events of the Bearing Failure Fault Tree

令位置参数α=0，则为二参数威布尔分布。

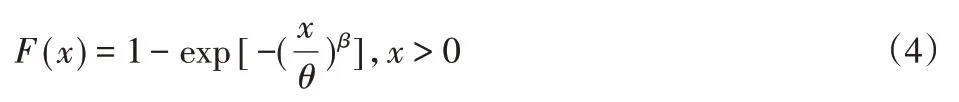
当形状参数β=1时，威布尔退化为指数分布。

假设轴承工作时间为每天24小时每年360天，将基本事件故障率带入式（5），得到底事件的失效率和失效概率为后续概率计算参数，如表3所示。根据所建立的故障树直接映射建立Bayes网络，将故障树中每个事件、逻辑门均转化为Bayes网络里相应的结点，如图3所示。

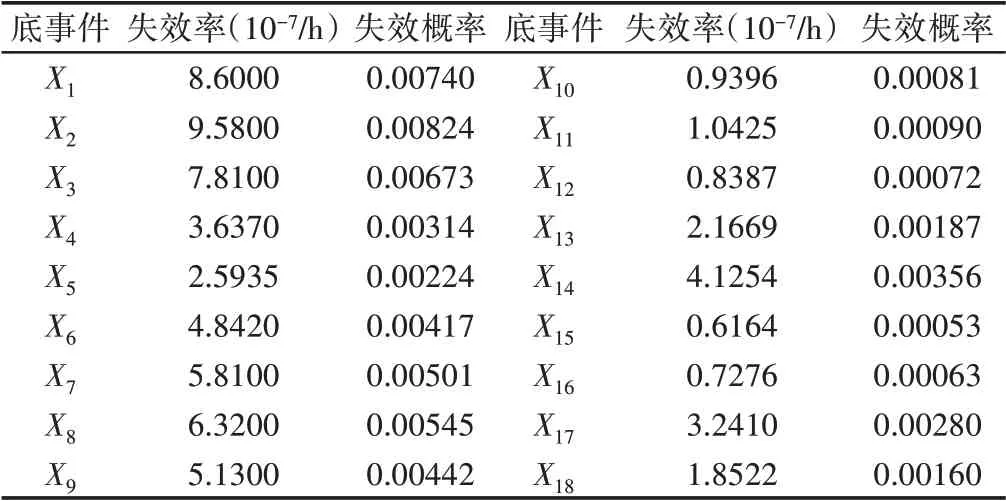
表3 计算参数Tab.3 Calculation Parameters

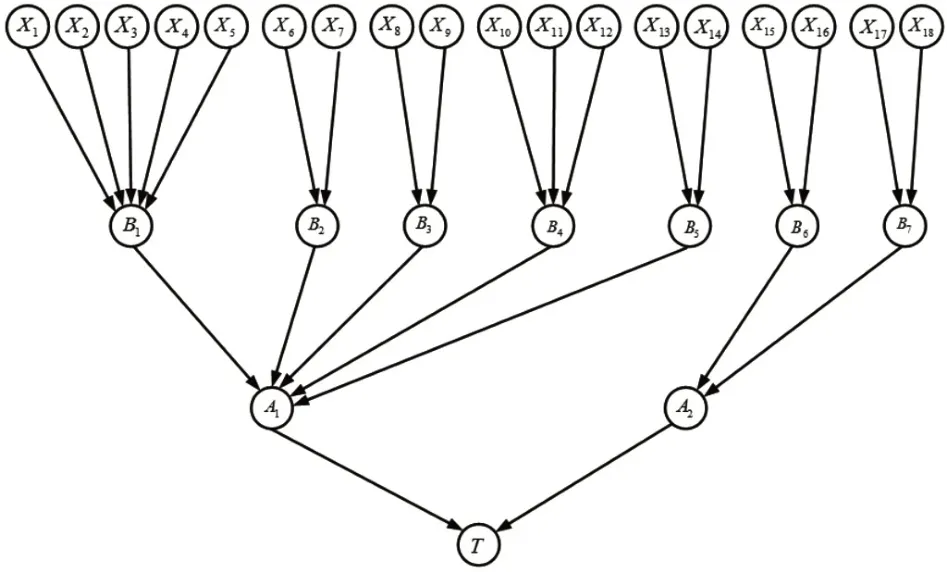
图3 轴承失效Bayes网络Fig.3 Bayes Network of Bearing Failure

3.2 利用桶排除法计算轴承失效概率及中间失效结点概率

桶排除法是一种基于组合优化的精确推理算法，A1为或门结点，A2为与门结点，B1～B7均为或门结点，利用如下桶排除计算轴承失效概率及中间失效结点概率，进而根据图3所建立的轴承失效Bayes网络进行因果推理［19］，可获得各底事件失效发生条件下，系统各个失效结点及顶事件失效的概率，如表4所示。

表4 各底事件失效时系统结点失效概率Tab4 The Failure Probabilities of the System Nodesat the Time of Failure of Each Basic Event

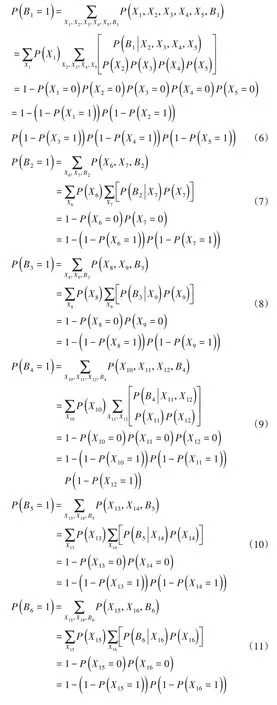
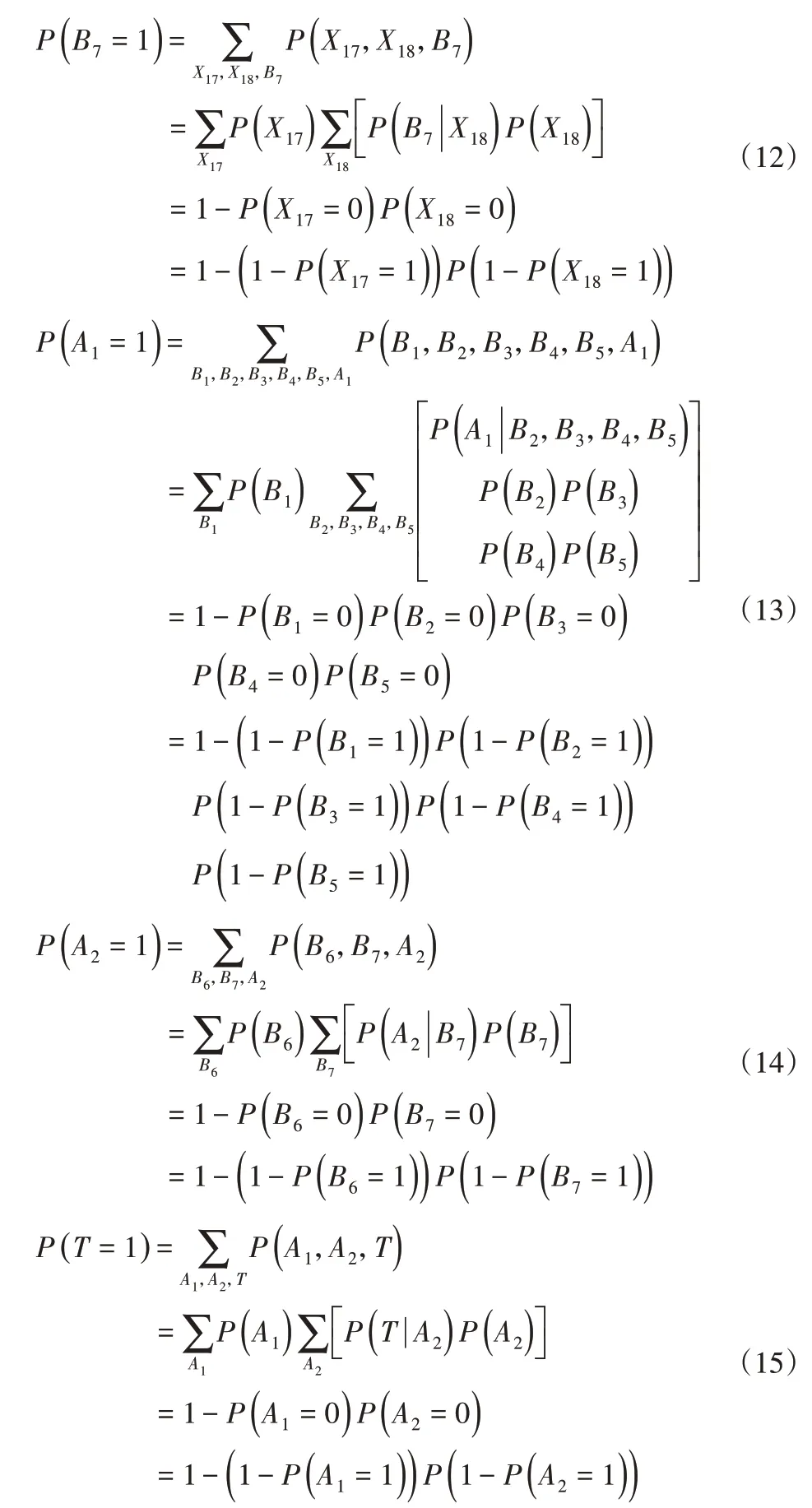
3.3 轴承失效时各失效影响因素可靠性评估

进行诊断推理过程中，假定轴承失效T发生时，由条件概率公式（1）可分别计算得出每一个底事件对于轴承失效的贡献概率值结果，如表5、图4所示。计算表明：接触点蚀剥落对轴承失效贡献概率最大，为15.454%，轴承零件内部夹杂物失效的条件概率为0.058%，影响最小。X1疲劳失效和X2剥落失效对轴承失效的影响相对较大，而X15轴承零件内部夹杂物失效、X16轴承零件内部产生微裂纹失效贡献概率相对较小。

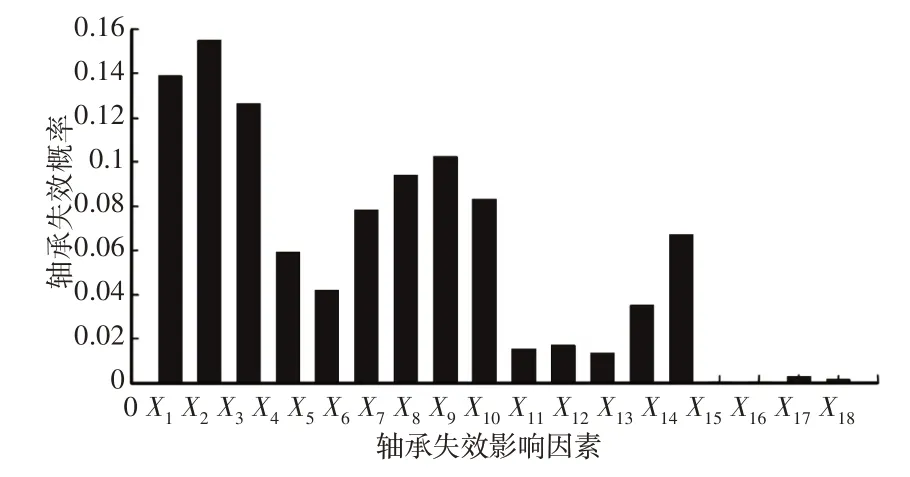
图4 轴承失效时各影响因素贡献概率柱状图Fig.4 The Histogram of the Contribution Probability of Each Influence Factor of the Bearing Failure

表5 轴承失效时各影响因素的贡献概率Tab.5 The Contribution Probability of Each Influence Factor of the Bearing Failure

为了能更好的表明各个失效影响因素对轴承失效影响概率，分别将X1、X2对T影响关系，X15、X16对T影响关系进行统计计算结果，如图5、图6所示。计算表明：X1、X2对T影响关系，如图7、图8所示。计算表明：两种失效因素对B1和A1均产生明显影响，但影响趋势相近。计算得出的各种失效影响因素对轴承失效的影响曲线，如图9所示。计算表明与门交集影响因素X15～X18影响曲线相近，对轴承失效的贡献概率较小，而或门并集影响因素X1～X14影响曲线相近，对轴承失效的贡献概率较大，轴承失效概率随着这些影响因素概率的增加明显增大。

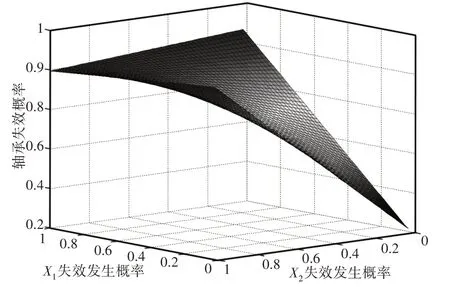
图5 X1、X2失效发生对轴承失效T的影响Fig.5 The Influence of the Failure of X1 and X2 on the Bearing Failure T

图6 X15、X16失效发生对轴承失效T的影响Fig.6 The Influence of the Failure of X15 and X16 on the Bearing Failure T

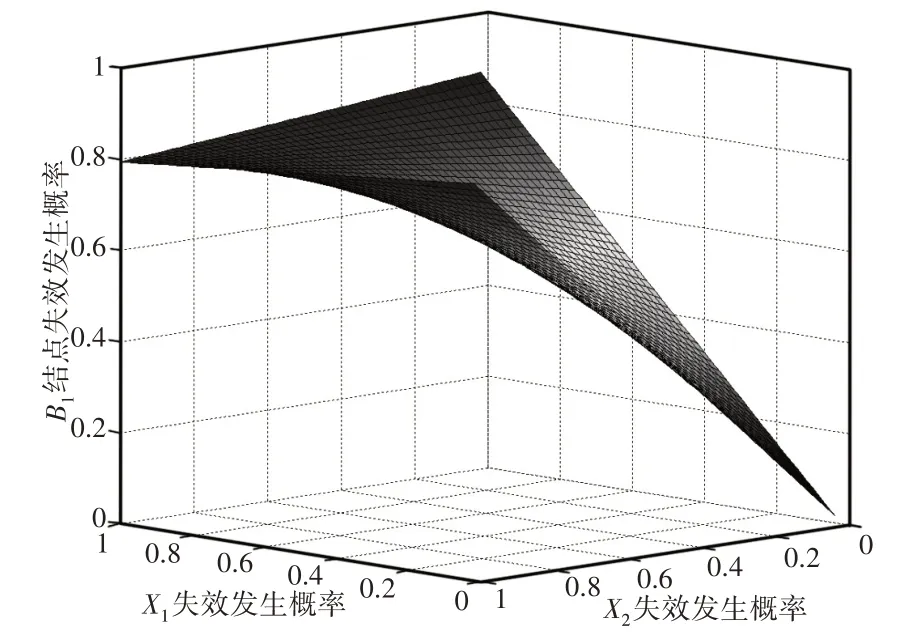
图7 X1、X2失效发生对失效结点B1的影响Fig.7 The Influence of the Failure of X1 and X2 on the Failure

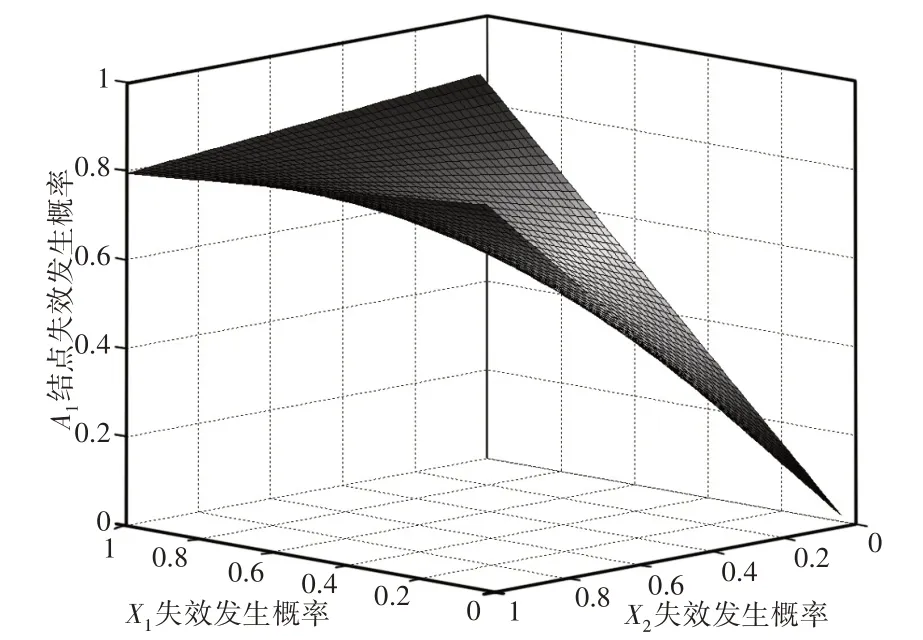
图8 X1、X2失效发生对失效结点A1的影响Fig.8 The Influence of the Failure of X1 and X2 on the Failure Node A1

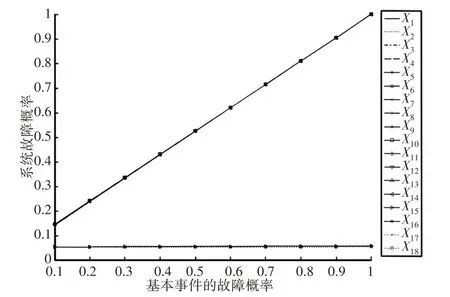
图9 各种失效影响因素对轴承失效的影响Fig.9 The Influence of Various Failure Factors on the Bearing Failure

4 结论

（1）基于Bayes网络进行高性能滚动轴承失效影响因素可靠性评估可避开不交化计算，省略最小割集的求解，分析过程直观、简化，效率高。（2）运用Bayes网络不仅可准确评估顶事件发生的概率，而且可以评估任意中间结点和顶事件发生时轴承失效影响因素的条件贡献概率，进而找出轴承使役失效的主因，为其延寿、优化设计提供重要理论依据。