负载变化对纯电动货车驱动控制策略的影响

王程玉，林慕义，2，吴柯桐，陈 勇，2

（1.北京信息科技大学机电工程学院，北京 100192；2.北京电动车辆协同创新中心，北京 100192）

1 引言

随着物流业的迅速发展，城市中货车的数量逐渐增多，新能源货车的研究开发工作变得尤为重要。纯电动货车作为新能源货车中发展最成熟，应用最广泛的一种，具有良好的市场基础。

目前，国内外学者对纯电动汽车驱动控制策略的研究有很多，通常以整车驱动的工作模式为基础[1]、针对纯电动汽车加速和起步工况[2，4，7]，建立纯电动汽车的扭矩补偿算法，使纯电动汽车不同工况及模式下电机输出的扭矩得到调节和补偿，最后达成提升整车动力性和经济性，并保证整车加速性能的效果；不过常规的驱动控制策略往往针对部分工况及参数进行设计和优化，并不能满足纯电动货车负载变化较大的情况。

针对常规控制策略中忽视的问题，依据纯电动货车负载大幅变化对电机输出扭矩的影响和加速踏板行程及其变化率所反映的驾驶意图，制定纯电动货车的驱动控制策略；将在实车中采集的数据和仿真数据进行对比，对CRUISE中搭建的整车模型进行验证；并在不同负载情况下，利用MATLAB和Cruise平台进行联合仿真。

2 纯电动货车整车基本参数

纯电动货车整车参数及对应数值，如表1所示。

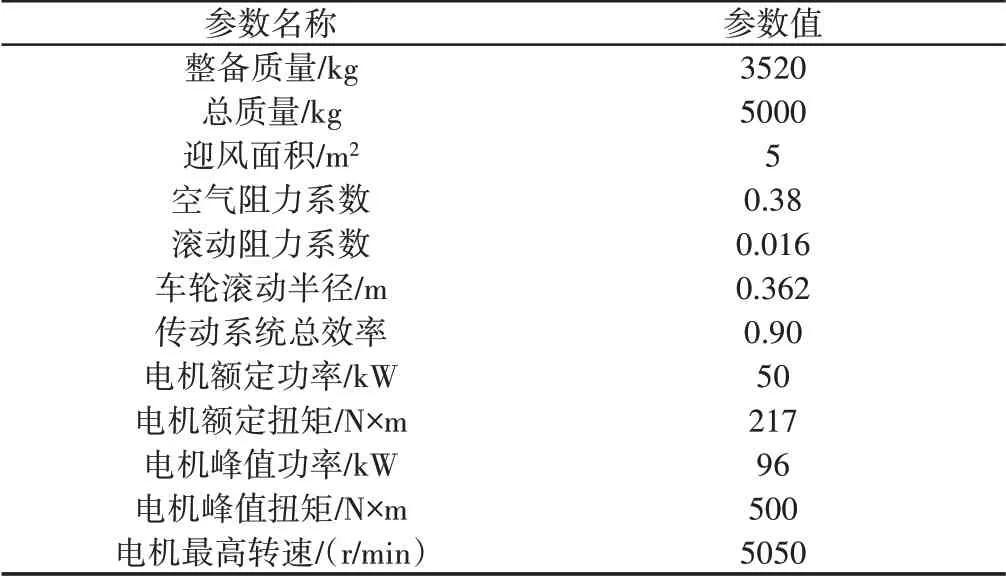
表1 整车参数Tab.1 Vehicle Parameters

3 驱动控制策略

3.1 基于加速踏板开度和电机转速制定基准扭矩

电机作为纯电动货车唯一的动力源，其性能直接决定着整车的动力性，电机输出不同的转速，其输出的最大扭矩也随之改变。驾驶员通过加速踏板的开度间接控制着电机输出的扭矩和功率，根据加速踏板开度和电机扭矩负荷系数之间的函数关系可将加速踏板控制策略分成三类：硬踏板控制策略（上凸型）、软踏板控制策略（下凹型）、线性踏板控制策略。其中线性踏板控制策略比另外两种策略更能直观的反映驾驶员意图，更符合此次设计需要，与线性踏板控制策略对应的加速踏板开度与扭矩负荷系数的函数关系，如图1所示。

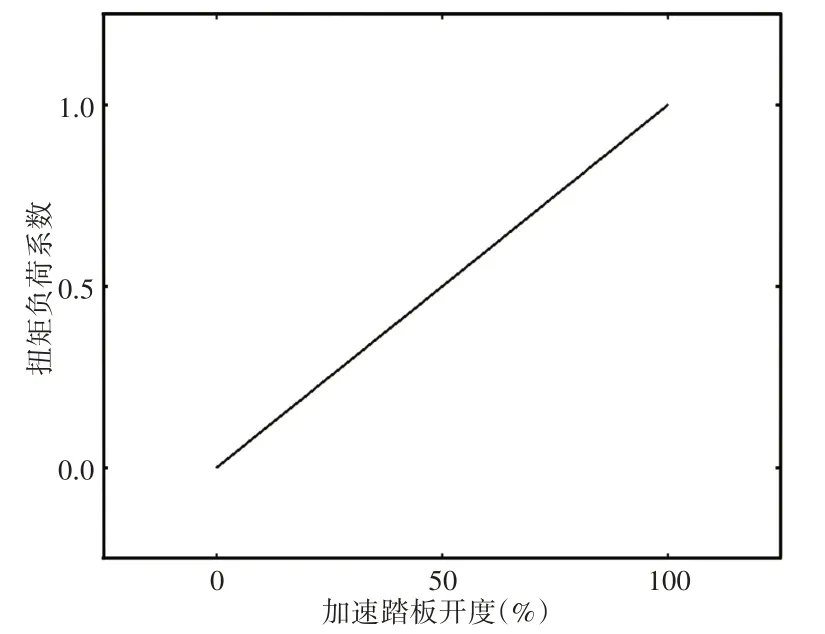
图1 线性函数关系Fig.1 Linear Function Relationship

结合纯电动货车电机的外特性曲线，制定基准扭矩，即不同加速踏板开度下，纯电动货车的动力特性图，如图2所示。

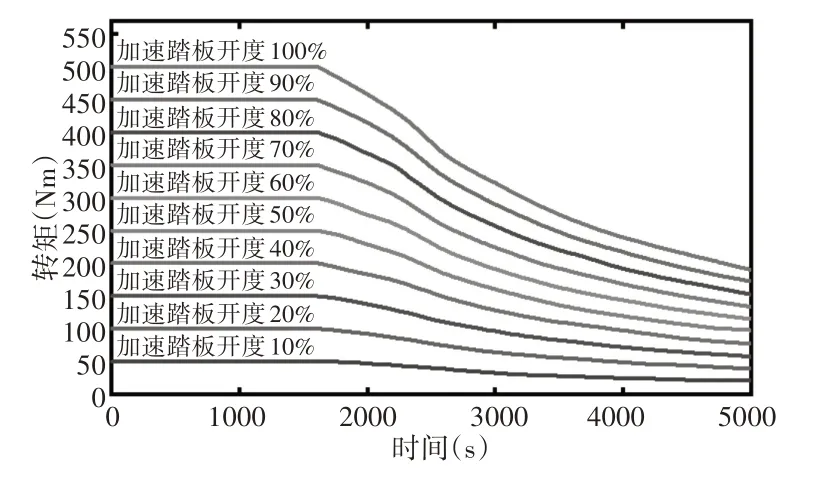
图2 基准扭矩曲线图Fig.2 Reference Torque Curve

某一时刻电机基准扭矩，如式1所示：

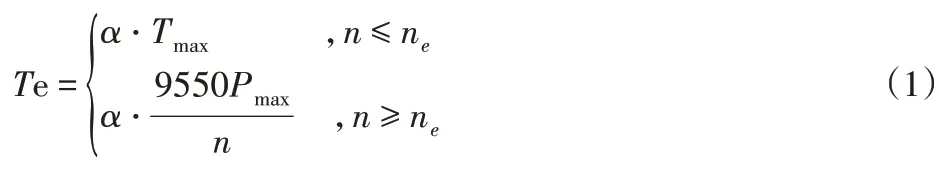
式中：ɑ—扭矩符合系数；

Tmax—当前转速下最大输出扭矩；

Pmax—电机最大功率；

ne—电机额定转速；

n—电机实际转速。

3.2 基于负载变化的驱动控制策略

纯电动货车在行驶过程中根据加速踏板开度对应的扭矩负荷系数和电机转速确定基准扭矩，根据电池SOC、车速V、加速度du/dt、加速踏板开度进行模式判断；通过模糊控制策略对输出扭矩进行补偿，弥补因负载变化输出扭矩无法满足实际工况的需求，扭矩补偿控制算法，如图3所示。为了使控制策略可以根据货车负载的变化产生不同的响应，引入负载变化的数据模拟量。

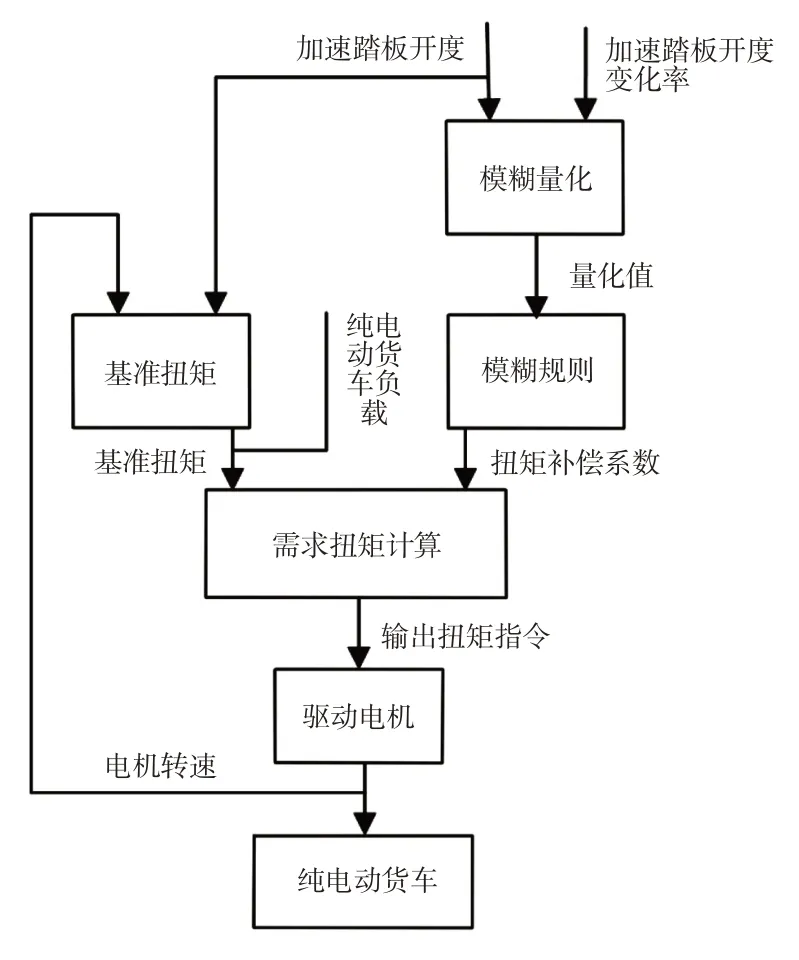
图3 扭矩控制算法图Fig.3 Torque Control Algorithm Diagram

3.3 模糊控制器设计

加速踏板开度与电机输出的扭矩成一定的函数关系，而且一旦确定将无法更改，只能通过驾驶员后期的反复操作使货车满足驾驶员的预期车速，我们引入以加速踏板开度和加速踏板变化率为输入，以扭矩的补偿系数k为输出的模糊控制器，对电机输出扭矩进行补偿修正。加速踏板开度的模糊子集为｛VS，S，M，B，VB｝，即{很小，小，中，大，很大}；加速踏板开度变化率的模糊子集为：｛VB，N，M，P，PB｝，即｛较小，小，中，大，较大｝；扭矩补偿系数k的集合为｛VB，VM，N，M，P，MP，MB｝，即｛大减速，中减速，减速，中，加速，中加速，大加速｝。加速踏板开度的论域范围为［0，1］；加速踏板变化率的论域范围为［-5，5］；扭矩补偿系数的论域范围为［0.5，1.5］。该模糊控制器的隶属度函数，如图4所示。模糊控制规则，如表2所示。

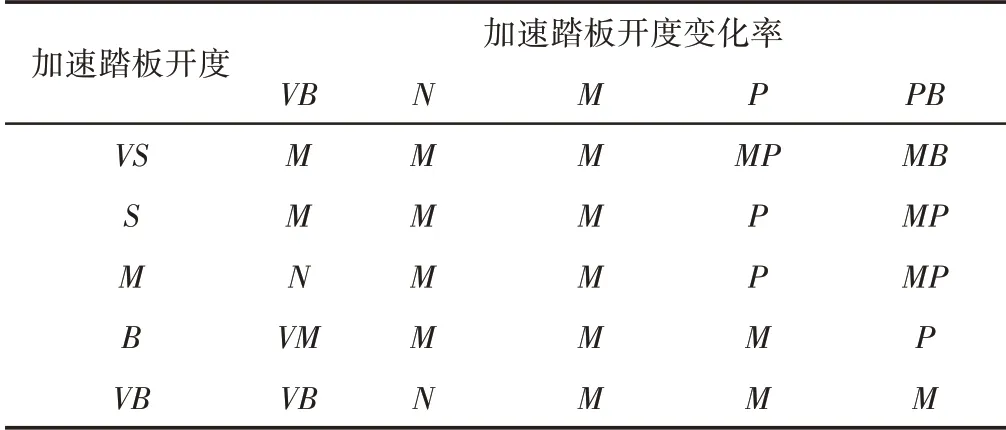
表2 模糊规则Tab.2 Fuzzy Rule

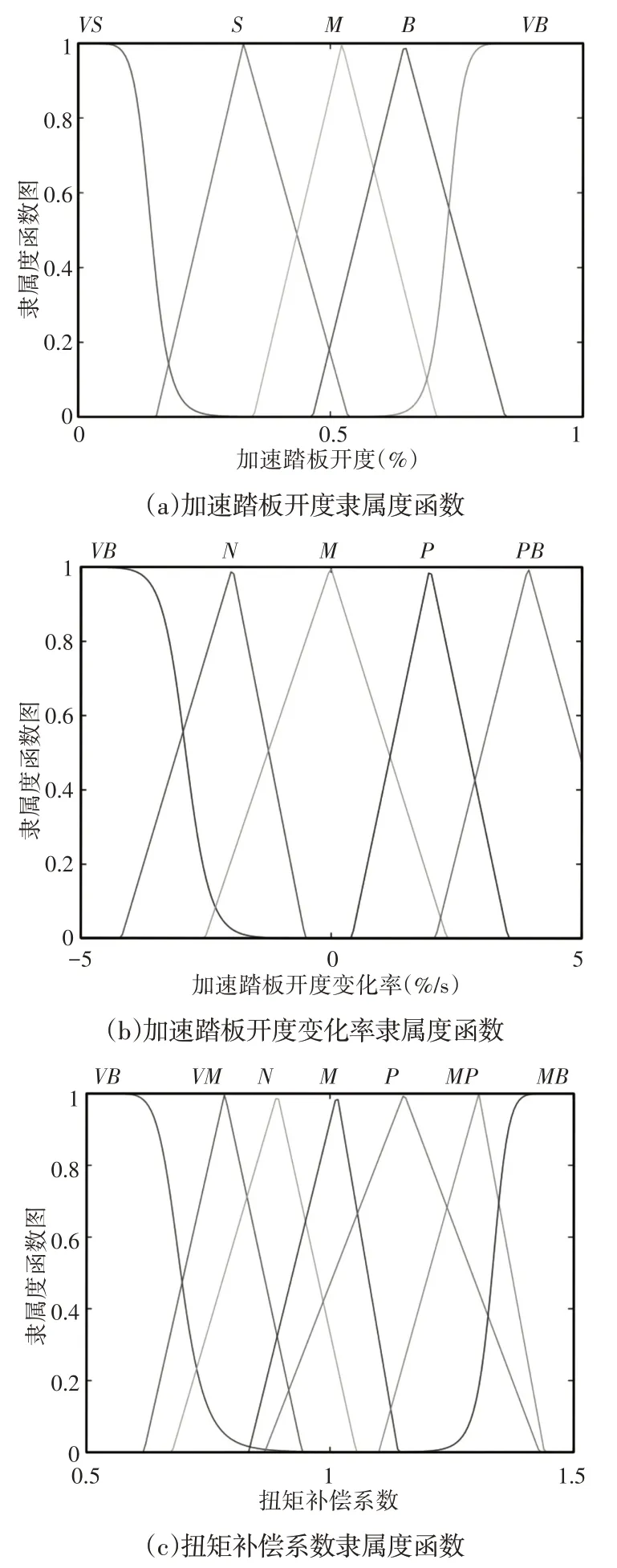
图4 模糊控制器的隶属度函数Fig.4 Membership Function of Fuzzy Controller

4 整车模型验证

纯电动货车在行驶过程中通过CAN通讯收集信号并将整车控制器的指令传输到各控制单元，目前较为常用的网络标准是博世推出的CAN，纯电动汽车一般会设置CAN通讯接口，将车辆的信息输出到测试终端，如图5所示。

图5 实车CAN通讯接口Fig.5 Real Vehicle CAN Communication Interface

截取实车（0～74）km/h满负荷加速时车速随时间变化情况，并将其与AVL Cruise中的仿真数据进行对比，如图6所示，从图中可以看出，仿真的速度曲线与试验速度曲线趋势相同，加速时间近似，由于实际测试中驾驶员操控和通讯延时，所以在加速前5s实验数据有明显的延时，忽略驾驶员操控和部件通信延时之后，初步证明了整车仿真模型的可靠性和有效性。

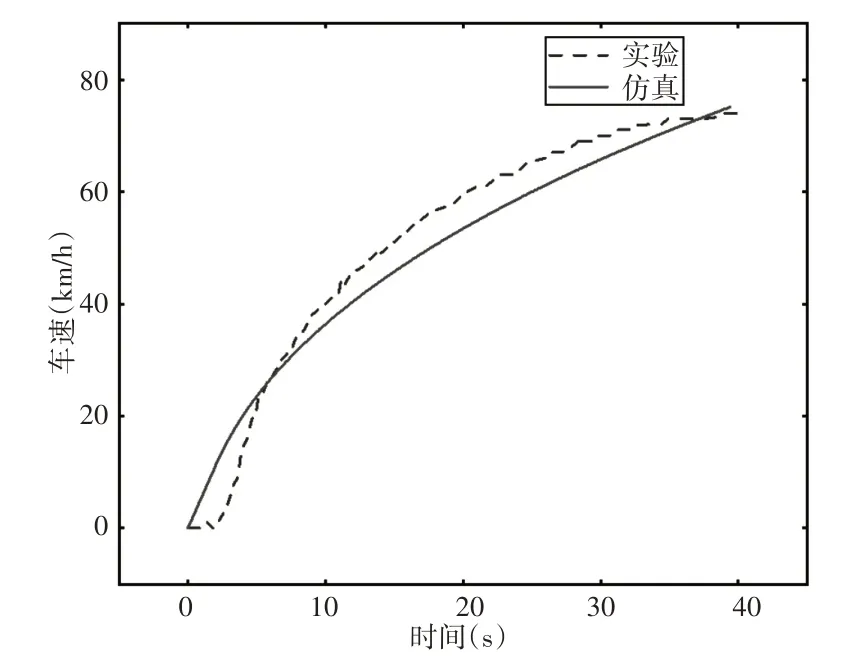
图6 实车与仿真车速对比Fig.6 Real Car and Simulation Speed Comparison

5 仿真结果分析

针对控制策略的仿真验证分为两个方面：（1）基于负载变化对整车性能进行分析；（2）加入控制策略前、后对扭矩和能耗的影响。

在不同负载情况下，电机扭矩补偿系数和电机输出扭矩随时间的变化情况，如图7所示。由图可以得出负载越高时，电机扭矩补偿系数越大、电机输出扭矩越大，验证了控制策略中模糊控制器的有效性。

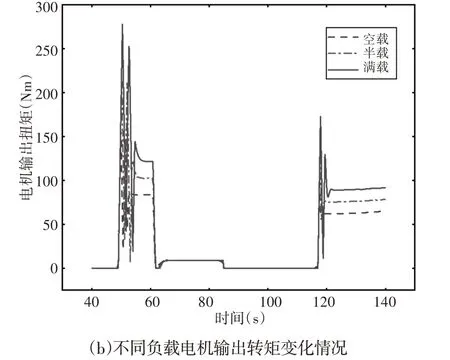
图7 不同负载时仿真数据对比Fig.7 Comparison of Simulation Data at Different Loads

加入驱动控制策略前、后，电机输出扭矩和整车能耗随时间变化的情况，如图8所示。加入控制策略之后电机输出扭矩的峰值明显增大，验证了控制策略对电机扭矩的补偿效果；图8（b）为NEDC循环工况电机输出能量随时间变化的情况，无控制策略时电机输出能量共为5872kJ，加入控制策略之后电机输出能量共为4912kJ，同比能量消耗下降16.34%。

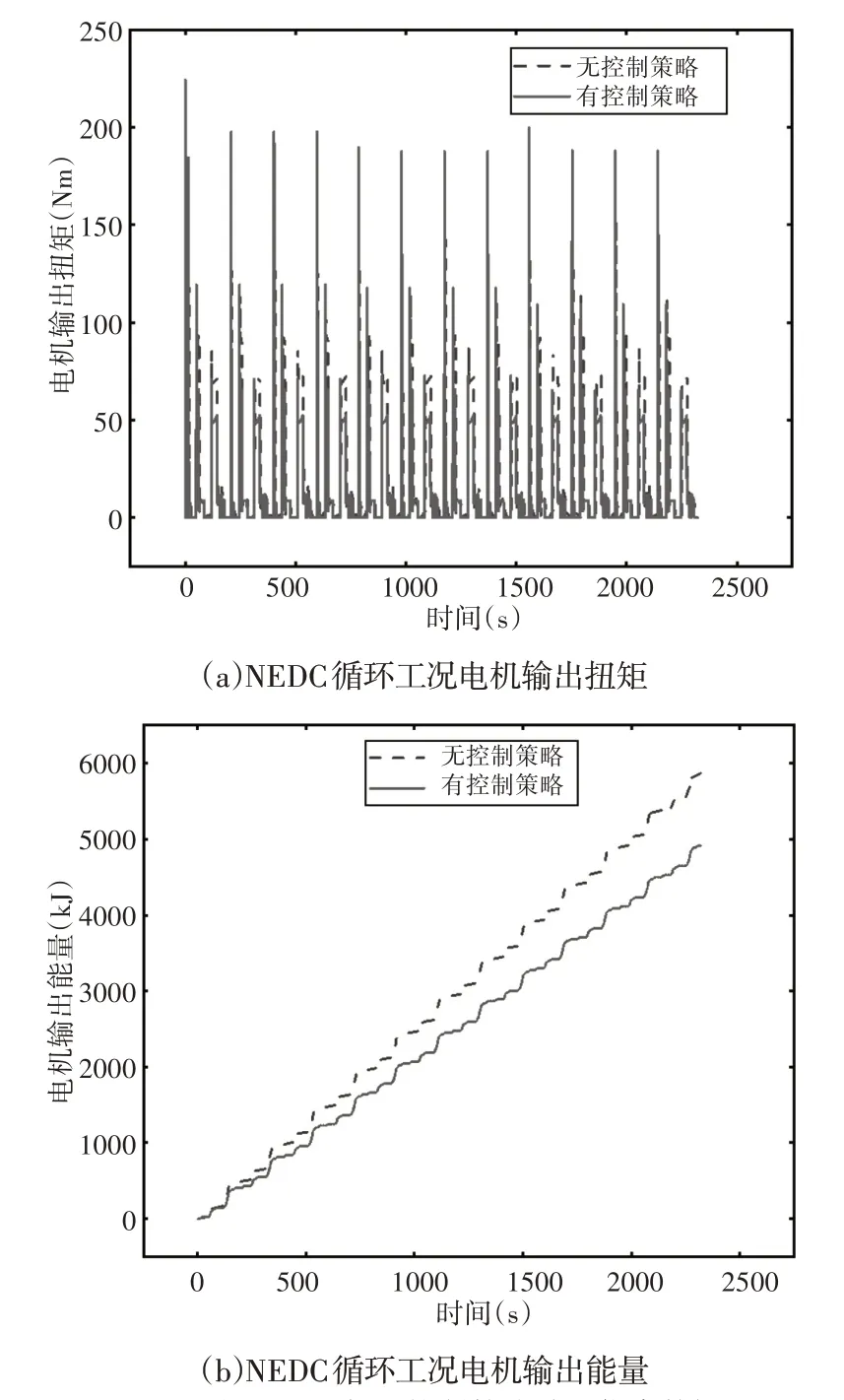
图8 NEDC循环工况加入控制策略前后仿真数据对比Fig.8 Comparison of Simulation Data Before and After Adding Control Strategy Under NEDC Cycle Condition

6 结论

针对纯电动货车负载的变化，提出了一种纯电动货车驱动控制策略；通过实车数据与仿真数据对比保证了整车模型的可靠性和有效性；使用MATLAB/SIMULINK和AVL Cruise联合仿真对控制策略进行验证；结果表明：从提升整车加速性能的角度来看，提出的控制策略可以根据不同负载情况对扭矩起到补偿作用，从而使电机输出转矩较快达到加速踏板所对应的需求扭矩；与加入控制策略之前相比，电机在NEDC循环工况下输出的能量下降了16.34%，整车的经济性得到了相应的改善。