考虑台后不平衡土压力下整体桥H型钢桩基-土相互作用内力计算方法

2022-02-23单玉麟黄福云周桂吉易志宏陈宝春

建筑科学与工程学报 2022年1期

单玉麟，黄福云，周桂吉，易志宏，陈宝春

(1. 福州大学土木工程学院,福建福州 350108； 2. 东南大学土木工程学院,江苏南京 211189；3. 四川省公路规划勘察设计研究院有限公司,四川成都 610041)

0 引言

整体式桥台无缝桥(简称整体桥)是指上部结构(主梁、桥面板以及桥头引板)和下部结构(桥台、桩基础)连成整体的桥梁[1]。整体桥因较好的整体性、耐久性和强震作用下不易落梁的优点而被广泛应用于欧美日等国[2-5]，但是整体桥主梁在外界温度、混凝土收缩徐变以及地震作用下会产生水平往复变形。这些往复变形由主梁向两端的桥台及台底桩基础传递，并将进一步作用于台后土体，引起复杂的结构-土相互作用[6-10]。为了较好地适应该水平往复变形，整体桥台底桩基础常采用H型钢桩基[11-12]。

目前，许多学者对平衡土压力下整体桥H型钢桩基的变形和受力性能进行了研究[13-16]，结果表明：H型钢桩表现出更好的弹塑性变形能力、延性和耗能能力。然而，由于台后填土的存在，整体式桥台台底桩基础一般处于不平衡的土压力状态。Frosch等[17]在整体式桥台-H型钢桩拟静力试验基础上，建立了基于位移的地震响应设计方法与评价指标。Burdette等[18]开展了H型钢桩支撑桥台的水平受荷试验，结果表明：相比早期试验，较宽的桥台能承受更大的水平变形。黄福云等[19-21]开展了不同加载工况下桥台-H型钢桩-土相互作用拟静力试验研究，结果表明：整体桥H型钢桩的水平变形和弯矩均与处于平衡土压力状态下的桩基存在较大的差异。安泽宇[22]对6个桥台-H型钢桩构件进行了拟静力试验，研究表明，H型钢桩强弱轴布置方向对整体桥抗震性能有较大的影响。同时，由于车辆重载、台后填土压实度以及台后不同填料(砂或碎石)等作用，将进一步造成台后不平衡土压力的变化。

目前，中国桩基计算常采用“m”法[23]、“p-y”曲线法[24]和基于位移的桩-土相互作用计算方法[25]。“m”法是基于线弹性与小变形的设计理念，难以满足地震作用下整体式桥台桥梁桩基的非线性、大变形要求；“p-y”曲线法是基于大变形的理念，充分考虑了桩-土相互作用的非线性和土的塑性影响；基于位移的桩-土相互作用计算方法是假定桩顶剪力与桩周土抗力是平衡的。上述方法均忽略了台后不平衡土压力对桩基受力性能的影响，其计算方法是否适用于整体桥还需进一步研究。

本文在文献[26]开展的台后填土作用下整体式桥台-H型钢桩-土相互作用和大不平衡土压力下(台后土表面均布荷载增大了3.81 kPa)整体式桥台-H型钢桩-土相互作用拟静力试验研究的基础上，提出了考虑台后不平衡土压力下整体桥桩基-土相互作用的内力计算方法，为相关规范的制订提供借鉴和参考。

1 试验简介

1.1 试件制作

文献[26]中设计并制作了2个桥台-H型钢桩试件，编号分别为AHP和LAHP。AHP模型为台后填土作用下整体式桥台-H型钢桩-土相互作用，如图1(a)所示；LAHP模型为大不平衡土压力下整体式桥台-H型钢桩-土相互作用，如图1(b)所示。表1给出了AHP和LAHP试件的详细尺寸。桥台竖向纵筋分别采用φ12与φ8的HRB335带肋钢筋，箍筋采用φ6的HRB335光圆钢筋。钢筋屈服强度为337 MPa，极限强度为454 MPa；H型钢桩均采用Q235钢材，抗压强度为215 MPa，屈服强度为238 MPa，弹性模量为208 GPa。

图1 AHP和LAHP模型(单位:mm)Fig.1 AHP and LAHP Models (Unit:mm)

表1 AHP和LAHP试件的详细尺寸Table 1 Detail Dimensions of AHP and LAHP Specimens

试验土箱采用组合拼装，其长3 m，宽2 m，高4 m，壁厚10 mm。试验用砂采用闽江砂土，密度为1.50 g·cm-3，相对密度为53%，内摩擦角为35°，含水率为1.3%，孔隙比为0.59，黏聚力为0 kPa，平均标准贯入度为11。

1.2 测点的布置与加载

文献[26]中AHP和LAHP模型布置有应变片和土压力计。H型钢桩共布置26个应变片，从土表面开始以200 mm为间距进行布置，编号为S1～S26，如图2(a)所示。H型钢桩共布置20个土压力计，从土表面开始分别以200 mm和400 mm为间距进行布置，编号为T1～T20；台后土压力计共布置5个，从台后土表面开始，土压力计埋深分别位于0.125、0.375、0.625、0.875、1.0 m处，编号为T21～T25，如图2(b)所示。

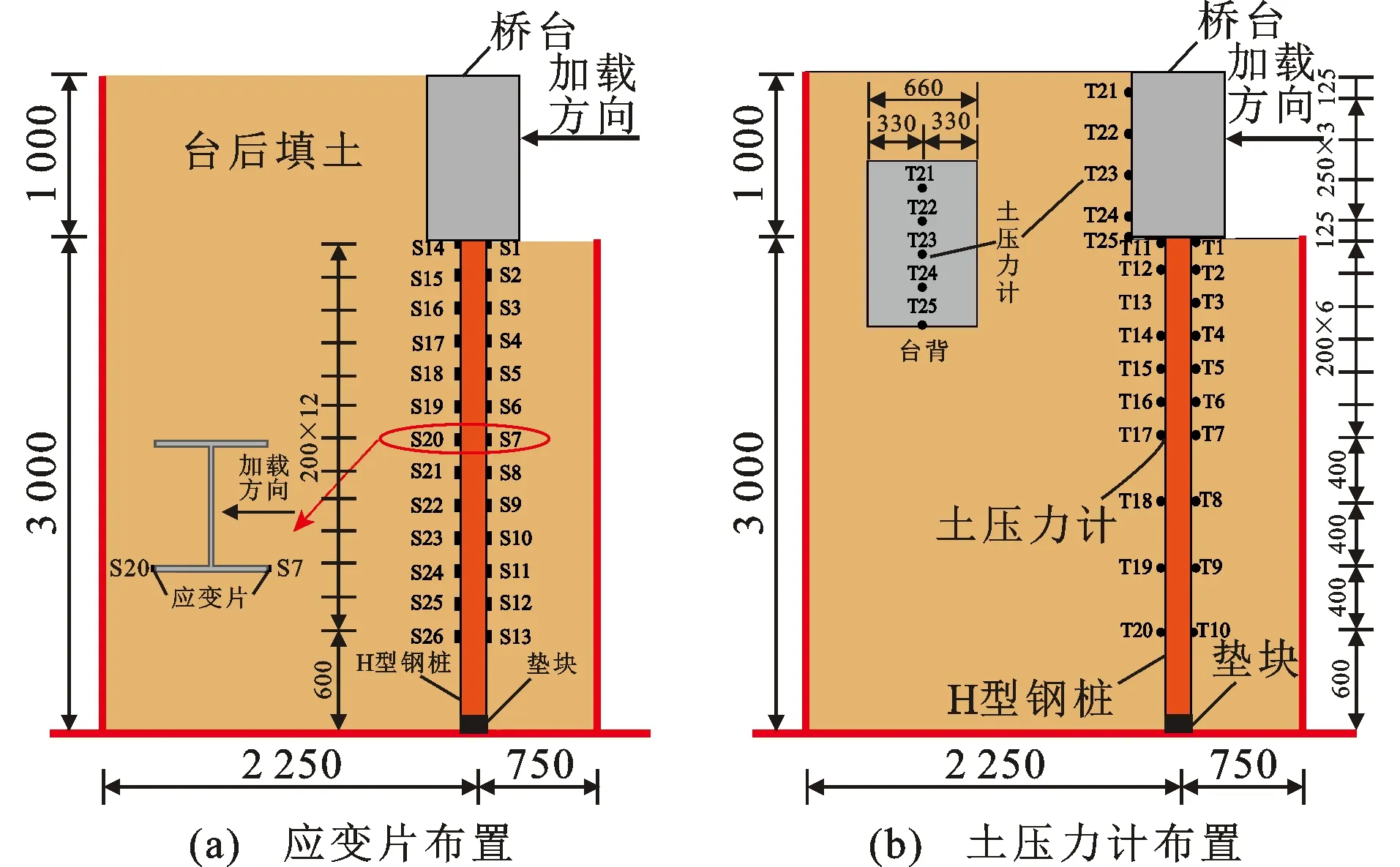
图2 应变片和土压力计布置(单位：mm)Fig.2 Layout of Strain Gauges and Earth Pressure Cells (Unit:mm)

拟静力试验采用福州大学MTS电液伺服加载系统施加低周往复水平位移荷载。试验过程中采用位移控制分级加载。每级以2 mm的位移为增量逐级加载，加载至16 mm时终止，加载频率为1 Hz，每级荷载循环3次，且每级加载持荷30 s。如无特殊说明，均取每级荷载第2次循环的试验结果进行分析。本文定义往台后土方向施加位移荷载为正方向，往河跨方向施加为负方向。

2 桥台内力计算

2.1 计算方法

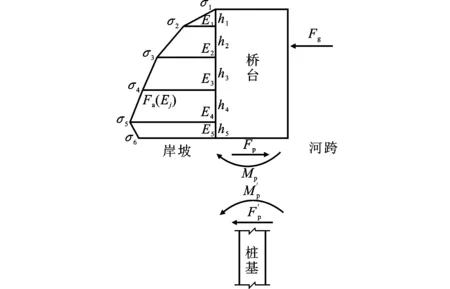
图3 正向加载时台底(桩顶)剪力和弯矩计算模型Fig.3 Calculation Model of Shear Force and Bending Moment of Abutment Bottom (Pile Top) Under Positive Loading

台后土压力合力可按公式(1)计算。

(1)

式中：Fa为台背处台后土压力合力，规定Fa朝岸坡侧为正，朝河跨侧为负；Ej为桥台第j层土压力；n为总土层数；σj为第j层土压力；σj+1为第j+1层土压力；hj为桥台第j层土层高度；b为桥台宽度。

剪力平衡方程如公式(2)所示。

Fa+Fg+Fp=0

(2)

式中：Fg为MTS加载力，规定MTS推力为正(朝岸坡)，拉力为负(朝河跨)；Fp为台底剪力，并以图示箭头方向为正。

台背处台后土压力合力Fa对台底的弯矩可根据公式(3)计算。

Ma=Fahz

(3)

式中：Ma为台背土压力合力对桥台底部的弯矩；hz为台背土压力合力Fa的作用点至桥台底部的距离，一般取桥台高度的1/3。

MTS作用力对台底的弯矩可由公式(4)计算。

Mg=Fgh0

(4)

式中：Mg为MTS作用弯矩；h0为MTS作用力Fg的作用点位置至桥台底部的距离，h0=0.65h，h为桥台高度。

弯矩平衡方程如公式(5)所示。

Ma+Mg+Mp=0

(5)

式中：Mp为台底弯矩，规定台底弯矩顺时针旋转时为正。

2.2 各理论方法下台底剪力和弯矩比较

2.2.1 台底剪力和弯矩分析

图4为AHP模型台底剪力和弯矩比较，图5为LAHP模型台底剪力和弯矩比较。

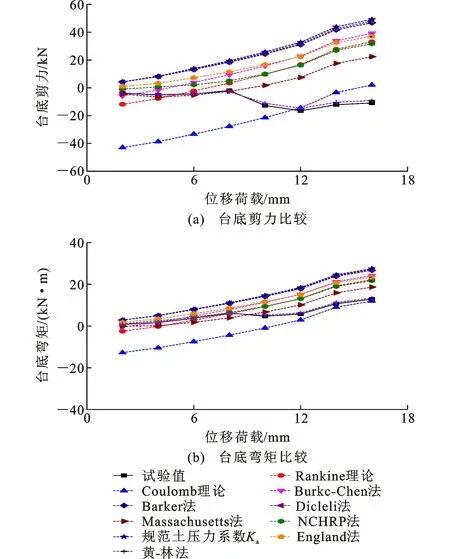
图4 AHP模型台底剪力和弯矩比较Fig.4 Comparison on Shear Force and Bending Moment of Abutment Bottom for AHP Model

图5 LAHP模型台底剪力和弯矩比较Fig.5 Comparison on Shear Force and Bending Moment of Abutment Bottom for LAHP Model

从图4和图5可知，各理论计算得到的AHP和LAHP模型台底剪力和弯矩随着位移荷载的增加基本呈线性变化，但各计算结果之间存在较大差异，与试验值也存在较大的偏差。Coulomb理论计算值和Rankine理论计算值随着位移荷载的增大先负向减小，后正向增大；其他理论计算值均正向增大；试验值基本介于各理论计算值之间。采用《公路桥涵设计通用规范》(JTG D60—2015)中主动土压力系数计算得到的台底剪力和弯矩均为正向最大。AHP模型台底最大剪力和弯矩分别为49.26 kN和27.56 kN·m；LAHP模型台底最大剪力和弯矩分别为57.38 kN和32.02 kN·m；LAHP模型台底最大剪力和弯矩均为AHP模型的1.2倍。采用Coulomb理论(被动土压力系数)得到的剪力和弯矩均为负向最大。AHP模型台底最大剪力和弯矩分别为-42.89 kN和-12.74 kN·m；LAHP模型台底最大剪力和弯矩分别为-41.88 kN和-12.19 kN·m；LAHP模型台底最大剪力和弯矩略小于AHP模型的。分析其原因是因为当位移荷载较小时，土压力也较小，此时采用Coulomb理论结果偏差最大，而采用其他方法偏差相对较小；当位移荷载较大时，土压力较大，此时采用规范计算结果偏差最大，而采用Coulomb理论计算偏差最小。

从图4(a)可知：当位移荷载不超过8 mm时，AHP模型试验值与Massachusetts法和黄-林法计算值较为吻合；当位移荷载超过8 mm时，除黄-林法计算值与AHP模型试验值较为吻合外，其他各种经典理论计算值及其变化规律均与试验值存在较大的差异。

从图4(b)可知：当位移荷载不超过8 mm时，AHP模型试验值与NCHRP法和黄-林法计算值较为吻合；当位移荷载在8～14 mm范围内时，AHP模型试验值与黄-林法计算值较为吻合；当位移荷载大于14 mm时，试验值与黄-林法和Coulomb理论计算值较为吻合。

从图5(a)可知：当位移荷载在2～4 mm时，LAHP模型试验值与Massachusetts法和黄-林法计算值较为吻合；当位移荷载在4～6 mm范围内时，LAHP模型试验值与Massachusetts法、Rankine理论和黄-林法计算值较为吻合；当位移荷载在6～12 mm范围内时，LAHP模型试验值介于Massachusetts法和Coulomb理论计算值之间；当位移荷载大于12 mm时，LAHP模型试验值大于Coulomb理论和黄-林法计算值。

从图5(b)可知：当加载位移不超过8 mm时，LAHP模型试验值与NCHRP法和黄-林法计算值较为吻合；当位移荷载在8～12 mm范围内时，LAHP模型试验值与Massachusetts法和黄-林法计算值较为吻合；当位移荷载在12～14 mm范围内时，LAHP模型试验值与黄-林法计算值较为吻合；当位移荷载在14～16 mm范围内时，LAHP模型试验值与Coulomb理论计算值较为吻合。

2.2.2 台底剪力和弯矩比较

图6为AHP模型和LAHP模型台底剪力和弯矩比较。

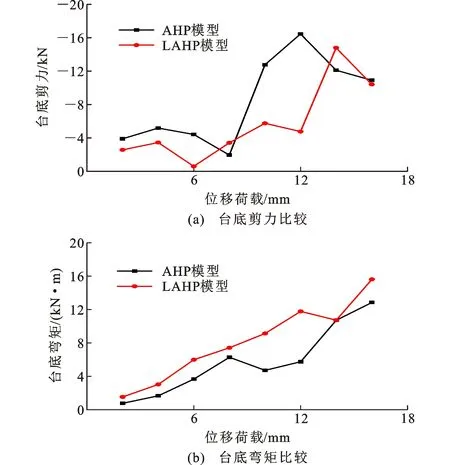
图6 AHP和LAHP模型台底剪力和弯矩比较Fig.6 Comparison on Shear Force and Bending Moment of Abutment Bottom for AHP and LAHP Models

从图6(a)可知：LAHP模型台底剪力整体上小于AHP模型；当位移荷载为12 mm时，LAHP模型的台底剪力为-4.77 kN，AHP模型的台底剪力为-16.46 kN，前者为后者的0.3倍。

从图6(b)可知：随着位移荷载的增加，AHP和LAHP模型台底弯矩逐渐增大；LAHP模型台底弯矩整体上大于AHP模型的。当位移荷载为16 mm时，LAHP和AHP模型台底弯矩分别为15.60、12.84 kN·m，前者为后者的1.2倍。

综上所述，台后堆载(大不平衡土压力)对整体桥台底的剪力和弯矩产生较大影响，台后堆载会减小台底剪力和增大台底弯矩。分析其原因是因为正向加载时，LAHP模型台背处的土压力(台后土压力)远大于AHP模型。

3 桩基内力计算方法

3.1 桩身弯矩和剪力分析

由于台底剪力和弯矩即为桩顶的剪力和弯矩，也即桩顶的外力边界条件。因此，当采用不同的台后土压力理论方法计算得到的台底(桩顶)弯矩与剪力相差较大时，边界条件也就会相差较大，从而会极大地影响桩身内力的计算。首先基于现有的台后土压力理论和试验数据得到桩顶的外力，然后采用“m”法计算桩身弯矩和剪力，最后将不同的理论计算值和试验值进行比较。

《公路桥涵地基与基础设计规范》(JTG 3363—2019)[23]给出了按“m”法计算桩身弯矩M(z)和桩身剪力Q(z)的方法，如公式(6)、(7)所示。

(6)

Q(z)=y0A4α3EI+φ0B4α2EI+MpC4α+FpD4

(7)

(8)

(9)

图7和图8分别为在各种理论计算下AHP和LAHP模型桩身最大弯矩和剪力比较。从图7和图8可知，AHP和LAHP模型桩身最大弯矩和剪力值随位移荷载的增加逐渐增大，但表现不尽相同。

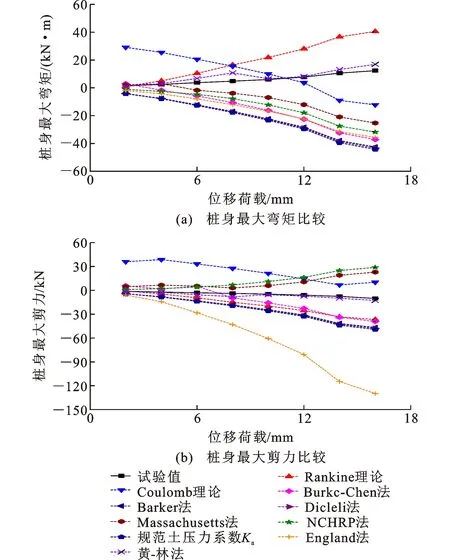
图7 AHP模型桩身最大弯矩和剪力比较Fig.7 Comparison on Maximum Bending Moment and Shear Force of Pile Body for AHP Model

图8 LAHP模型桩身最大弯矩和剪力比较Fig.8 Comparison on Maximum Bending Moment and Shear Force of Pile Body for LAHP Model

从图7(a)可知：AHP模型试验值与Rankine理论和黄-林法计算值均随着位移荷载的增大正向增大；Coulomb理论计算值随着位移荷载的增大先正向减少，后负向增大；其他理论计算值均为负向增大；AHP模型试验值与黄-林法计算值较吻合。

从图7(b)可知：Massachusetts法和NCHRP法计算值随着位移荷载的增大正向增大；Coulomb理论计算值随着位移荷载的增大正向减少；其他理论计算值均为负向增大；AHP模型试验值与黄-林法计算值较吻合。

从图8(a)可知：LAHP模型试验值随着位移荷载的增大正向增大；Coulomb理论计算值随着位移荷载的增大先正向减小，后负向增大；其他理论计算值均为负向增大；LAHP模型试验值均与各理论计算值相差较大。

从图8(b)可知：LAHP模型试验值与Massachusetts法、NCHRP法和黄-林法计算值均随着位移荷载的增大正向增大；Coulomb理论计算值随着位移荷载的增大正向减小；其他理论计算值均为负向增大；当位移荷载在0～8 mm范围内时，LAHP模型试验值与Rankine理论、NCHRP法和黄-林法计算值较为吻合；当位移荷载超过8 mm时，LAHP模型试验值在Massachusetts法、黄-林法和Coulomb理论计算值之间波动。

3.2 桩身弯矩和剪力比较

图9为AHP和LAHP模型桩身最大弯矩和剪力比较。

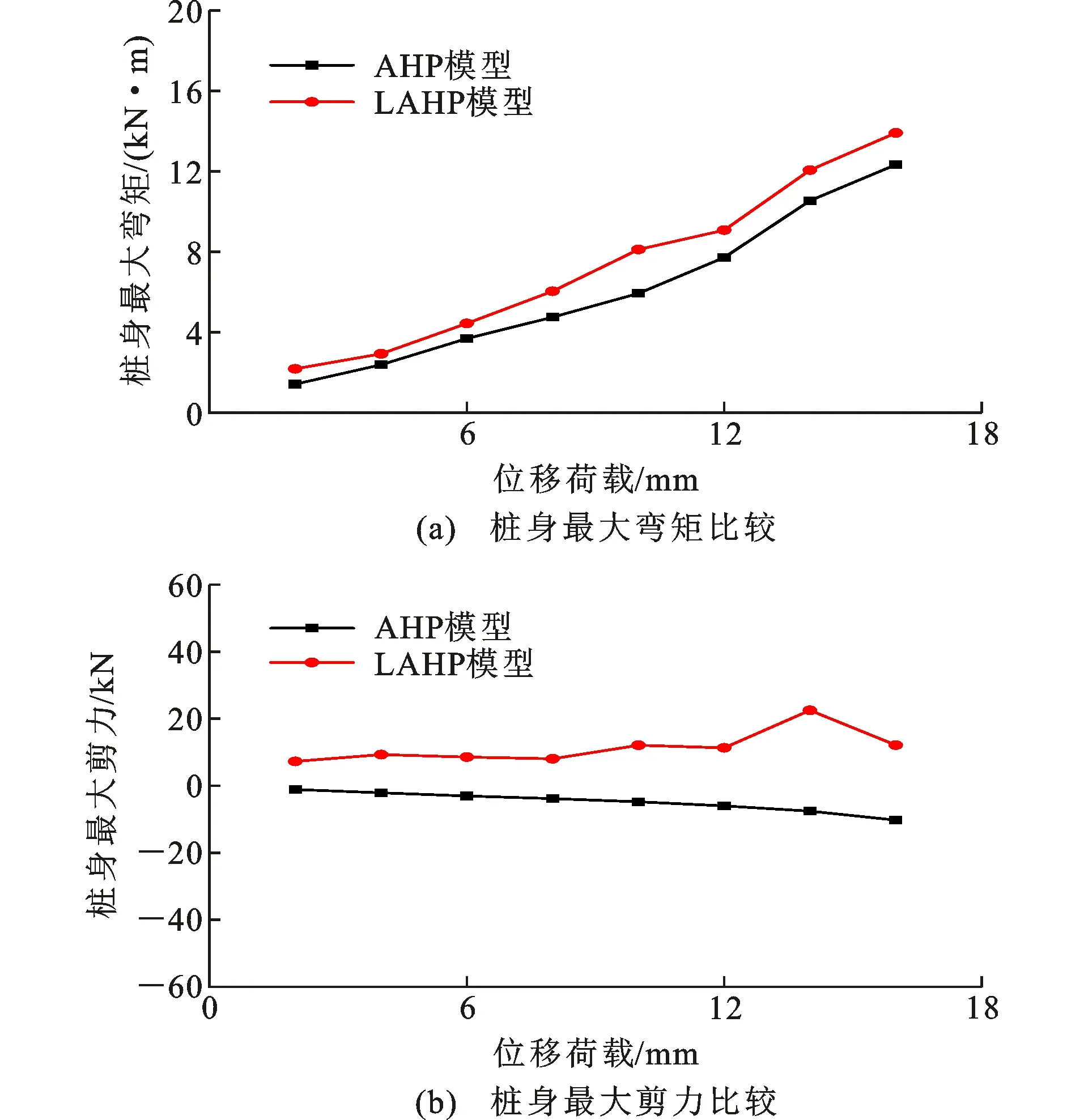
图9 AHP和LAHP模型桩身最大弯矩和剪力比较Fig.9 Comparison on Maximum Bending Moment and Shear Force of Pile Body for AHP and LAHP Models

从图9(a)可知：随着位移荷载的增大，AHP和LAHP模型桩身最大弯矩逐渐增大；LAHP模型桩身最大弯矩整体上大于AHP模型的；当位移荷载为16 mm时，LAHP和AHP模型桩身最大弯矩分别为13.92、12.34 kN·m，前者为后者的1.1倍。

从图9(b)可知：LAHP和AHP模型桩身最大剪力分布规律存在较大的差异；随着位移荷载的增加，LAHP模型桩身最大剪力整体上正向增大，而AHP模型桩身最大剪力负向增大；LAHP模型的桩身最大剪力远大于AHP模型的；当位移荷载为14 mm时，LAHP和AHP模型桩身最大剪力分别为22.50、-7.57 kN，前者为后者的3.0倍，且两者桩身最大剪力方向相反。

综上所述，台后堆载(大不平衡土压力)均会增大整体桥桩身的弯矩和剪力。分析其原因是因为台后堆载的存在，正向加载时桩基更难正向移动，进而造成桩基的内力更大。