边坡对铁路桥台抗震性能的影响分析

王 义，陈兴冲，张熙胤，丁明波，刘正楠，杨晨吟

(兰州交通大学 土木工程学院，兰州 730070)

桥台作为桥梁结构重要的组成部分对整个结构的使用和安全举足轻重[1].桥台不仅起到支撑上部结构及衔接路堤的作用，同时还能抵抗台后土压力.然而，以往研究表明：正常使用情况下桥台具有较好的工作性能，但地震作用下由于桥台-周围土体的相互作用，使得桥台在地震中的反应变得更加复杂[2].地震时由于桥台破坏而引起桥梁破坏的现象非常普遍，国内外均有大量报道，如1995年阪神地震、2008年汶川地震及2010年东日本大地震等均造成了大量桥台受损[3-4]，因此，桥台的抗震问题引起工程界的广泛关注[5].

王海涛等[6]基于有限元数值模拟研究了液化场地中浅基础桥台的破坏机理，采用有效应力法模拟砂土的液化特性，研究了液化层位置及台顶梁重等因素对桥台位移的影响.孙治国等[7]基于汶川地震中高原大桥的桥台震害，采用ANSYS有限元软件研究了浅基础桥台受主梁撞击的破坏形态.李悦等[8]采用Newmark时程分析法研究了土-桥台-上部结构相互作用对浅基础桥台抗震性能的影响.Xie等[9]为研究浅基础桥台的抗震性能，提出了一种台背填土的概率分析模型，并采用试验验证了模型的有效性.Xu等[10]研究了全高框架整体桥台的抗震性能.文献[11-13]基于拟静力试验研究了整体式桩基础桥台的抗震性能.Khodair等[14]研究了软土区桩基础桥台的抗震性能.以上研究均是针对建造于水平地面的浅基础或桩基础桥台展开的.随着我国交通运输业的发展，建造于高陡边坡上的铁路桥台逐渐增多.由于边坡的存在往往导致桩基础的受力不同于普通桩基[15]，这使得建造于高陡边坡上的铁路桩基础桥台在台背土及边坡共同影响下的抗震性能区别于普通桥台.Vytiniotis等[16]研究了边坡上某桩支撑码头结构的地震反应，结果表明，桩支撑码头结构破坏的主要原因是土体的侧向扩展，因此必须采取相应的缓解措施来控制下坡土体的变形.另外，文献[17-20]也对建造于边坡上的桩基码头结构的抗震性能及稳定性开展了大量研究，然而，由于桩基码头的上部结构形式与桩基础桥台存在较大差异，因此地震作用下两种结构的响应也存在较大差异.

基于ABAQUS有限元分析平台，建立了铁路桩基础桥台抗震分析模型，深入研究了边坡影响下桥台的滞回曲线、骨架曲线、桩基位移、耗能能力及刚度退化等重要抗震性能指标，以期为高陡边坡地区桥台的抗震设计及理论研究提供参考.

1 桥台概况

某铁路桥台位于典型的黄土边坡上，坡底距桥台底面40 m.桥台采用2×3的群桩基础，桩基采用直径1.0 m、桩长28 m的摩擦桩.桥台台身及桩基均采用C35混凝土，边坡坡度为45°.桥台概况如图1所示，桥台尺寸及桩基布置如图2所示.

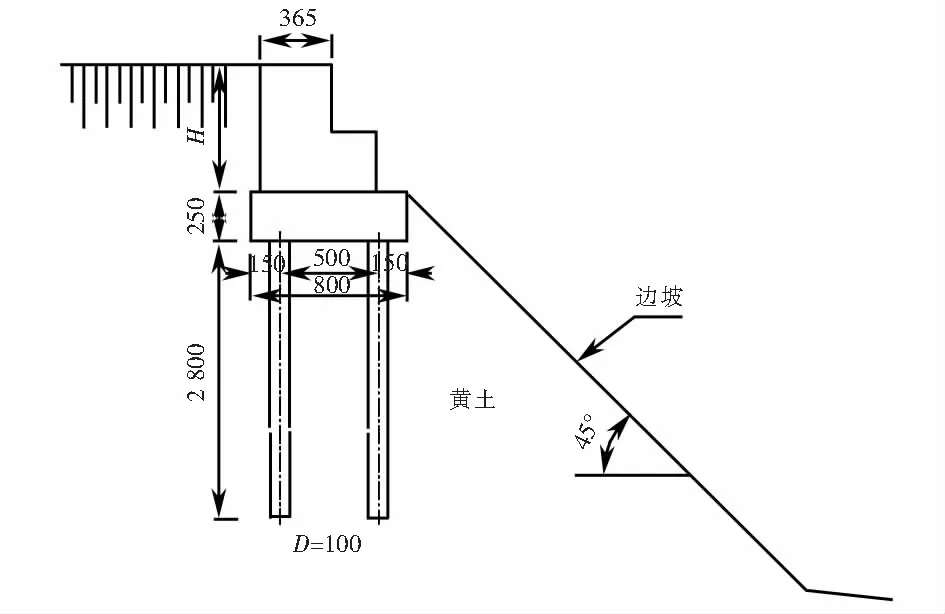
图1 桥台概况(单位：cm)Fig.1 Abutment overview (unit:cm)

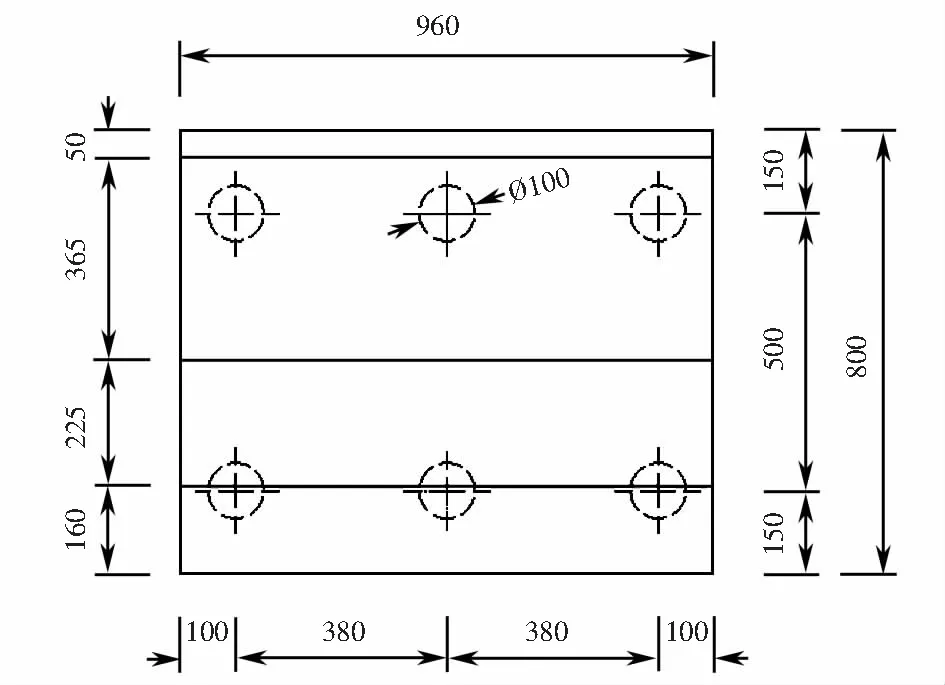
图2 桥台尺寸及桩基布置(单位：cm)Fig.2 Abutment size and pile foundation layout (unit:cm)

2 数值分析

2.1 材料本构及参数选取

基于ABAQUS有限元平台建立桩基础桥台的抗震分析模型，通过参数分析，研究有无边坡及边坡影响下不同桥台高度对桩基础桥台抗震性能的影响，建立的有限元分析模型如图3所示.桩基础和桥台混凝土选用ABAQUS提供的塑性损伤模型模拟(CDP模型)，混凝土应力-应变关系如图4所示.土体、桩基础和桥台采用三维实体单元模拟，土体材料选用Mohr-Coulomb模型模拟，土体参数如表1所列.混凝土参数如下：容重γD=23 kN/m3，弹性模量ED=3.15×104MPa.钢筋选用T3D2单元，材料采用双折线模型模拟，钢筋与混凝土间采用嵌入方式结合，钢筋采用HRB400级钢筋，材料参数如下：容重γr=7.85×103kN/m3，弹性模量ED=2.0×105MPa,泊松比νr=0.2.

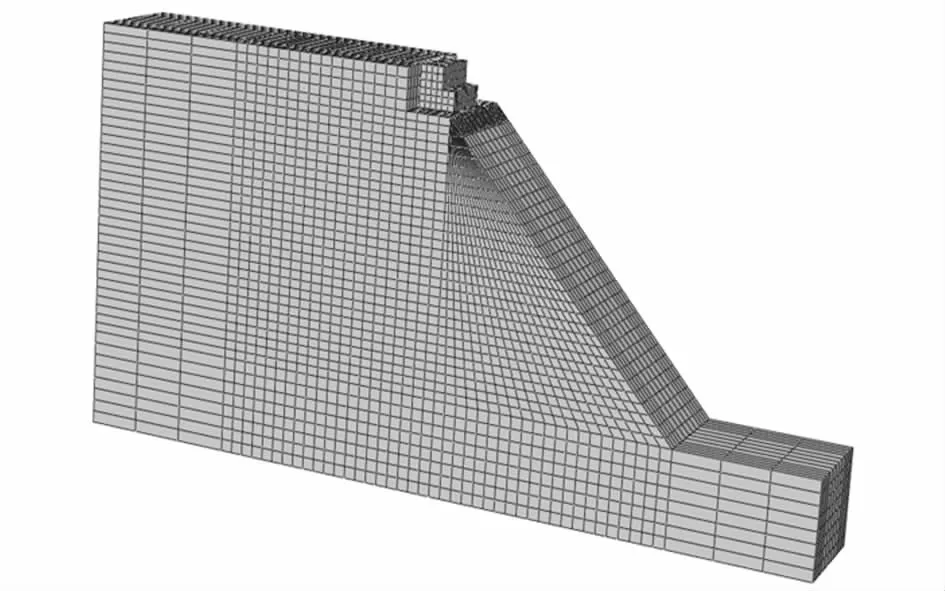
图3 有限元分析模型Fig.3 Finite element analysis model

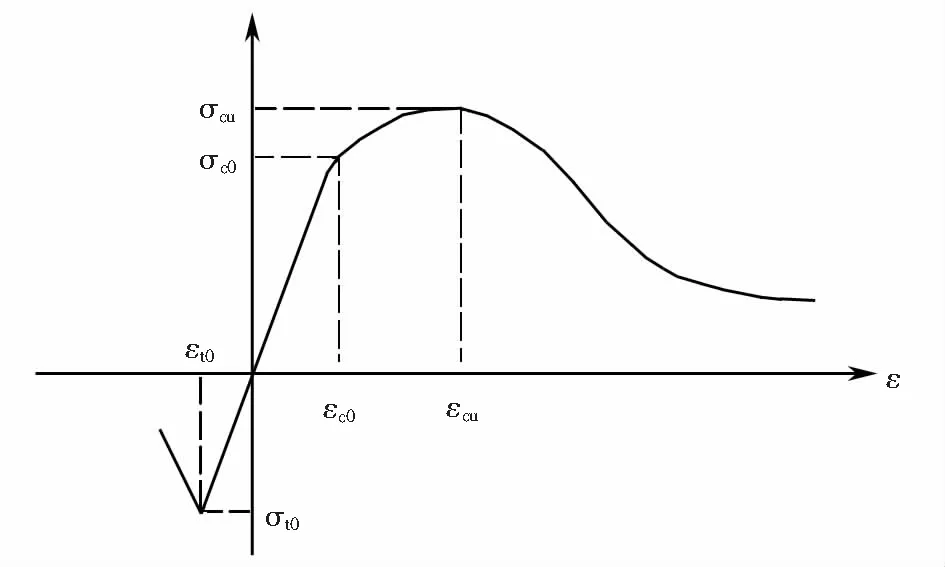
图4 混凝土应力-应变关系Fig.4 Stress-strain relationship in concrete

表1 土体参数

2.2 边界条件及加载历程

桥台、桩基与土体间采用面面接触，混凝土面为主接触面，土面为从属面.主面与从面间的切向行为采用罚函数模拟，摩擦系数取0.2.模型沿纵向(线路方向)两侧及横向两侧均约束水平位移，底部约束水平及竖向位移.模型的加载程序按位移控制(以河沟侧为正，路堤侧为负)，每次循环往复一次，按50 mm级差加载至600 mm.加载历程如图5所示.模型中将桥跨结构及二期恒载产生的竖向力施加于桥台顶部.

2.3 分析区域及网格划分

模型分析区域的确定及网格划分的精度是数值模拟的关键，合理的分析区域及网格划分既能使计算结果真实反映桥台的受力特征，又能最大限度的减小运算成本.通过有限元模型的对比，本算例中台后填土沿路堤侧取60 m,坡脚前方取25 m，坡脚以下取15 m.为提高运算效率，台背后方5H(H为桥台高度)及边坡范围内按0.25 m网格加密，其余范围按2 m划分.

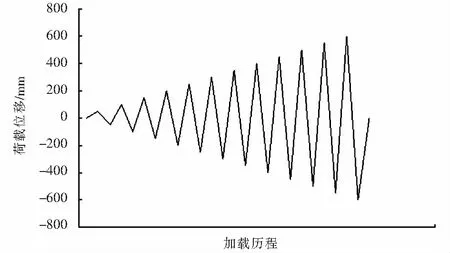
图5 加载历程Fig.5 Loading process

3 数值模拟计算结果

为研究有无边坡及边坡影响下不同桥台高度对桩基础桥台抗震性能的影响，设计了4种工况，不同工况下的模型参数如表2所列.对4种工况下桩基础桥台模型进行分析计算，通过分析获得了不同工况下模型的滞回曲线和骨架曲线.

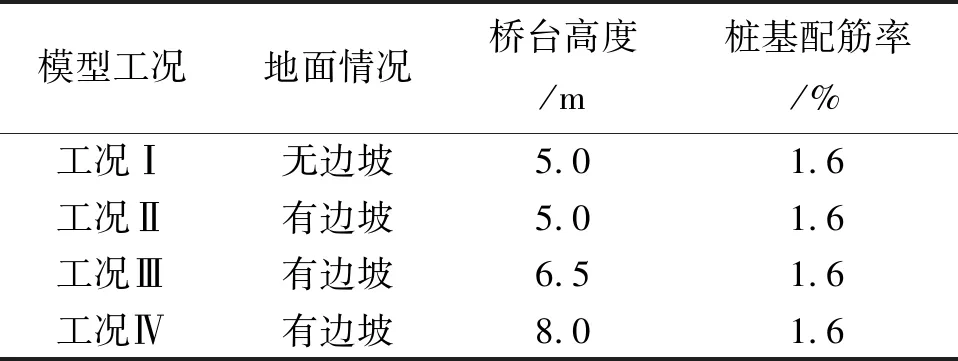
表2 模型工况

3.1 滞回曲线

为研究边坡对桩基桥台抗震性能的影响，通过工况Ⅰ和工况Ⅱ分别计算了桥台高度为5 m时无边坡和有边坡两种情况下桩基桥台的滞回曲线如图6所示.另外，通过工况Ⅱ～工况Ⅳ分别计算了边坡存在时不同桥台高度下桩基桥台的滞回曲线如图7所示.由图6～7可知，桩基桥台的滞回曲线呈明显的非对称性，路堤侧滞回曲线的捏缩较河沟侧严重，这说明桩基桥台河沟侧的耗能能力强于路堤侧.由图6可知，工况Ⅰ中河沟侧的滞回曲线较工况Ⅱ的饱满，路堤侧两者差别不明显，说明边坡的存在降低了桩基桥台河沟侧的耗能能力.由图7可知，随着桥台高度的增加，桩基桥台的滞回曲线捏缩愈加严重，这说明桥台高度的增加削弱了桩基桥台的耗能能力.

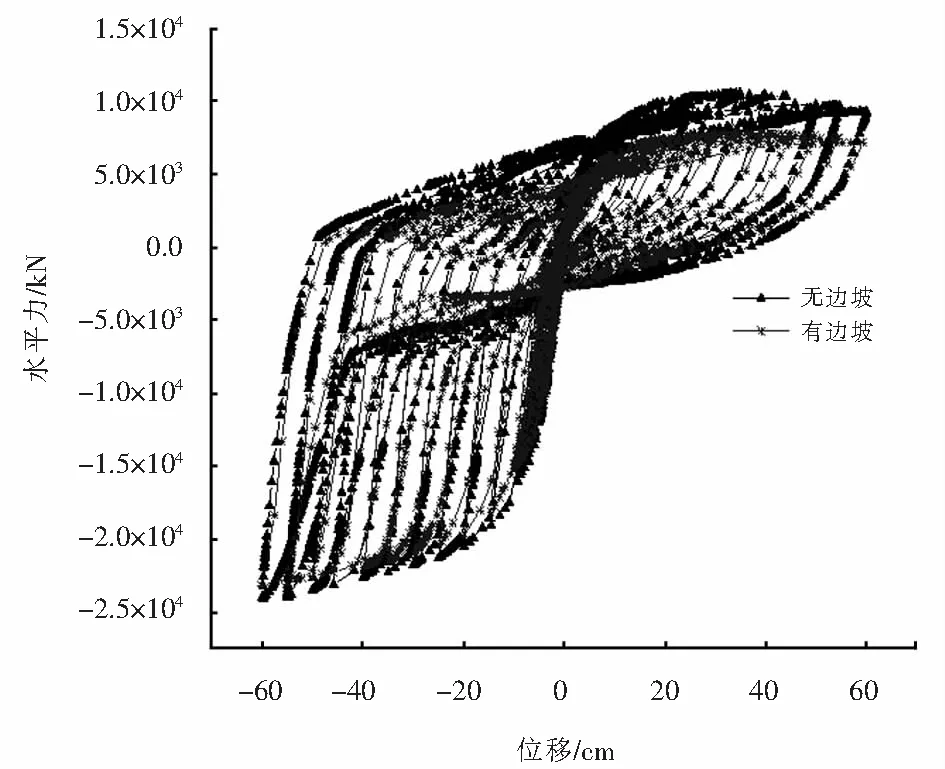
图6 有无边坡两种情况下桩基桥台滞回曲线对比Fig.6 Comparison of hysteresis curve of pile abutment with or without slope

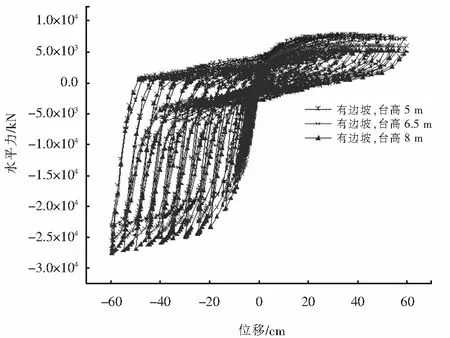
图7 不同桥台高度下桩基桥台滞回曲线对比Fig.7 Comparison of hysteresis curve of pile abutment under different abutment heights

3.2 骨架曲线

无边坡和有边坡两种工况下桩基桥台的骨架曲线如图8所示，由图8可以发现，桩基桥台河沟侧的骨架曲线可分为四个阶段：弹性阶段、塑性阶段、塑性硬化阶段和失效阶段.弹性阶段：桥台的荷载随位移线性增加；塑性阶段：随着位移的增加，荷载的增长速率变缓；塑性硬化阶段：随着位移的继续增大，桥台的承载力增长缓慢，骨架曲线表现出较长的平台；失效阶段：桥台的承载力随位移的增加而下降.需要说明的是由于台后填土的存在，桩基桥台路堤侧的骨架曲线没有出现失效阶段且路堤侧承载力明显高于河沟侧承载力.另外，边坡存在的情况下桩基桥台的河沟侧承载力低于无边坡的情况，有边坡时桥台的河沟侧承载力较无边坡时平均降低25.1%，这主要是由于边坡的存在削弱了土体对桩基础河沟侧的约束.有边坡和无边坡两种情况下桩基桥台的路堤侧承载力无明显差异，说明边坡对桩基桥台路堤侧承载力无显著影响.边坡存在情况下不同桥台高度的桩基桥台骨架曲线如图9所示，由图9可知，随着桥台高度的增加，桩基桥台河沟侧承载力降低而路堤侧承载力提高且河沟侧承载力的降低幅度较路堤侧承载力的增长幅度显著，例如，桥台高度由5 m增加到8 m时河沟侧承载力平均降低34%而路堤侧平均提高19.5%.

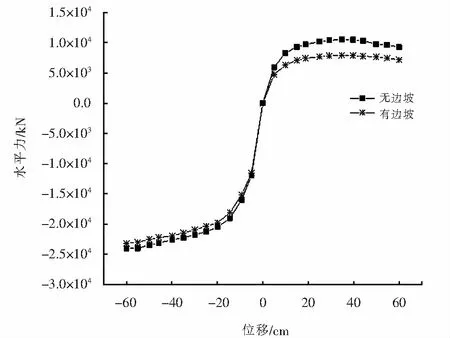
图8 有无边坡两种情况下桩基桥台骨架曲线对比Fig.8 Comparison of skeleton curve of pile abutment with or without slope

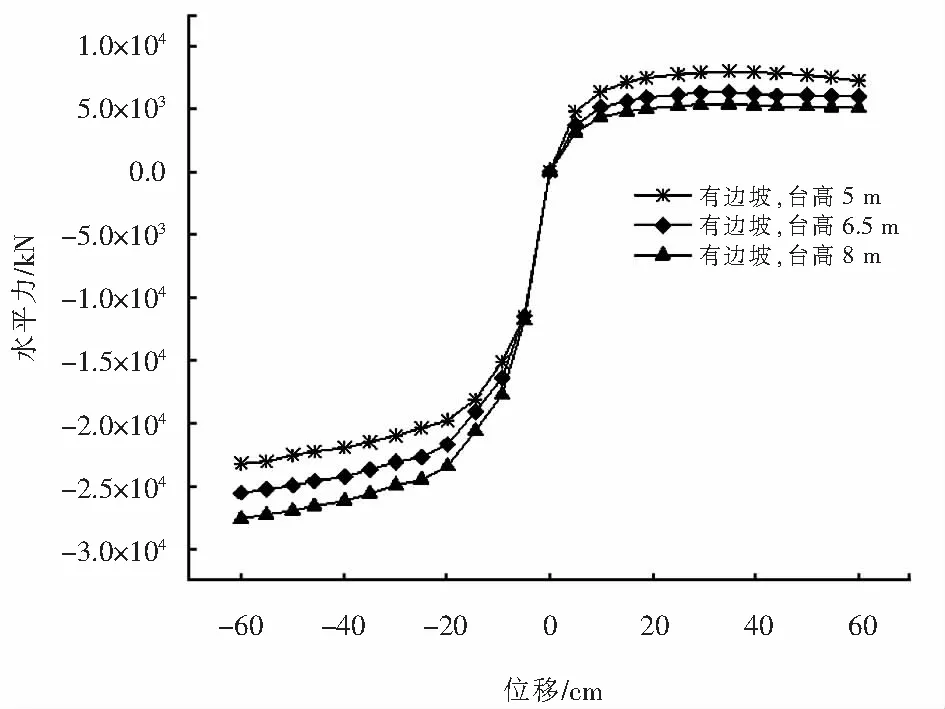
图9 不同桥台高度下桩基桥台骨架曲线对比Fig.9 Comparison of skeleton curve of pile abutment under different abutment heights

3.3 桩基位移

沿台后向台前编号，当位移荷载达到600 mm时，无边坡和有边坡两种情况下前排及后排桩沿桩深的纵向位移分布如图10～11所示(以台背高度为5 m的工况为例).

由图10可知桩基的纵向位移最大值出现在桩顶，前排桩的纵向最大位移大于后排桩，位移主要发生在桩顶以下8倍桩径范围内.位移曲线出现了两次反弯点，这主要是由于桥台除了产生水平位移外还发生了偏转.对比图10和图11可以发现有边坡时桩顶的纵向位移明显大于无边坡的情况，有边坡时前排桩桩顶的纵向位移较无边坡时增大79%，后排桩增大54%.这主要是由于边坡的存在削弱了土体对桩基的纵向约束.

图10 无边坡情况下桩基纵向位移Fig.10 Longitudinal displacement of pile foundation without slope

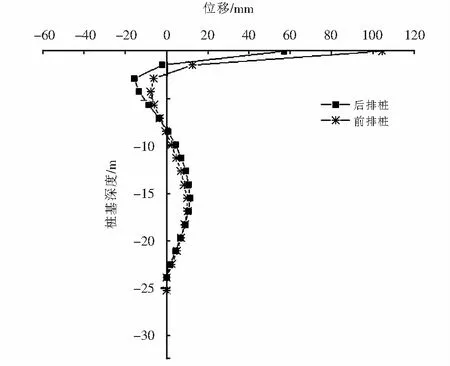
图11 有边坡情况下桩基纵向位移Fig.11 Longitudinal displacement of pile foundation with slope

4 抗震性能分析

4.1 耗能能力

等效粘滞阻尼系数ξeq是表征结构耗能能力的重要指标，如图12所示为经典的滞回环，ξeq可通过公式(1)计算得到.图12中SABCD为滞回环的面积，SOFD+SOBE为结构储存的弹性应变能.鉴于桥台的滞回曲线表现出明显的非对称性，因此按河沟侧和路堤侧分别计算桩基桥台的等效粘滞阻尼系数.工况Ⅰ～Ⅱ和工况Ⅱ～Ⅳ中桩基桥台的ξeq如图13～14所示.

(1)

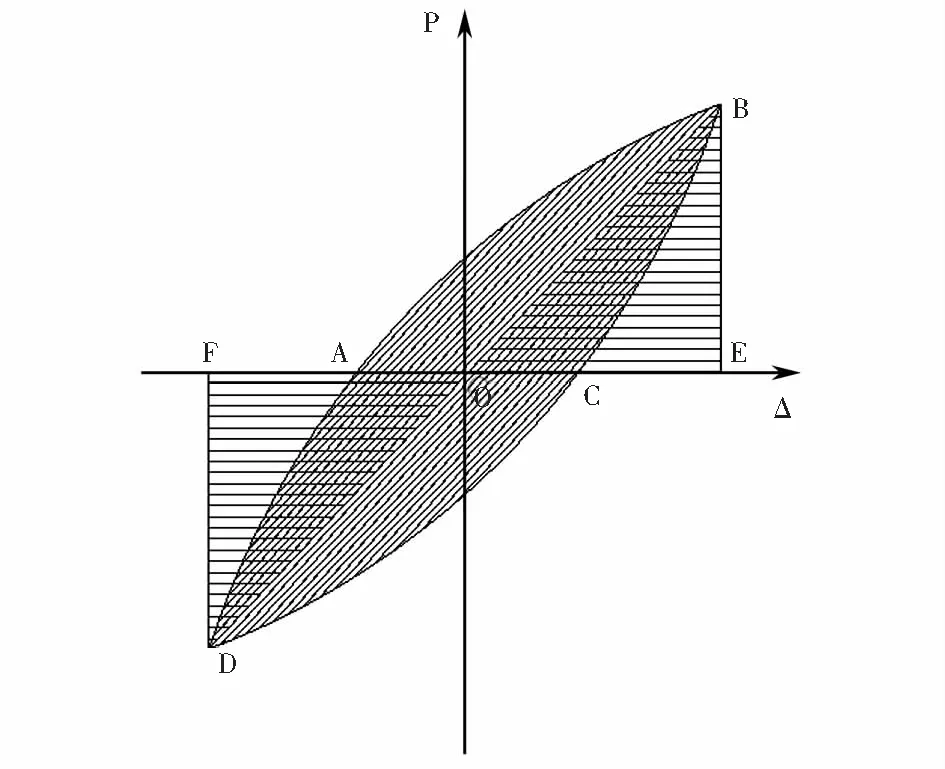
图12 经典滞回环Fig.12 Typical hysteretic loop

图13 边坡对等效粘滞阻尼系数的影响Fig.13 Effect of slope on equivalent viscous damping coefficient

由图13可知，边坡对桩基桥台的耗能能力存在影响，边坡使桥台的耗能能力降低，但河沟侧的降低程度明显强于路堤侧，这主要是由于边坡降低了土体对桩基尤其是靠边坡一侧桩基的约束.与无边坡情况相比，边坡使桩基桥台河沟侧的ξeq平均降低17.4%，路堤侧平均降低0.9%.由图14可以发现，随着桥台高度的增加，桩基桥台路堤侧的耗能能力降低，河沟侧的耗能能力变化不明显.另外，从总体来看尽管桩基桥台路堤侧的承载能力高于河沟侧，但路堤侧的耗能能力低于河沟侧，这是由于桥台路堤侧的耗能主要源于台背土体而河沟侧的耗能源于桩基.

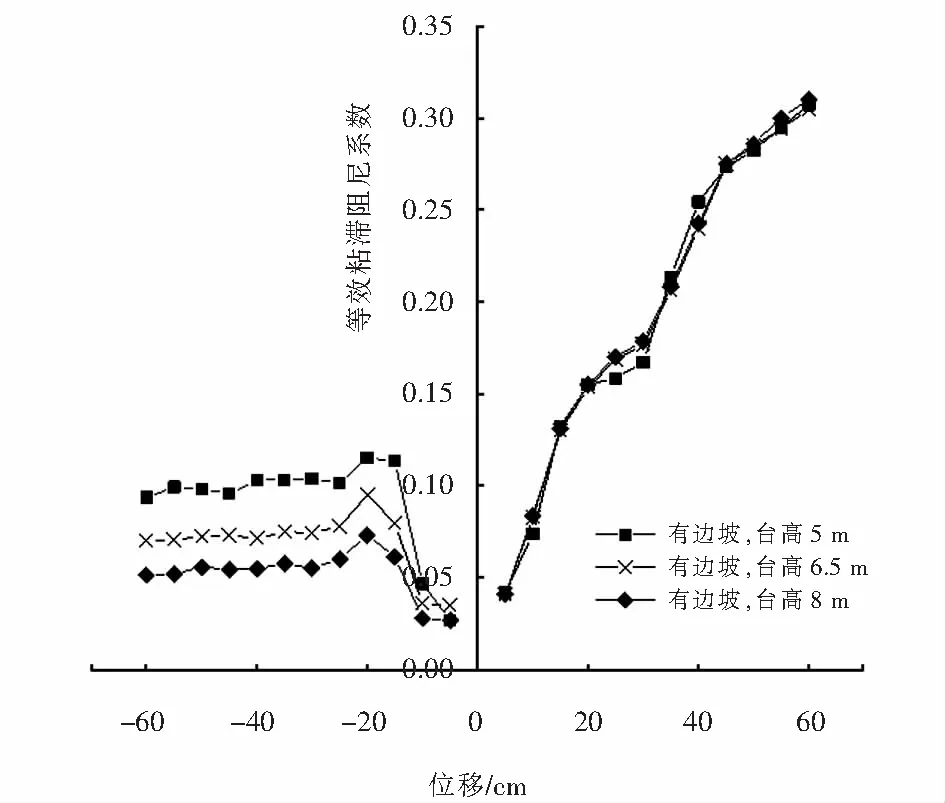
图14 桥台高度对等效粘滞阻尼系数的影响Fig.14 Influence of abutment height on equivalent viscous damping coefficient

4.2 刚度退化

为更直观的反映桩基桥台在循环荷载下的刚度变化情况，引入割线刚度的概念计算桩基桥台的刚度，各种工况下桩基桥台的刚度变化如图15～16所示，割线刚度采用公式(2)计算.

(2)

式中：Ki表示割线刚度；±Fi表示第i次循环荷载下的正、负最大荷载；±Δi为±Fi对应的位移.

由图15可知，边坡使桩基桥台河沟侧的刚度平均降低23.6%，但对路堤侧的刚度几乎没有影响.另外，由图15可知无边坡时桩基桥台的河沟侧刚度从初始割线刚度1 190.8 kN/cm逐渐减小至154.4 kN/cm，约退化为初始割线刚度的12.9%，而有边坡时桩基桥台的河沟侧刚度从初始割线刚度950 kN/cm逐渐减小至119.5 kN/cm，约退化为初始割线刚度的12.6%.这说明边坡整体上降低了桩基桥台河沟侧的刚度，但对结构刚度退化的影响并不明显.

由图16可以发现，边坡存在的情况下，随着桥台高度的增加，桩基桥台河沟侧的刚度减小而路堤侧的刚度增大，例如，当桥台高度由5 m增至8 m时，桩基桥台河沟侧刚度平均降低32.6%，而路堤侧刚度平均增加17%.另外，随着桥台高度由5 m增至8 m，桩基桥台河沟侧刚度平均退化约87%而路堤侧刚度平均退化约82.1%，说明边坡存在时桥台高度对结构河沟侧刚度退化的影响较路堤侧更加显著.

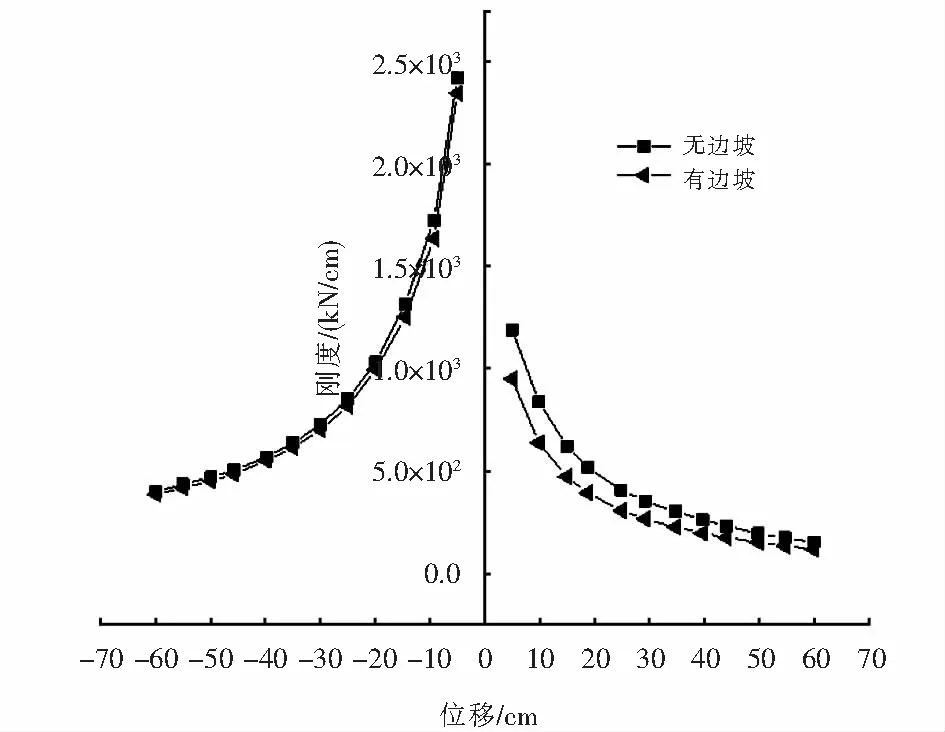
图15 有无边坡两种情况下桩基桥台刚度退化对比Fig.15 Comparison of stiffness degeneration of pile abutment with or without slope

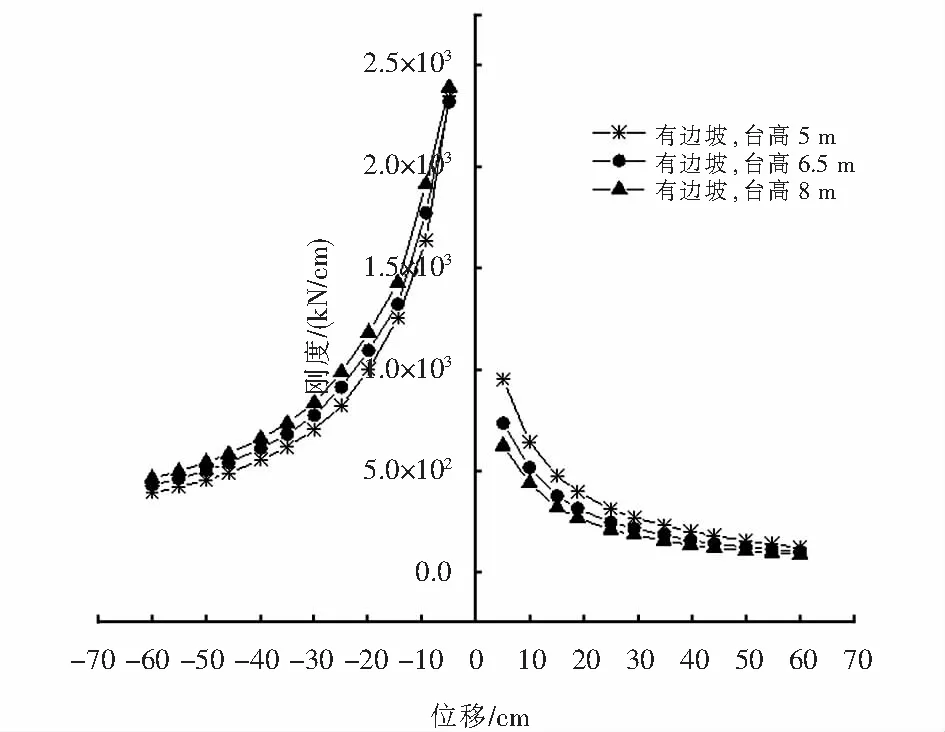
图16 不同桥台高度下桩基桥台刚度退化对比Fig.16 Comparison of stiffness degeneration of pile abutment under different abutment heights

5 结论

通过分析边坡对铁路桥台抗震性能的影响，得到以下结论：

1) 由于台背土的参与，桩基础桥台的滞回曲线呈明显的非对称性，桥台路堤侧的承载力高于河沟侧.

2) 边坡对桩基桥台的承载能力、耗能能力及刚度存在较大影响.与无边坡情况相比，边坡导致桩基桥台河沟侧的承载力平均降低25.1%，等效粘滞阻尼系数平均降低17.4%.边坡的存在整体上降低了桩基桥台河沟侧的刚度.

3) 桥台高度对桩基桥台的承载能力、耗能能力及刚度退化也存在较大影响.台背高度导致桩基桥台河沟侧承载力降低而路堤侧承载力提高，河沟侧刚度减小而路堤侧刚度增大.随着台背高度的增加，桩基桥台路堤侧耗能能力降低而河沟侧耗能能力变化不明显.

4) 由于边坡的存在对桩基桥台的承载能力、耗能能力及刚度均有较大影响，因此，边坡地区桩基础桥台抗震设计时应考虑边坡的影响并采取必要的构造措施.