Q420qD钢材应力腐蚀特征试验研究
2022-02-23张素梅陈广锐李爱东郭现钊郭兰慧
张素梅,陈广锐,李爱东,郭现钊,张 磊,郭兰慧
(1. 哈尔滨工业大学(深圳) 土木与环境工程学院,广东 深圳 518055; 2. 中国铁路设计集团有限公司,天津 300308; 3. 哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150010)
0 引 言
随着中国土木工程和基础设施建设的高速发展,对高性能钢材的需求日益增加。近10年来,具有高强度、高韧性等优良性能的Q420qD钢成为交通土建建设中非常重要的钢种,受到投资方和设计人员的青睐,如已建成的港珠澳大桥采用了Q420qD钢制作钢箱梁,以及即将建设的澳门澳氹第4条跨海大桥拟采用Q420qD钢等。随着Q420qD钢越来越多的应用于海洋、工业大气或地下水侵蚀等复杂环境中,由此导致的钢材腐蚀将造成结构构件截面损失、性能退化和耐久性降低等问题,使得钢结构在服役期限内的腐蚀问题成为影响其全寿命耐久性设计的重要因素。同时,钢结构在正常使用阶段由于承受荷载而带应力工作,特别是地下结构还受到周围环境中杂散电流的影响,这些不利因素将进一步加剧钢结构的腐蚀。
根据材料的腐蚀形态可以将钢材的腐蚀划分为全面腐蚀和局部腐蚀,局部腐蚀又包括点蚀、电偶腐蚀、晶间腐蚀等。一般情况下,局部腐蚀的危险性远大于全面腐蚀。当环境因素和应力共同作用时,钢材就会发生应力腐蚀。有研究表明[1],应力会加快腐蚀速率,削弱钢结构截面,因此应力腐蚀危害性更大。全面腐蚀会造成钢结构截面面积减小,承载能力下降[2-4]。局部腐蚀会引起局部蚀坑处的应力集中[5-6],降低钢结构的延性[7-8],同时局部腐蚀还可以造成截面的不对称、荷载的偏心变化、疲劳性能的降低[9]等。国内外诸多学者在钢材腐蚀方面做了大量的有益探索。徐小连等[10]对Q420qD钢材和F500L-Z普钢进行了中性盐雾试验和电化学测试,发现Q420qD钢材的耐腐蚀性明显优于F500L-Z普钢;盛杰[11]研究了在地下环境中Q235钢材应力腐蚀特征,并发现腐蚀试件表面形貌的分形维数在不同荷载比下随着腐蚀时间的增加均呈现先增后减的规律。李安邦等[12]利用盒宽变换法计算了中性盐雾加速腐蚀环境中Q235B钢板腐蚀表面分形维数,并研究其随腐蚀龄期、质量损失率以及表面粗糙度的变化规律。目前,对钢材腐蚀的研究主要针对Q235[11]、Q355[13-14]等钢种,且多未考虑应力腐蚀,而对于Q420qD钢材的腐蚀研究较少,且对Q420qD应力腐蚀研究还未见报道。
研究钢材腐蚀特征是进一步研究其对钢材力学性能劣化程度的基础。复杂的腐蚀环境和钢材不同的化学成分、组织结构、表面状态以及构件自身的受力状态都将影响材料表面腐蚀形貌特征,进而对其力学性能产生影响。因此,本文针对Q420qD钢材在低应力工况下的腐蚀特征进行试验研究,采用形貌扫描方法获得钢材表面蚀坑的重要参数,利用差分盒计数法计算试件表面分形维数并研究其随腐蚀时间和质量损失率的变化规律。本文的工作对进一步完善中国钢结构全寿命耐久性设计、既有结构鉴定加固与寿命预测等具有重要意义。
1 腐蚀试验
1.1 试件设计与应力加载方案
本次试验腐蚀试件采用Q420qD钢材制作,共制作了60个腐蚀试件,其中有应力和无应力腐蚀试件各30个。根据《金属材料拉伸试验第1部分:室温试验方法》(GB/T 228.1—2010)和《金属拉伸试验试样》(GB 6397-86)采用线切割制作而成。钢材标准拉伸试件由夹持段、过渡段和试验段组成,总长均为200 mm,厚6 mm,具体尺寸见图1(a)。应力腐蚀试件两端开设圆孔,孔径为14 mm,以便对试件施加应力,试件尺寸见图1(b)。

图1 腐蚀试件(单位:mm)Fig.1 Corrosion Specimens (Unit:mm)
对未腐蚀钢材进行材性试验,分别测试了钢材的弹性模量、屈服强度、极限强度、伸长率和泊松比,试验测得的弹性模量在198~207 GPa之间,屈服强度在435~454 MPa之间,极限强度在541~556 MPa之间,其他具体测试结果见表1。

表1 钢材力学性能Table 1 Mechanical Properties of Steel
构件的工作应力加载通过加力环实现。加力环是一种受力自相平衡的结构,每个加力环可容纳3个试件同时承受工作荷载。试件与加力环之间采用连接件和8.8级高强螺栓连接,加载装置示意图见图2。

图2 加载装置示意图Fig.2 Sketch of Loading Device
采用高精度扭力扳手对试件施加预拉力,扭力扳手根据公式(1)对螺栓施加扭矩,由螺栓中产生的预紧力对试件施加拉力,取应力腐蚀试件所受荷载为其屈服荷载的0.3倍。在正式加载前先通过应变片校核预紧力与拧紧力矩是否满足公式(1),确定拧紧力矩系数。在一组3个试件上粘贴应变片,根据采集的应变数值计算钢材所受荷载,并将该力与屈服荷载的0.3倍进行比较,从而确定拧紧力矩系数K为0.20,符合文献[11]中表4-2规定的取值范围0.18~0.21。
Mt=KP0d
(1)
式中:Mt为拧紧力矩;P0为预紧力;d为螺母公称直径。
1.2 试验过程
1.2.1 腐蚀方法
钢材腐蚀试验方法主要分为2种:一种为自然环境长期暴露腐蚀试验,另一种为实验室加速腐蚀试验。自然环境暴露腐蚀试验具有试验结果真实可靠的优点,但存在试验周期长和管理难度大等缺点。实验室加速腐蚀试验具有试验周期短和腐蚀结果较好的优点,其中通电加速腐蚀试验具有定量控制金属腐蚀质量和腐蚀速率的优点[15]。因此,本次采用实验室通电加速腐蚀的方法进行钢材腐蚀。
腐蚀试验分为有应力腐蚀试验和无应力腐蚀试验2类,每类各有10组试件,每组有条件相同的3个试件。每类试件的目标腐蚀率为3%~30%,中间按照等间隔腐蚀率设置。试验系统由LODESTAR LPS605D恒流源、有机玻璃水槽、Q420qD钢材试件、铜箔、导线及质量分数为5%的NaCl溶液等组成。试验采用部分浸入的方式进行电化学加速腐蚀试验,腐蚀部位为试件平行段。试验中试件放入卡槽内,并用硅胶进行密封,防止NaCl溶液漏出。根据文献[16],腐蚀电流密度取2 mA·cm-2,电化学加速腐蚀试验系统如图3所示。

图3 加速腐蚀试验系统Fig.3 Accelerated Corrosion Test System
根据电解原理,图3中试件作为阳极连接电源正极,发生氧化反应进而溶解,铜片作为阴极连接电源负极,铜片表面产生氢气。根据目标腐蚀率可计算出理论腐蚀质量,继而可利用法拉第电解定律推算出在一定电流下的理论通电时间,见式(2)。通过调整电流,即可在较短时间内实现腐蚀。
(2)
式中:δ为腐蚀损失质量;M为铁的摩尔质量;I为腐蚀电流;T为通电时间;F为法拉第常量,取96 500 C·mol-1;Z为反应电极化学价,取2。
在开始腐蚀试验前需对本试验系统进行验证。取3个试件进行腐蚀试验,分别称重并记录下原始质量,按照本文试验方法通电加速腐蚀后,腐蚀试件根据《金属和合金的腐蚀 腐蚀试样上腐蚀产物的清除》(GB/T 16545—2015)清除试件表面的腐蚀产物,分别称重并记录下腐蚀后质量,由此可计算出损失质量,并将该质量与理论损失质量进行比较,比较结果表明数据接近,离散程度小,说明试验方案可行。正式腐蚀试验中,电流为0.05 A,目标腐蚀率为3%时的通电时间为22 h,其他组的腐蚀时间以此类推,则目标腐蚀率为30%的第10组试件通电时间为220 h。为了减少试件并联带来的误差,试验中每个试件连接一台电源。无应力试件与其相应组别的有应力试件同时腐蚀,待通电完成后同时关闭电源,取出腐蚀试件进行除锈处理。
1.2.2 形貌扫描
腐蚀后试件采用德国GOM公司生产的ATOS三维扫描仪对试件表面进行形貌扫描,见图4。

图4 ATOS三维扫描仪Fig.4 ATOS 3D Scanner
试验中从每一组3个试件中选择形貌发展具有典型特征的1个试件进行扫描,无应力组和有应力组各对10个试件进行扫描,一共扫描20个试件。由于试件是金属制品,扫描前首先对试件的扫描面喷涂显像剂,再放于工作台上进行扫描,从而获取表面三维形貌数据。扫描完成后,利用系统配套的软件GOM Inspect进行拟合处理,从而得到表面腐蚀形貌,测量精度为0.01 mm,并且采用佳能单反相机对所有试件表面进行照片采集,从而利用差分盒计数法计算腐蚀试件表面分形维数。
2 试验结果及分析
2.1 腐蚀速率
评价金属腐蚀损伤程度的指标有质量损失率、截面损失率、表面粗糙度、分形维数等。质量损失率η是其中一个基本且重要的指标,其定义见式(3)。
(3)
式中:m0为试件初始质量;mc为试件除锈后质量。
对所有腐蚀试件除锈后进行称重,计算其质量损失率,并绘制有应力和无应力试件质量损失率η与腐蚀时间t散点图,如图5所示。由图5可知,荷载比为0.3的有应力和无应力工况下试件的质量损失率均随着腐蚀时间的增长而呈现非线性递增关系。在通电时间为132 h之前,有应力试件的质量损失率明显高于无应力试件,有应力和无应力试件的腐蚀速率呈明显线性增长。分别对132 h之前的有应力和无应力数据进行线性拟合,拟合结果见式(4)、(5),发现有应力试件的腐蚀速率是无应力试件的1.15倍,但随着腐蚀时间的增加,试件表面腐蚀产物逐渐堆积,表面锈层逐渐变厚,阻碍了钢材表面与溶液、氧气等发生化学反应,所以导致腐蚀速率变慢,有应力和无应力试件腐蚀速率无明显区别。

图5 质量损失率-腐蚀时间关系Fig.5 Relation of Mass Loss Rate-corrosion Age
无应力组
η=1.43×10-3t,R2=0.986 4
(4)
有应力组
η=1.65×10-3t,R2=0.972 9
(5)
选择对数函数作为目标函数对图5中的有应力和无应力组的数据进行非线性拟合,拟合结果见式(6)、(7)。可以看出,确定系数R2均非常接近1,说明质量损失率与腐蚀时间较好地符合对数函数关系。
无应力组
η=ln(1.56×10-3t+1),R2=0.994 3
(6)
有应力组
η=ln(1.67×10-3t+1),R2=0.978 0
(7)
通过对比有应力和无应力试件的拟合曲线,可以发现在相同腐蚀环境下,有应力试件的腐蚀速率要略快于无应力试件,说明应力的存在会加速腐蚀速率。
2.2 表面形貌发展规律
腐蚀试件的表面形貌扫描数据经过GOM Inspect软件处理后,可以较直观地看出表面腐蚀深度的变化。无应力和有应力试件组各挑选5张具有代表性的形貌发展图片,见图6与图7。
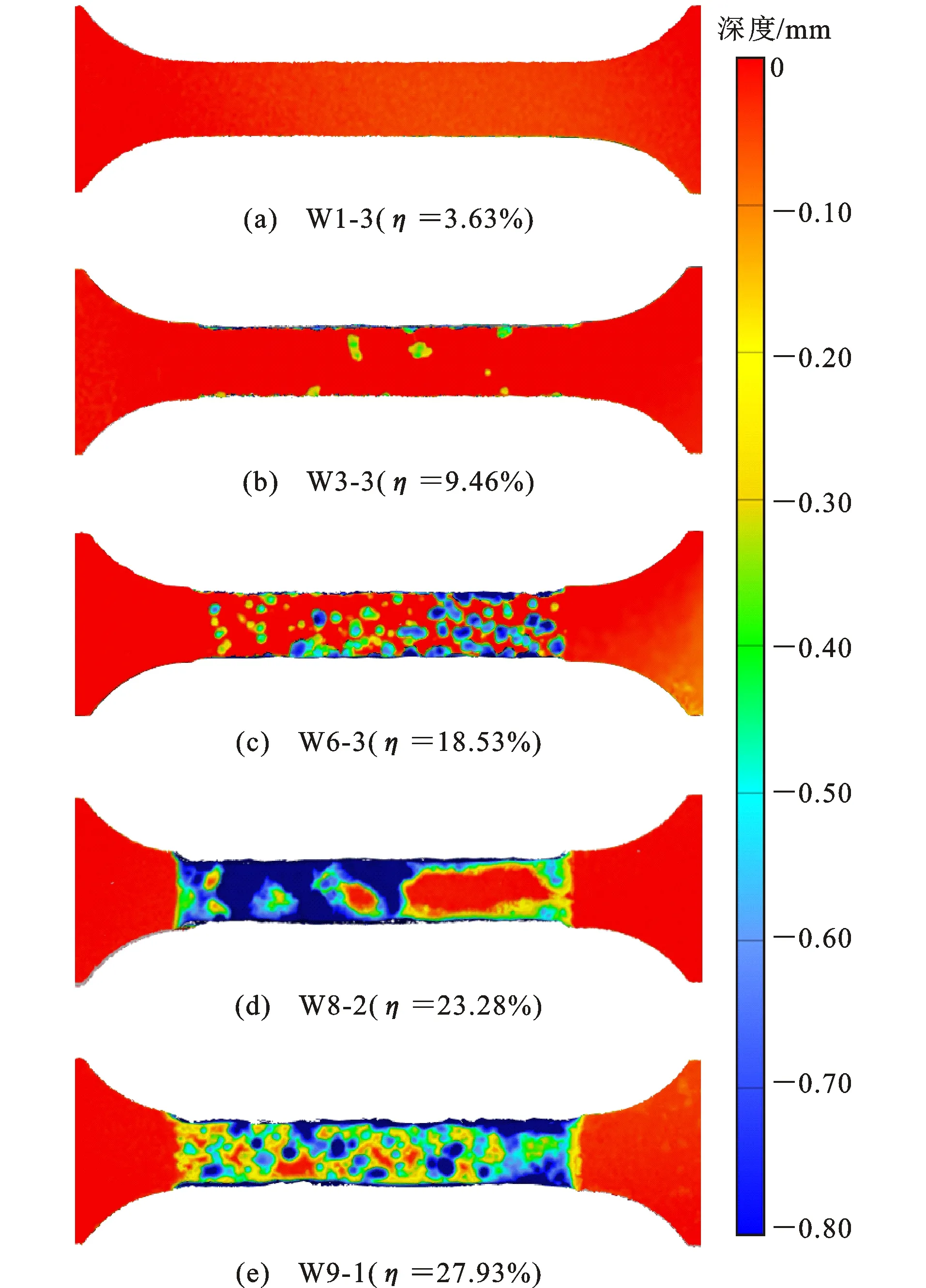
图6 无应力试件腐蚀形貌发展Fig.6 Corrosion Morphology Developments of Unstressed Specimens

图7 有应力试件腐蚀形貌发展Fig.7 Corrosion Morphology Developments of Stressed Specimens
根据文献[11]中对腐蚀形貌发展的3个时期划分,从图6和图7中可知,2种工况下试件的腐蚀形貌发展都经历了腐蚀初期、中期和后期。初期以局部腐蚀为主,表面部分区域发生腐蚀,即试件部分表面出现蚀坑,此时腐蚀形态以点蚀为主。随着腐蚀进程的推进,钢材表面腐蚀区域不断扩大,蚀坑数量增加,遍布在钢材表面,蚀坑继续向深度方向发展,并且相邻蚀坑有相互连接的趋势。腐蚀后期,大部分蚀坑连成一片,试件表面腐蚀深度差异变小,此时主要以均匀腐蚀为主。
通过图6与图7中有应力和无应力组试件腐蚀形貌的对比可知,相同腐蚀环境下,应力的存在会加速表面腐蚀形貌的发展。原因是应力的存在会显著提高钢材表面的腐蚀活性,加快钢材腐蚀速率[1]。第1组第3个无应力试件W1-3通电时间为22 h,质量损失率为3.63%,腐蚀主要发生于试件的侧面。由于试件侧面由线切割加工而成,侧面的粗糙度明显高于钢材表面,侧面的钝化膜厚度不均,容易遭受腐蚀,而其表面几乎未出现蚀坑。通电时间同样为22 h的第1组第3个有应力试件Y1-3质量损失率达到了4.65%,表面已经出现少许蚀坑。
随着腐蚀继续发展,通电时间为66 h时,第3组第3个无应力试件W3-3质量损失率为9.46%,表面出现蚀坑,数量少但蚀坑直径大,蚀坑之间距离较远,蚀坑最大深度达到0.4 mm左右,而第3组第3个有应力试件Y3-3质量损失率达到了12.41%,表面出现大量蚀坑但直径很小,蚀坑之间距离较近,蚀坑深度普遍在0.2 mm左右。通电时间为132 h时,第6组第3个无应力试件W6-3质量损失率为18.53%,表面出现大量直径大、深度深的蚀坑,但并未明显相连,而质量损失率为19.65%的有应力试件Y6-3大部分蚀坑虽然深度浅但已经连成一片。通电时间分别为176 h和198 h时,第8组和第9组的有应力和无应力试件表面蚀坑均已连成一片,腐蚀形态以均匀腐蚀为主。由以上分析可知,荷载比为0.3的有应力腐蚀试件的表面形貌发展要快于相同腐蚀环境下的无应力腐蚀试件,而且无论是否存在应力,腐蚀形态最终都以均匀腐蚀为主。
2.3 表面分形维数
2.3.1 分形维数计算原理
1967年Mandelbrot在解决“英国海岸线长度”问题时提出了维数不一定是正整数也可以是分数的观点,从此分形理论便作为一个非线性新兴学科得到快速发展并成为处理自然界零碎和复杂现象的有力工具。目前分形维数有多种计算方法,如盒计数法、分规法、面积-周长法、均方根法等。由于差分盒维数法计算精度较高且适合计算灰度图像[11],本文采用差分盒维数法计算钢材表面腐蚀形貌的分形维数。计算原理[17]为:假设图像大小为P×P像素,用边长为s的小正方形进行分割(1 nr(i)=l-k+1 (8) 将所有格子中的nr求和,得 (9) 式中:N为图像每边的格子数,N=r。 取多个不同的s值,可得到多个Nr值,利用最小二乘法拟合lg(Nr)-lg(r),则所得拟合曲线的斜率就是该图像的分形维数D。具体计算过程通过编写程序实现。 2.3.2 分形维数变化规律 为验证钢材表面腐蚀形貌是否具备分形特征,分别取无应力组和有应力组各1个试件作为典型试件,做出lg(Nr)-lg(r)的散点图并进行线性拟合,见图8,拟合公式见式(10)和式(11)。可以发现,无论是应力腐蚀试件还是无应力腐蚀试件,lg(Nr)与lg(r)存在显著的线性相关性,因此可以对钢材表面腐蚀形貌进行分行维数计算。 图8 lg(Nr)-lg(r)拟合结果Fig.8 lg(Nr)-lg(r) Fitting Results 无应力组 y=2.208 1x+0.200 3,R2=0.996 7 (10) 有应力组 y=2.381 1x+0.480 2,R2=0.994 8 (11) 本试验计算了所有腐蚀试件表面形貌的分形维数,作出分形维数与质量损失率和腐蚀时间的散点图,见图9。 图9 分形维数变化规律Fig.9 Variation Laws of Fractal Dimension 为了便于观察分形维数的变化规律,计算出每一组3个试件表面分形维数的平均值,将其作为每一组分形维数的代表值。有应力组(Y)和无应力组(W)的平均值随着质量损失率和腐蚀时间的变化规律如图10所示。 图10 分形维数平均值变化规律Fig.10 Variation Laws of Average Fractal Dimension 从图9与图10可以看出,在通电66 h内,无应力组的分形维数在腐蚀初期(质量损失率小于9%)不断增大,超过初期后分形维数出现减小—增大—减小的上下波动现象。有应力组试件由于表面形貌发展较快,腐蚀初期较短,当通电44 h质量损失率超过8%时,分形维数便进入先减小再增大的上下波动过程。产生上述现象的原因可能是:腐蚀初期的腐蚀形态以点蚀为主,局部出现少量蚀坑,表面粗糙程度迅速增加,分形维数迅速增大;随着腐蚀时间增加,钢材表面出现大量尺寸较小蚀坑,并逐渐连成片状,出现大面积均匀腐蚀,表面凹凸不平程度有所减缓,分形维数出现一定程度降低;后期随着腐蚀产物的聚集,锈层逐渐变厚,在一定程度上阻碍了溶液与钢材表面的接触;若蚀坑向深度方向发展受阻,则蚀坑会优先向宽度方向发展,腐蚀形态会由点蚀向均匀腐蚀转变,表面凹凸不平程度也在一定范围内上下波动,所以分形维数呈现周期性上下波动的规律。 从图9可以看出,在相同腐蚀环境下,有应力试件的分形维数往往大于无应力试件,说明有应力试件表面凹凸不平程度更严重,表面粗糙程度更大。通过对图10(a)中有应力和无应力试件在腐蚀初期分形维数发展速率方面进行对比,可以发现无应力试件在分形维数初期发展速率呈现先快后慢再快的规律,而有应力试件在腐蚀初期的分形维数呈现明显的线性增长规律,且发展速率明显高于无应力试件。原因可能是应力的存在加速了钢材的腐蚀,有应力试件在相同腐蚀时间下质量损失更大,表面腐蚀形貌发展更快,表面产生大量蚀坑并且蚀坑之间距离很小,容易相互连接,从而更快进入全面腐蚀。无应力试件由于腐蚀速率较低,表面形貌发展相对较慢,表面蚀坑数量随着腐蚀时间的增长逐渐增多,蚀坑相距由远及近,大多数蚀坑经过充分发展后才相互连接,随后钢材表面进入全面腐蚀,此时钢材表面腐蚀深度变化趋于平缓。 2.4.1 蚀坑深度分布规律 局部腐蚀主要以点蚀为主,钢材表面的蚀坑形状及尺寸常常引起不同程度的应力集中。目前,已有学者对管道[18]、H型钢[8,11,19]等表面的腐蚀深度分布规律做了大量研究,发现腐蚀钢材表面腐蚀深度在不同情况下服从正态分布、对数正态分布、Gumbel分布和双参数威布尔分布等。本节将对Q420qD钢材表面单坑腐蚀深度分布规律进行探索。腐蚀试件扫描后通过GOM Inspect软件中距离测量和表面偏差标注功能可以实现对表面蚀坑尺寸的测量。本试验对经过扫描的10个无应力试件和10个有应力试件进行表面蚀坑的统计。由于蚀坑相连后形状更加不规则,难以准确测量其直径和深度,所以只对未与其他蚀坑相连的单个蚀坑进行尺寸统计。腐蚀初期,表面主要发生点蚀,蚀坑数量稀少;腐蚀后期,试件表面主要以均匀腐蚀为主,单个蚀坑数量也较少。因此,本文选用表面出现大量单个蚀坑但大部分未与相邻蚀坑相连的2个试件进行深度分布规律分析。无应力试件选择第6组第2个试件W6-2,有应力试件选择第2组第1个试件Y2-1。采用ORIGIN2018软件对测量的单坑腐蚀深度数据进行分析并绘制频率分布直方图,见图11。 图11 蚀坑深度分布规律Fig.11 Distribution Principles of Pit Depths 根据文献[19]对本文的单坑腐蚀深度分布规律进行正态分布检验,首先需将蚀坑深度的正态分布函数线性变换为标准正态分布函数,再根据式(12)对标准正态随机变量z与正态随机变量腐蚀深度tc进行线性拟合。 (12) 式中:μ和σ分别为tc的均值和标准差。 由式(12)可得,tc与z之间存在显著线性关系。假设腐蚀深度服从正态分布,利用ORIGIN2018软件对z与tc进行最小二乘法拟合,得到: 无应力组W6-2 z=4.067 2tc-2.026 9,R2=0.972 0 (13) 有应力组Y2-1 z=22.629tc-3.488 2,R2=0.962 2 (14) 拟合公式中的确定系数R2都高于0.96,说明腐蚀深度较好地服从正态分布。由此可得到无应力试件W6-2与有应力试件Y2-1的概率密度函数和概率分布函数。 (1)无应力组W6-2 正态分布的概率密度函数为 (15) 分布函数为 (16) (2)有应力组Y2-1 正态分布的概率密度函数为 (17) 分布函数为 (18) 2.4.2 蚀坑的形态与径深比 国内外众多学者对蚀坑形态与径深比时变模型进行了深度研究,蚀坑的几何形状和径深比等几何参数是建立合理、全面的点蚀模型的重要依据,对准确进行相关有限元模拟具有重要意义。目前,被简化的蚀坑形态有圆柱体坑、半球形坑、球冠坑和圆锥坑等[21]。本文通过腐蚀试件扫描结果观察得到蚀坑近似呈球冠状的结论。绘制蚀坑直径-深度的散点图以及径深比随质量损失率的变化规律图,分别见图12和图13。 图12 蚀坑直径-深度关系Fig.12 Relationship Between Pit Diameter and Depth 图13 径深比与质量损失率关系Fig.13 Relationship Between Diameter to Depth Ratio and Mass Loss Rate 从图12可看出,蚀坑的径深比变化范围为2~8。其中无应力组的蚀坑数据较为离散且有一部分蚀坑直径和深度数值较大,而有应力组蚀坑数据较为集中且直径和深度较小。原因可能是应力加速了钢材的腐蚀,有应力试件表面蚀坑数量多,且蚀坑间距较小,更倾向于连成片状,所以蚀坑在直径和深度较小时就开始相互融合;无应力试件钢材表面蚀坑数量少,蚀坑相距较远,随着腐蚀时间的增加,蚀坑数量逐渐增多,导致一部分相邻蚀坑间距由大变小,逐渐相连,还有一部分蚀坑经过充分发展后,在蚀坑直径和深度达到一定值时才与相邻蚀坑连接,所以造成上述现象。 从图13可以看出,纵使有部分蚀坑径深比达到8或8以上,但在质量损失率大于7%左右后试件蚀坑的径深比有所降低,基本稳定在2~6,平均值在4附近波动,表明蚀坑趋于深窄。 (1)在相同腐蚀环境下,有应力和无应力试件的质量损失率随腐蚀时间均呈非线性单调递增关系,且有应力试件的腐蚀速率略快于无应力试件。通电时间在132 h以内即目标质量损失率在18%以内时,有应力和无应力试件腐蚀速率较快,质量损失率随腐蚀时间呈明显的线性增长关系,有应力试件腐蚀速率约为无应力试件的1.15倍,随着腐蚀时间的增加,后期腐蚀速率趋于平缓,有应力和无应力试件腐蚀速率无明显差别。 (2)应力腐蚀试件的表面形貌发展要快于相同腐蚀环境下的无应力腐蚀试件。有应力试件表面的蚀坑数量多,蚀坑间距小,更容易相互连接形成片状,腐蚀形态更容易由点蚀转变为均匀腐蚀。无应力试件表面形貌发展较慢,蚀坑数量随着腐蚀时间增长逐渐增多,蚀坑间距由远及近,腐蚀形态逐渐由点蚀转为均匀腐蚀。无论是否存在应力,试件的腐蚀形态最终都以均匀腐蚀为主。 (3)有应力和无应力试件的分形维数变化规律相似,都在腐蚀初期迅速增大,之后出现减小—增大—减小的周期性上下波动现象。有应力试件的分形维数普遍大于无应力试件,说明应力的存在一般会使表面更加粗糙不平。 (4)蚀坑形态以球冠状为主,有应力和无应力试件蚀坑深度分布较好地服从正态分布规律。蚀坑径深比随着质量损失率的增加趋于平稳,当质量损失率大于7%左右后径深比基本稳定在2~6,平均值在4附近波动。
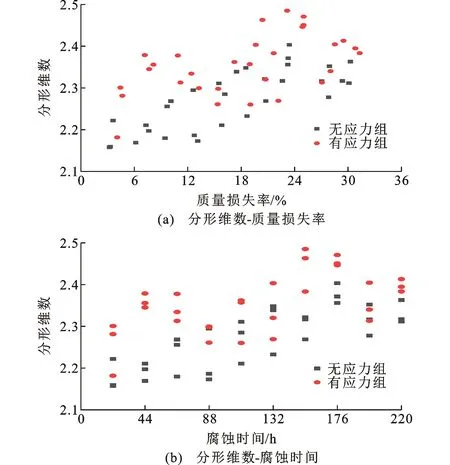
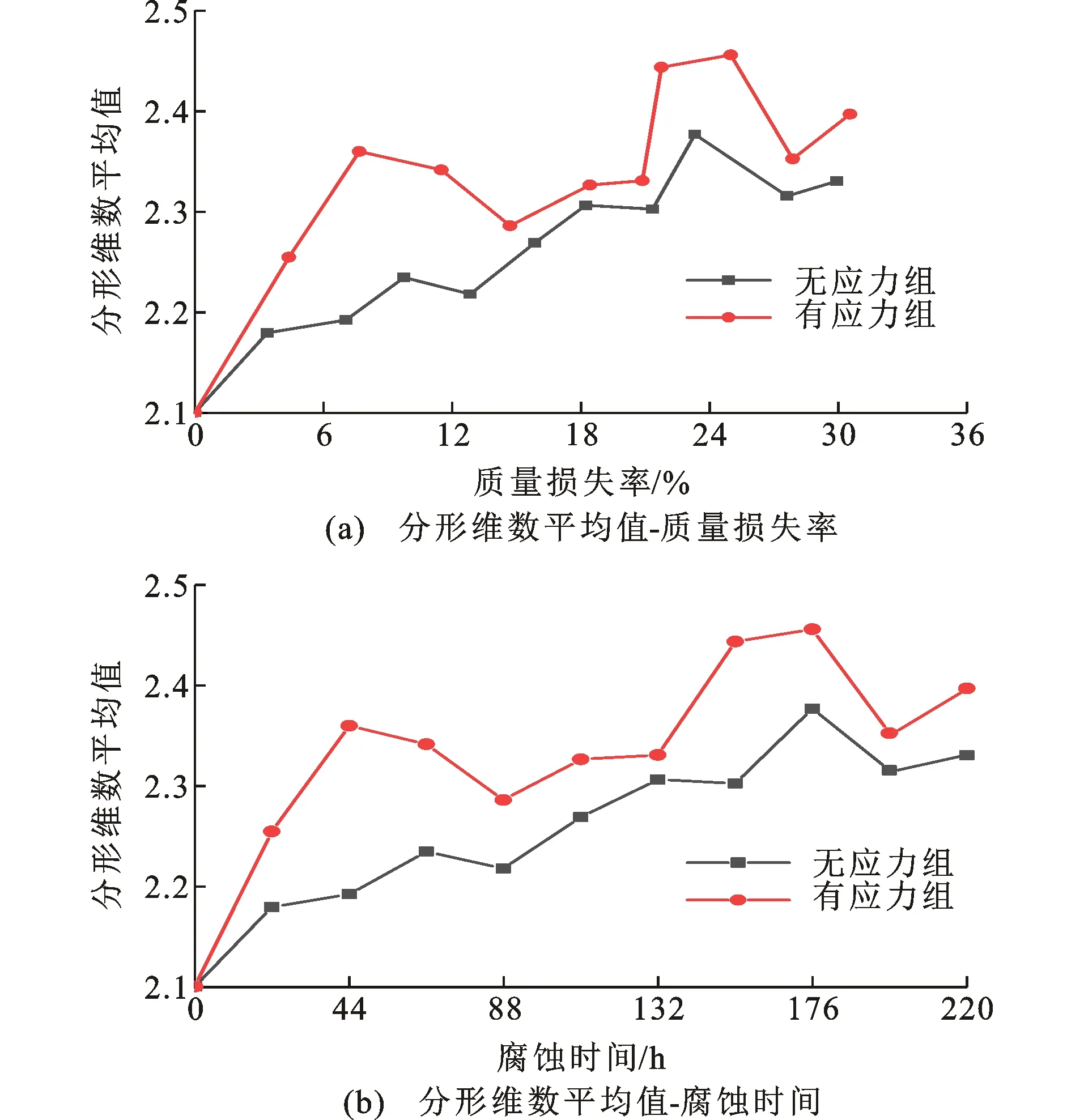
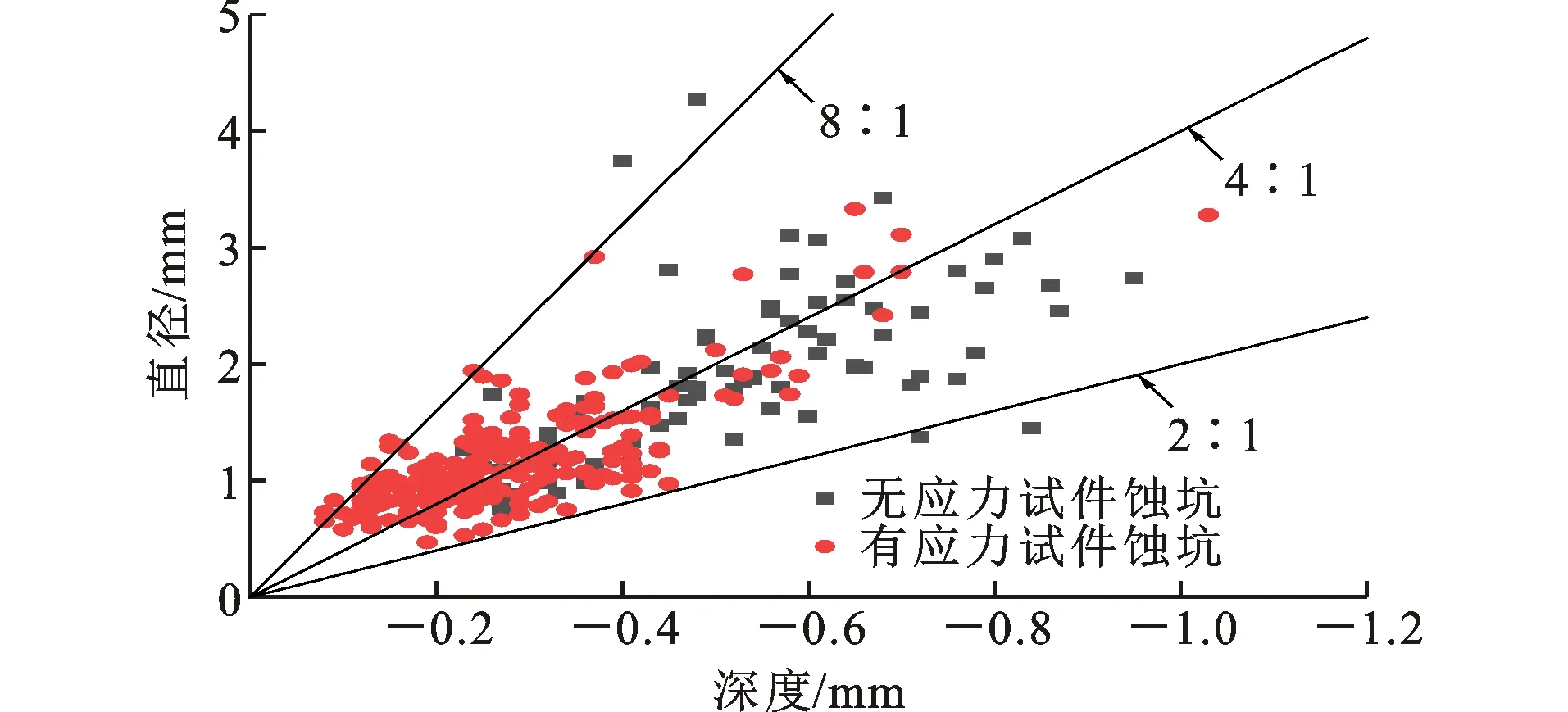
2.4 蚀坑深度分布规律与径深比规律


3 结 语
