Hilbert K_模上酉群的广义同态映射

董芳芳

(天水师范学院 数学与统计学院,甘肃 天水 741001)

Hilbert K_模是紧算子代数模，也是一种特殊的HilbertC*-模，其中底代数K为作用在Hilbert空间上的全体紧算子组成的C*-代数，即I∉K，Bakic和Guljas在文献[1]中证明了Hilbert K_模一定有特殊的标准正交基，其特殊点在于相同基向量的内积为K中的一个秩1的自伴投影.

设M和{Nj,j∈J}均为Hilbert K_模，Γj∶M→Nj为有界可伴算子集，U为作用在M上的全体酉算子组成的群(简称酉群)，在U和U(M)之间引入了一个*-同态映射τ，通过定义运算，τ(U)={τ(u),∀u∈U}也称为一个群，又通过定义M到Nj上的算子集{Γjτ(u),j∈J,u∈U}为广义标准正交基或广义(正规紧)框架来定义酉系统τ(U)的广义完全游荡向量或广义完全(正规紧)框架向量{Γj,j∈J}，展开了本文的研究.

1 预备知识

定义1[1]设K为作用在Hilbert空间Η上的全体紧算子组成的C*-代数，Μ是复数域C上的线性空间，Μ是左K_模，满足μ(kx)=(μk)x=k(μx)，其中任意的μ∈C，k∈K，x∈Μ，若〈·，·〉∶Μ×Μ→K具有性质

(i) 〈x,x〉≥0，∀x∈Μ；

(ii) 〈x,x〉=0⟺x=0，∀x∈Μ；

(iii) 〈x,y〉=〈y,x〉*，∀x,y∈Μ；

(iv) 〈kx,y〉=k〈x,y〉，∀k∈K，∀x,y∈Μ；

(v) 〈x+y,z〉=〈x,z〉+〈y,z〉，∀x,y,z∈Μ.

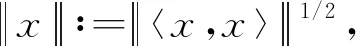
定义2[2]称可伴算子组成的集合Ω为一个群，若对任意的T1,T2∈Ω，T1T2∈Ω，T2T1∈Ω；对任意的T∈Ω，存在T-1∈Ω，并且I∈Ω.

把酉算子U={∀u∈L(M),uu*=u*u=I}组成的群称为酉群.

定义3[3]设U为作用在Hilbert K_模M上的酉群，称*-同态τ∶U→U(M)为U的一个表示，若对任意的u,v∈U，τ(uv)=τ(u)τ(v)，τ(u)*=τ(u*)，其中U(M)为作用在M上的全体酉算子组成的酉群.

注:由该定义不难验证τ(U)={τ(u),u∈U}也为酉群，且τ(I)为它的单位算子，其中I为U的单位元.事实上，对任意的u∈U，

τ(u)*τ(u)=τ(u*)τ(u)=τ(u*u)=τ(I)，τ(u)τ(u)*=τ(u)τ(u*)=τ(uu*)=τ(I).

作用在M上的酉群U的表示记作(τ,U,M).

定义4[4]设M和Nj均为Hilbert K_模，τ(U)为酉群，称M关于Nj的可伴算子集{Λj,j∈J}为τ(U)的广义完全游荡向量，若{Λjτ(u),j∈J,u∈U}为M关于Nj的广义标准正交基，即若

(ii) 对任意的gm,gn∈Nj，

定义5[5-6]设M和Nj均为Hilbert K_模，τ(U)为酉群，称M关于Nj的可伴算子集{Γj,j∈J}为τ(U)的广义完全(正规紧)框架向量，若{Γjτ(u),j∈J,u∈U}为M关于Nj的广义(正规紧)框架，即若存在a>0，b>0，使得对任意的x∈M，有

特别地，若a=b=1，则称{Γjτ(u),j∈J,u∈U}为M关于Nj的广义正规紧框架，也称{Γj,j∈J)为τ(U)的广义正规紧框架向量.

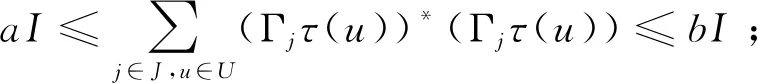
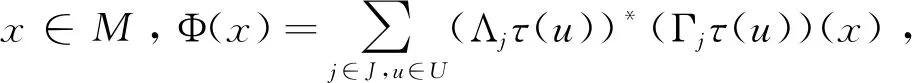
2 主要结论

定义7对酉群τ(u)，称τ(u)′={∀T,Tτ(u)=τ(U)T,u∈u}为τ(U)的换位.

定义8设U为作用在Hilbert K_模M上的酉群，称U的一个表示(τ,U,M)为一个广义框架表示，若τ(U)有广义完全正规紧框架向量.

定义9称τ(U)的两个广义完全正规紧框架向量{Γj,j∈J}和{Λj,j∈J}酉等价，若广义正规紧框架{Γjτ(u),j∈J,u∈U}和{Λjτ(u),j∈J,u∈U}酉等价，即若存在酉算子T∶M→M，使对任意的u∈U，T(Γjτ(u))*=(Λjτ(u))*.

定义10设(τ1,U,M1)和(τ2,U,M2)为U的两个广义框架表示，称τ1和τ2酉等价，若存在酉算子w∈L(M1,M2)，使得对任意的u∈U，wτ1(u)=τ2(u)w.

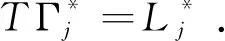
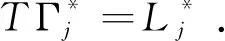
下证T∈τ(U)'.

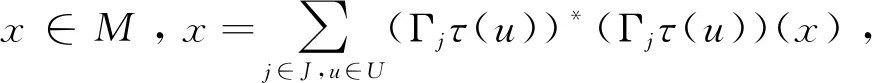
由x的任意性知Tτ(υ)=τ(υ)T，再由υ的任意性知T∈τ(U)'.

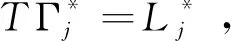
定理2设(τ1,U,M1)和(τ2,U,M2)为U的两个广义框架表示，{Γj,j∈J}和{Lj,j∈J}分别是τ1(u)和τ2(u)的广义完全正规紧框架向量,若{Γjτ1(u),j∈J,u∈U}和{Λjτ2(u),j∈J,u∈U}酉等价，则τ1和τ2酉等价.

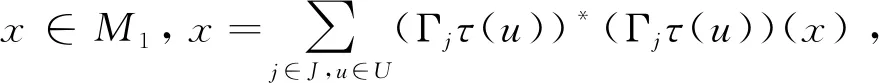
从而由x的任意性知wτ1(u)=τ2(u)w，即τ1和τ2酉等价.

定理3 设M为Hilbert K_模，τ(U)为酉群，{Γj,j∈J}为τ(U)的广义完全正规紧框架向量，{Λj,j∈J}为τ(U)的广义完全游荡向量，Φ为{Γjτ(u),j∈J,u∈U}的广义框架变换，P为M到Φ(M)的正交投影，则P(Λjτ(u))*=Φ(Γjτ(u))*，Φ*Φ=P，且P∈τ(u)′.

证明首先，由于{Γjτ(u),j∈J,u∈U}为M关于Nj的广义正规紧框架，从而Φ*Φ=I，即Φ为等距算子，而P为M到Φ(M)的正交投影，除了有P(M)=Φ(M)外，当P作用在Φ(M)上时，P=I，即P(Φ(M))=Φ(M)，于是，对任意的x∈M，∀gi∈Nj以及M关于Nj的广义标准正交基{Λjτ(u),j∈J,u∈U}，有

=〈x,Φ*(Λjτ(u))*(gi)〉

=〈x,(Γjτ(u))*(gi)〉

=〈Φ(x),Φ(Γjτ(u))*(gi)〉.

再由gi的任意性知P(Λjτ(u))*=Φ(Γjτ(u))*.

其次，由于{Λjτ(u),j∈J,u∈U}为M关于Nj的广义标准正交基，从而，对任意的x∈M，有

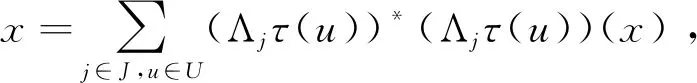
由x的任意性知ΦΦ*=P.

最后，由于对任意的u,υ∈U，uυ∈U，u*∈U，从而对任意的x∈M，

由x的任意性知Φτ(υ)=τ(υ)Φ，即Φ∈τ(u)′.

由x的任意性知Φ*τ(υ)=τ(υ)Φ*，即Φ*∈τ(u)′.

综上，由Φ∈τ(u)′，Φ*∈τ(u)′知ΦΦ*∈τ(u)′，即P∈τ(u)′.

由该定理的证明可以看出：只要{Γj,j∈J}为τ(U)的广义完全框架向量，就有Φ∈τ(u)′，Φ*∈τ(u)′，即Φ*Φ∈τ(u)′，也就是说，它的广义框架算子S∈τ(u)′，当然，当{Γj,j∈J}为τ(U)的广义完全正规紧框架向量时，更有S=I∈τ(u)′，因此有下面的推论.

推论1设M为Hilbert K_模，τ(U)为酉群，{Γj,j∈J}为τ(U)的广义完全框架向量，S为广义框架{Γjτ(u),j∈J,u∈U}的广义框架算子，则S∈τ(u)′.