一种基于L2范数的GOWA算子的中国生猪价格指数组合预测模型
2022-02-22丁伯伦房广梅刘树德
丁伯伦,房广梅,刘树德
(1.扬州工业职业技术学院 基础科学部,江苏 扬州 225000;2.安徽师范大学 数学学院,安徽 芜湖 241000)
猪肉是人们日常饮食中的重要菜品,在短期时间内能够准确预测猪肉的价格是非常有意义的.宏观层面上,相关政府部门可以根据预测结果进行猪肉市场的风险评估,合理布局市场及时出台相关政策保障市场正常运行.微观层面上,生猪饲养者可以根据预测结果规划好未来的生产任务,避免因猪肉价格的波动对生产经营造成一定的风险,猪肉加工者也可提前制定采购方案,节约采购成本.
目前学者们大多采用单一模型对生猪价格进行分析和预测.例如文献[1]提出BP神经网络模型和支持向量机对中国生猪价格指数进行预测和对比.文献[2]中采用广东省生猪在2012年-2015年的月平均价格来分析,建立了ARIMA模型,并对广东省生猪2016年月平均价格进行预测.文献[3]提出了灰色关联度分析和Stepwise回归分析的方法,研究生猪价格变化的主要影响因素,并基于BP神经网络和多元回归分析构建了BP多元回归预测模型,对未来生猪价格进行预测.文献[4]提出构建中国猪肉市场供求均衡模型,分析了影响猪肉市场供求的主要原因.近几年,学者们较为青睐组合预测模型,如利用组合模型来预测能源消费[5]、汇率[6]、商品价格[7]等.再加上组合模型具有较好的稳定性和泛化能力,因此文章拟提出一种组合模型来提高中国生猪价格指数的预测精度.
生猪价格可受多种因素的影响[8],这些因素中有线性的关系,也有非线性的关系.而灰色模型可刻画小样本数据间的线性关系,BP神经网络模型可刻画数据间的非线性关系,因此文章结合多因素灰色GM(1,N)和BP神经网络模型,并通过引入L2范数,构建了一种基于L2范数的GOWA算子的可变权系数GM-BP组合预测模型.通过实验数据对比,证明该模型是稳定的、有效的,可准确提高中国生猪价格指数的预测精度.
1 基于GM(1,N)生猪价格指数预测模型
1.1 GM(1,N)模型
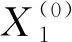
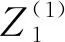
(1)
其中,a为模型的发展系数,b为驱动系数,令参数列β=[a,b2,b3,…,bN]T,令
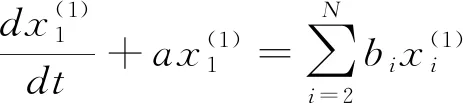
(2)

(3)
则GM(1,N)差分模拟式为
(4)
1.2 GM(1,N)生猪价格指数预测模型的建立
这里以中国2003年-2019年的生猪价格指数以及主要相关因素的历史数据来进行研究[10].运用2003年-2015年的历史数据(表1)构建GM(1,N)模型,预测出2016-2019年中国生猪价格指数.
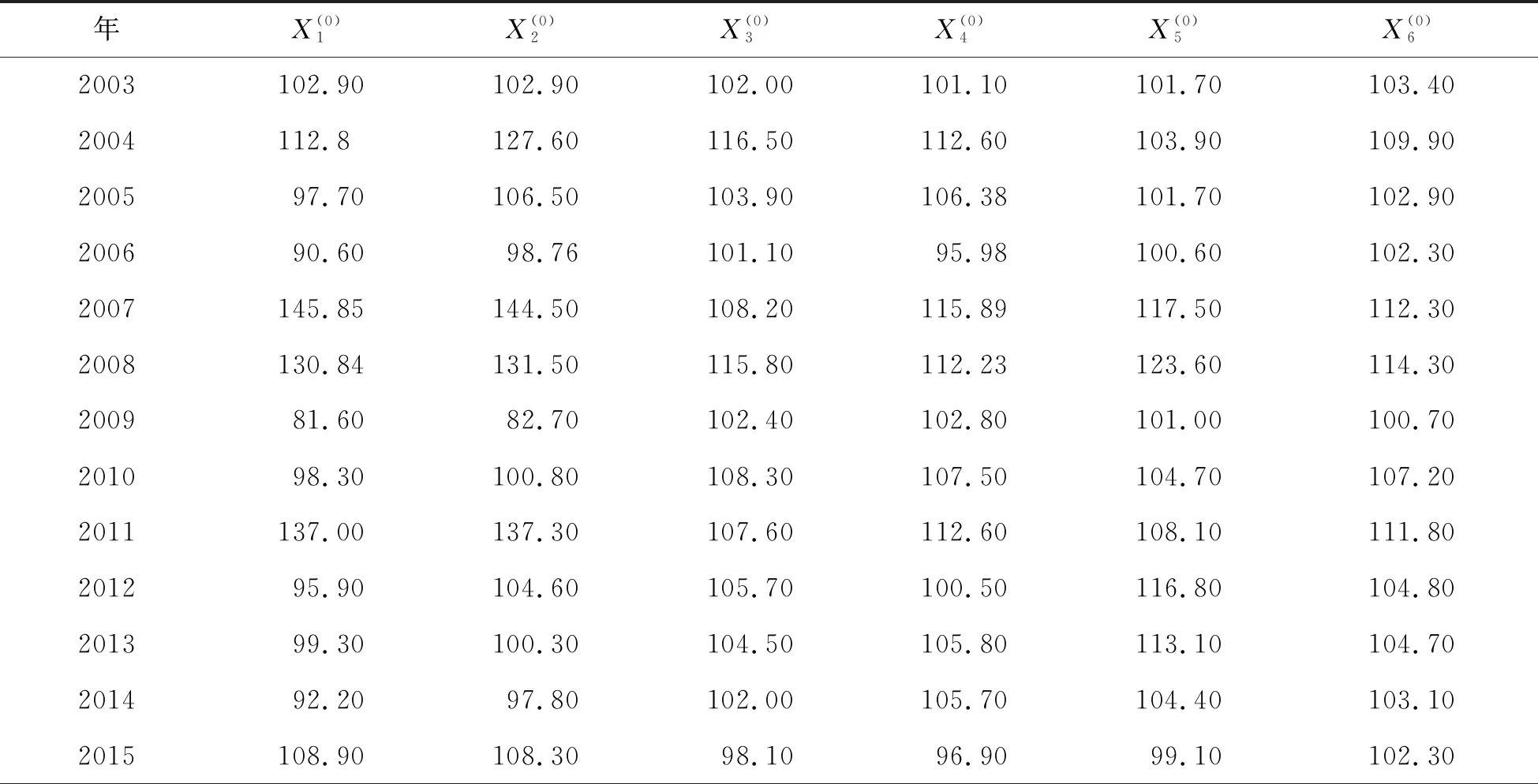
表1 我国生猪价格指数以及主要相关因素数据
相应步骤如下.

步骤3 对参数β=(BTB)-1BTY进行最小二乘估计,利用MATLAB软件求得结果如下
a=2,b=[2.058,-0.0003,0.00053,0.0003,-0.0005].
步骤4 得到GM(1,5)模型为
(5)
以及近似响应式
步骤6 利用如下还原公式,
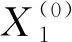
2 基于BP神经网络生猪价格指数预测模型
BP神经网络的结构由输入层、多个隐含层和输出层所构成,每层由多个神经元组成,其基本结构如下图1所示.

图1 BP神经网络基本结构
为取得一组最优权值与阈值,需要重复使用正向传播过程与误差反向传播过程来对网络进行训练学习,直至训练结束.模型对应参数连接权重值与阈值,继而进行预测直至网络输出与期望输出的误差符合之前设定的精度要求.
以表1中2003年-2015年的历史数据为训练样本,隐含层的激励函数选择Log-sigmoid型函数,输出层的激励函数是纯线性,网络训练函数是共轭梯度法,预设精度、最大训练次数以及步长分别设定为0.01、1000、0.05.网络的初始权值、学习率和阈值由网络自动选取,所建立的BP神经网络模型结构为5-7-1.利用构建的BP神经网络预测模型可对我国2016-2019年的生猪价格指数进行预测.
3 组合预测模型
将上述GM(1,N)生猪价格指数预测模型与BP神经网络生猪价格指数预测模型结合,并引入GOWA算子和L2范数,构建出了一种基于L2范数的GOWA算子的中国生猪价格组合预测模型.
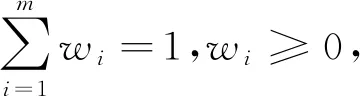
(6)
则称GOWA是n维广义有序加权平均算子,简记为GOWA算子.
(7)
则称FW为基于L2范数的GOWA的对数误差的之和,可知FW越小,预测效果越好.因此基于L2范数GOWA的中国生猪组合预测模型可表示为
(8)
4 预测结果对比分析
文章提出了基于GM(1,5)和BP神经网络的组合预测模型,为了验证组合模型的有效性和准确性,将GM(1,5)模型、BP神经网络模型和组合预测模型进行数据对比实验.
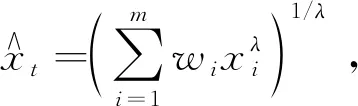

表2 不同参数取值对应下组合模型的最优权系数
通过表2对应的最优权重系数,可计算出组合模型关于中国2003年-2015年生猪价格指数的拟合结果,并将其与GM(1,5)模型以及BP神经网络模型的拟合结果进行对比分析.
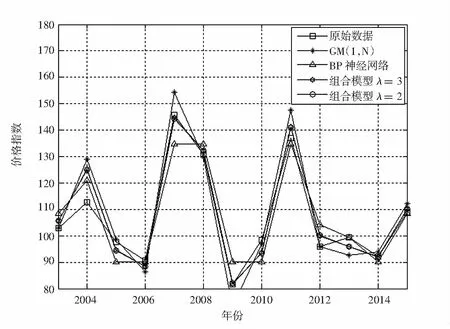
图2 各方法拟合预测对比
由图2看出,在不同参数下组合模型的预测效果较稳定,与实际值较接近,拟合的效果要优于GM(1,5)模型和BP神经网络模型.由此可见,组合模型具有较好的鲁棒性和泛化能力,因此在一定程度上能够提高预测精度.
再根据各单项预测方法的预测值,得到组合模型关于中国2016年-2019年生猪价格指数预测值,并将其与GM(1,5)模型以及BP神经网络模型的价格指数预测值进行对比,具体结果见表3.
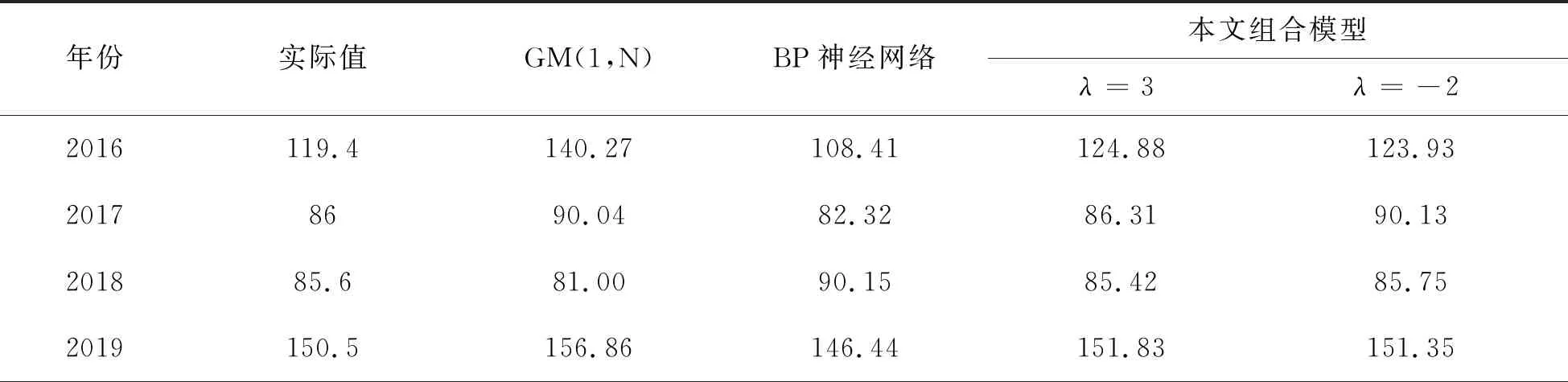
表3 各方法预测值
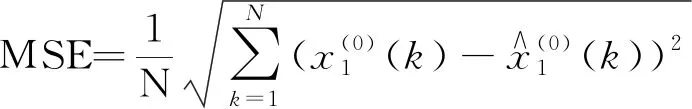
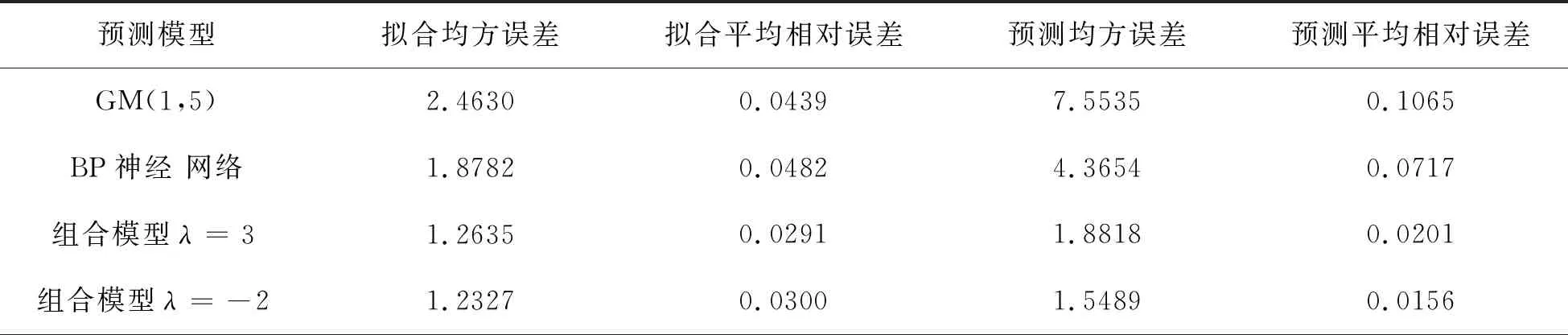
表4 各预测方法预测效果评价
由表4可知,本文提出的基于L2范数的GOWA算子的中国生猪组合预测模型的拟合均方误差、拟合平均相对误差、预测均方误差、预测平均相对误差值均小于各单项预测方法GM(1,5)模型、BP神经网络模型.因此,在一定程度上表明组合预测模型能够提高对中国生猪价格指数的预测精度.
5 结论
生猪价格指数受到多种因素的影响,文章基于其主要因素建立一种GM-BP组合预测模型,实验结果表明组合模型的预测精度较高,适合用来对我国未来生猪价格指数进行预测.组合模型对我国2016年-2019年生猪价格指数进行预测,预测的平均相对误差在0.01~0.02左右,预测精度较高.并从预测结果来看,2017年-2018年生猪价格指数相对稳定,但2018年-2019年生猪价格指数上涨幅度较大,从85左右上升到150左右,价格指数上升了约77%.通过查阅相关文献资料,明确了2019年我国生猪价格指数快速上涨的原因.环保问题加剧,2018年以来,国内大量散养户退出,以河南省为例,2018年河南省引导近100万散养户退出养猪业;瘟疫带来行业变革,截止2019年2月,因非洲猪瘟疫全国累计捕杀生猪92万头;泔水猪被禁止,受非洲猪瘟疫传播,我国全面禁止泔水喂猪,共减少了3500万泔水养猪产量;养猪意愿降低,受疫情、效益、风险等原因,很多养猪散户养殖意愿降低,生猪存栏量和出栏量都在减少,母猪存量也大幅减少,2019年数据显示母猪存栏量已跌破3000万头.
