俯冲带浅壳和上地幔地震水平向位移谱阻尼修正系数模型研究

姜妍旭，陈心锋，刘名吉

（山东建筑大学土木工程学院，山东济南 250000）

引言

近年来，由于全球自然灾害频发，造成了重大人员伤亡和财产损失，地震是对人类威胁最大的自然灾害之一。现行的《建筑抗震设计规范》（GB50011-2010）［1］和从地震动衰减关系计算得到的设计反应谱一般是针对5%阻尼比的情况。但随着减震耗能结构的广泛应用，结构的实际阻尼一般大于5%［2］，常用的5%阻尼比设计反应谱显然是不适用的，因此研究高阻尼比下的设计反应谱具有重要意义。现阶段有两种研究不同阻尼比反应谱的解决方法：一是统计分析各个阻尼比的地震动衰减关系得到不同阻尼比的反应谱，如AKKAR 等［3］和杨青松［4］；二是建立阻尼修正系数（Damping Modification Factors）模型，该研究即采用了第二种方法，通过5%阻尼比设计反应谱乘以DMF 得到其他阻尼比下的反应谱。位移谱阻尼修正系数Bd可以表示为［5］：

式（1）中：Sd(T,ζ)、Sd(T,5%)分别表示阻尼比为ζ和5%时位移的最大反应。美国地震工程协会针对DMF模型做了大量的研究工作，通过DMF对5%阻尼比设计反应谱进行修正的方法得到广泛应用。

DMF 模型的研究工作最早由NEWMARK 等［6］利用1973 年加州14 条地震动的水平和竖向分量，提出了低于20%阻尼比情况下的DMF 表达式。由于表达式中唯一参数是阻尼比，形式简单且与谱周期无关，类似的表达式被大量应用于各国抗震规范中，例如欧洲现行规范（EC8-2005［7］和NEHRP-2009［8］）。但随着地震灾害程度的增加，在后续的抗震设计研究工作中，许多学者考虑到更多因素影响，提出了更加完善的DMF模型。

近年来研究的模型，更多地加入了场地条件和谱周期这两个参数，如蒋健等［9］研究发现场地分类对阻尼修正系数的影响较大，阻尼比过大时结构位移降低显著，但不能有效减小地震力；LIN 等［10］发现由加速度谱导出比由位移谱导出的DMF 对场地类别更敏感，给出与阻尼比、谱周期及场地条件有关的非线性表达式；HATZIGEORGIOU［11］通过考虑四种场地条件的位移、速度和加速度谱，证明了DMF受结构自振周期的影响；刘名吉等［12］考虑谱周期，阻尼比及场地条件的影响给出俯冲带地区竖向位移谱DMF 模型，并得到震级和震源距对模型有显著影响。

部分学者研究了震源、路径效应等参数对DMF 的影响。CAMERON 等［13］研究发现DMF 受矩震级、断层矩和场地类型等的影响，当阻尼比为1%时，DMF还取决于台站到震源的距离，该因素影响地震动持续时间。DANESHVAR 等［14］利用加拿大东部地区8 次地震108 条加速度记录和540 条由随机有限断层模型生成的人工记录，发现DMF尤其在较长周期对震级变化敏感，而距离对DMF的影响不显著；LI等［15］研究发现：DMF与振动周期密切相关，阻尼比对加速度谱的影响随震级和震源距离的增大而增大，在近场的小地震，场地类别对DMF有显著影响，但随着震级和震源距离的增加，影响程度减小，而上述地震动参数产生的影响是与地震动频率分量的相对衰减有关。

当5%阻尼设计谱与震级和震源距离等参数无关时，或者即使反应谱是从概率危险性分析研究中得出：该地震的震级和震源距也可能随谱周期变化，这种情况下应该使用没有震源和路径参数的DMF模型。因此本文对俯冲带浅壳和上地幔地震强震记录进行分析，建立只考虑阻尼比、场地类别和谱周期的水平向位移谱DMF 模型，以调整5%阻尼比的位移谱，应用于无法确定震源和震源距离的实际工程设计。利用ABRAHAMSON 等［16］随机效应模型分离出残差及其对应的残差标准差，探究震级、震源距离和断层深度等因素对模型的影响。

1 地震数据来源与场地分类

本文选取日本的K-net和KiK-Net强震台网中Mw≥4.9的6 466条俯冲带浅壳和上地幔水平向强震记录进行研究。本文采用Slab1.0 俯冲带几何模型，结合日本地震分类方法［17］，并参考ZHAO（2006）等［18］的基于场地周期Ts的场地分类方法对数据进行了处理。所有记录台站都有一个向下至工程基岩的实测剪切波速剖面，以便进行场地分类。场地类别将数据记录分为四组，分别对应四种不同的场地条件。场地周期Ts由式（2）计算得到：

式中：H为基岩顶部到场地地表的深度，单位为m；Vsite为基岩上覆土层平均剪切波速，单位为m/s。

表1 列出了该分类方法的场地类别分类标准及不同场地的记录数量，并列出了相应的NEHRP（National Earthquake Hazards Reduction Program）场地分类标准［19］。

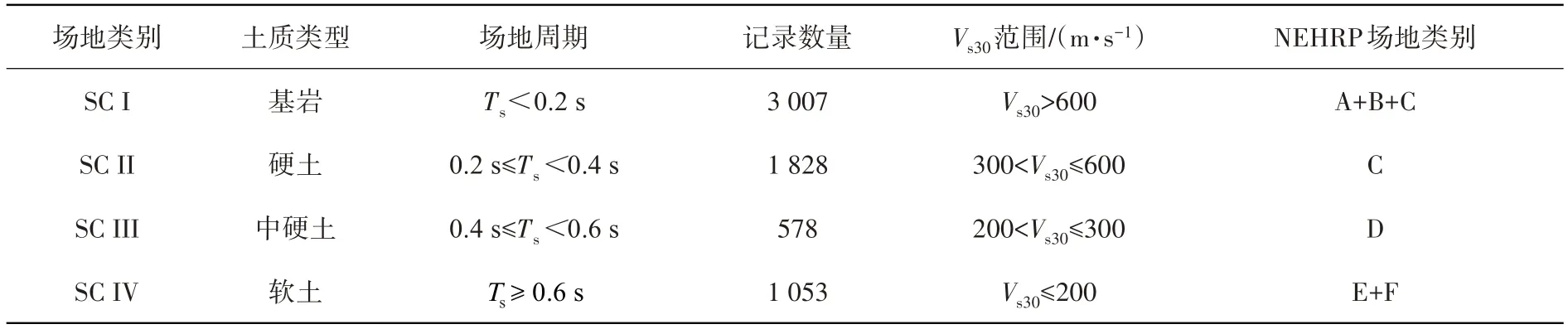
表1 场地类别分类标准及不同场地记录数量Table 1 Definition of site class and number of records of different site classes

2 建立阻尼修正系数模型

2.1 各类场地DMF均值模型对比

该研究针对选取的地震动记录计算了13 个阻尼比（1%～4%、6%～10%、15%、20%、25%、30%）和36 个周期（0.01～5.0 s）的位移反应谱，得到四种场地条件下的B（d不同阻尼比的位移谱与5%阻尼比位移谱的比值）均值，其中：阻尼比为1%、3%、10%和30%的SC I、II、III和IV四种场地的Bd值与谱周期的关系曲线，如图1所示。

图1 SC I～SC IV四类场地Bd均值分布Fig.1 Geometric mean values of Bd for four site classes and damping ratios

为考虑场地对DMF模型的影响，假设该组数据服从正态分布。本文采用Z检验的方法验证不同场地条件下的阻尼比修正系数均值的差异性，判断该差异是否显著。本文采用置信水平为5%，拒绝域 |Z|≥1.96，公式为：

式中：Z为统计量；和分别为两种场地下的DMF 均值；和为同一周期下DMF 均值的样本方差；nx和ny分别表示两类场地各自的样本数。当拒绝域 |Z|≥1.96 时，则总体差异性显著。文中对比每两组数据间的统计参数的差别，而不是确定每组参数本身的统计差别。

图2 给出了1%和30%阻尼比情况下，SC I～SC IV 场地间显著性检验的分布图。由图2（a）、图2（b），图2（c）和图2（e）表明：在阻尼比1%和周期在0.02～0.18 s 期间时SC I 与SC II 场地、SC I 与SC III 场地，SC I 与SC IV 场地和SC II与SC IV DMF 值在统计上显著不同，其 |Z|值在较多周期都远远大于1.96，最大的超过40。在相同的谱周期上，SC II与SC III和SC IV 的|Z|值相对较小但在相同周期范围统计上不同，但从实际应用角度上差别不大。在周期大于0.3 s，SC I 与SC IV，SC II 与SC III 和SC II 与SC IV 场地DMF 差值统计上显著且|Z|较大。虽然SC III和SC IV类场地的|Z|值在很多周期上大于1.96但与其它场地类别相比较小，表明两类场地的DMF值差别不大。图2（a）、2（b）、2（c）和2（e）中的|Z|值在0.07 s周期处出现较大的峰值，引起峰值的原因是SC I场地的共振现象，即在场地共振周期，阻尼比的影响最大。图2（b）和图2（d）中出现在0.5 s的第二峰值是由SC III类场地的共振现象引起的，而图2（c）和图2（e）的第二个峰值是SC IV场地的共振引起的。在30%阻尼比情况下，所有两个场地类别之差在0.15 s 以内谱周期统计上显著且|Z|值较大。在谱周期大于大约0.2 s 时，各两类类场地之差的|Z|值相对较小且在有些谱周期上小于1.96。阻尼比较大时，共振现象起的不同场地类别的阻尼比值不明显。可见不同场地对DMF 有显著影响，分场地类别建立DMF 模型是有必要的。

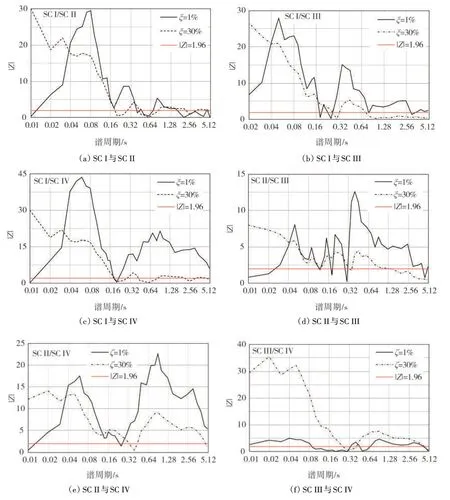
图2 四种场地的显著性检验统计值Fig.2 |Z|values for the statistical tests between each pair of SC I～SC IV site classs

2.2 DMF均值分析

该研究的DMF 模型不含震源和路径参数，但需考虑场地条件的影响，因此研究的原始数据为各类场地中的DMF均值。其中前两个谱周期（0.01 s和0.02 s）的DMF非常接近1.0。

以三个谱周期（0.05 s，0.35 s，5.0 s）为例，如图3 所示，图中散点为SC I～SC IV 类场地的DMF 对数值关于阻尼比对数值ln(ξ)的分布，实线为对应散点的二次多项式拟合趋势线。由图可得：散点拟合结果良好，在其他谱周期也有类似的结论。这表明采用阻尼比对数值的二次多项式能够很好地模拟阻尼比对阻尼修正系数的影响。

图3 DMF对数值关于阻尼比对数值的分布Fig.3 Distribution of with respect to ln(ξ)

2.3 DMF模型的形式

在建立DMF模型之前，本文参照现有研究成果［20-24］，考虑阻尼比和谱周期对DMF的影响，给出四种场地条件下的DMF模型的二次函数表达式：

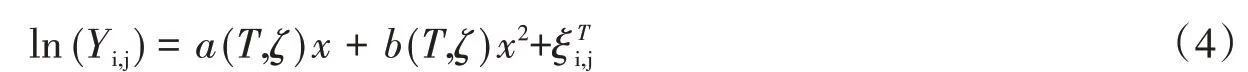
式中：Yi，j是阻尼比为ζ时第i个地震事件下第j条地震记录计算得到的DMF几何均值；x=ln(ζ/5)用于模拟阻尼比效应，ζ用百分数表示；a和b表示方程的回归系数；表示总残差。

确定回归方程之后，参数的回归按照如下步骤进行：谱周期在0.1～5.0 s 范围内的数据分为36 组，每一组数据采用利用最小二乘法（固定效应方法），按照回归方程式（4）进行系数回归，得到对应的a和b值；由于一次得到的系数不能保证DMF 曲线光滑，因此对系数a值进行平滑，将平滑后的结果代入回归方程式反算出b值；对新的b值进行平滑，将平滑后的结果代入回归方程式反算出a值；重复上述两步，最终得到足够平滑的曲线模型，回归得到的系数a和b见表2，其他谱周期的回归系数可由表中数据用线性内插法得出。

表2 模型回归系数Table 2 Model coefficients for theDMF models

图4给出了SC I～SC IV四种不同场地条件下的DMF回归值与原始数据的对比。从图中可见：回归值的走向与实际数据走向相同，数据拟合良好，仅SC I场地的1%阻尼比下0.16～0.32 s之间存在较小差异，证明了该回归方程的合理性。

图4 DMF平滑模型Fig.4 Smoothed model of DMF for four site classes

3 残差分析

从上述DMF 模型可以看出：回归表达式对总体均值拟合良好。为进一步分析残差来源，也可以进一步评估DMF 的拟合效果，需要对残差及标准差进行分析，探究引起误差的影响参数。该研究利用随机效应模型将残差分为事件间残差和事件内残差［16］，并计算其标准差。

总残差是指同一场地类别下根据单自由度系统计算的DMF 自然对数的均值与均值模型自然对数值的差值，残差定义如式（5）所示：

式中：ξi,j为第i个地震的第j条强震记录的事件内残差，均值为0，标准差为σ；ηi为第i个地震事件的事件间残差，均值为0，标准差为τ。标准差间的关系见式（7）：

式中，σT为总残差。

本文建立的DMF模型是为了调整无震级和震源距离等参数的设计反应谱，因此没有将震源和路径效应因素考虑在内。但是在实际工程中，上述参数的影响是显著的。图5 给出了谱周期0.12 s，阻尼比30%时的事件间残差随断层深度和震级变化的分布图。由图5可知：事件间残差在水平0轴的上下两侧分布不均，断层深度的拟合曲线斜率较小，而震级的拟合曲线斜率明显，这说明事件间残差与震级和断层距离都存在相关性。

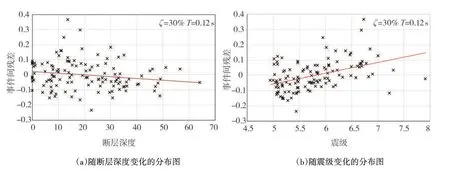
图5 30%阻尼比周期0.12s事件间残差分布图Fig.5 Distributions of between-event residuals for a damping ratio of 30%and at a spectral period of 0.12s

图6 给出谱周期为0.12s，阻尼比为30%时的事件内残差随震源距离和震级变化的分布图，可以看出事件内残差在水平0轴的上下两侧分布比较均匀，与震级无明显相关性，而相对于震源距离倾斜明显。

图6 30%阻尼比周期0.12s事件内残差分布图Fig.6 Distributions of within-event residualsfor a damping ratio of 30%and a spectral period of 0.12s

从上述残差分布结果可以看出：本文提出的DMF 模型可用于调整不考虑地震动参数的设计反应谱，要想对DMF 进行更好的拟合，在回归表达式中加入震级和震源距离等参数是十分必要的，今后将致力于建立更加完善的DMF模型。

4 标准差分析

表3-表5 分别给出回归模型的总残差标准差，事件间残差标准差和事件内残差标准差。标准差越小，说明拟合度越好。

表3 总残差标准差Table 3 Total standard deviations

表4 事件内残差标准差Table 4 The within-event standard deviations

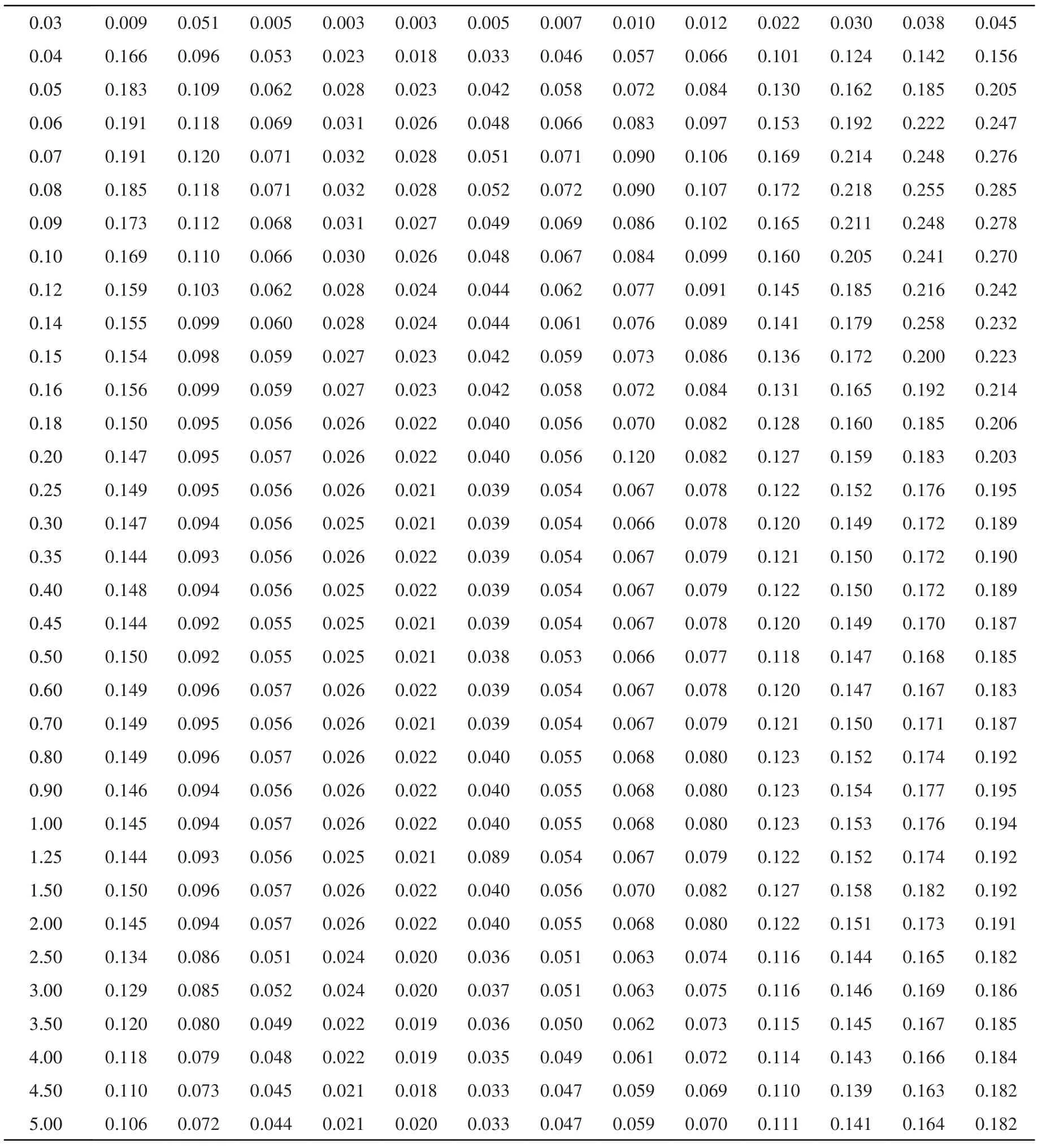
续表

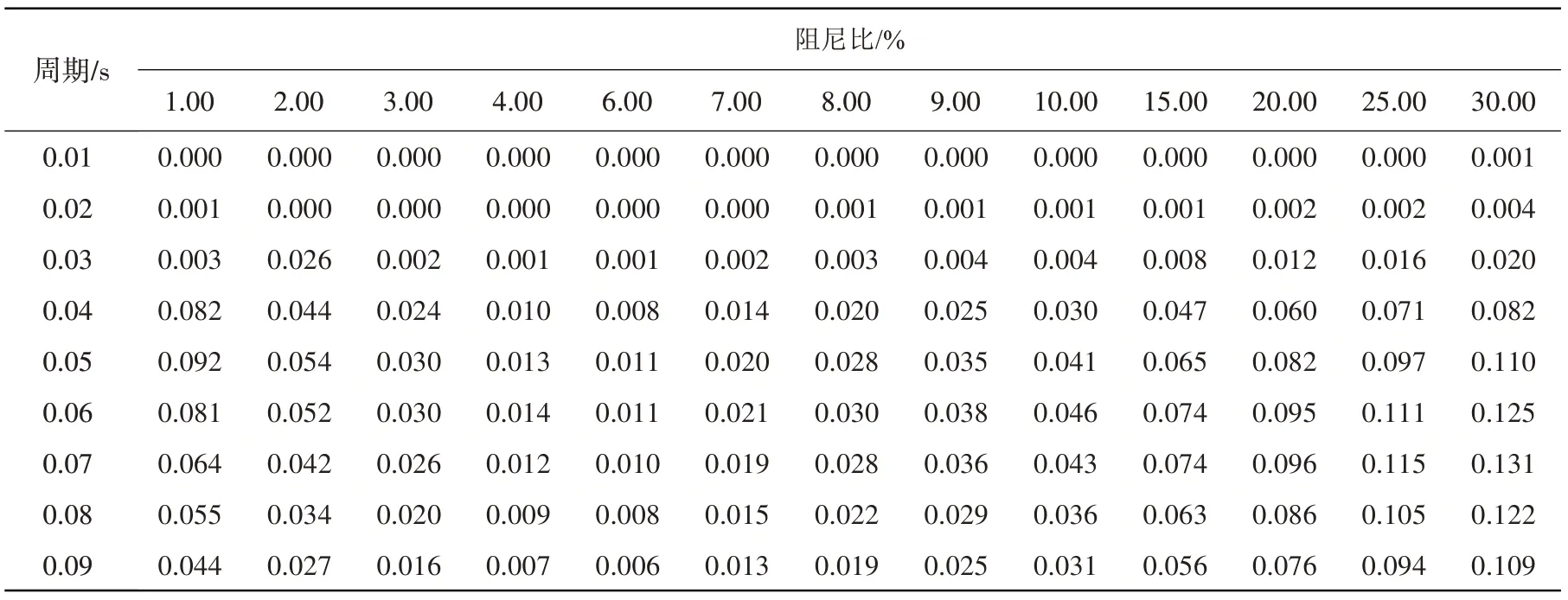
表5 事件间残差标准差Table 5 Between-event standard deviations

续表

图7 分别给出阻尼比为1%、3%、15%和30%时事件内标准差σ、事件间标准差τ、总标准差σT随谱周期变化的分布图。在大多数谱周期内，事件内标准差大于事件间标准差，如图7（a）所示，在阻尼比为1%时，事件间标准差远小于事件内标准差，在其他阻尼比短周期内类似，这表明震源效应比路径效应和场地效应模拟得更好；谱周期小于0.02 s 时，三类残差标准差接近于零，此时位移谱与阻尼比无关，残差为零；随周期和阻尼比的增大，事件内标准差与事件间标准差差值逐渐减小，当阻尼比大于15%，周期大于3.5 s时事件间残差标准差大于事件内残差标准差，这表明在长周期部分，DMF 模型受震源效应的影响比路径效应和场地效应更为显著。

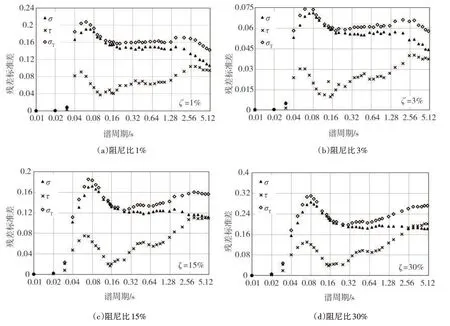
图7 残差标准差随谱周期分布图Fig.7 Distribution of standard deviations of σT，σ and τ

与地震动衰减模型相比［25］，总体上本文模型的各类标准差很小，只有在长周期和大阻尼比的情况下这些标准差才会对地震风险评估有一定的影响，而在其它大多数周期和阻尼比上可以忽略不计。这些较小的标准差表明各个阻尼比的反应谱模型的残差高度线性相关，其残差的相关的部分在计算DMF过程删除了这些相关误差。

5 结论

基于K-NET和KiK-Net强震台网中的6 466条俯冲带浅壳和上地幔强震记录，按场地周期将上述数据划分为四组，对应四种场地条件，分别建立水平向位移谱阻尼修正系数模型。在回归分析中，利用最小二乘法建立位移谱DMF 的均值模型，并应用了随机效应模型方法将总残差分为事件内残差和事件间残差，进一步探究了震源效应和路径效应等影响。本文得到的结论如下：

（1）通过Z检验可知：相同阻尼比下，场地类别对DMF 均值影响显著，分四种不同的场地条件建立阻尼修正模型效果更好。

（2）DMF均值模型考虑阻尼比和谱周期的影响，通过最小二乘法得到阻尼比对数的二次函数表达式，能够很好地拟合四种不同场地条件的DMF模型。

（3）模型事件间残差与震级和断层深度有相关性，事件内残差与震源距离显著相关。

（4）在谱周期0.01～5.0 s内，震源效应的影响显著小于路径和场地等效应引起的误差。而在大部分谱周期中，路径及场地等效应引起的误差最大。

（5）震源距、震级和断层深度都会影响DMF模型，由于本文研究是为了调整无震级和震源距离等参数的设计反应谱，今后将致力于建立更加完善的DMF模型。