主余震作用下高强钢筋混凝土框架的易损性分析
2022-02-19张健新
刘 平,王 超,张健新
(1.河北工业大学土木与交通学院,天津 300401;2.河北省土木工程技术研究中心,天津 300401;3.中国民航大学,天津 300300)
引言
地震灾害的经验表明:一次主震(强震)后往往会发生一次或多次较大震级的余震,由于地震的时间间隔短,无法对受损结构进行修复和加固,余震产生的“二次损伤”可能使结构严重破坏甚至倒塌。因此研究主余震作用下结构的抗震性能十分必要,众多学者也进行了主余震作用的相关研究[1~3]。吴波等[4]和欧进萍等[5]对主余震作用下的累积损伤进行了研究,并提出了相应的损伤模型和设计方法;RAGHUNANDAN 等[6]研究了主震中结构的破坏程度与余震倒塌能力的对应关系,量化了视觉评价标准的物理指标,快速预测结构的余震倒塌能力;周洲等[7]研究了框架结构在单独主震和主余震作用下的地震易损性,从概率角度对余震损伤进行了量化,并对比了主余震序列的不同构造方法对易损性的影响;杨福剑等[8]利用局部和整体的损伤耗能评价主余震的累积损伤;FABIO 等[9]对主余震作用下填充墙框架的易损性做了评估;SONG 等[10]研究了主余震激励的自定心混凝土框架的概率地震需求。
高强钢筋在混凝土结构构件方面的试验研究显示其具有较好的性能,而对高强钢筋混凝土整体框架的研究相对较少,对主余震作用下高强钢筋混凝土整体框架的研究更少。本文以配置高强钢筋的混凝土框架作为研究对象,构造人工主余震序列,采用增量动力分析法(IDA)进行易损性分析,对比不同主震强度下的易损性曲线,分析主震强度对主余震易损性的影响,同时分析钢筋强度等级对结构抗震性能的影响。
1 结构设计与建模
1.1 框架设计
根据《建筑抗震设计规范》(GB 50011-2010)设计了三榀六层四跨的钢筋混凝土框架KJ1、KJ2和KJ3,如图1 所示,采用相同的结构形式和截面尺寸,按照“等强代换”原则进行配筋,即fy1As1=fy2As2,式中:fy1和fy2分别为两个框架结构钢筋的屈服强度设计值;As1和As2为两个框架结构中对应部位所需配置的钢筋面积,该原则可以保证框架结构具有相同的设计水准和基本一致的钢筋用量。首层层高3.9 m,2~6 层层高3 m,抗震设防烈度8度,设计基本加速度0.2 g。荷载条件:楼面恒载3.5 kN/m2,屋面恒载5.0 kN/m2,楼面活载2.0 kN/m2,屋面活载2.0 kN/m2。KJ1、KJ2和KJ3的混凝土强度等级均为C35,纵向受力钢筋分别为HRB400、HRB500和HRB600。等效的均布荷载及集中荷载见表1。钢筋参数见表2。
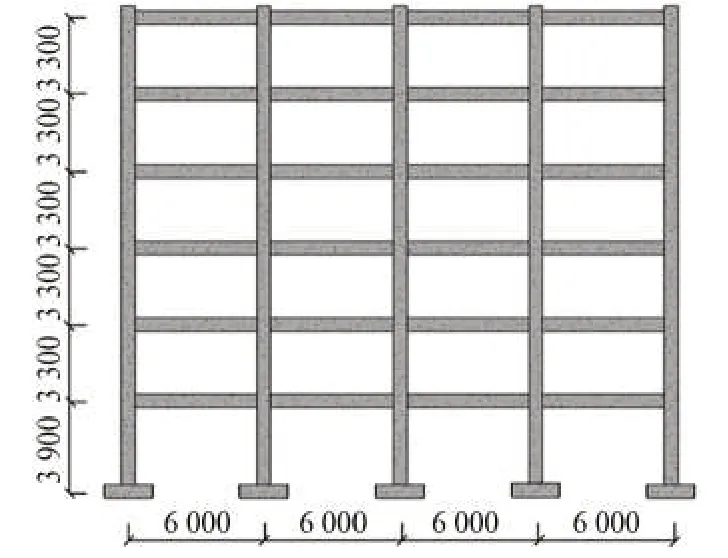
图1 框架立面图Fig.1 Elevation of the frame

表1 各层荷载值Table 1 Load of each floor
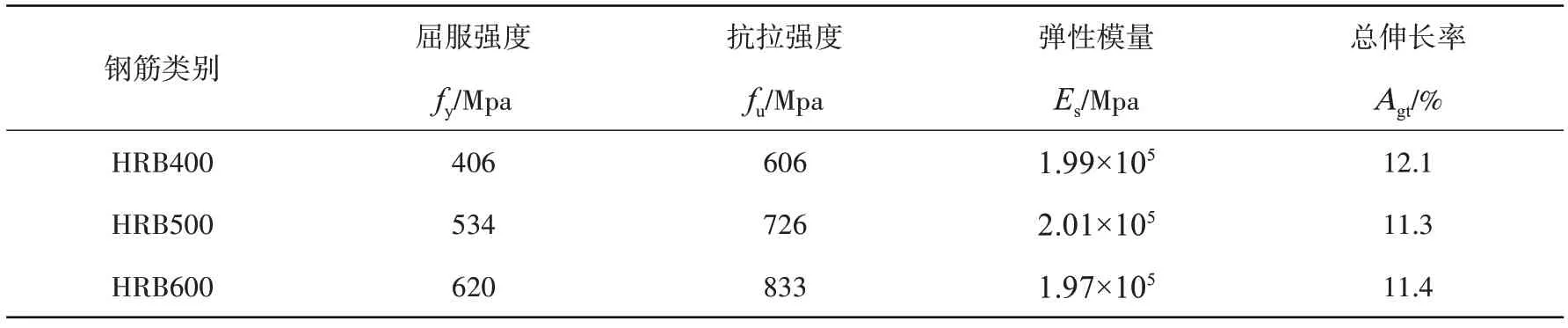
表2 纵向受力钢筋参数Table 2 Parameters of longitudinal reinforcement
1.2 OpenSees模型
截面和单元的划分对有限元模拟的精准度有重要影响。本文对框架节点区域的建模如图2所示。在梁柱相交的节点部位采用弹性截面,设置足够大的弹性模量模拟节点范围的刚域。对梁和柱其他部位的单元赋予纤维截面。模型中所有单元均采用基于位移的非线性梁柱单元,设置5个积分点,并通过增加单元数量来保证计算精度。在靠近梁端和柱端位置为可能的塑性铰区,要求单元长度小于塑性铰长度,因此单元长度取为构件高度的一半,以提高强非线性区的模拟精度,体现地震损伤。纤维截面划分如图2 所示。将梁和柱的纤维截面划分为核心区混凝土、保护层混凝土和钢筋三种纤维,核心区混凝土采用Concrete02 本构模型,通过Mander 理论考虑箍筋对核心区混凝土的约束作用。保护层混凝土为Concrete01,不考虑混凝土的受拉。纵向受力钢筋采用基于Giuffre-Menegotto-Pinto 等向硬化材料的Steel02 本构模型,能反应反向加载过程中的包辛格效应。由于框架在强震作用下可能存在纵筋拉断的情况,因此本文采用以Steel02 为基础材料的MinMax 模型模拟钢筋断裂,该模型认为基础材料应变达到设定的阈值后,材料强度突变为0,即认为材料失效。
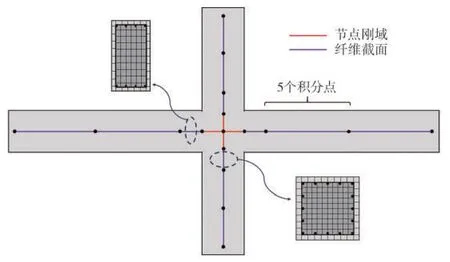
图2 节点范围建模Fig.2 Model of joint
1.3 模型验证
2011年清华大学完成了钢筋混凝土整体框架的拟静力倒塌试验[11],并公开了相关试验数据和图像。采用1.2 节中的建模方法,根据给出的结构、截面尺寸及材料参数进行建模,按照相同的加载模式进行静力分析,得到基底剪力和顶点位移的滞回关系曲线及骨架曲线,并与试验结果进行对比,如图3 所示。可以看到试验结果与模拟结果的滞回曲线吻合良好,骨架曲线发展趋势基本一致,各特征点和峰值点基本吻合,证明了本文建模方法模拟整体框架抗侧力性能的有效性。
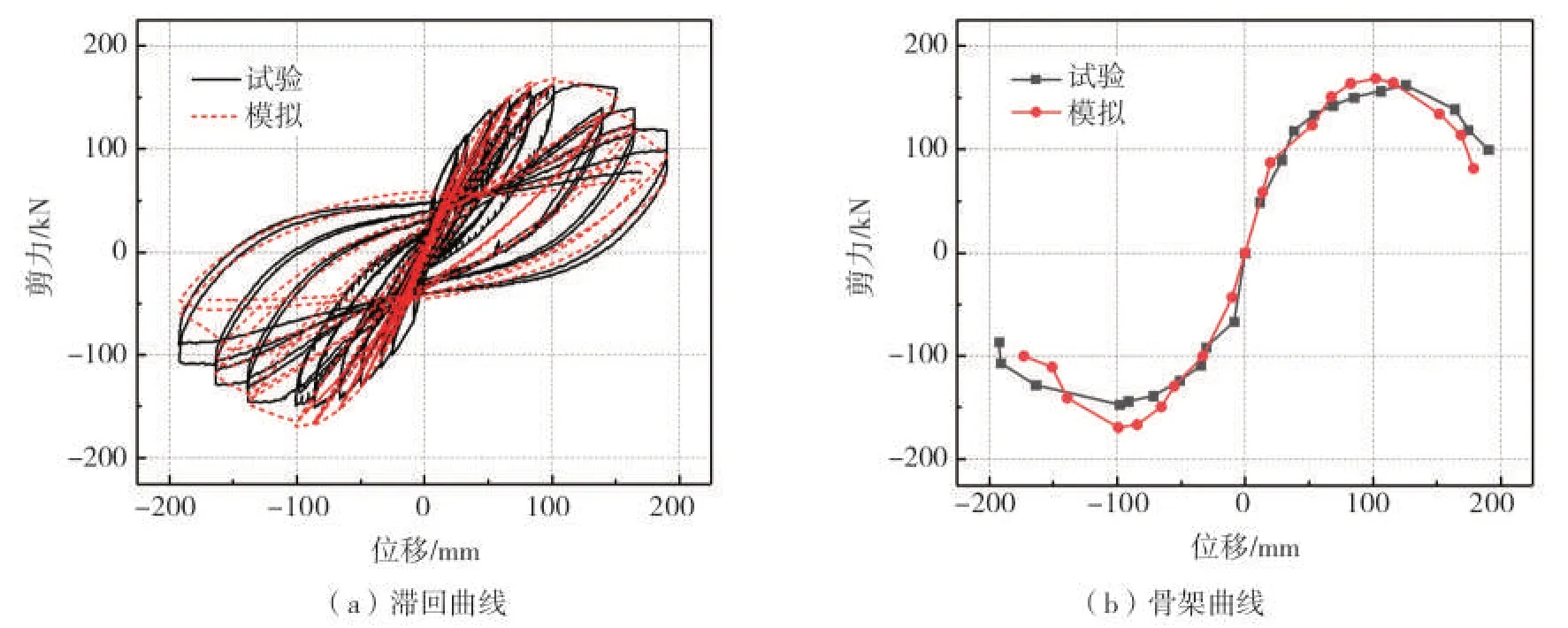
图3 试验模拟对比Fig.3 Contrast between simulationand experiment
2 增量动力分析
2.1 IDA参数确定
IDA 曲线是地震动强度指标(IM)与结构损伤指标(DM)的关系曲线。本文将地震峰值加速度(PGA)作为IM 指标[9]。结构损伤指标主要有能量类指标、Park-ang 双参数指标和位移类指标等,为震后测量方便,本文将最大层间位移角(位移类指标)作为DM 指标[6]。《建筑抗震设计规范》(GB 5001-2010)在抗震变形验算中给出了楼层最大层间位移角的弹性限值[θe]=1/550,和弹塑性限值[θp]=1/50,以此作为轻微破坏和毁坏两种极限状态的层间位移角限值,将2[θe]和4[θe]分别作为中等破坏和严重破坏的位移角限值,由4个限值划分了5 个破坏等级,见表4。美国(ATC-63)[12]在其地震动记录集中推荐了22 组远场记录和28 组近场记录,主要选波原则为:震级6.5 以上;震源处于走滑和逆冲断层;远场和近场地震以(RCR+RJB)/2=10 km 为区分;场地剪切波速大于180 m/s;地震记录PGA≥0.2 g,PGV≥15 cm/s;强震有效周期达到4 s以上;观测对象为低层建筑的首层地面或自由地表。本文选取其中15条地震记录的加速度时程用于IDA 分析,见表3、图5。采用重复法构造主余震序列,在地震调幅时,首先将主震PGA 依次调幅至0.4 g、0.7 g 和1.0 g,对于每一主震后的余震采用等步长法进行调幅,步长为0.1 g,余震PGA 依次从0.1 g 调幅11 次至1.2 g,使结构经历弹性和弹塑性直到破坏的各个阶段,对余震的调幅也避免了重复法构造主余震序列损伤偏大的情况。此外,考虑到地震的实际情况,在两次地震之间设置20 s的时间间隔,以保证主震后结构响应充分完成,同时保留主震的塑性损伤。主余震的构造方式如图4所示。
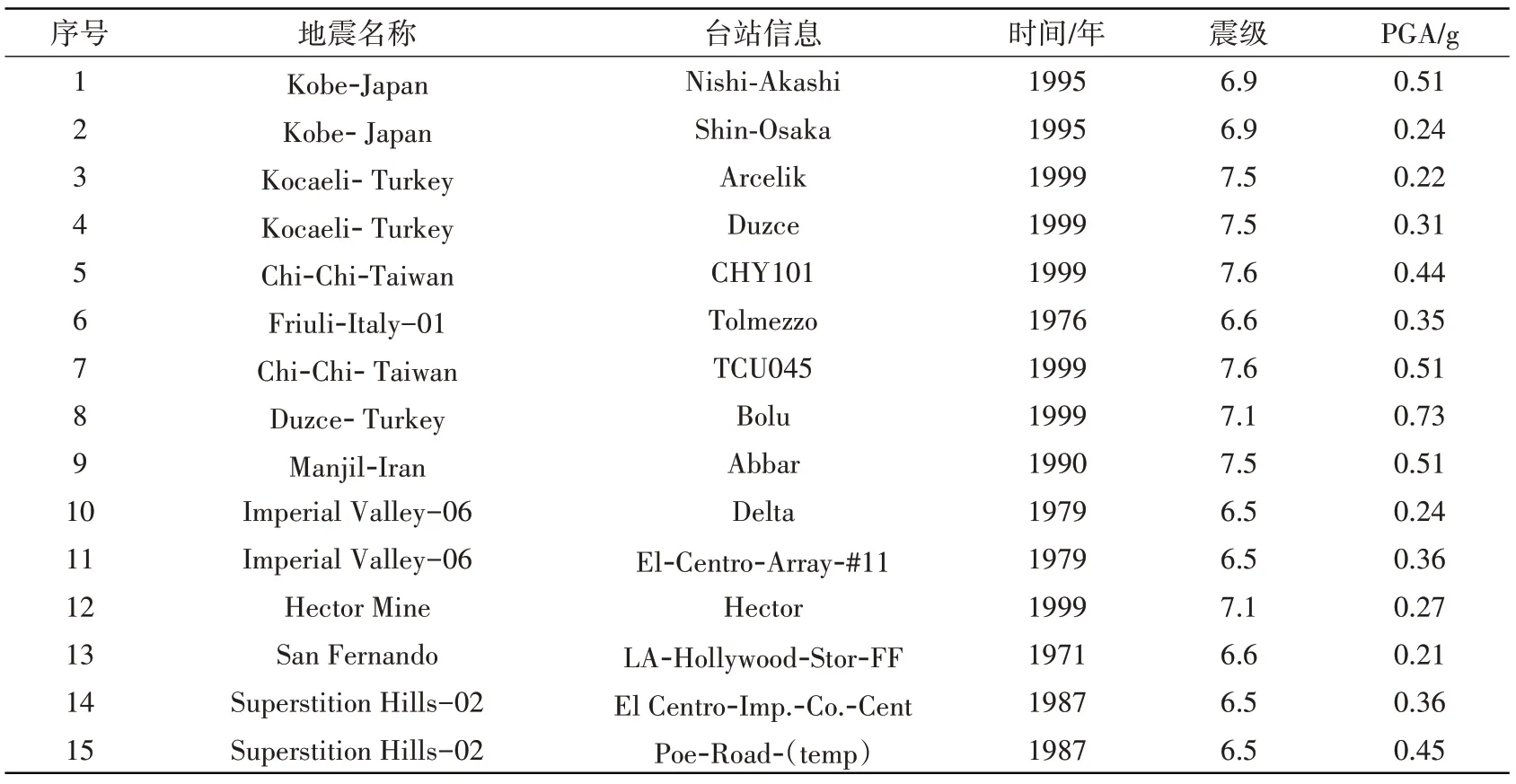
表3 地震动信息Table 3 Seismic information
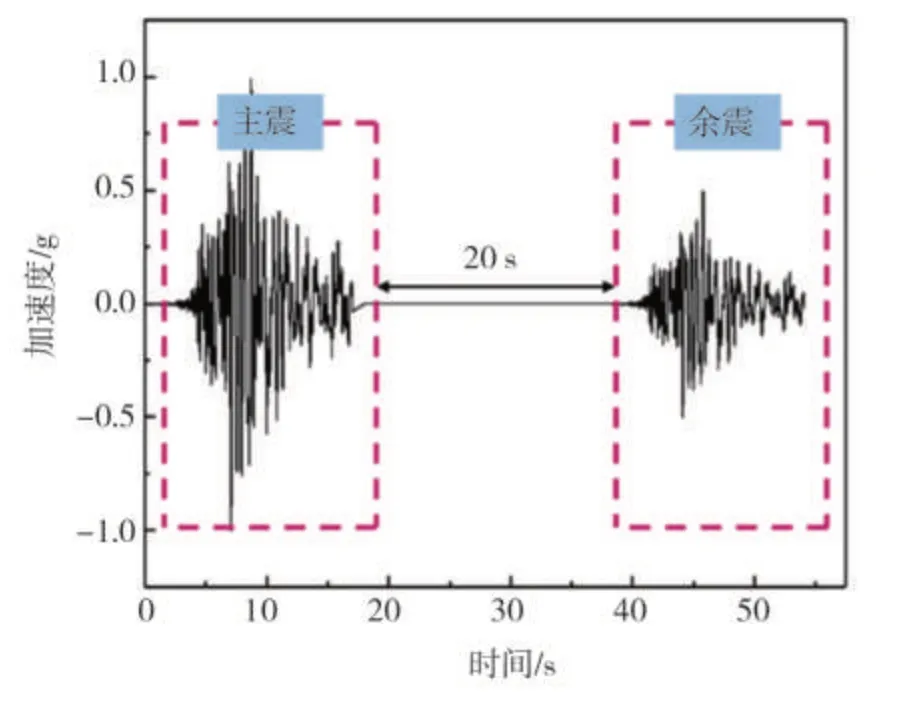
图4 人工主余震序列 Fig.4 Artificial main-aftershock sequences
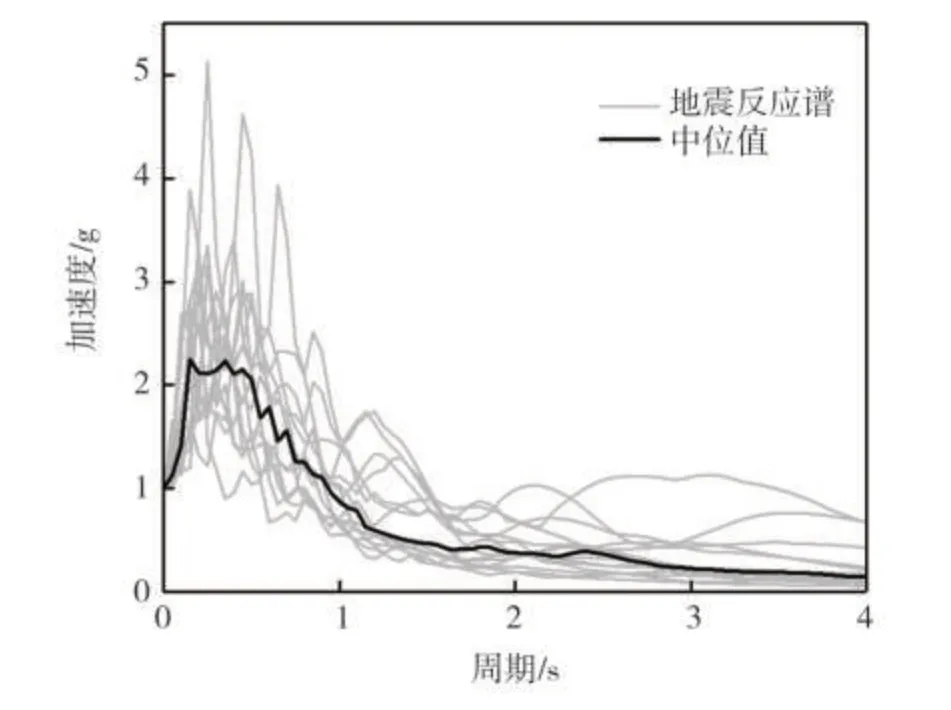
图5 地震记录加速度反应谱Fig.5 Acceleration response spectrum of seismic record

表4 层间位移角限值Table 4 Limitsof inter-story drift ratio
2.2 IDA分析结果
计算得到的IDA 曲线如图6 所示。从框架KJ1、KJ2 和KJ3 的IDA 曲线可以看出:主震PGA 由0.4 g 调幅到0.7 g 和1.0 g 过程中,可以看到愈发明显的初始位移角,说明主震后的残余位移有所增加。同时IDA 曲线的离散程度明显增大,究其原因,主要包括结构自身特性的内因和地震波差异的外因。随着地震(主震)强度增加,结构的初始破坏程度提高,非线性程度加深,地震响应的不确定性增大,使IDA 结果呈现出明显的离散性。此外,不同主震和主余震序列在周期、持时、速度、加速度等方面存在差异,随着地震强度的增加,地震波的自身特性逐渐凸显,不同的结构响应不断放大,计算结果的离散型程度也随之增大。对比KJ1、KJ2和KJ3三榀框架的IDA曲线,其变化趋势相近,地震反应趋同,说明配置HRB400、HRB500和HRB600钢筋的框架结构有类似的受力和破坏机理。
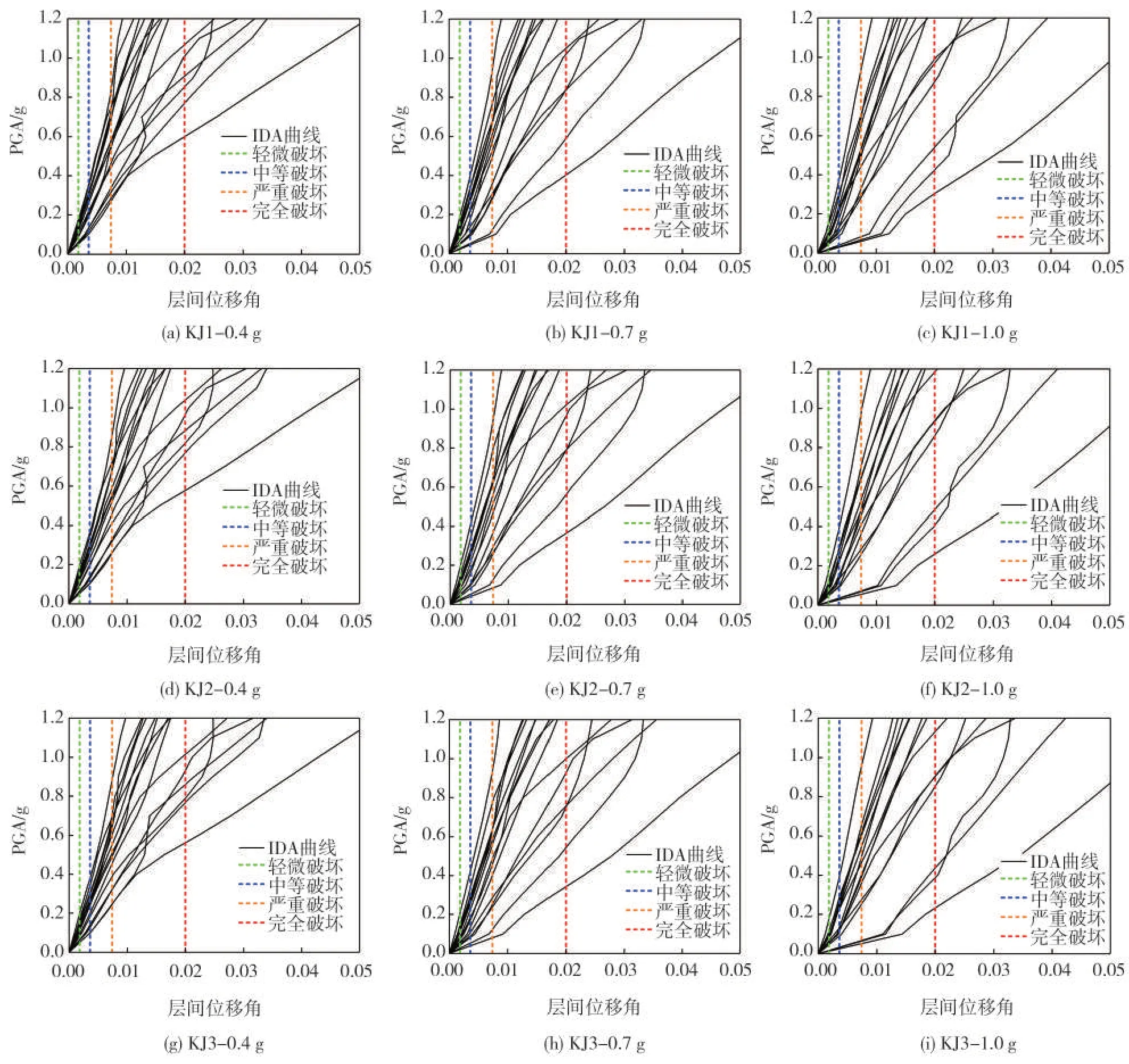
图6 IDA结果Fig.6 Results of the IDA analysis
2.1 节中划分的四个破坏状态能反应地震的损伤程度。对比同一榀框架的IDA曲线,可以看到提高主震强度后,余震作用的最大层间位移角到达某一极限状态限值时的地震强度需求(PGA)明显降低,同时,余震作用的初始位移角显著增加,说明主震对结构的损伤作用明显并产生残余变形,且对余震下的结构响应有放大作用。
3 地震易损性分析
3.1 易损性计算
地震易损性分析主要通过绘制易损性曲线预测结构发生各级破坏的概率。易损性曲线表示结构在某一地震动强度IM下结构需求EDP(Engineering Demand Parameter)超越结构能力C的条件概率[13]。结构需求EDP即结构的地震响应DM。
一般认为,结构需求DM与地震动强度IM的关系如下:

左右取对数,可知两者之间存在对数线性关系:
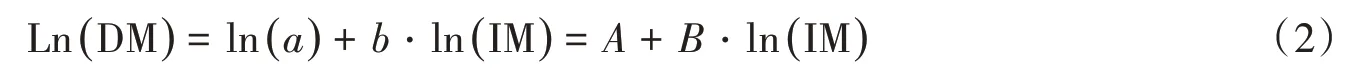
式(2)即概率地震需求模型,参数a、b(或A、B)可以由IDA数据的线性回归求得。以图6(a)数据为例,对其进行线性回归,结果见图7。
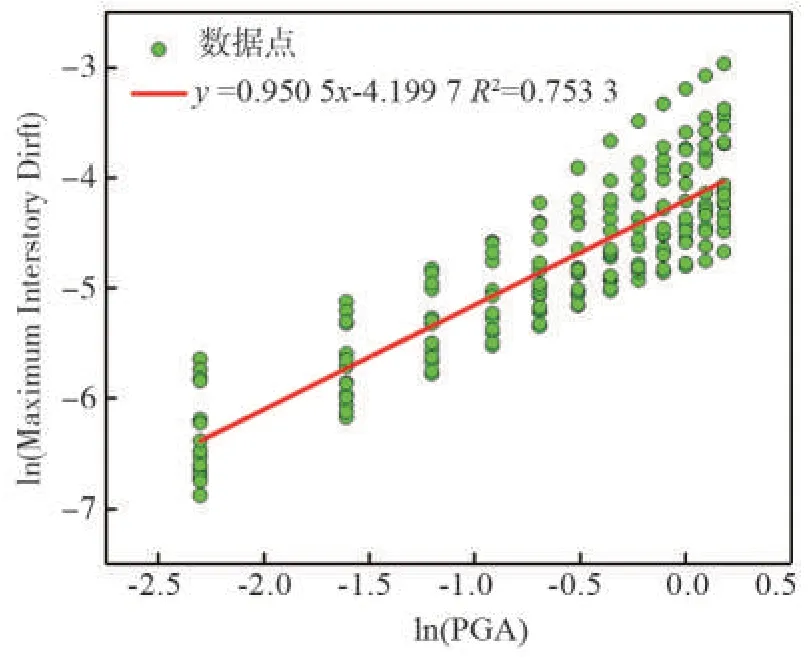
图7 KJ1-0.4 g线性回归Fig.7 Linear regressionofKJ1-0.4 g
假定地震易损性函数的计算模型为DM与IM的对数正态分布函数,则有:
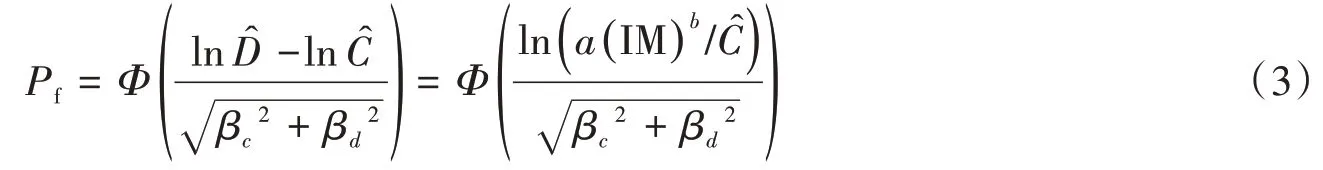
3.2 地震易损性曲线
图8为框架KJ1、KJ2和KJ3在0.4 g、0.7 g及1.0 g三个不同主震PGA下的主余震易损性曲线,以及单独主震作用下的易损性曲线。对比同一框架不同主震强度的易损性曲线,可知主震强度越大,结构到达各极限状态的概率均有不同程度的增加,以图8(a)为例,主震PGA为0.4 g时,框架KJ1达到严重破坏状态的概率为37.1%,主震PGA 增加到0.7 g 和1.0 g 时,严重破坏的概率分别为47.5%和57.9%。分别提高了28.4%和56.5%,说明主震强度的提高大幅度地增加余震的破坏风险。同时,单独主震下的易损性曲线均位于各极限状态曲线的最下方,说明余震使结构更易遭受破坏。由KJ2和KJ3的易损性曲线亦可以得到相同的结论。
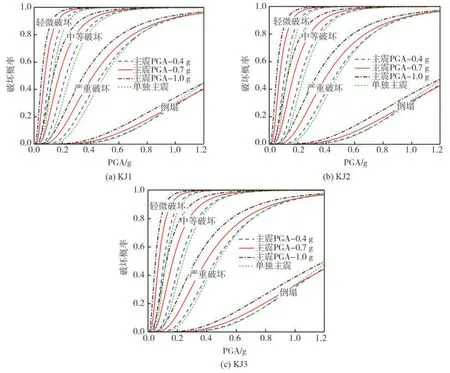
图8 不同主震强度的易损性曲线对比Fig.8 Contrast between vulnerability curves in different mainshock intensities
图9 为KJ1、KJ2 和KJ3 三榀框架易损性曲线的对比。可以看到三榀框架的易损性曲线趋于一致,仅对倒塌破坏概率的影响较大,其他破坏状态的差异并不明显。余震调幅至1.2 g 时,KJ2 和KJ3 倒塌概率较KJ1分别增加了约5.8%和10.7%,说明等强代换原则下,随着钢筋强度的提高,结构受力构件的配筋减少,对主余震作用下结构的倒塌性能存在一定程度的不利影响,但影响有限。
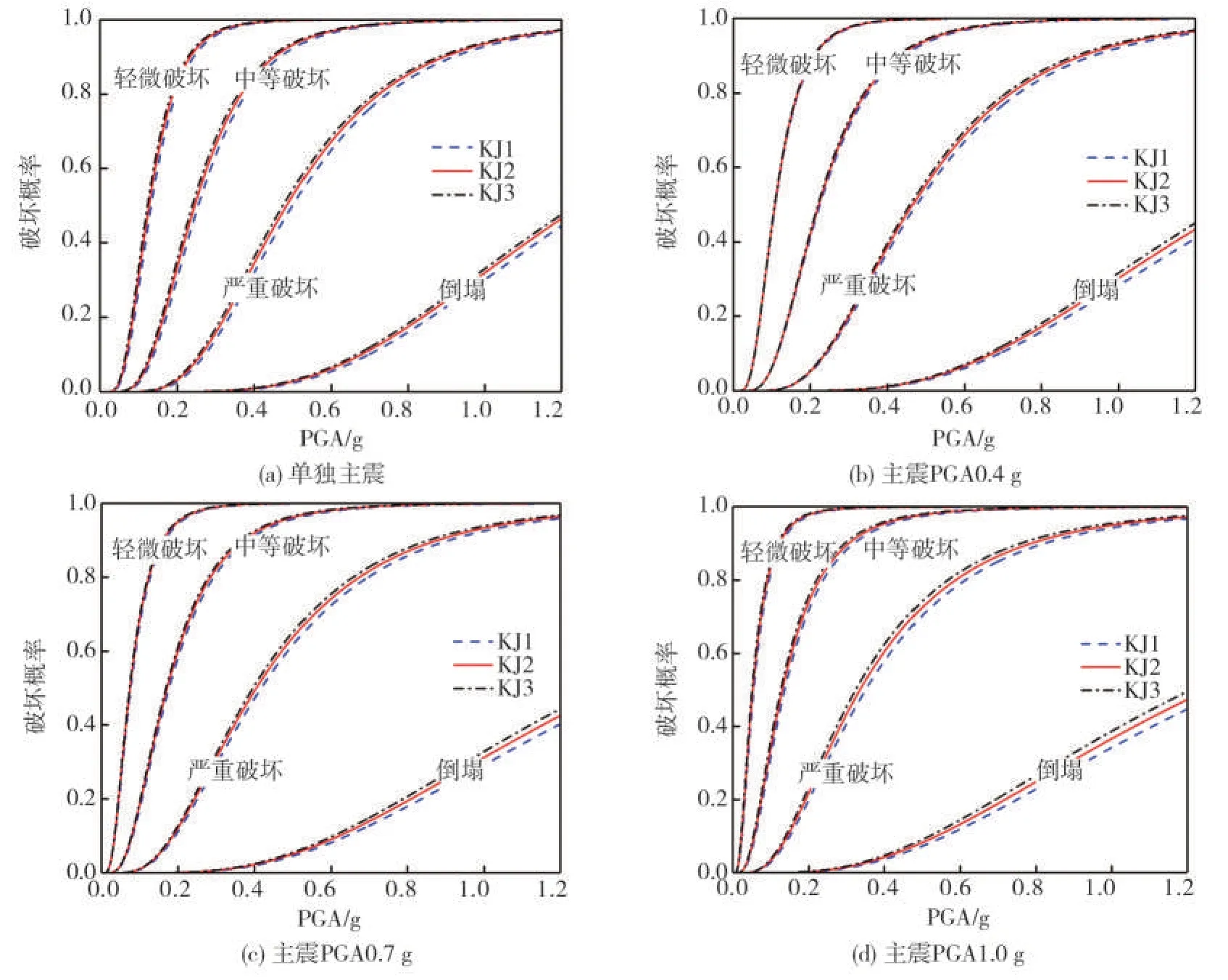
图9 KJ1、KJ2和KJ3易损性曲线对比Fig.9 Contrast between vulnerability curves of KJ1、KJ2and KJ3
4 结论
对15条地震加速度时程进行调幅并构造主余震序列,对三榀高强钢筋混凝土框架结构进行增量动力分析,研究了钢筋强度等级与主震强度对框架主余震易损性的影响,得到结论如下:
(1)由IDA分析可知:随着主震强度(PGA)的增加,高强钢筋混凝土框架结构的主震损伤更加明显,产生了更大的残余层间位移角,余震作用的最大层间位移角有所增加,IDA曲线也呈现出更大的离散性。
(2)易损性分析的结果表明:主震强度对主余震作用下高强钢筋混凝土框架结构的破坏概率有重要影响,主震强度的增加,使高强钢筋混凝土框架结构发生各级破坏的概率明显提高,增大了余震下该结构的破坏风险。
(3)KJ1、KJ2和KJ3三榀框架均可得到以上结论,说明配置HRB400、HRB500和HRB600钢筋的RC 混凝土框架结构在主余震作用下的地震表现存在相似性。但“等强代换”时,钢筋强度等级的提高将对结构抗倒塌性能产生不利影响,但影响程度有限。
