石材幕墙结构抗震性能试验研究

陈 盈，许乃鑫，张文学，刘叶锋

（1.北京工业大学建筑工程学院，北京 100124；2.中国建筑装饰集团有限公司，北京 100037）

引言

石材幕墙有着庄重大方和美观耐用的特点，在高档幕墙装饰工程中被广泛采用［1］。作为一种建筑围护结构，石材幕墙属于脆性材料，当地震发生时，石材在高空坠落会导致财物损失和人员伤亡［2］。石材幕墙多采用干挂法，利用金属挂件将其固定于建筑主体结构上。金属挂件在地震过程中的响应十分复杂，导致石材的边界条件难以确定，一般理论简化计算很难模拟石材真实的地震响应，因此模拟振动台试验是直接检验石材幕墙抗震性能最有效的手段。相较于玻璃幕墙的应用与研究［3－4］，目前对石材幕墙结构的研究尚不完善。胡晓等［5］结合实际工程，进行了石材幕墙结构的振动台试验，检验了石材幕墙良好的抗震性能，但忽略了支架与石材及支撑结构的动力耦合影响；徐忠根等［6］通过振动台试验，对比五种石材幕墙连接方式，发现采用可拆装挂钩式连接方式的石材幕墙抗震性能最优；王明贵等［7］定性地研究了背栓式连接石材幕墙的抗震性能，振动台试验表明栓接节点在大震下开始滑动，石材板块易发生碰撞与滑移；黄小坤等［8］进行了陶板幕墙的振动台试验，发现钢框架构件存在局部振动，在幕墙设计时应引起注意；卢文胜等［9］总结以往振动台试验的经验，建议以加速度响应和位移响应为抗震性能指标来判断幕墙抗震性能。

以上石材幕墙的振动台试验多为缩尺试验，缺少关于石材幕墙足尺试验地震响应特性和破坏特征的完整分析。因此本文就阿尔及利亚大清真寺南区石材幕墙体系进行振动台模型试验，研究了El Centro 波和两条场地人工波作用下该体系的抗震性能和破坏特征。并在此基础上，建立石材幕墙体系自振频率的简化计算模型，为石材幕墙抗震性能分析提供可靠的参考。

1 试验概况

1.1 试验模型

采用3 m×3 m 地震模拟振动台系统进行加载，参考相关规范［10－15］，对石材幕墙结构进行振动台试验，试验模型如图1所示。采用钢结构支架模拟实际主体结构，为石材幕墙提供支承，并传递地震作用。钢框架和石材的连接采用销钉连接。将支架通过10.9 级M30 螺栓固定于地震模拟振动台台面上。钢架立面尺寸及挂件连接节点如图2-图3所示。

图1 振动台试验模型Fig.1 Structural model on shaking table

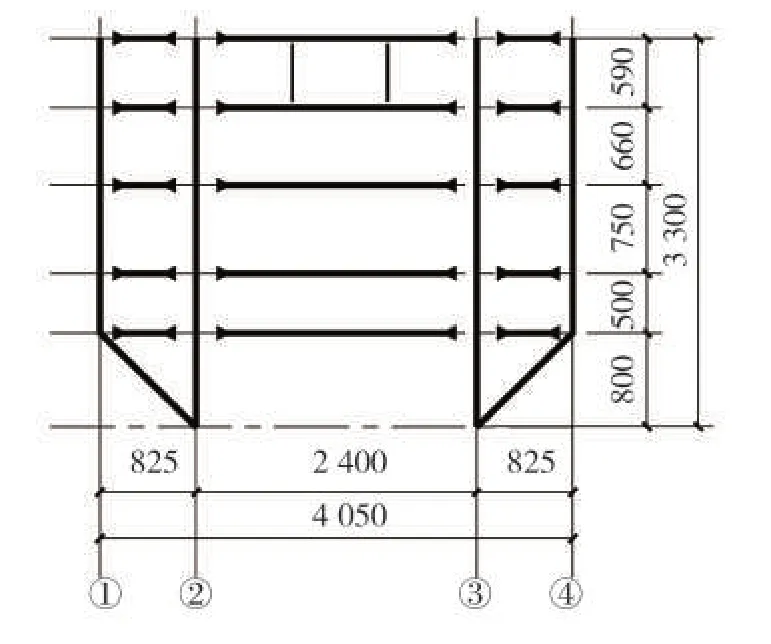
图2 钢架立面尺寸图（单位：mm）Fig.2 Steel frame elevation size

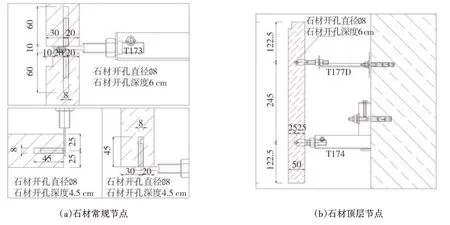
图3 挂件连接节点图Fig.3 Connection node

1.2 测点布置

定义石材幕墙平面的水平方向和竖直方向分别为X轴和Z轴，垂直于石材幕墙平面方向为Y轴。如图4（a）所示，每层钢架布置两个加速度传感器，用于测量钢架X 向和Y 向加速度响应，共计10 个；钢架X 向和Y向分别布设拉线式动态位移计各1个。如图4（b）所示，石材幕墙从下至上第一层、第二层和第四层每层布置两个加速度传感器，用于测量石材X向和Y向加速度响应。第三层石材幕墙加速度响应较大，因此在第三层上部和下部分别布置两个加速度传感器。同时，在石材幕墙第二至第四层沿对角线布置应变片共计18 个，用于测量石材X 向和Z 向的应变响应。在每层石材挂件上沿挂件轴线方向（Y 向）设置应变片，用于测量挂件的应变响应。另外在台面沿X向和Y向分别布置加速度传感器用以记录台面波。

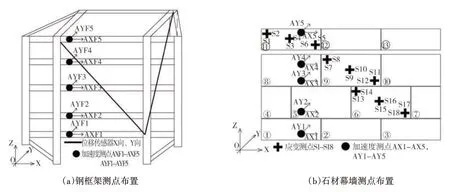
图4 模型测点布置Fig.4 Measuring points arrangement of model

1.3 试验工况

试验包括两组模型，其尺寸、材料与连接方式完全相同，仅加载工况不同。根据实际建筑场地特点，选取El Centro 波、人工地震波EQ3 和EQ4 作为输入，检测体系的抗震能力，三种波形如图5 所示。人工地震波EQ3和EQ4与阿尔及利亚规范PRA99-2003的设计反应谱对比如图6所示［16］。

图5 地震波加速度时程曲线Fig.5 Time history curves of acceleration

图6 地震动反应谱Fig.6 Earthquake Response Spectrum

试验加载工况见表1，按照加速度峰值（PGA）从0.1 g 开始以0.1 g 为增量的方式逐级加载，每级加载时三条地震波按照El Centro 波、EQ3 波和EQ4 波的顺序依次进行。在每个工况加载前后，均进行白噪声试验以确定模型的自振频率。对于模型1，先沿X 向按照PGA 从0.1 g 至0.6 g 逐级加载，之后继续进行Y 向PGA从0.1 g 至1.5 g、1.7 g 逐级加载，再继续进行X 方向PGA 从0.7 g 至1.5 g 逐级加载。对于模型2，先进行Y 向PGA 从0.1 g至1.0 g逐级加载，之后继续进行X 向PGA 从0.1g至1.0g逐级加载，再继续进行Y 向PGA 从1.1 g至1.7 g逐级加载，最后继续进行X向PGA从1.1 g至1.5 g逐级加载。模型1没有进行Y方向PGA=1.6 g工况的加载，直接进行了PGA=1.7 g的破坏加载。

表1 试验加载方案Table 1 Test loading program

2 试验现象

在所加地震作用下，两组模型均未出现严重的破坏情况，且损伤现象基本相似。以模型2 为例，加载Y向加速度峰值为0.4 g 的地震波后，结构整体完整，幕墙石材在销钉连接处开始轻微破损，如图7（a）所示；加载X 向加速度峰值为0.6 g 的地震波后，挂件与石材连接处的螺栓开始出现松动现象，各销钉处石材背面面积破损略有增大，石材局部掉落，暴露出销钉，如图7（b）所示；在X向加速度峰值为1.5 g的地震波作用下，模型整体性依然良好，如图7（c）所示。但石材在平面内摇晃明显，且出现跳动现象，石材已有破损进一步发展，振动过程中有少量细小碎块掉落，螺栓松动情况明显，如图7（d）所示。

图7 模型损伤情况Fig.7 damages of model

3 结构响应结果及分析

3.1 自振特性

由模型顶部加速度响应进行功率谱分析得到各级地震波输入前后模型自振频率变化如图8 所示。可见：随着输入加速度峰值逐级增加，两个模型的两个方向基频都呈现下降趋势。输入加速度峰值超过1.0 g的地震波后，基频下降程度更加明显，直至最后加载结束，模型1 和模型2 的X 向基频分别降低了15.57%和29.27%。试验过程中主体钢结构无明显损伤，因此结构自振频率降低程度不大。模型1 的Y 向基频在整个加载过程中变化不大，但在输入加速度峰值为0.8 g和0.9 g的地震波后，挂件松动引起石材产生滑移导致其边界条件突变，Y 向基频突然降低。同样由于挂件累积松动，模型2在输入加速度峰值为1.1 g的地震波后Y向基频突然降低。

图8 自振频率变化曲线Fig.8 Variation curves of natural frequency

钢架按照弹性理论设计，其在整个加载阶段未发现明显的变形，因此连接件的松动是基频降低的主要原因，而挂件安装质量和石材的差异导致两个模型测试结果略有不同。

3.2 加速度响应

实际工程要求幕墙结构设防烈度为8 度罕遇，主体结构最大加速度峰值响应应达到1.7 g。根据对高层建筑模型试验成果的分析和现行规范的规定［9－10］，将幕墙最大加速度峰值响应与规范规定的地震地面加速度峰值的5倍（表2）进行比较，判断其是否达到设防烈度要求。

表2 抗震设防烈度下加速度峰值响应Table 2 Peak value of acceleration response under seismic precautionary intensity

选择钢架顶部测点AXF4、AXF5和石材顶部测点AX4、AX5的加速度峰值响应进行分析。模型2加速度峰值响应变化如图9所示，对应输入加速度峰值为0.2 g、0.4 g、0.6 g和0.8 g地震波时钢架及石材的加速度放大系数如图10所示。由图9-图10可知：

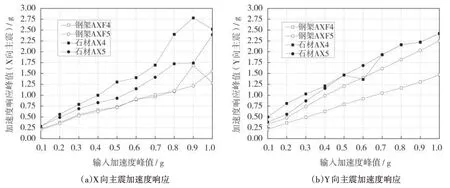
图9 加速度峰值响应曲线Fig.9 Acceleration response peak curve

图10 加速度放大系数Fig.10 Amplification coefficient of acceleration

（1）在台面输入加速度峰值为0.8 g的地震波时，钢架达到了实际工程要求的1.7 g加速度峰值响应的标准，同时石材的加速度峰值响应也达到了8度罕遇地震下幕墙加速度峰值不小于2.0 g的标准。此时结构性能良好，仍可继续承载，其抗震性能满足设防烈度要求。

（2）X 向主震时，当台面输入加速度峰值从0.1 g 提高至0.4 g，结构的加速度峰值响应线性增加，此时挂件无明显损伤；台面输入加速度峰值从0.5 g提高至0.7 g时，挂件轻微松动，石材与钢架的加速度峰值响应曲线发生波动；台面输入加速度峰值高于0.8 g时，挂件X向损伤变形明显，此时石材与钢架的加速度峰值响应出现明显波动。Y向主震时，石材与钢架的加速度峰值响应基本成线性变化，说明挂件轴向（Y向）连接可靠度高。

（3）X 向主震时，由于钢架第四和第五层有附加竖向角钢连接，因此钢架四层和五层测点的加速度峰值响应趋于一致。石材顶层挂件连接方式与其余层不同，因此石材测点的加速度峰值响应在顶层处明显增大，说明连接挂件规格与连接位置对石材加速度响应影响较大，因此石材幕墙的边界条件是影响幕墙地震响应的关键因素。

（4）石材测点的加速度放大系数整体大于同位置处钢架测点的加速度放大系数，说明挂件与石材之间存在间隙，发生碰撞导致石材加速度响应增大；且X向主震时，放大效应更明显。

（5）X 向主震时，石材的加速度放大系数随测点层数的升高成先增大再减小的趋势，说明挂件连接规格对X 向石材加速度放大系数影响较大。Y 向主震时，石材的加速度放大系数随测点层数的升高成线性增加变化，进一步说明了挂件轴向（Y向）连接的可靠度高。

（6）在台面输入加速度峰值为0.8 g 时，不仅挂件松动明显，而且发生了变形；此时石材的加速度放大系数存在低于其它加载工况的现象，说明挂件的松动和变形缓冲了石材和钢架的碰撞，降低了石材面板的加速度响应。

3.3 位移响应

在水平地震荷载作用下，主体钢架发生侧移，在人工波EQ4作用下钢架的侧移量最大，各级地震作用下模型1 的层间位移角峰值如图11 所示。可见：随着台面输入加速度峰值的增加，X 方向和Y方向的层间位移角均线性增加。Y 方向钢架的斜撑有效地提高了结构在该方向上的抗侧刚度，X 方向主震的层间位移角约为Y方向主震的2倍。

图11 模型层间位移角Fig.11 Floor displacement angle of model structure

3.4 应变响应

表3为模型2部分工况下石材以及挂件的最大应变值。可见：随着台面输入加速度峰值的增大，石材各测点处应变略有增加。在试验过程中，模型中部的加速度响应较其他部位更加剧烈，因此该部位的石材面板应变响应较其他位置也更加明显。整个加载过程中，石材的X向应变普遍较低，当输入地震波峰值达1.3 g时，X向最大应变仅有89.72 μm/m。当输入地震波峰值达1.4 g时，虽然Z方向应变最大为853.30 μm/m，小于石材的极限应变值1 000 μm/m，但明显大于X方向应变，因此在实际工程中石材应在Z方向采取可靠的连接措施。

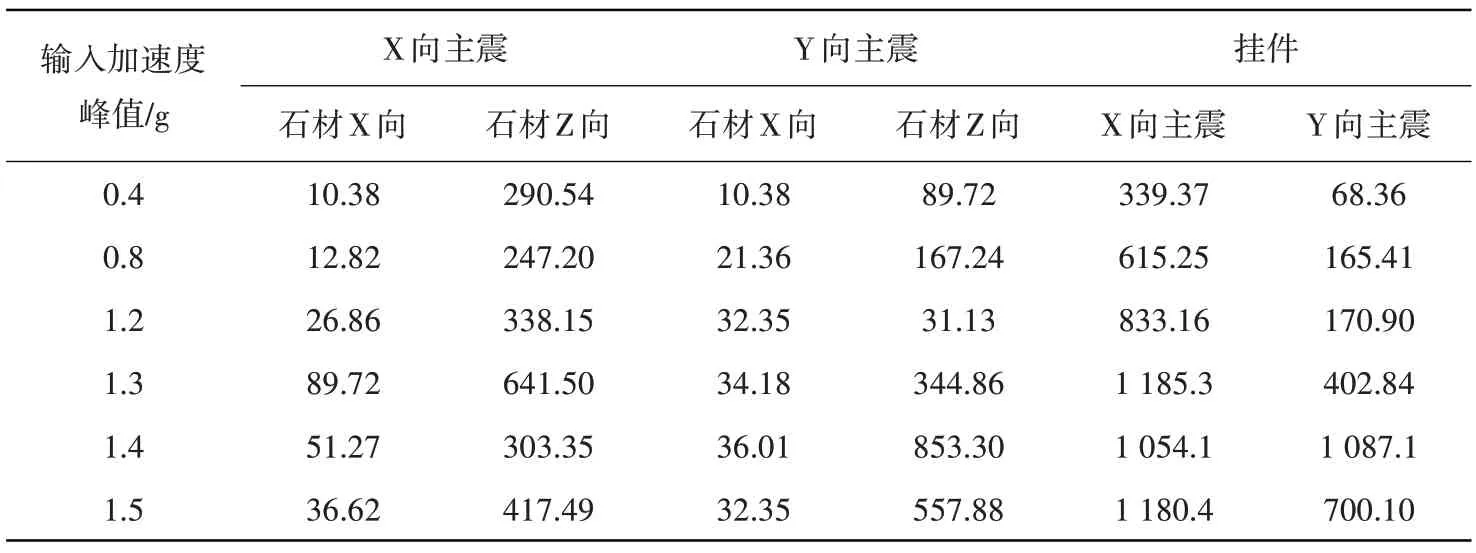
表3 最大应变值（μm/m）Table 3 Maximum strain value（μm/m）

挂件采用AISI316L不锈钢，最大弹性应变为917 μm/m，试验中挂件最大拉应变为1 185.34 μm/m。说明地震过程中挂件产生了较大的变形，缓冲了地震作用。

4 石材幕墙结构自振频率简化分析模型

4.1 模型假定

若考虑钢架与石材及挂件连接结构的动力耦合作用，整体结构的刚度矩阵较为复杂，在简化计算模型中，用钢架的刚度矩阵代替整体结构的刚度矩阵，将石材和钢架的质量均集中在每层对应位置，得到如图12所示的简化串联质量模型，其中：mi表示第i层的等效质量；ki表示第i层钢架的抗侧移刚度；i=1～5。

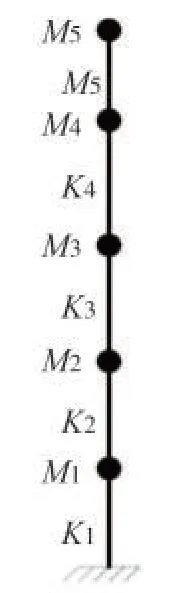
图12 简化计算模型Fig.12 Simplified model

忽略阻尼，建立多自由度体系自由振动运动方程［17］：

式中：［M］=diag（m1，m2，m3，m4，m5）为质量矩阵，{u}为各层的侧向位移向量，刚度矩阵为：

进一步可得到体系的频率方程［17］：

4.2 未震损模型

选择模型1的X向一阶自振频率进行模型验证。将质量矩阵和刚度矩阵分别代入频率方程（式2），可得到结构X向的五阶频率如下。

ω’=(8.3 73.4 137.7 224.0 233.3)T

其中：质量矩阵为［M］=diag（408，600，658，429，432）kg，刚度矩阵为：

由简化模型计算得到的X 向基频为8.3 Hz，与试验实测值8.35 相比误差仅0.06%，可见该简化模型可以很好的预测未损伤结构的自振频率。

4.3 震损结构模型

随着地震动加速度峰值的增加，挂件连接逐渐松动，结构的实际整体刚度减小，简化模型中刚度矩阵保持不变，引入质量修正系数{β}对结构质量矩阵进行修正。质量修正系数和修正后结构每层质量按式（3）和式（4）计算，当βi＜0时取βi=0。修正后的质量矩阵为［M1］，频率方程如式（5）。

式中：Fi为最大响应力，由每层加速度峰值响应与每层质量相乘可得；Fgi为结构加速度峰值响应为1 g时各层的响应力；mi’为修正后的每层质量。

由试验可得在台面输入加速度峰值为0.4 g和0.8 g时，每层钢架和石材面板的加速度峰值响应。分别取钢架和石材测点的加速度峰值响应计算质量修正系数和修正质量，见表4。

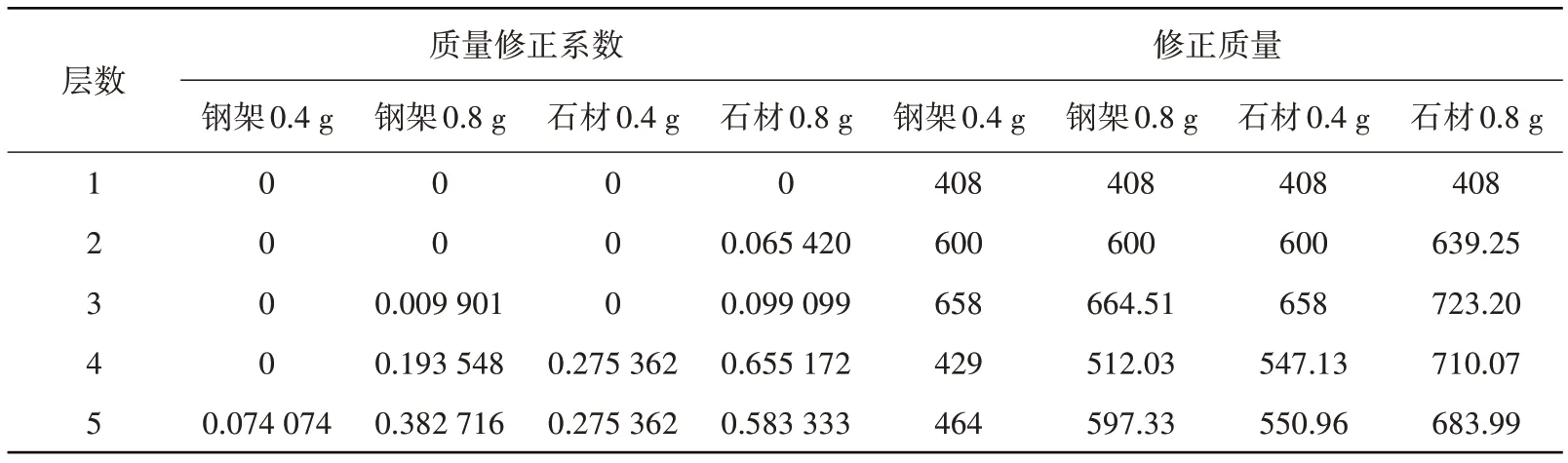
表4 质量修正系数（β）及修正质量m‘（kg）Table 4 Quality correction factor and corrected quality

将修正后的质量矩阵代入频率方程（式5），可得震损结构的一阶自振频率见表5。

表5 震损结构自振频率ω（Hz）Table 5 Natural frequency of earthquake damaged structures

可见：当采用钢架测点所得的质量修正系数时，默认石材与钢架刚性连接完好，未考虑挂件松动对自振频率的影响，因此钢架测点处计算的震损结构自振频率比试验值大；采用石材测点所得的质量修正系数时，由于连接件的松动引发的相对碰撞会二次放大结构加速度响应，导致质量修正系数偏大，计算的震损结构自振频率偏小。采用质量修正系数计算的震损结构自振频率最大误差为3.32%。钢架测点与石材测点计算的震损自振频率平均值与试验测得自振频率最大误差仅为1.31%。

由此可见：当干挂石材结构在地震作用下出现连接挂件松动时，通过附加虚拟质量的方法可以较好的表现连接挂件松动导致的结构自振频率的变化。

5 结论

通过对干挂石材幕墙结构的振动台试验和结构自振频率简化模型的研究，主要得出以下结论：

（1）依托阿尔及利亚大清真寺南区石材幕墙工程进行振动台试验，试验结果表明石材幕墙结构整体在8度罕遇地震作用下，仍未发生明显的结构破坏，石材幕墙结构整体抗震性能良好。

（2）模型X 向的抗侧刚度小于Y 向，因此其位移响应更加明显。石材刚度远大于挂件刚度，因此挂件的变形较大，且挂件对石材的地震响应起到了一定的缓冲作用。石材Z方向应变明显大于X方向应变，因此实际工程中建议挂件与石材Z方向之间采用可靠的连接方式。

（3）石材的加速度响应受挂件连接位置和规格影响较大，最大加速度响应并不一定出现在顶层。同一水平位置时由于挂件与石材之间的间隙引发的碰撞效应，石材的加速度响应明显比主体结构大。

（4）挂件轴向（Y 向）连接可靠度高，结构加速度响应基本成线性变化，而挂件X 向连接损伤对石材与钢架的加速度响应影响较大，设计时应加强挂件X向连接的可靠度。

（5）在罕遇地震作用下，石材幕墙结构的震害以挂件松动为主，而挂件的松动有利于降低石材的地震响应。干挂石材体系的自振频率在逐级加载后略有下降，在简化串联质点模型中引入本文提到的质量修正系数可以较好的反映石材幕墙结构连接件损伤导致结构自振频率下降的现象。