基于增量动力分析方法的砌体结构地震易损性分析

2022-02-19熊立红官志刚吴善香

世界地震工程 2022年1期

熊立红，官志刚，吴善香

（中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，哈尔滨 150080）

引言

砌体结构具有取材方便、构造简单、施工容易、造价低廉和耐久性好等优势在我国被广泛应用。由于脆性突出使得砌体结构在强震作用下破坏非常严重，因此，砌体结构的抗震能力评价研究具有重要的理论意义和工程价值。

结构地震易损性分析作为建筑物抗震性能评估的手段，能确定结构破坏程度与地震强度间的关系，对于结构地震安全性评定、灾害预测以及损失评估等均具有重要作用。数值计算方法在结构易损性分析中应用广泛，其是通过数值分析得到结构地震响应，再结合概率方法获得易损性，该方法可在震害资料缺乏情况下得到易损性。

本文基于增量动力分析（Incremental Dynamic Analysis，IDA）方法，研究砌体结构易损性的影响因素及多层砌体结构易损性。

1 基于增量动力分析（IDA）的砌体结构地震易损性分析

IDA 方法是基于性能的地震工程中用于确定结构在不同地震动强度作用下反应的一种方法［1］。该方法既可得出不同强度地震作用下结构性能参数变化，还能给出不同地震动输入下结构地震反应差异，该方法广泛应用于结构性能评估中。

基于IDA的地震易损性分析，因IDA方法可计算不同地震动强度作用下的结构反应，而地震易损性分析是计算在不同强度地震作用下结构达到或超过某种极限状态的条件概率，故可根据IDA 分析结果，再结合极限状态就可得到结构地震易损性。

1.1 结构抗力和极限状态

基于IDA 的地震易损性分析方法，要确定恰当的地震强度参数及描述结构破坏程度的物理指标。本文以加速度峰值作为地震输入强度指标，以楼层延伸系数也就是楼层最大变形与开裂变形之比作为结构抗力指标，延伸系数与地震作用、结构强度以及结构刚度等相关。张令心等［2］基于试验结果及砌体结构的大量震害，得出了不同极限状态下延伸系数承载力的中值uR以及对数标准差σR，见表1。轻微及中等破坏状态的延伸系数承载力可在初裂和严重破坏的延伸系数承载力之间插值求出，可取1/5点和3/5点的相应值。

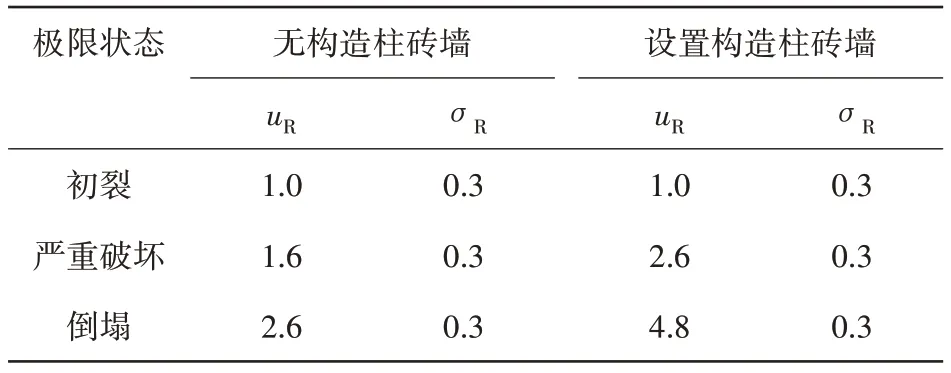
表1 延伸系数承载力Table 1 Coefficient of elongation and bearing capacity

1.2 砌体结构地震反应分析

1.2.1 砌体结构简化模型及恢复力模型

砌体结构非线性地震反应分析采用串联多自由度模型，其恢复力可按夏敬谦［3］提供的模型，如图1 所示。其中：Fy、Fu和Fp分别表示层间开裂、极限和倒塌破坏控制点荷载；Δy、Δu和Δp分别代表开裂、极限和倒塌破坏位移。对于砖砌体结构各控制点荷载可按式（1）-式（3）取值。

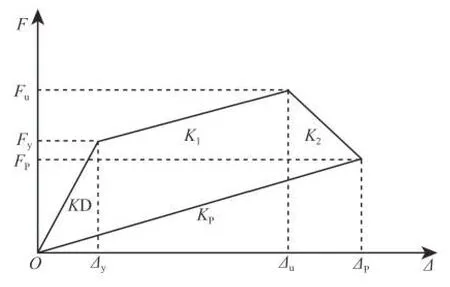
图1 砖砌体结构层恢复力模型Fig.1 Restoring force model for the masonry stucture

式中：ξ—砌体截面剪应力不均匀系数，矩形截面取1.2；fmv—砖砌体沿通缝抗剪强度平均值；A—承受地震力的层间墙体横截面面积总和；σ0—作用在墙体上的平均压应力。

砖砌体结构各控制点层间剪切位移角见表2。

表2 砖砌体结构各控制点层间剪切位移角Table 2 Inter-Laminar shears displacement angle of control points of brick masonry structure

参照我国房屋震害等级划分，可以给出砌体结构骨架曲线与破坏等级之间的对应关系如图2所示。

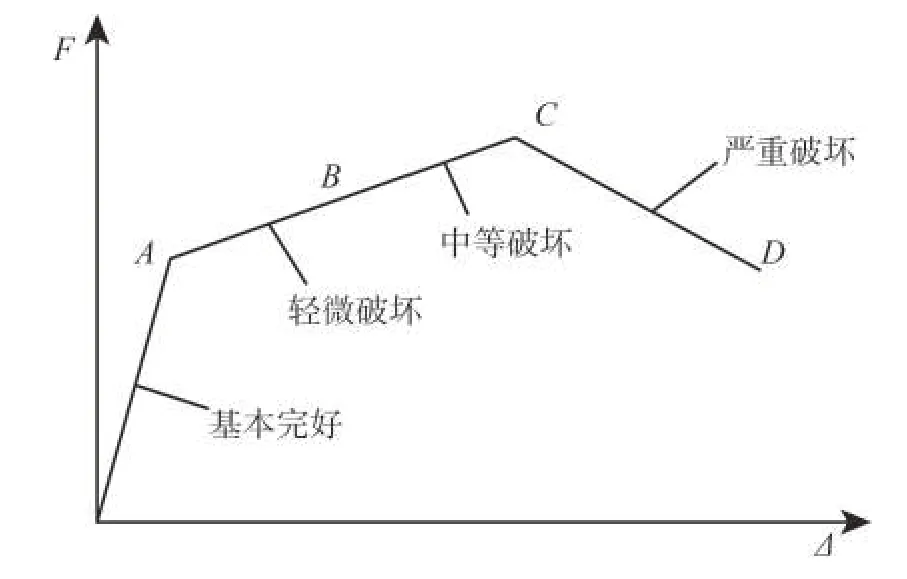
图2 骨架曲线与破坏等级对应关系Fig.2 Relationship between skeleton curve and damage levels

1.2.2 地震动的选择

地震动的不确定性是结构地震响应不确定性的最主要原因［4］。LUCO 等［5］研究表明：输入20 条地震动可较理想地反映地震动的不确定性，且分析结果具有统计意义。《FEMA·2008》（ATC-63）［7］主张分析地震易损性时采用多于20 条地震记录，以考虑地面运动不确定性带来的影响。本文针对II 类场地选取22 条地震记录用于砌体结构的IDA分析，所选地震记录的基本信息详见表3。

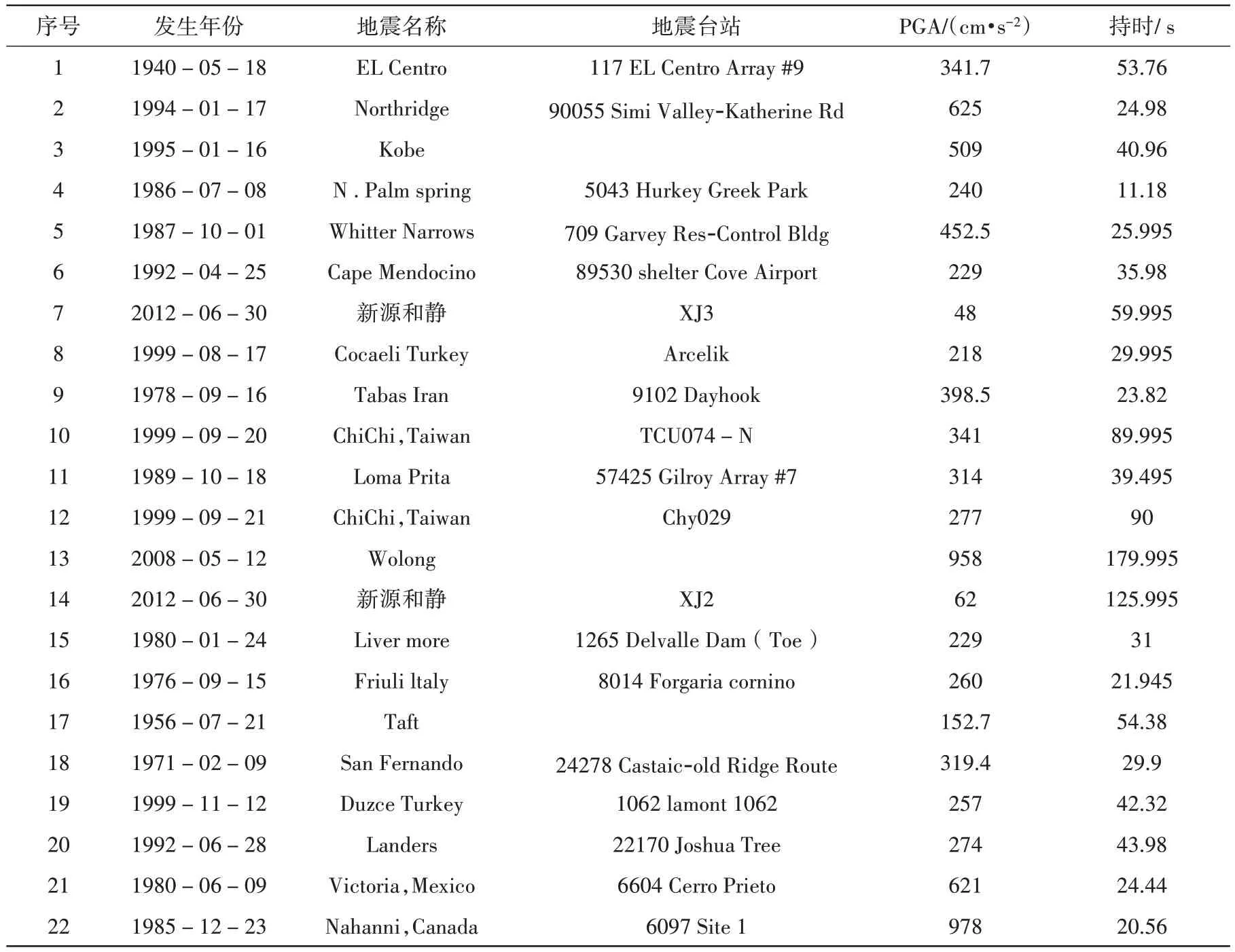
表3 所选地震动的基本信息。Table 3 Essential information of selected earthquakes

1.3 砌体结构地震易损性

根据张令心等［2］的研究结果，结构的最大延伸系数反应服从对数正态分布，故将时程分析所得最大延伸系数经统计分析，可得出对数正态分布函数的参数。在确定强度地震作用下，对应于某一极限状态的结构地震易损性可由该强度地震作用下结构承载力反应E。超过该极限状态对应的结构承载力R的概率Pf表述，如式（4）。

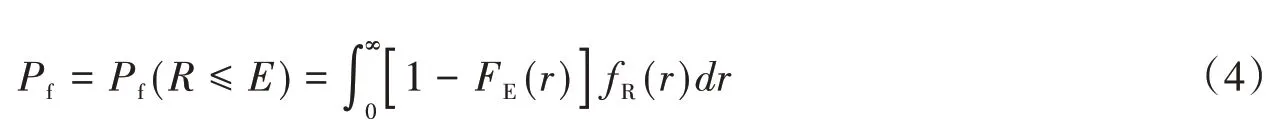
确定结构的承载力R及反应E的概率分布，便可由式（4）得到结构超过各破坏等级极限状态的概率。当结构的承载力和最大反应都服从对数正态分布时，式（4）可由式（5）来表示。

式中：uR、uE、σR和σE分别为结构承载力及最大延伸系数反应的中值和对数标准差。

对结构楼层最大延伸系数中值和地震动峰值加速度PGA 分别取对数，发现二者基本呈线性关系，假定二者关系可用式（6）表达。

则结构各破坏等级极限状态的超越概率可表示为PGA的函数：

式中：a和b分别为回归系数。由式（7）即可绘制结构地震易损性曲线。

2 砌体结构地震易损性的影响因素分析

为了研究不同因素对砌体结构地震易损性的影响［6］，以设防烈度为7 度与场地类别为Ⅱ类的典型多层砖砌体房屋为基本算例，输入了1.2.2 节选取的22 条地震动进行地震易损性分析。算例为普通烧结砌体房屋，采用混合砂浆砌筑，砖强度等级为MU10，墙体厚度为240 mm。算例平面如图3所示，所分析算例的平面布置相同，仅改变部分设计参数（层数、砂浆强度、层高、设防烈度和墙体面积率）的取值。

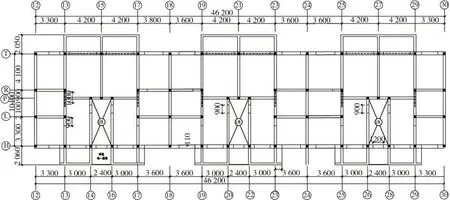
图3 算例平面图Fig.3 Structure-planofexamples

2.1 层数对砌体结构地震易损性的影响

对平面布置一致和层数分别为5 层、6 层以及7 层的3 栋砌体房屋进行IDA 及易损性分析。3 栋房屋层高相同，均为2.8 m，采用M10 混合砂浆砌筑而成。最大楼层延伸系数的平均IDA 曲线及易损性曲线分别如图4-5所示。

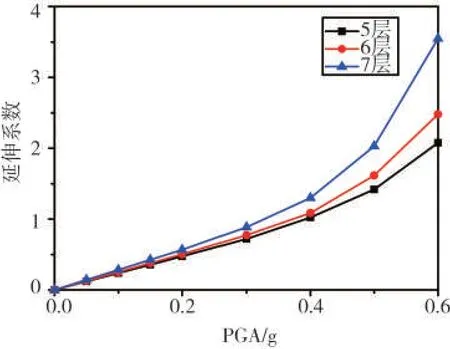
图4 不同层数砌体结构最大延伸系数平均IDA曲线Fig.4 Average IDA curves of different story masonry structures

由图4可见：结构层数越高，反应越大，且随着PGA的增加，不同层数结构的最大延伸系数反应的差别逐渐加大。

由图5可见：结构层数不同其地震易损性不同，5层和6层之间在同一PGA下，发生相同破坏程度的概率最大可相差8.56%；6层和7层间最大可相差14.98%；而5层和7层间最大可相差20.7%。

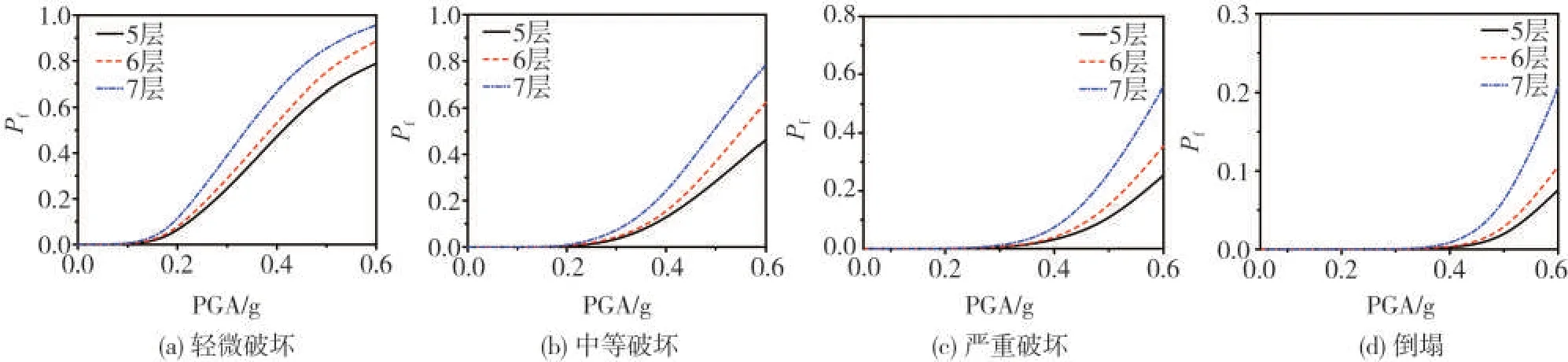
图5 不同层数砌体结构的易损性曲线Fig.5 Comparison of fragility curves of different story masonry structures

2.2 砂浆强度对砌体结构地震易损性的影响

对砌筑砂浆强度等级分别为M5、M7.5和M10的3栋5层砌体结构进行IDA 及易损性分析。结构层高均为3.0 m，结构最大楼层延伸系数的平均IDA曲线如图6所示以及易损性曲线如图7所示。

由图6可见：其他因素相同而采用的砌筑砂浆强度不同时，结构的最大楼层延伸系数反应与砌筑砂浆强度有关，砌筑砂浆强度越高，结构反应越小，且随着PGA 的增大，砂浆强度不同的结构反应差异愈大。当PGA＜0.2 g时，结构为弹性状态，结构反应随PGA 的增大而增加，不同的结构反应差别不明显；当PGA＞0.2之后，砌筑砂浆强度为M5的结构最早进入非线性，结构反应增长较快。

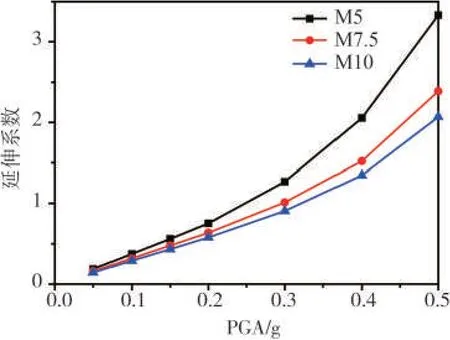
图6 不同砂浆强度砌体结构最大延伸系数平均IDA曲线Fig.6 Average IDA curves of masonry structures with different strength of mortar

由图7 可见：采用M5 和M7.5 的结构在同一PGA 下，发生同一破坏程度的概率最大相差18.52%；分别采用M7.5和M10的结构之间最大相差9.22%；而分别采用M5和M10的结构之间最大相差27.74%。由此可见：砌筑砂浆强度等级对砌体结构易损性的影响很大。

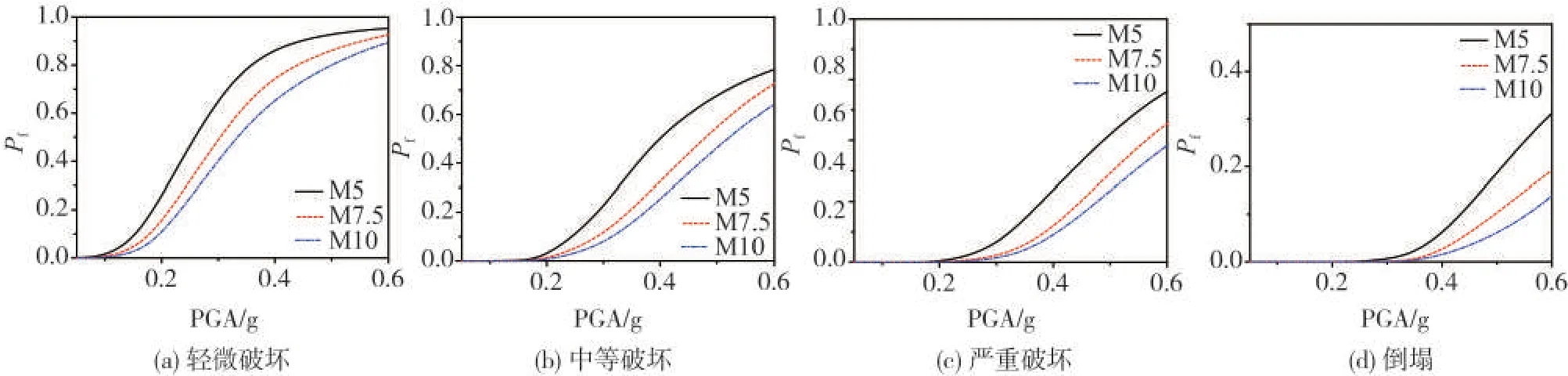
图7 不同砂浆强度砌体结构易损性曲线Fig.7 Comparison of fragility curves of masonry structures with different strength of mortar

2.3 层高对砌体结构地震易损性的影响

对层高分别为2.8 m、3.0 m 和3.3 m 的6 层砌体结构进行IDA 及易损性分析。三个结构砂浆强度均为M7.5，结构最大楼层延伸系数的平均IDA曲线如图8所示以及易损性曲线如图9所示。

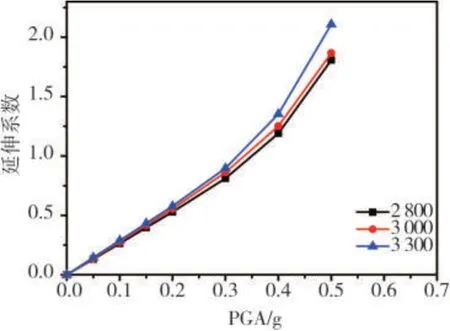
图8 不同层高砌体结构最大延伸系数平均IDA曲线Fig.8 Average IDA curves of structures with different floor heights

由图8可见：其他因素相同而层高不同时，层高越小，结构反应也小，但这种差别不大，特别是PGA＜0.4 g时，结构反应很相近。不同层高结构反应随PGA的增加变化不大。

由图9 可见：层高分别为2.8 m 和3.0 m 的结构，在同一PGA 下，发生相同破坏程度的概率最大相差6.33%；层高分别为3.0 m 和3.3 m 的结构间最大相差5.24%；而层高分别为2.8 m 和3.3 m 的结构间最大相差11.57%。可见层高在2.8～3.3 m之间的砌体结构，层高对其易损性的影响并不大。

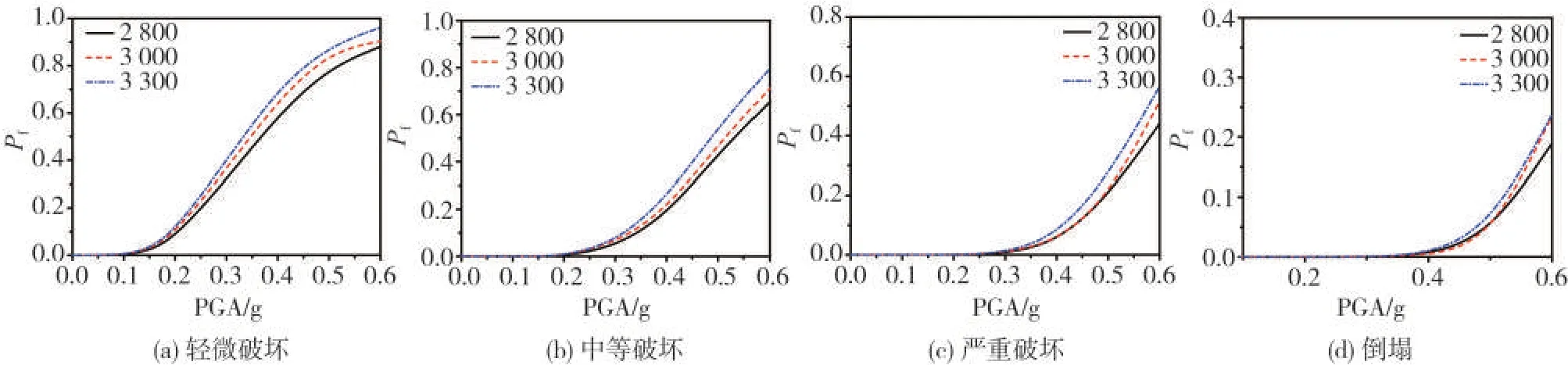
图9 不同层高砌体结构易损性曲线Fig.9 Comparison of fragility curves of structures with different floor heights

2.4 设防烈度对砌体结构地震易损性的影响

不同设防标准下砌体结构在抗震措施等方面要求不同。分别对6度、7度和8度设防的3栋5层砖砌体结构的进行易损性分析。结构层高均为3.0 m，砌筑砂浆强度M10。三个结构最大楼层延伸系数的平均IDA曲线如图10所示以及易损性曲线如图11所示。

由图10可以看出：设防烈度高的结构在相同PGA 作用下的反应越小。随着PGA 的加大，不同设防结构的反应差异也随之增加。

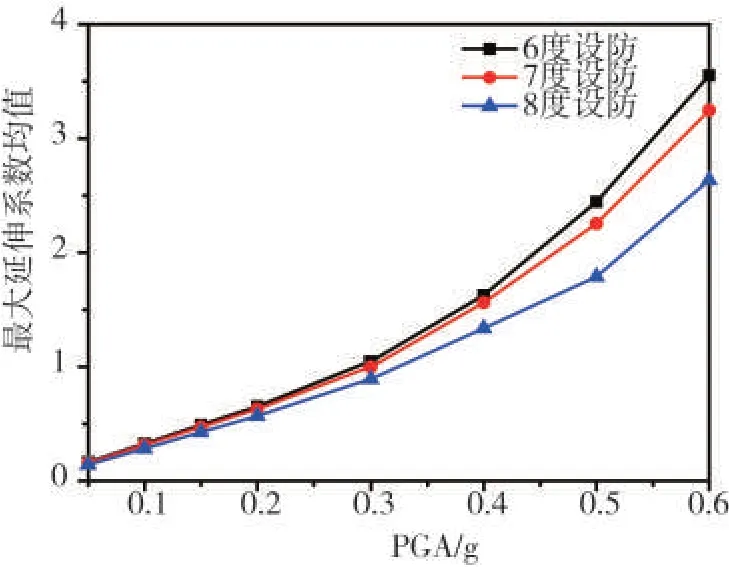
图10 不同设防烈度砌体结构最大延伸系数平均IDA曲线Fig.10 Average IDA curves of structures with different fortification intensity

由图11可见：6度与7度设防的结构发生相同破坏程度的概率差异不明显，而与8度设防结构间的差异较大。原因在于算例按6度和7度设防时布置的构造柱基本相同，而8度设防时布置构造柱明显多于6度和7度设防。

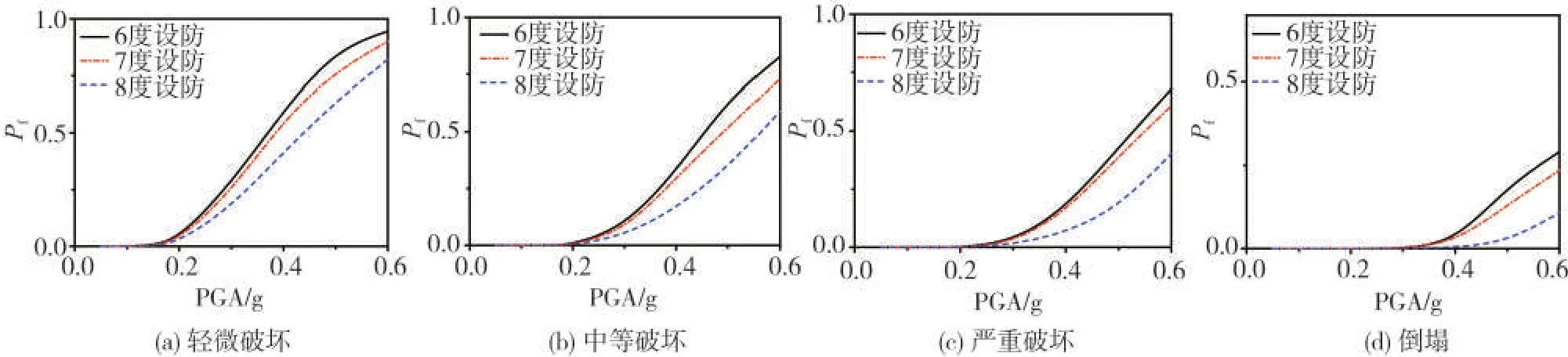
图11 不同设防砌体结构易损性曲线Fig.11 Comparison of fragility curves of structures with different fortification intensity

2.5 墙体面积率对砌体结构地震易损性的影响

砌体结构是以墙体为主要受力构件的结构，将地震作用方向的抗震墙总面积与楼层建筑面积之比定义为墙体面积率。为研究墙体面积率对多层砌体结构易损性的影响，分别对三个横向墙体面积率分别为7.15%、6.18%和5.26%（分别记为结构1、结构2 和结构3）的砌体结构进行易损性分析，易损性曲线如图12所示。

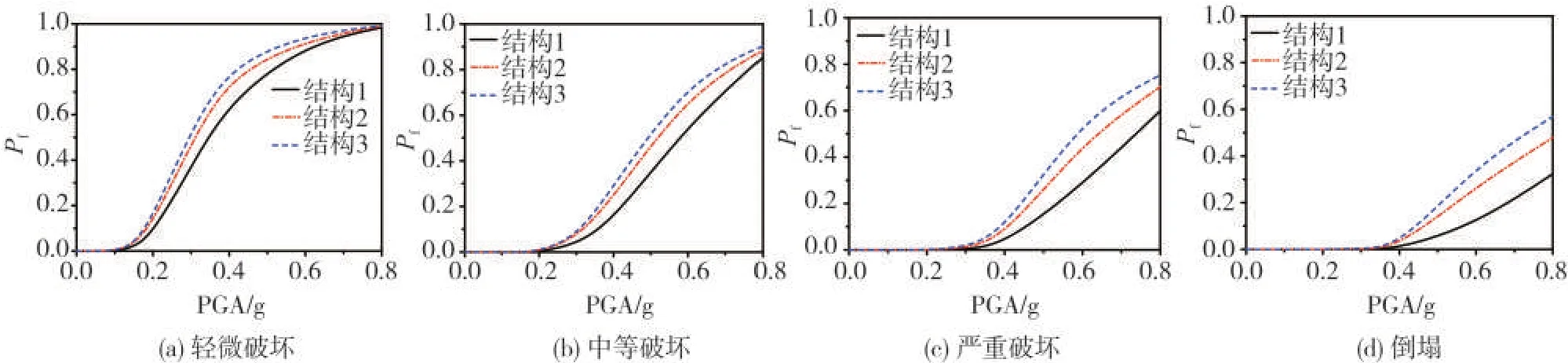
图12 不同墙体面积率砌体结构易损性曲线Fig.12 Comparison of fragility curves of structures with different wall area ratio

由图12可见：对于墙体面积率不同的结构，在同一PGA作用下发生某一破坏程度的概率是不同的，最大相差达16%。由此可见承受地震作用的抗震墙体面积直接影响结构的破坏程度。

3 不同度设防多层砌体结构群体易损性分析

张令心等［2］给出了借助于拉丁超立方采样技术和非线性时程分析的采用概率方法多层砖房地震易损性，该方法需建立一组代表性结构。按照建筑抗震设计规范（GB 50011-2010）［10］和《砌体结构设计规范》（GB 50003-2011）［11］分别设计了7 度和8 度设防的不同层数的多层砖砌体结构各9 栋，结构外墙墙厚370 mm，内墙墙厚240 mm，7度和8度设防砌体结构的区别仅在于它们的构造柱数量不同。此外，还设计了9栋未设防多层砌体结构，其平面布置与设防结构相同，只是未设置构造柱。限于篇幅，其平面布置图及设计参数省略。

分别对7 度和8 度设防及未设防多层砌体结构的易损性进行分析，得到结构的平均易损性曲线如图13所示。由图13 可知：在相同PGA 作用下，未设防、7 度设防以及8 度设防的结构发生同一破坏程度的概率依次降低。由图13（a）可见：结构轻微破坏时，尚未进入非线性，故三类结构的易损性曲线差别不大，表明此时构造柱与圈梁等构造措施尚未发挥作用。随着结构非线性的发展，易损性曲线差别越来越显著。尤其是倒塌状态，设防砌体结构发生倒塌的概率较未设防砌体小很多，表明砌体结构设置构造柱及圈梁能显著提高其抗倒塌能力。

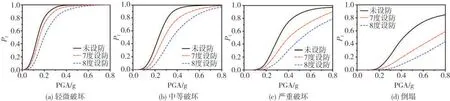
图13 不同设防多层砖砌体房屋的平均易损性曲线对比Fig.13 Comparison of fragility curves of multi-story masonry structures with different fortification intensity under respective damage levels